Z网络下新的推理算法在不确定决策中的应用①

张 最, 吴 涛,b,*, 涂成凤

(安徽大学a.数学科学学院;b.计算机智能与信号处理教育部重点实验室,安徽 合肥230039)

0 引 言

不确定决策是指充分考虑既有的不确定信息情况下,进行不确定性的推理,得到较为可靠的信息。对于不确定信息,Zadeh[1]于2011年提出了Z-number的概念,用来表示具有随机性和模糊性的不确定信息,但是不确定信息的推理较为复杂。针对这一问题,许多学者进行了研究,并且在处理不确定性过程中研发了很多不确定性推理技术,例如模糊推理、概率推理、Dempster-Shafer(DS)证据推理等等。模糊推理[2]是基于模糊集由不准确集得到不准确结论的过程;概率推理[3]是基于贝叶斯推理的不确定性推理方法,但这要依靠先验概率和条件概率;DS证据推理[4]是基于DS证据理论处理不能用概率表示只能用质量函数表示的“未知”信息。针对Z-number的不确定性推理,Jiang等[5]提出新的Z网络模型以及推理算法用来进行Z-valuation不确定性推理。基于Z网络模型,对Z-valuation不确定性推理过程进行一些改进,进而在决策过程中根据已知的信息进行改进后的推理,从而得到更加准确的信息,有利于决策人更好的进行决策。

1 基础知识

定义1[6]: (Z-number)Z-number是由有序的一对模糊数表示为Z=（A,R）,第一个元素是不确定变量的实值函数,是对X在值上的约束,第二个元素是对第一个元素可靠性的测度。

定义2[7]: (离散Z-number)离散Znumber是一个有序的离散模糊集对,记作X是（A,B）,其中A对随机变量X可能取的值进行模糊约束,它的隶属度函数为μA:｛x1,x2,…,x m｝→［0,1］,B为对A的概率测度的模糊限制,其隶属函数是μB:｛b1,b2,…,b n｝→［0,1］,b1,b2,…b n∈［0,1］,可写为P(X是A)=B。而有序三元组（X,A,B）被称为Zvaluation,或者说Z-valuation等价于赋值语句X是（A,B）。

2 基于if-then规则下离散的Znumber的算法

假定两个Z-valuation信息,其中

假设“*”是一种运算,则X*Y=Z=其中Z是X和Y的运算结果,基于此,if-then规则下两个Z-number的算法就可划分为四个部分,A1和A2之间的值的算法,A1和A2之间隶属度的算法,B1和B2之间的值的算法,B1和B2之间隶属度的算法。基于Jiang等[5]的推理过程:

其中

A=A1*A2,B=μA·（pX*p Y）,其中“·”仅仅描述隶属度和潜在概率之间的联系。p X和p Y受 限 制 于

(1)A的值可由…,x2*y s2,…,x s1*y1,…,x s1*y s2}计算,其中有些不同的x j和y k关于*的运算结果是相同的,即z i=x j1*y k1=x j2*y k2=…则隶属度μA可由

计 算,其 中min是 在μA1（x ja） 和μA2（y k a） 之间的取值,a=1,2…,而max是对

(2)考虑B1和B2的计算,其过程与潜在概率p X和p Y有关。X和Y的概率分布表示为｛pX1,…｝和｛pY1,…｝,需 要 注 意 的 是,这 里p X j的表示X的第j组概率分布,Y和Z也是如此。每一个p X j和p Yk都有其相应的隶属度μ（p X j） 和μ（p Yk） ,其 中μ（p X j） 是μB1（b1j）,min处理后的值再进行取值。μ（p Yk） 是μB2（b2k）。考虑到实际情况,p Z的隶属度计算如下:

也可写作公式

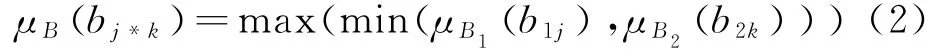
其中1≤j≤t1,1≤k≤t2。受限制于

(3)考虑Z-number限制部分b l的计算

①构建优化模型

输出Z-valuation信息的潜在概率信息的计算可以转化为一个优化模型,此限制基于线性相关方程:

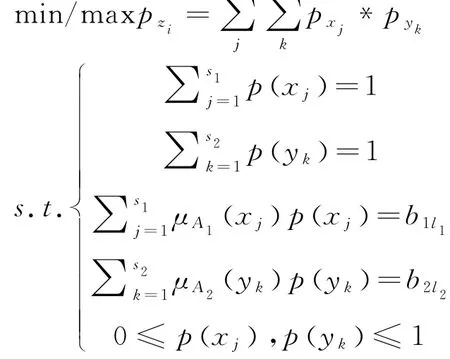
其中1≤l1≤t1,1≤l2≤t2,这里得到的仅仅是t1*t2组区 间概率 信 息［minp（z i）,maxp（z i）］,每一组区间概率信息({[minp(z1),maxp(z1)],…[minp(z s),maxp(z s)]},意味着有无限组概率分布,不利于最后限制部分的计算。基于此,可利用最大熵方法获得最可能的潜在概率分布。

②优化区间信息

随着优化模型和给定数据的变化,①中得到的区间不一定能够满足最大熵方法中的约束条件,需要优化区间信息。具体方法如下:

对于t1*t2组区间信息分别进行如下操作,以一组区间信息

然后将原来的区间可以改写为

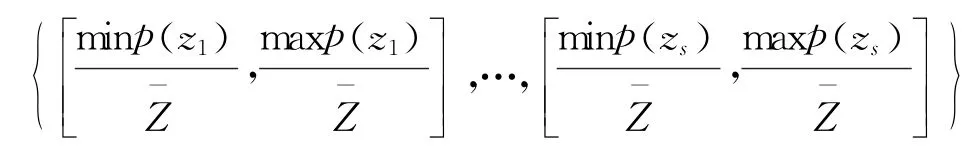
最后令

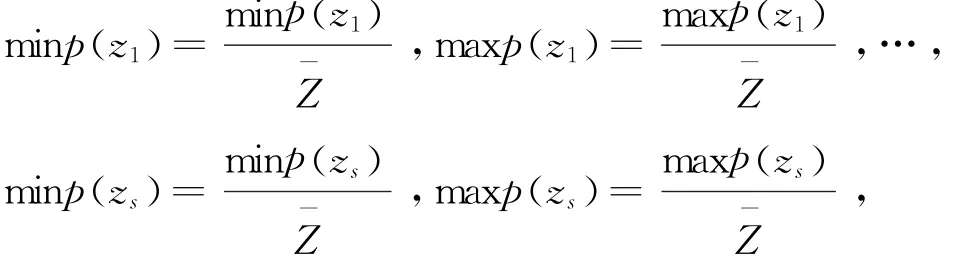
得到新的区间

{[minp(z1),maxp(z1)],…[minp(z s),maxp(z s)]}

③建立最大熵模型

由此得到最可能的概率分布,模型如下:

④计算得到b l

通过③得到t1·t2组最可能的概率分布,通过公式可以得到b1,b2,…,b t,其中t=t1·t2

3 Z网络的结构以及算法

Z网络由两部分组成:结构G和参数θ。网络结构G是一个有向无环图,描述属性之间的依赖关系;参数θ量化网络,其中包括每个属性的条件概率表。Z网络的构建过程如下:找到整个研究系统中涉及的全部随机变量,将其绘制成有向图,如图2是一个简单的Z网络,其中圆代表随机变量,箭头表示依赖关系[9]。图2中有三类小结构,而且由这三类小结构就能构成所有的Z网络。如图1所示,三类小结构分别为结构1、结构2、结构3。接下来介绍一下这3种结构。

图1 (a)结构一(b)结构二(c)结构三

图2 简单Z网络

结构1

如图1(a)所示,X,Y,Z是三个Z-valuation信息,X和Y分别有一个箭头指向Z,代表由X和Y可以推出Z,箭头代表它们的推理关系,表示为p（Z|X,Y）。结构中X和Y是输入值,Z是输 出 值。推 理 过 程:X=（A1,B1）,Y=（A2,B2）,Z=（A,B）=X·Y

其中

首先如果p（z i|x j,y k）≠0,就说x j和y k可以推出z i,那么隶属度μA（z i）就可以由公式（1）计算,解释参考第二部分中隶属度的求法。

第二,从优化模型

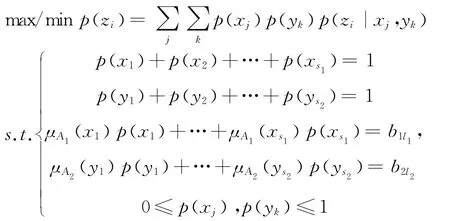
(其中i=1,2,…,s,j=1,2,…,s1,k=1,2,…,s2,l1=1,2,…,t1,l2=1,2,…,t2)得到p（z i）的区间值［minp（z i）,maxp（z i）］。优化区间信息,具体步骤可见2中④,利用最大熵方法maxp（z i）log2p（z i）

得到t1·t2组概率分布p Zl,其中l=1,2,…,t1·t2,每组概率分布p Zl都是｛p（z1）,p（z2）,…,p（z s）｝的形式。而且每组有相应的隶属度μB（p Zl）,由公式（2）计算。最后,得到了μA（z i）和p Zl,b l便可由公式（3）计算得到,其中的p（z1）,p（z2）,…,p（z s）是第l组概率分布中的概率,b l的隶属度就是μ（p Z l）,即μB（b l）=μB（p Zi） 。

结构2

如图1(b),X,Y,Z是三个Z-valuation信息,X和Y,X和Z之间有一个箭头,这代表由X中的信息可以分别推出Y和Z中的信息,其中X是输入信息,Y和Z是输出信息。箭头代表因果关系,分别由p（Y|X）和p（Z|X）表示,推理过程:

其中A1,B1,A2,B2,A,B与结构一中的一样。

首先,如果p（zi|x j）≠0,则说明由x j可以推出z i,如果p（yk|x j）≠0,则说明由x j可以推出y k。其隶属度由公式（1）计算,其中输入信息只有X,故min只对不同的x j的隶属度取值,即max可省略。其次,我们可以利用两个优化模型分别得到p Y和p Z。

(其中i=1,2,…,s,j=1,2,…,s1,k=1,2,…,s2,l1=1,2,…,t1)由此得到区间信息,优化区间信息使用最大熵方法得到t1组概率分布p Zl和p Yl2,而μB（p Zl） 和μB2（p Yl2）由公式（2）计算。最后,计算出了μA（z i）和p Zl,μA2（y k）和p Yl2,那么可由公式（3）计算b l和b l2,其隶属度μB（b l）和μB2（b l2）就等于相应的μB（p Zl）和μB2（p Yl2）。

结构3

如图1(c),X,Y和Z是三个Z-valuation信息。X中的信息可以通过Y传到Z。其中X是输入信息,Z是输出信息。箭头代表因果关系,表示为p（Y|X）和p（Z|Y）。推 理 过 程:X=（A1,B1）,Z=（A,B）,其中A1,B1,A,B与结构1中的一样。

首先,如果p（yk|x j）*p（zi|y k）≠0,代表z i可由x j经y k推出,其隶属度可由公式（1）得到。其次建立优化模型

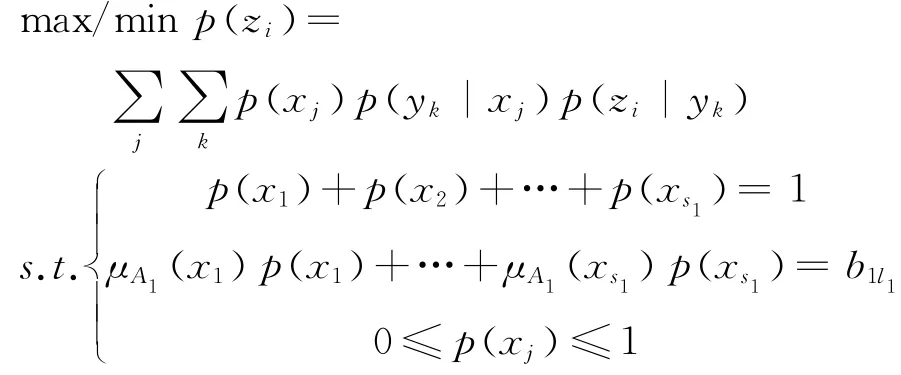
(其中i=1,2,…,s,j=1,2,…,s1,k=1,2,…,s2,l1=1,2,…,t1),由此得到t1组区间信息,优化区间信息使用最大熵方法得到t1组概率分布,相应的隶属度μB（p Zl） 由公式（2）计算。最后算出μA（z i）和p Zl,由公式（3）计算b l,其中p（z1）,p（z2）,…,p（z s）是第l组概率分布中的概率,隶属度μB（b l）就是μB（p Zl）。

4 实例分析

表格1

?

污染指数的确定是一大难题,利用Z网络及其算法可以实现。通过某地区的湿度和风力情况,结合Z网络模型判断其污染指数。现有一个三层Z网络,如图3所示,其中X,Y,Z,M,N都是Znumber,分别代表空气湿度(x1:低,x2:正常,x3:高),风力(y1:小风,y2:中风,y3:大风),天气(z1:晴,z2:多云,z3:雨),风沙量(m1:少量,m2:中等,m3:多),污染指数(n1:轻度,n2:中度,n3:重度)。其条件概率如表所示,输入专家评价的空气湿度（X,A1,B1）和风力情况（Y,A2,B2）,其中

首先由推理算法可知,如果p（n i|m a,z l）·p（ma|y k）·p（z l|x j,y k）≠0,表示由x j和y k可推出n i,或者称污染指数可由空气湿度和风力推断出。由公式

能够计算

其次,根据Z网络的基础结构构建这个三层网络的优化模型:

基于此优化模型利用前面步骤得到四组区间值。优化区间信息利用最大熵模型得出p N:

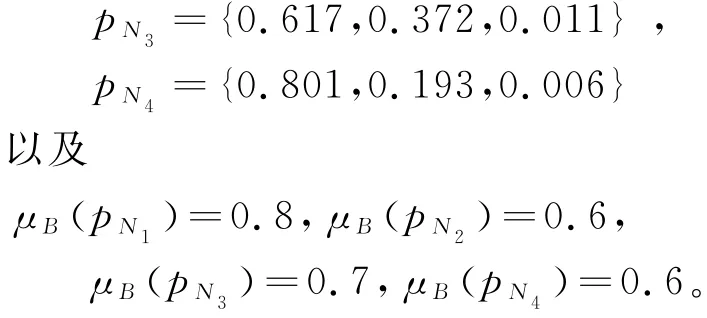
最后由公式（3）得到b l:

代表在专家评价的空气湿度和风力情况的条件下,推理出污染指数是轻度和中度的结果较高,其中B是A的可靠性,0.7974,0.7993,0.7989,0.7994是A的概率,代表着A较为可靠。

5 结 语

在Z-number和Z网络理论的基础上,对原来的推理算法作出了改进,实现了关于Zvaluation的不确定性推理。在通过最大熵方法来实现潜藏概率的获取之前,对由优化模型获取的区间值概率进行了优化,从而使得模糊不确定性推理变得更加完善,然后将改进后的算法运用到决策分析中。在这里考虑的情况并不全面,Z网络的结构还比较简单,改进后的推理算法并没有应用到更加复杂的Z网络中,针对实际中的各种问题,还需要继续研究。