基于IALO算法的蓄电池参数辨识
2021-11-01吴忠强王国勇谢宗奎卢雪琴何怡林
吴忠强,王国勇,谢宗奎,卢雪琴,何怡林
(燕山大学 河北省工业计算机控制工程重点实验室,河北 秦皇岛 066004)
1 引 言
随着能源危机的日益加重,新能源汽车代替燃油汽车成为各国可持续发展的重要举措。相对于传统汽车,电动汽车在能量补给速度方面存在一定的劣势,因此动力电池充放电成为制约电动汽车推广的关键因素。动力电池模型的建立以及模型参数的精确辨识是对电池电量进行高效利用和优化控制的前提[1~3]。
蓄电池模型是研究蓄电池充放电性能的主要载体。常用的蓄电池模型主要有等效电路模型和电化学模型[4]。电化学模型主要研究动力电池内部电化学反应过程,是一种精确的电池模型,由于计算复杂,仅适用于理论研究[5];等效电路模型是目前应用最广泛的电池模型,由电池内阻、极化电容和电压源等理想电路元件组成,采用线性变参数方法(linear parameter varying, LPV)来模拟蓄电池的非线性工作特性[6]。等效电路模型精度略低于电化学模型,但相比电化学模型具有参数少、计算简单、便于实时估计等优点[7]。目前,常用的等效电路模型有Rint模型、RC模型、PNGV模型和Thevenin模型等。Thevenin模型具有更好的动态适应性,可以很好地模拟电池的动态特性且结构简单[8],在蓄电池的建模及荷电状态(SOC)估计中的应用也最广泛[9]。
目前,常用的等效电路模型参数辨识方法有最小二乘法,遗传算法,粒子群优化(particle swarm optimization, PSO)算法等。文献[10,11]采用最小二乘法对电池等效电路模型中各元件参数进行辨识。最小二乘法原理简单、便于实现、收敛速度快,但只适用于线性系统的参数辨识。基于遗传算法的等效电路模型参数辨识[12,13],是将估计出的参数做I-V拟合,利用每次迭代减小误差得到参数,适用于非线性系统的参数辨识,但设定参数较多,编程复杂,优化时间较长。基于粒子群优化算法的蓄电池参数辨识[14,15],该算法结构简单,搜索速度快,易于工程实现[16],但易陷入局部最优,全局搜索能力差。近几年,许多智能优化算法也被应用到蓄电池等效电路模型的参数辨识中。文献[17]采用布谷鸟算法辨识电池模型参数,该算法结构简单、参数少,在处理优化问题时不需要重新匹配参数,缺点是辨识电池模型参数时容易陷入局部最优,迭代后期种群更新缓慢。文献[18]采用细菌觅食算法对蓄电池模型进行参数辨识,该算法并行搜索,不易陷入局部最优,鲁棒性强,找到全局最优解的概率高,但是算法的收敛速度较慢。
针对上述算法在蓄电池参数辨识中的问题,本文提出了一种基于改进蚁狮优化算法(improved ant lion optimization, IALO)的蓄电池参数辨识方法。针对蚁狮优化算法(ant lion optimization, ALO)存在收敛速度较慢与精度较低的问题,引入混沌Logistic映射初始化,使初始化群体遍及解空间,有利于寻找全局最优解;引入自适应惯性权重加随机柯西变异策略,提高算法收敛速度;引入精英反向学习策略提高群体的多样性,避免算法陷入局部最优解。将3种改进策略相结合,加快了ALO算法的收敛速度,提高算法的寻优精度。
2 蚁狮优化算法
ALO算法是2015年由Seyedali等[19]提出的一种新型智能优化算法,受到蚁狮捕食蚂蚁过程中不断寻找优化问题的最优解启发而提出的。
蚂蚁随机游走表达式为:
xt=[0,cumsum(2r(t1)-1),cumsum, (2r(t2)-1),…,cumsum(2r(tN)-1)
(1)
式中:xt为第t次迭代过程中蚂蚁随机游走后的位置;cumsum为累加和;N为蚂蚁的数目;t为当前迭代次数;r(t)为一个随机函数值,其数学表达式为:

(2)
式中:rand为[0,1]之间的随机数。
蚂蚁随机游走受到蚁狮陷阱收缩影响,其数学表达式为:
(3)
(4)

当蚂蚁在陷阱周围随机移动时,蚁狮会继续挖洞,使蚂蚁慢慢移向自己,数学表达式为:
(5)
(6)
式中:T为最大的迭代次数;w为能够调整蚂蚁移向蚁狮的速度:

(7)
为保证蚂蚁在搜索空间内随机游走,使用式(8)处理:
(8)

蚂蚁当前的位置为:
(9)
式中:At为第t次迭代通过轮盘赌方式选择的在蚁狮周围随机游走的蚂蚁;Et为第t次迭代在精英蚁狮周围随机游走的蚂蚁。
蚁狮捕到蚂蚁后,位置更新公式为:
(10)

ALO算法中轮盘赌的选择机制、蚂蚁的随机游走确保了对搜索空间的开发能力,蚁狮陷阱的自适应性提高了算法的收敛效率[20]。
算法实现步骤为:
步骤1:设置参数,最大迭代次数T、蚂蚁和蚁狮的数目分别为N和M、适应度函数维数D,以及位置变量的上限bu和下限bl。
步骤2:随机初始化蚂蚁和蚁狮的位置,并分别保存在位置矩阵pAnt和pAntlion中,适应度值保存在FAnt和FAntlion中,将适应度进行排序,选出其中适应度值最大的蚁狮作为精英蚁狮个体EAntlion。
(11)
(12)
(13)
(14)
An,d=bl,d+rand(0,1)(bu,d-bl,d)
(15)
Lm,d=bl,d+rand(0,1)(bu,d-bl,d)
(16)
式中:n=1,2,…,N;d=1,2,…,D;An,d表示第n只蚂蚁第d维搜索空间的位置;m=1,2,…,M;Lm,d表示第m只蚁狮第d维搜索空间的位置;bu,d、bl,d为第d维搜索空间的上下限;f[An,1…An,D]表示第n只蚂蚁适应度值;f[Ln,1…Ln,D]表示第n只蚁狮适应度值。

步骤4:游走后的蚂蚁根据式(10)与当前位置最好的蚁狮对比,重新调整最佳蚁狮的位置。如果蚁狮的位置超出了最远边界bu或者bl,则按照最远边界处理,t=t+1。
步骤5:判断是否达到算法的最大迭代次数或精度。若达到,则获得最佳蚁狮位置;否则转至步骤3。
3 改进ALO算法
针对ALO算法在函数寻优过程中存在的估计精度不高、收敛速度慢、易陷入局部最优等问题,提出3点改进:(1) 混沌Logistic映射初始化;(2) 自适应惯性权重加随机柯西变异;(3) 精英反向学习。
3.1 混沌Logistic映射初始化
文献[21]将混沌Logistic映射应用到蜂群算法初始化中,提高了蜂群算法的寻优精度。在优化算法中,初始化种群的方式决定了初始种群的多样性,从而决定了寻优的速度以及解的质量。多数情况下随机初始化产生的初始种群多样性较差,在一定程度上影响了求解的效率。本文采用混沌Logistic映射初始化种群,有望提高种群的多样性和遍历性。
利用混沌算法产生初始解的过程为:
1) 通过式(16)随机产生M个蚁狮初始解,通过式(17)将其映射到Logistic方程的定义域内:
(17)
2) 用Logistic方程进行迭代产生混沌序列:
(18)
式中:μ为3.57到4之间的随机数,当μ取4时,完全进入混沌状态。
3) 将产生的混沌序列映射回原来的定义域内:
(19)
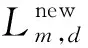

3.2 自适应惯性权重加随机柯西变异
文献[22]提出了一种非线性惯性权重下降策略并应用到鲸鱼优化算法(whale optimization algorithm, WOA)中,惯性权重对智能优化算法的收敛速度和全局寻优能力都有重要影响。实验证明,较大的惯性权重有利于粒子全局寻优,反之,则利于局部开发。文献[23]引入柯西变异策略并应用到PSO算法中,有利于增加种群多样性以减小陷入局部最优的概率。为了提高ALO算法的寻优能力,本文提出一种以当前最优蚁狮位置为中心的自适应惯性权重加随机柯西变异策略,协调全局搜索和局部开发能力,进而提高算法收敛速度与寻优能力,表达式为:
(20)
Lm,d=WLm,d+z1z2Cauchy(0,1) ×(EAntlion,d-Lm,d)
(21)
式中:W(t)为第t次迭代的权重值;g、h为自适应权重常数项因子;z1、z2为0到1之内的随机数;Cauchy(0,1)是服从标准柯西分布的随机数;EAntlion,d为蚁狮最优个体。
3.3 精英反向学习策略
策略2中采用的随机柯西变异策略变异范围的中心为最优个体位置,这一定程度上限定了个体变异的多样性,因此,为了进一步增加算法寻优过程中种群多样性,群体更新过程中引入精英反向学习策略。Shahryar等[24]已证明反向候选解可以更大概率接近全局最优解,反向学习策略现已被成功应用到粒子群算法[25]、差分进化算法[26]等算法的优化中,用于拓展种群的搜索区间,提高算法的性能。
精英反向学习策略过程为:
1) 根据现有种群生成其反向解种群:
(22)
2) 当反向解超过边界时,对反向解进行重置:
(23)

(24)
(25)
式中:Ji,d代表第i个精英个体第d维搜索空间的位置,i=1,2,…,P;Pj,d代表第j个普通个体第d维搜索空间的位置,j=1,2,…,(N-P)。
4) 精英群体反向解和普通群体构成新种群。
4 算法测试与分析
为了验证所提算法的优越性,选取5个标准测试函数将IALO与ALO、自适应粒子群优化算法(adaptive particle swarm optimization, APSO)和樽海鞘优化算法(salp optimization algorithm, SSA)的性能进行比较。设置算法参数:IALO算法中,自适应权重常数项因子为:g=3、h=2。APSO算法中,学习因子c1=1.494 45、c2=1.494 45;惯性权值上下限ωmax=0.9,ωmin=0.4;速度更新上下限vmax=1,vmin=-1。SSA算法中,移动方向概率阈值r3=0.5。4种算法种群规模、迭代次数、粒子空间维数统一设定为:n=40、T=500、D=10。4种算法分别独立运行10次,并对运行所得的最优值、均值与方差进行比较,结果见表1。
从表1可看出,APSO最优值达到10-4,ALO最优值达到10-9,SSA的最优值达到10-10,IALO最优值达到零,IALO的寻优精度优于前3种算法。从测试函数的均值和方差可以看出,APSO对于测试函数的均值和方差大都在10-2和10-4左右,SSA对于测试函数的均值和方差大都在10-5和10-11左右,ALO算法对于测试函数的均值和方差大都在10-5与10-12左右,而IALO的对于测试函数的均值和方差大都在10-36和10-80左右,因此,相比较前3种算法,IALO具有更强的寻优能力和稳定性。

表1 PSO、SSA、ALO和IALO的估计精度Tab.1 Estimation accuracy of APSO,SSA,IALO and ALO
本文对4种算法的收敛速度也进行了比较,将运行10次的适应度值取平均值,结果显示:SSA对于多数测试函数迭代250~300次达到收敛,APSO对于多数测试函数迭代200~250次达到收敛,ALO对于多数测试函数迭代150~200次达到收敛,IALO对于多数测试函数迭代5~20次就达到收敛,因此,相比前3种算法,IALO收敛速度更快。
5 蓄电池建模与参数辨识
选用的电池模型为三阶戴维南等效电路模型[27],如图1。

图1 三阶电池模型Fig.1 Third-order model of a battery
电路中包含1个理想电压源、1个电阻,3个RC环。将3个RC环两端的电压作为状态变量,电流作为输入变量,模型端电压作为输出变量,列写电池模型的离散状态空间表达式:
(26)

(27)

利用IALO算法对电池模型电阻、电容参数进行辨识,将放电电流iL作为系统输入,电池端电压uL作为输出,待辨识参数包括uoc、Δuoc、R0、R1、R2、R3、C1、C2以及C3等9个参数。算法的目标函数为:
(28)
蓄电池是容量为12 V/50 A·h的铅酸蓄电池,利用PITE 3980智能放电监测仪采集电池组放电电压、电流实验数据。实验平台见图2。

图2 蓄电池实验测试台Fig.2 Test bench of battery
先采用4 A电流对蓄电池进行放电1 h,静置0.5 h;再采用3 A放电电流对蓄电池放电1 h,静置0.5 h;最后采用2 A放电电流对蓄电池放电1 h。每隔4 min取1次实验数据,得到的电池端电压曲线见图3,由图可以看出:放电电流越大,电压下降越快。
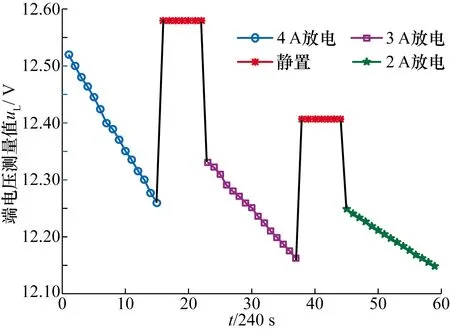
图3 端电压曲线Fig.3 Curve of terminal voltage
基于蓄电池的放电实验数据,采用ALO与IALO算法辨识模型参数。统一设置算法参数:种群规模n为30,最大迭代T为1 000,粒子空间维数D为9,辨识模型10次。分别取两算法最优适应度值的9个参数辨识结果如表2,端电压的最优估计曲线见图4。

表2 模型参数辨识结果Tab.2 Identification result of model parameters
由图4可看出,IALO和ALO算法的辨识结果与测量值基本重合,均有较好的辨识精度。为了更清楚地观察辨识结果,给出辨识结果的误差曲线见图5。图中,ALO算法估计误差值在-0.02~0.015之间;IALO算法估计误差值在-0.005~0.006之间,辨识误差较小。
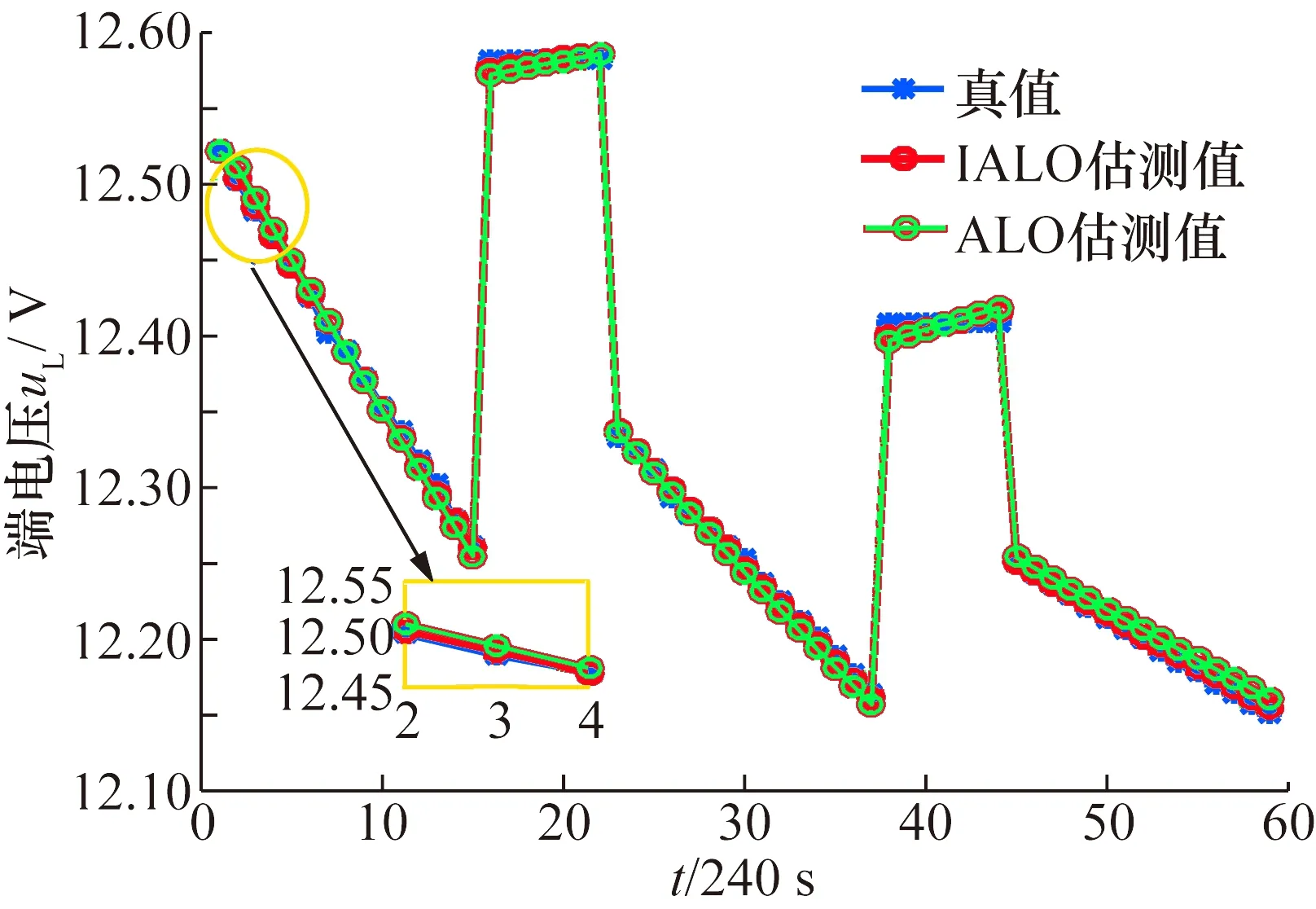
图4 端电压拟合比较曲线Fig.4 Fitting curve of terminal voltage

图5 端电压估计误差曲线Fig.5 Terminal voltage estimation average error curve
为了进一步说明IALO算法的准确性,取10次辨识结果的均方误差MSE、平均绝对百分比误差MAPE和平均绝对误差MAE作为拟合准确率的评价指标。均方误差MSE是反映估计量与被估计量之间差异程度的一种度量;平均绝对百分比误差MAPE反映预测效果;平均绝对误差MAE是绝对误差的平均值,能更好的反映预测值误差的实际情况,3种评价指标取值越小越好。两算法3种误差的平均值见表3。MSE、MAPE及MAE的定义分别为:
(29)
(30)

(31)
由表3可看出,IALO算法相比ALO算法的MSE、MAPE、MAE分别小2.252×10-4,4.207×10-4,2.866×10-3,辨识精度更高。
6 结 论
等效电路模型的选择和模型参数的辨识精度,对蓄电池荷电状态的准确估计具有重要意义。提出了一种改进蚁狮优化算法,引入混沌Logistic映射初始化,有利于寻找全局最优解;引入自适应惯性权重加随机柯西变异策略,有利于提高算法收敛速度;引入精英反向学习策略可以有效地提高群体的多样性,避免算法陷入局部最优解。5个标准测试函数的寻优结果表明:IALO相比于PSO,SSA,ALO算法寻优精度更高,收敛速度更快,将IALO应用于三阶Thevenin等效电路模型参数辨识中,得到更小的估计误差,验证了IALO算法的有效性。
