基于GWO的SVM在红外甲烷传感器测量误差分析中的应用
2021-11-01陈红岩刘嘉豪盛伟铭赵永佳
陈红岩,刘嘉豪,盛伟铭,黄 瀚,赵永佳
(1. 中国计量大学 现代科技学院,浙江 杭州 310018; 2.中国计量大学 机电工程学院,浙江 杭州 310018)
1 引 言
天然气的主要成分为甲烷,在使用中需要对甲烷气体进行检测。现在红外甲烷传感器具有精度高、使用寿命长等优点,被广泛用于气体的测量,所以如何进一步减小甲烷气体的测量误差成为一个被关注的问题[1,2]。
近年来,径向基(RBF)、小波神经网络以及SVM等在数据处理领域有了广泛应用。不断涌现出的算法也为气体定量分析和数据仿真提供了新的途径,如Ali Gulbag等提出一种应用在混合气体浓度定量识别中的径向基函数神经网络降维方法,简化了数据集,加快了收敛速度[3];杨景明等采用改进果蝇算法与最小二乘支持向量机相结合的方法,用于铝热连轧现场数据的仿真,减小了预测误差[4];吴永忠等以RBF网络为核心提出了一种新型甲烷定量分析模型,有效减少了环境温度和难以满足朗伯-比尔定律约束条件带来的误差[5];梁杰等以前向和反向两种修正算法为基础,提出了一种多级修正模型,解决了车载气体传感器测量结果不易修正及准确度低的问题[6]。
本文用实验室研制的红外甲烷传感器对浓度在0~5.05%范围的25组标准甲烷气体进行测量,选取其中20组样本作为训练集,使用不同算法和SVM结合建立了多种回归模型,其余5组样本作为测试集用来验证模型的预测精度。通过计算对比表明,基于灰狼优化算法(grey wolf optimization,GWO)的支持向量机(support vector machine,SVM)更具优势。
2 SVM回归模型
支持向量机SVM是一种统计学习理论回归方法[7,8]。其主要思想是将输入数据(低维空间)映射到高维特征空间,然后构造一个核函数来实现线性回归函数。
本文将已知浓度的甲烷气体样本和相对应的红外甲烷传感器测量输出的电压差值比作为数据集T={(x1,y1),…,(xN,yN)}∈(R×R),其中xi∈R为红外甲烷传感器输出的电压比值,yi∈R为对应的甲烷气体浓度值,i=1,2,…,N。按照式(1)进行回归分析。
f(xi)=ω·φ(xi)+b
(1)
式中:ω·φ(xi)为向量ω与φ(xi)的内积;ω为回归系数;φ(xi)为输入空间到特征空间的映射函数;b为阈值。
在此引入松弛变量ξ,ξ*≥0求解ω与b,根据SRM准则,将式(1)转换为凸二次规划问题:
(2)
(3)
式中:正则化参数C为惩罚因子;ε为不敏感损失函数。
引入Lagrange函数求解式(2),通过核函数k(xi,xj)将高维空间的内积运算转换在原二维空间计算,有:
(4)
得到的SVM回归模型的回归函数为:
f(x)=ω·φ(x)+b
(5)
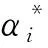
在非线性情况下,一般的核函数是高斯径向基核函数(RBF),其表达式如式(6):
K(xi,xj)=exp(-g||xi-xj||2),g>0
(6)
式中:g为gamma参数函数设置(若k为属性的数目,则g默认为1/k)。
在支持向量机模型中,惩罚因子C和核函数自带参数g的取值将对训练数据和预测数据的精度产生较大影响。惩罚因子C即对误差的宽容度,C过大或过小都会产生不好的影响(过拟合和欠拟合)。参数g隐含地决定了数据映射到新的特征空间后的分布,g的大小和支持向量的个数息息相关。因此,寻找最优参数至关重要。
3 GWO-SVM模型
3.1 GWO算法
2014年,澳大利亚学者Mirjalili等提出了一种新的元启发式算法——GWO[9]。该算法的灵感来自于灰狼,是一种模仿了灰狼的等级关系和自发的捕猎行为来实现目标优化的新型群智能优化方法,具有较强的收敛性、参数小、易实现等特点。在该方法中,把狼群分为4个社会阶级α、β、δ、ω(其中α最高,ω最低),如图1所示。
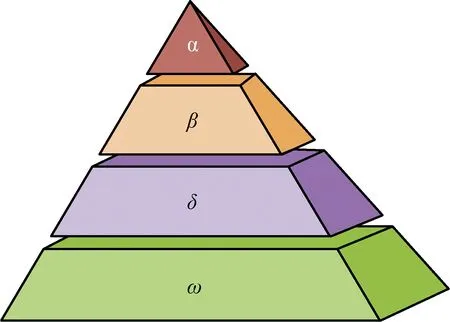
图1 灰狼等级制度(从上到下递减)Fig.1 Grey wolf hierarchy
上层阶级领导指挥开展狩猎行动,GWO算法的具体步骤如下:
1) 包围猎物:进行狩猎行动时,狼群会先开始包围猎物。这种包围行为的数学建模为:
(7)
2) 追捕猎物:灰狼可以搜索猎物的位置和猎杀它们,这种行为通常由α阶层指导,目前为止获得的前3个最佳位置会被保存,并要求其他搜索代理(包括ω)根据最佳搜索代理的位置更新其位置。这种行为的数学建模为:
(8)
3.2 GWO-SVM
在支持向量机参数优化方法中,GWO方法在复杂搜索空间的全局搜索中具有传统方法所不具备的优势。此外,与人工神经网络等其他机器学习算法相比,GWO-SVM模型更适合小样本数据而不是大样本数据,而且具有更好的学习效果[10]。
样本大小以30个单位为界,因此本次实验的样本数据属于小样本数据,完全契合GWO-SVM模型的使用范围。基于GWO的SVM参数优化过程如图2所示。
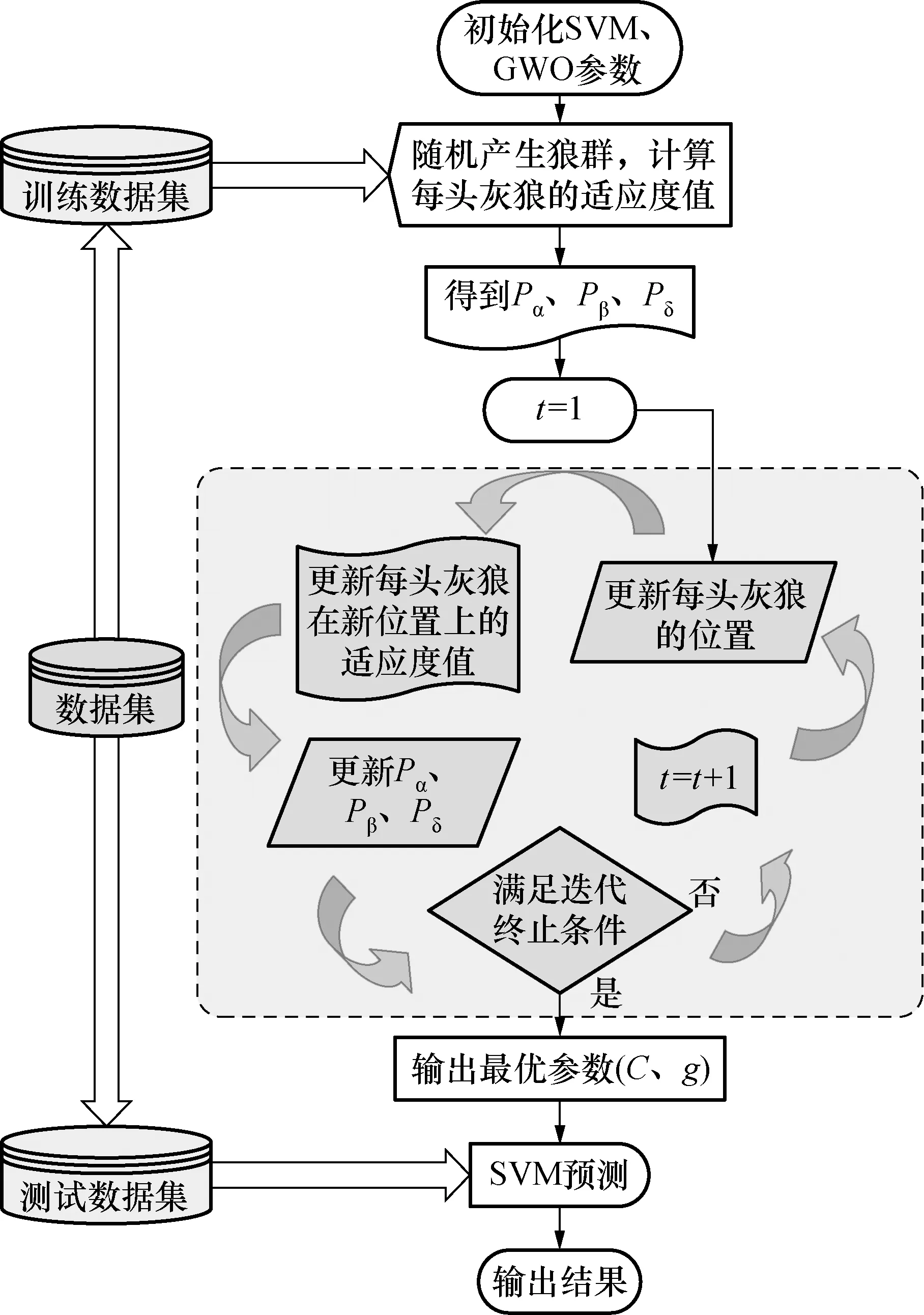
图2 GWO-SVM模型流程图Fig.2 Model flow chart of GWO-SVM
4 实验及数据分析
实验采用基于Non-Dispersive InfraRed(NDIR)原理制作的甲烷传感器对甲烷气体进行检测[11,12]。向甲烷传感器气室中充入待测浓度的甲烷气体,当MCU调制的红外光源通过气室时,由于甲烷对特定波长的红外光有吸收,因此当特定波长的红外光通过待测气体后,在特征吸收峰附近的红外能量会被全部吸收,导致光强的衰减,探测器将检测剩余的光强度并转化为电信号,经过信号调理电路处理后作为模型的输入,其原理如图3所示(U1、U2分别为测量通道和参考通道的电压值)。图4、图5为红外甲烷气体传感器和实验采样图。
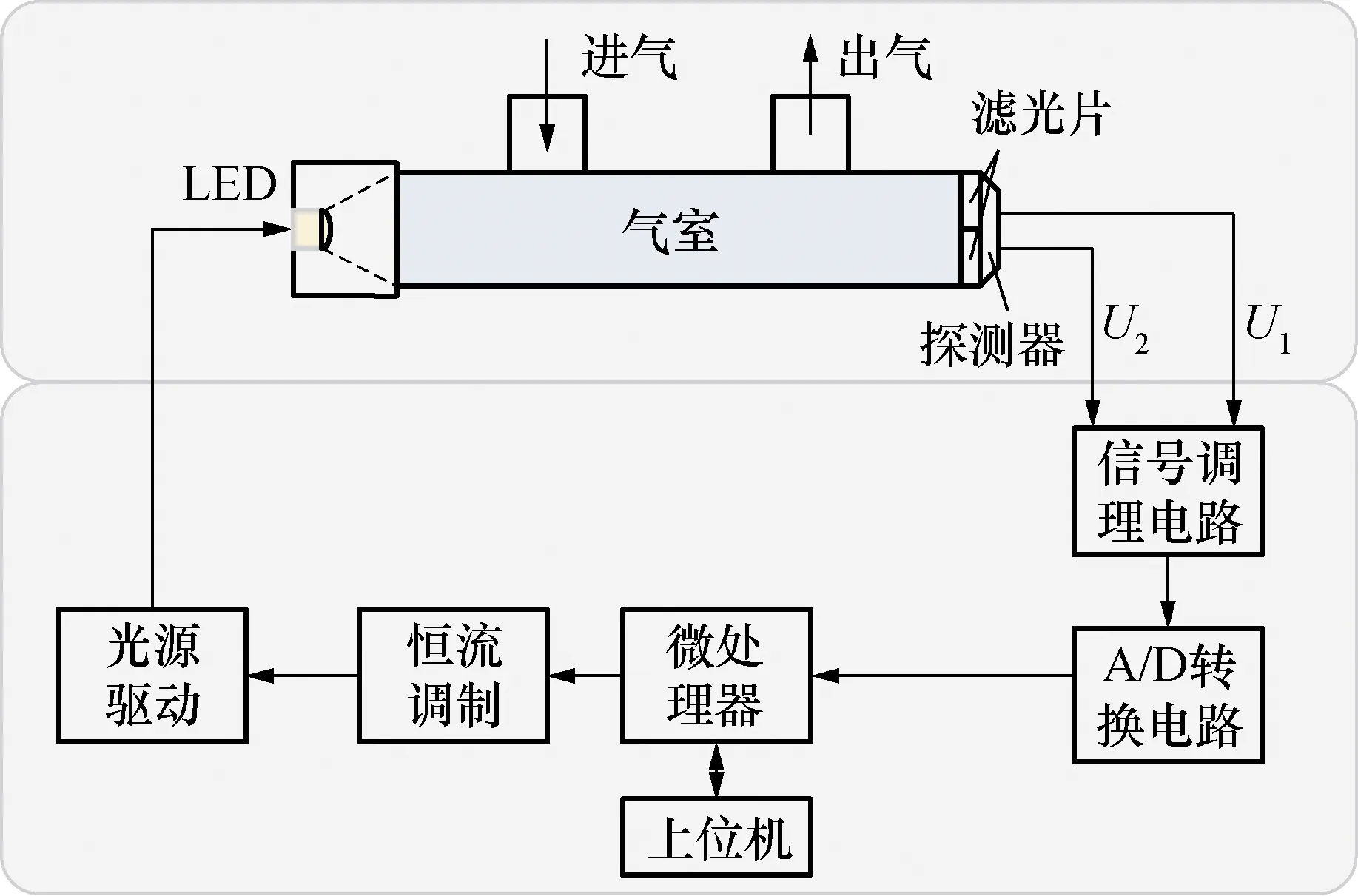
图3 甲烷气体测量系统原理图Fig.3 Methane gas detection schematic diagram

图4 红外甲烷传感器结构Fig.4 Infrared methane sensor

图5 实验采样系统Fig.5 The experimental sample
本次实验用红外甲烷传感器对0~5.05%浓度范围的25组标准甲烷气体进行测量[13]。根据朗伯比尔定律(Lambert-Beer law)对气体浓度公式进行推导后发现,对于一个确定的传感器系统而言,只需得到测量通道和参考通道的电压差与参考通道电压的比值即可求出气体浓度,因此把这个电压差值比作为最终输出。从中选取20组数据作为训练集,用3种不同的方法各自建立SVM回归模型,对比3种模型的回归效果。把剩余浓度分别为0.18%、0.94%、2.01%、3.13%、4.53%的5组数据作为测试集,用已建立好的回归模型进行预测,验证SVM回归模型的预测精确度,检测数据如表1。

表1 甲烷传感器采样数据Tab.1 Methane sensor sampling data
SVM回归模型的建立需要找到最优的惩罚因子参数C和RBF核函数参数g,本文采用的基于GWO的SVM方法进行参数寻优的步骤如下[14,15]:
1) 输入训练集和测试集。
铁路系统中的各设计单位正在大力推广基于BIM的设计技术,咨询单位对BIM的研究、应用成熟度,需与设计单位基本同步。
2) 初始化GWO、SVM参数,随机产生狼群,每个狼群位置即为C、g。
3) 计算每头灰狼的适应度值,根据适应度值将狼群分为4个阶级α、β、δ、ω,进行迭代。
4) 更新每头灰狼的位置和每头灰狼在新位置上的适应度值。
5) 判断是否满足迭代终止条件,若满足,则停止迭代,输出SVM中C和g的最优值;不满足,则转到步骤4),当所得参数组合不唯一时,取C最小的组合。
为了显示通过GWO算法进行SVM参数寻优的优势,与目前普遍使用的GridSearch法和PSO算法进行SVM参数寻优建立的回归模型进行对比。训练集在3种算法建立的SVM回归模型上的验证效果如图6~图8所示。
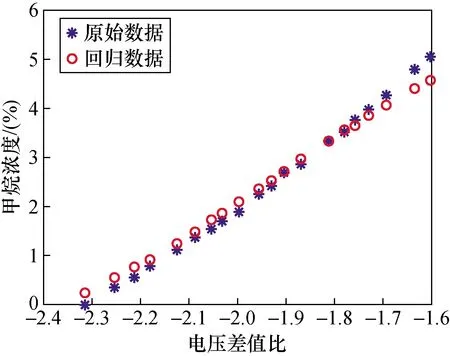
图6 基于网格搜索法的SVMFig.6 SVM based on Grid Serach

图7 基于粒子群优化算法的SVMFig.7 SVM based on PSO

图8 基于灰狼优化算法的SVMFig.8 SVM based on GWO
由图6~图8可知,图8所采用的基于灰狼优化算法的SVM建立的回归模型效果最好。表2为以上3种方法建立SVM回归模型时的最优参数、寻优时间及其均方差。
由表2可知,采用传统SVM寻优得到的参数C与采用GWO算法寻优得到的参数C范围相差不大,而后者均方根误差明显更小。

表2 模型参数Tab.2 Model parameter
将GWO算法寻优得到的参数代入SVM来建立所需的预测回归模型,并进行预测,得到的预测结果如图9所示。

图9 回归模型预测输出与实际输出对比图Fig.9 A comparison diagram between the predicted output of the regression model and the actual output
图9表明,基于GWO算法寻优建立的SVM回归模型预测曲线和期望曲线很接近,具有很高的预测精度。
3种方法的误差结果对比见表3。

表3 模型预测误差对比Tab.3 Model prediction error comparison (%)
同样,表3表明,基于GWO算法寻优建立的SVM回归模型其绝对和相对误差都明显低于其他2种传统SVM建立的回归模型的误差。
5 结 论
本文将GWO算法应用于SVM的参数寻优,以此建立红外甲烷传感器测量数据的处理模型,并与传统的PSO算法和Grid Serach法所建立的模型进行对比分析。研究结果表明,其回归效果最好,仿真的相对误差小于2%,不仅能满足红外甲烷传感器测量误差的要求,而且对类似测量数据处理的问题,也提供了参考。
