改进TOPSIS法在河南省各市社会发展水平综合评价中的应用

芦果果，赵文英，凤宝林

(牡丹江师范学院 数学科学学院，黑龙江 牡丹江 157011)

过去，人们对社会发展的考察往往从GDP出发，而事实上，GDP反映的仅仅是经济发展的总体状况，对于社会发展的其他方面，如人民生活、科技教育、医疗卫生、社会保障等情况并不能有所结论，故此也就无法对社会发展进行全面、客观地综合评价。特别是对于不同地区，由于地理特征、人口特征、特色产业等方面都具有差异性，如果只把GDP的增长作为评价社会发展的标准，将会造成社会各方面发展的严重失衡。人是社会主体，社会发展应把人的生存、生活所需的条件作为发展重点，经济增长须服从于民生，要选择适合当地地理环境和实际情况的发展方式。因此，想要全方位了解、提升地区的社会发展水平，考虑地区特征显得尤为重要。

近几年，有关社会发展水平的研究不在少数，如：董船、熊丽萍等通过因子分析，对贵阳市 2004-2015 年的经济社会发展情况做了纵向分析比较，对贵阳市今后的发展方向及重点提出适合且可行的建议和意见[1]；高卷等在研究河南省县域经济社会发展水平现状时，利用因子分析法，计算出河南省 109 个县域社会、经济的发展水平的综合得分，并对其进行排名[2]；代金辉等通过聚类分析法和因子分析法，对2015年我国各省社会发展水平进行综合评价与比较，并分析了各地发展的优劣条件及主要特征，客观反映了各个省域的社会发展水平[3]；《云南社会发展水平综合评价研究》课题组依据相关理论及基础数据，结合云南省社会发展的实际情况，第一次对云南的社会发展进行量化与分析，并预测将来云南省的发展方向及特征，对其发展具有现实指导意义[4]；雷沁利用主成分分析，对2016年陕西省各市的社会发展水平进行了综合评价，发现关中地区的社会发展水平要优于陕南和陕北地区，陕南地区的发展最为落后，对此结合实际给出了建议[5]。

已有的关于社会发展领域的研究成果值得肯定，但以往学者对社会发展领域进行研究所选用的数据基本都是 2019年之前的，可能已失去时效性，已有研究成果在指标的选取上考虑得不够全面，所采取的方法可能有一定的弊端，导致结果可信度不高。以河南省各市为研究对象，运用主成分分析改进的TOPSIS法，对2019年河南省各市的社会发展水平进行综合评价，以期为河南省的社会发展贡献一份力量。

1 改进的TOPSIS法

TOPSIS法是20世纪80年代提出的多属性决策模型，历经数十年的实践应用，已在经济、医疗、工程等领域中取得较好的分析效果，但在实际生活中，各个指标对综合评价时所起作用的重要程度往往各不相同，所以对各个指标赋予适当的权重就尤为重要。一共选取了14个指标，这些指标的重要程度很难准确地衡量。利用主成分分析法，对这些指标进行降维，在损失很少信息的前提下，把多个指标转化为几个综合指标，即主成分指标[6]。这几个主成分之间互不相关，且每一个主成分得分本身是有固定权重的，这样既解决了TOPSIS法难以赋予各个指标合理权重的弊端，又避免了指标信息重叠的问题，可以做出更加真实的评价。

改进之后的TOPSIS法的计算步骤如下：

第一，构建社会发展水平指标体系，查找数据，形成原始指标矩阵Xmn，m为样本个数，n为指标个数。

第二，对矩阵X中的指标数据进行标准化，从而消除变量在数量级和量纲上的影响，标准化矩阵为xmn，其公式为：

(1)

(2)

第三，对xmn进行主成分分析，得到k个主成分，设对应的主成分得分为Fk。

第四，将Fk作为新的指标，形成矩阵Zmk，m为样本个数，k为主成分个数。

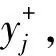
(3)

第六，计算每一个样本与正、负理想解的加权距离D+、D-，方法如下：

(4)

(5)

其中wj为每个指标的权重，这里为每个主成分的方差贡献率的百分比。

第七，计算各评价对象与正理想解的接近程度Ci:

(6)

2 改进的TOPSIS法的应用

2.1 指标体系的构建与数据处理

以河南省18个地市的社会发展水平为研究对象，利用主成分分析改进的TOPSIS法对其进行综合评价与分析，希望为河南省的社会快速发展提供合理建议。

构建社会发展水平的综合评价指标体系。社会发展是一个比较复杂的概念，其内涵和外延都很大，因此涉及的评价指标也较多，在选取指标时，既要全面考虑社会发展的各个方面因素，又要使所选取的数据都具备可获取性。在遵循科学性、代表性的原则下，参考国内外相关文献后[3，7-9]，构建了经济、人民生活、科技与教育、医疗卫生与社会保障、农业与农业现代化五个维度的指标体系，其中包含了14个具体指标，如表1。

根据表1，在河南统计年鉴中查找相关数据，形成原始矩阵X18×14。利用公式(1)、(2)对原始数据进行标准化处理，得到相应的标准化矩阵X18×14，结果如表2：

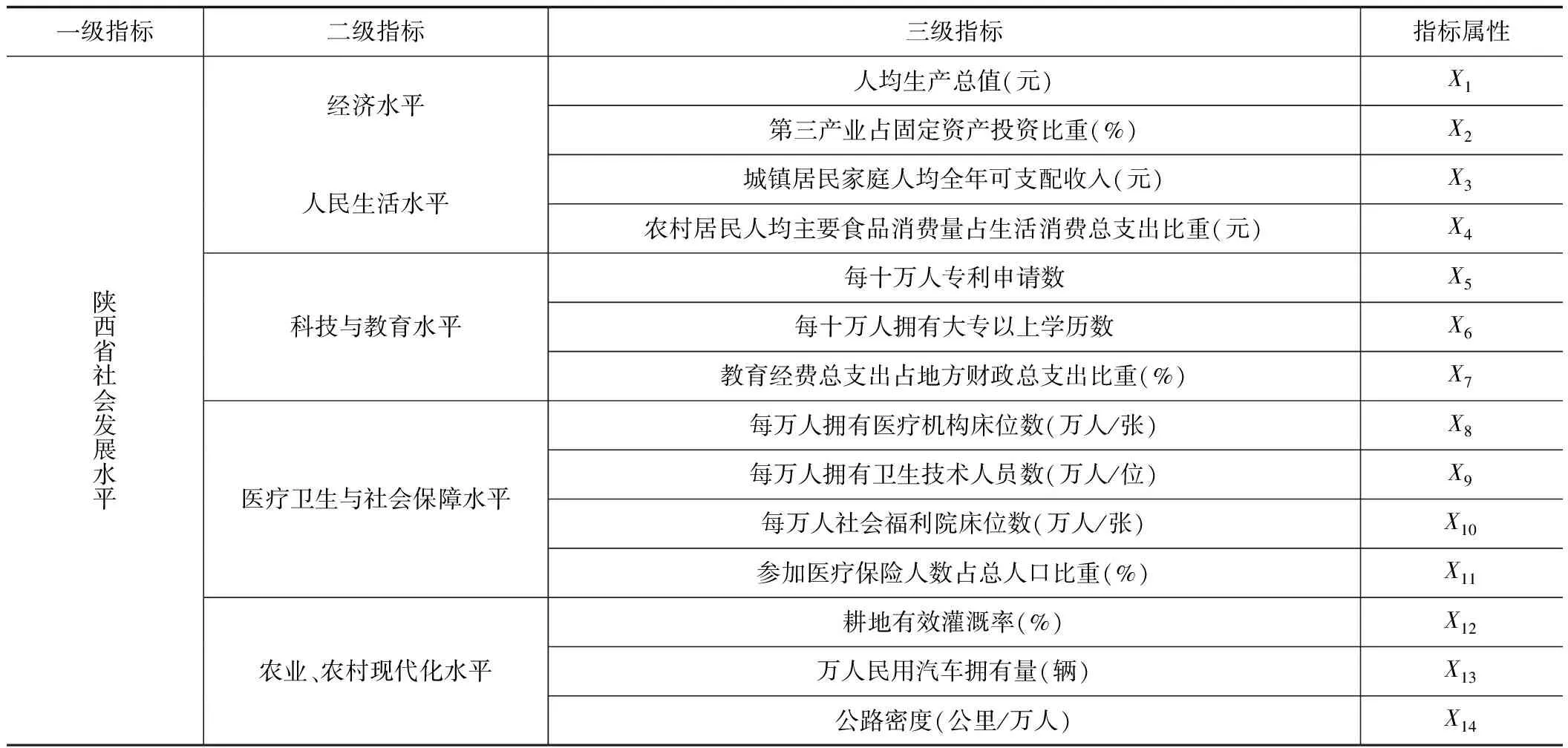
表1 指标体系Tab.1 Indicator system

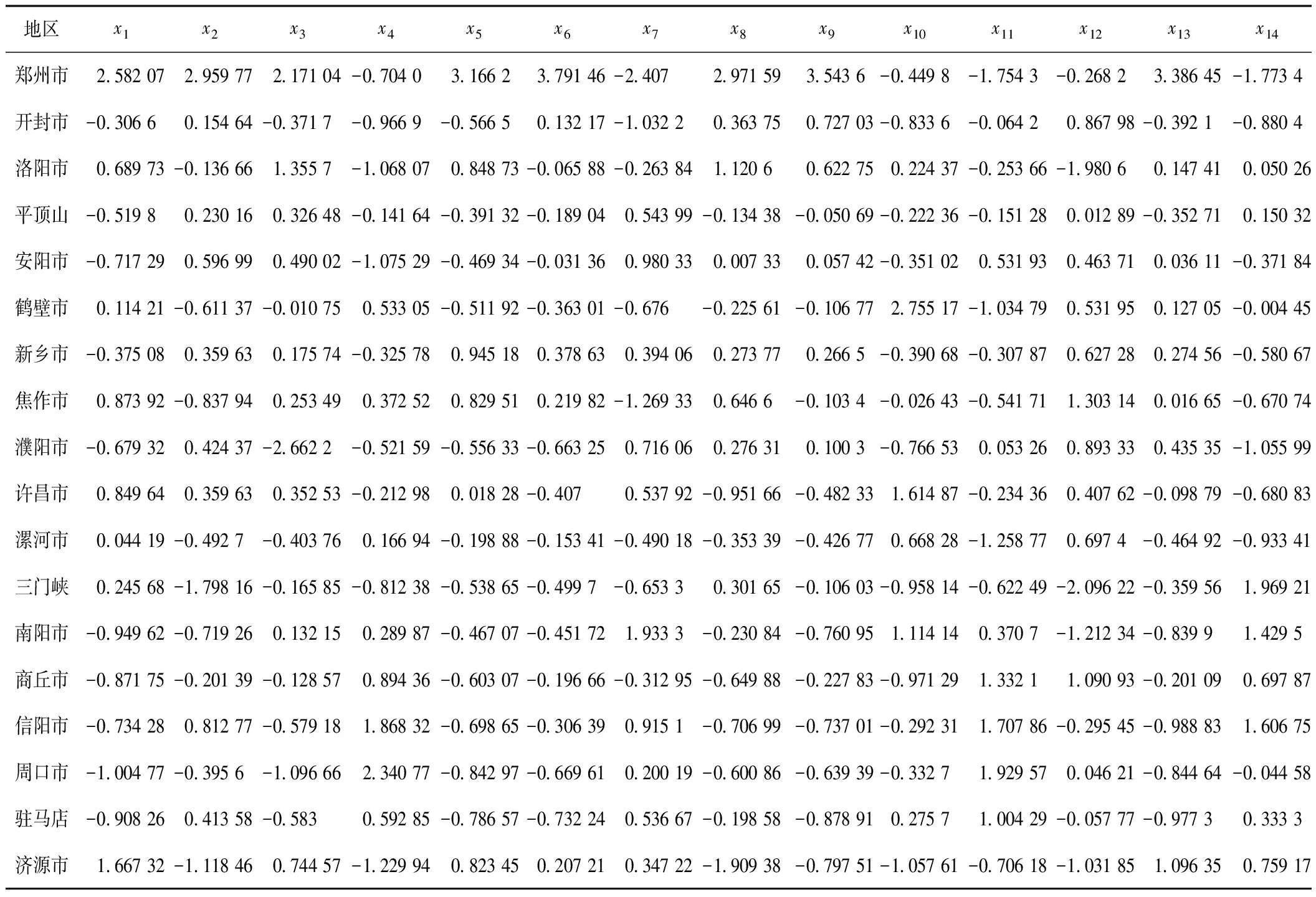
表2 标准化数据Tab.2 Standardized data

2.2 主成分指标的提取

对标准化后的数据进行主成分分析，要对主成分分析做适应性检测，其KMO值为0.614，大于0.6，Bartlett的球形度检验小于0.05，说明指标适合做主成分分析。成分的特征值和方差贡献率结果如表3：

表3说明可以提取出5个主成分，其提取原信息量为原始数据信息量的88.828%。根据成分矩阵分别计算相应的主成分得分，分别记作F1、F2、F3、F4、F5，其相应的权重为：51.631%、14.558%、9.634%、7.525%、5.481%。此时便将原来的14个原始指标简化为现在的5个主成分指标指标，形成矩阵z18×5。

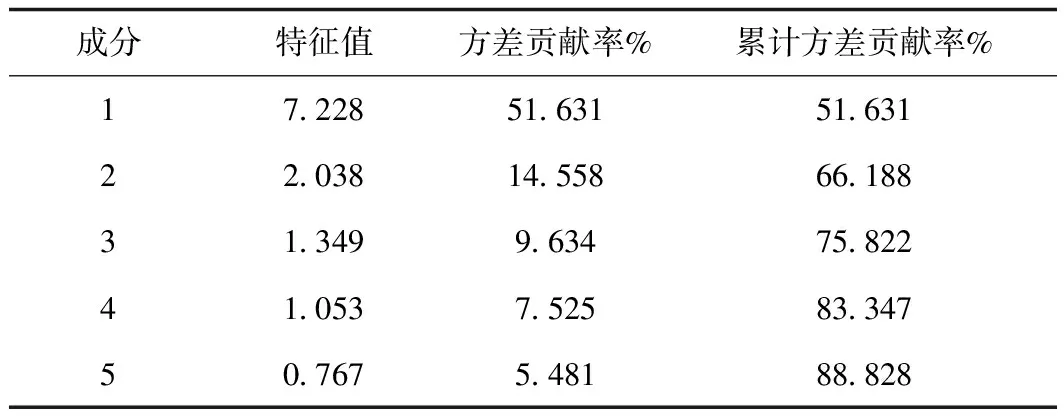
表3 特征值和方差贡献率Tab.3 Eigenvalue and variance contribution rate

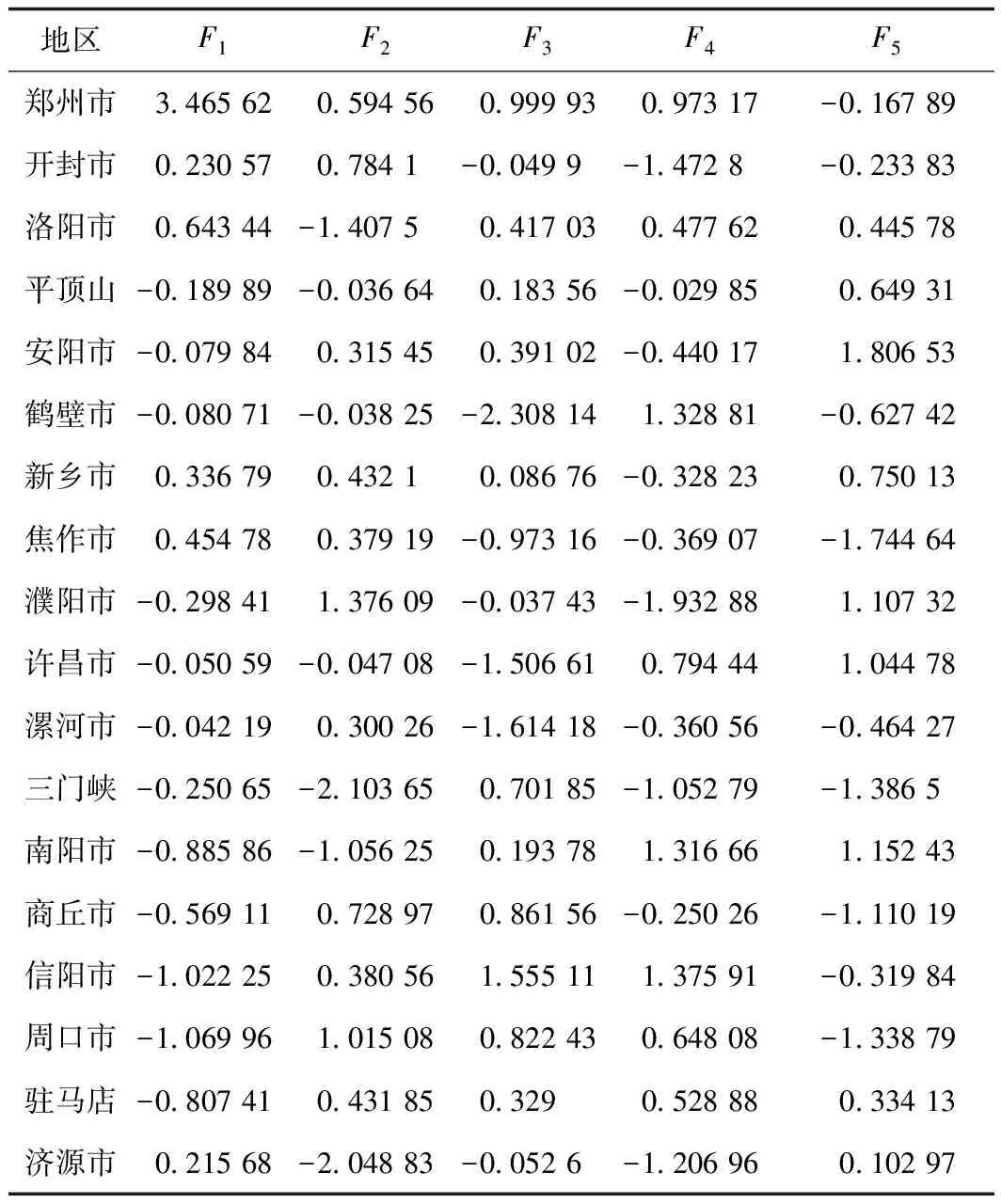
表4 样本的主成分得分表Tab.4 Score of principal component of the samples

2.3 改进TOPSIS法评价过程

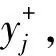
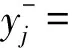
-1.74464]

根据公式(4)、(5)计算每一个样本与正、负理想解的加权距离D+、D-，其中权重来源于个主成分指标的方差贡献率51.631%、14.558%、9.634%、7.525%、5.481%，对其进行归一化后得到权重：

wj=[0.581242 0.163885 0.108455 0.0847120.061706]

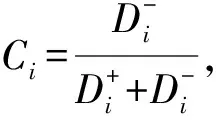
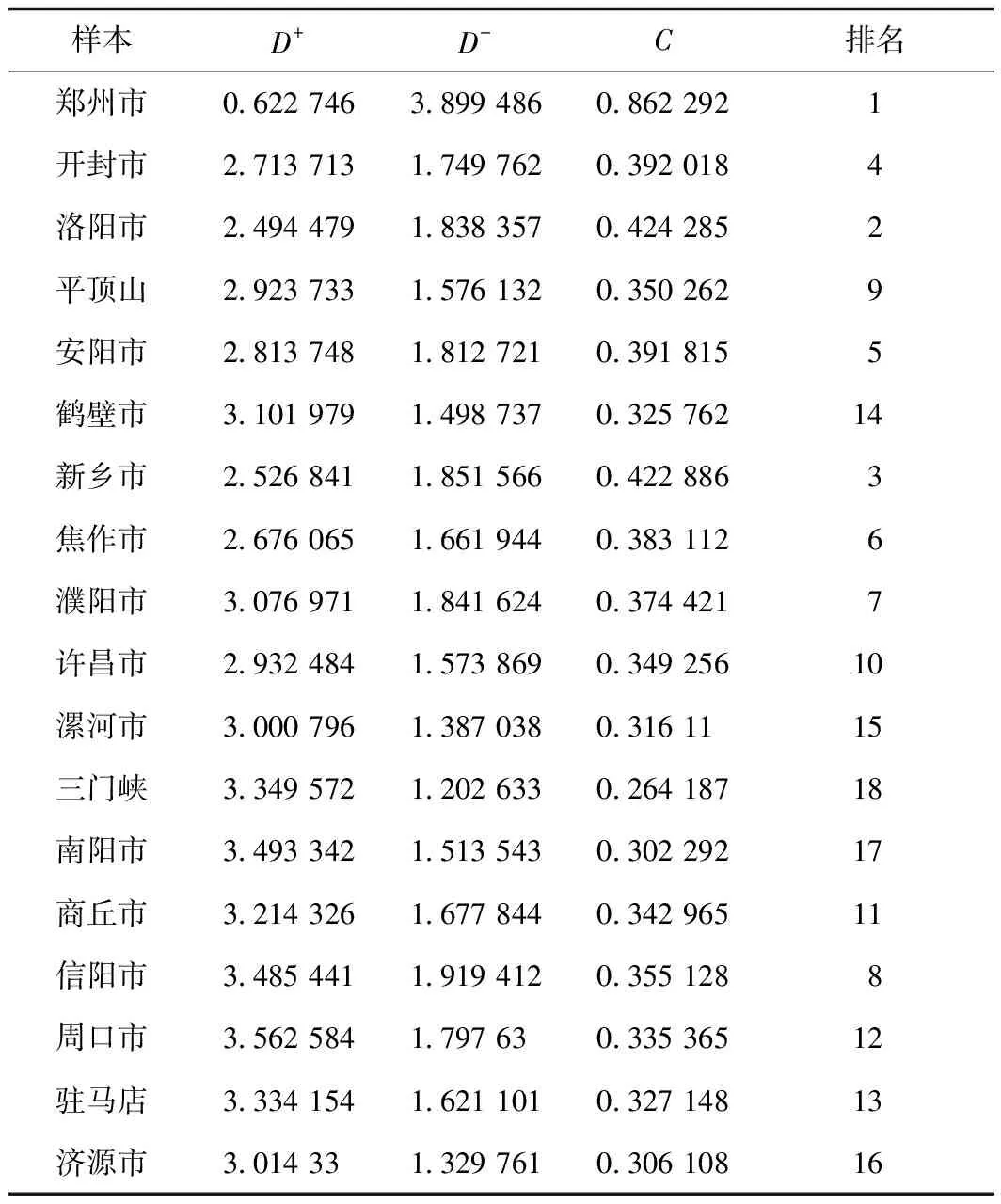
表5 各评价对象到正、负理想解距离及排序表Tab.5 Distance between each evaluation object, and positive and negative ideal solution and rank table

根据表5，绘制河南省各市社会发展水平柱形图如下：

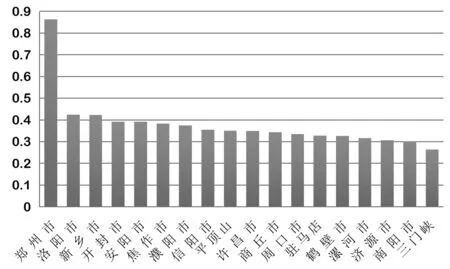
图1 河南省各市社会发展水平图Fig.1 Social development level of all cities in Henan Province

3 结论与建议

从图1可知，河南省各市的社会发展水平最高的是郑州，且远远高于其他市县，为0.862 292；三门峡最低，为0.264 187；而洛阳、新乡、开封、安阳等处于郑州周边的城市得分接近，排名比较靠前；漯河、济源、南阳等远离东部发达地区的城市排名则相对靠后。如此可以看出，河南省各市社会发展呈现出“一城独大”的特征，省会城市郑州的综合得分要远超其他各市。从地理位置上看，郑州及以郑州为中心的周边城市的发展水平要稍稍高于其他城市的发展水平。除郑州外，其他各市县发展优势点各有不同，综合水平相差较小。由主成分指标数据可知，综合的社会发展水平不仅受经济发展的影响，同时依赖于其他多方面因素的快速发展，如农村现代化水平、科技与教育水平等。南阳是河南省人口第二、面积最大的城市，也是中部地区重要的交通枢纽、国家历史文化名城，其经济实力处于省内前三。但作为人口大市，其研究生培养单位只有一所，本科院校仅有三所，落后的教育水平不能与其经济发展相匹配，人均可支配收入、医疗机构床位数等也处于末位，这使得其排名很靠后。

针对河南省社会发展特点，提出如下建议：其一，政府可以根据主成分指标值的大小，明确各地的优缺点，因地制宜，制定适合当地发展的经济政治策略。其二，发挥中心城市的引领示范作用。郑州和洛阳作为省会城市和中心城市，要发挥带头作用，分享经验，带动周边城市的发展。其三，加大力度，扶持落后地区。三门峡位于河南省最西边，东临洛阳，西望西安，毗邻两大古都，是历史上三省交界的文化中心，并拥有丰富的矿产资源。但三门峡市经济发展比较落后，所以其发展的重点是要依托文化、资源、生态优势，带动经济发展，从而提高人的生活质量，促进社会发展。其四，保证地区的各方面协调发展。在大力发展经济的同时，也要注意科技教育、人民生活、社会保障及各地区特色产业等方面的均衡协调发展，只有社会发展的各个方面协调并进，各个地区均衡发展，才能构建一个满足人民生活需要、可持续发展的社会。