航班扰动情形下的飞机路线恢复研究

魏依凝， 吴永强， 曾 实

(中国民用航空飞行学院 机场工程与运输管理学院， 机场管理与工程研究中心， 四川 广汉 618307)

随着中国经济总量持续增长，居民收入稳步增加，越来越多的旅客选择航空方式出行。然而面对有限的资源、恶劣天气、空中交通流量管制以及飞机停场等情况，导致无法执行原航班计划，造成航班计划的扰动(perturbation)。

航班计划受扰后，若延误航班未及时恢复，则会将延误传播到与其有关的所有下游航班，产生“延误波及”现象。2016年，民航大数据研究院曾对航班延误波及问题做了相关研究[1]，对于一天内有4次航班任务的飞机而言，当飞机执行第一航班时，起飞延误率仅为26.06%；可到了第四航班起飞时，延误率已达49.14%。若是国际航班产生延误波及，甚至可能会严重影响中国在整个航空业的声誉。2015—2019年，中国主要航空公司平均每年执行航班300.2万班次，其中正常航班227.86万班次，平均每年航班正常率为75.9%，与“十三五”时期民航发展预期的“80%航班正常率”[2]有一定距离。当航班计划发生扰动时，以中国一架延误的空客333飞机为例，其延误费用可达到10万以上。因此快速获取有效的航班计划恢复方案，减少航空公司损失十分重要，并且飞机是航空公司的宝贵资源，飞机路线的恢复尤为关键。

国内外学者针对恢复飞机路线的问题进行了相关研究。Yan等[3]提出了一个基本调度扰动模型(basic schedule perturbation model，BSPM)，使用拉格朗日松弛法和次梯度法求解；Yan等[4]拓展其研究，将BSPM模型扩展为基本的多机型调度扰动模型，以同样的算法求解，运用案例验证了模型的可行性。Bard等[5]利用节点和弧为每架飞机构建了时空网络，并在此基础上提出了以航班延迟和航班取消成本之和最小为目标函数的数学模型，解决了单机型的飞机恢复问题；Thengvall等[6]提出了3个多商品网络流模型解决飞机恢复问题，并分别比较3种模型解的质量和计算时间，得出第一种模型给出的飞机恢复方案较为出色；Nickkar等[7]针对航班扰动恢复，提出了一种基于非线性规划的多目标优化模型，采用了Dantzig-Wolfe分解算法求解，模型可解决大规模航班恢复问题；Zhang[8]提出了用两阶段启发式算法来降低航班恢复问题的规模，设计了飞机恢复模型；赵秀丽等[9]建立了以延迟成本或延迟时间最小为目标函数的航班恢复模型，能在较短CPU时间内给出恢复方案；白凤等[10]建立了以航班延迟成本和取消成本之和最小为目标函数的多商品网络流数学模型，使用列生成算法求解，算例验证了模型的正确性；朱星辉等[11]将机型指派和飞机路线一体考虑，提出了多机型的一体化飞机排班多商品网络流模型，用一种基于约束编程的动态列生成算法求解此模型，实验结果证明了模型和算法的有效性；张力菠等[12]在航班延迟和航班取消这两种基本策略上加入摆渡飞机策略并建立了以恢复成本最小为目标函数的数学模型，实例验证了模型的有效性。乐美龙等[13]改进了时空网络，提出了多机型不正常航班恢复模型，算例表明多机型航班恢复模型给出的方案优于单机型航班恢复的方案。

综合来看，飞机路线恢复问题的文献成果较为充足，特别是单机型的航班扰动恢复的研究较为丰富，但多机型的航班扰动恢复的研究较少；且在考虑恢复策略方面，大多数只考虑了延迟航班和取消航班两种策略，同时考虑延迟航班、取消航班、替换飞机和摆渡闲置飞机的情况较少。因此，基于已有文献，本文将在机场临时关闭和飞机停场的情况下，同时考虑以上4种策略，改进经典的离散时空网络，并以此建立多机型飞机路线恢复模型，用算例验证模型的可行性。

1 航班扰动情形分析

在现实生活中，经常会碰见沙尘暴、大雪和台风等极端天气，导致能见度骤降、跑道摩擦系数不够起降标准，迫使机场关闭；此外，机场活动区有异物、军事演练和空中交通流量控制等人为因素同样也会使机场关闭，只能延迟或取消受影响的航班。对有执行计划航班的飞机来说，出发机场关闭和到达机场关闭是不同的两种情况，所以本文将分别讨论这两种情况。

除了机场临时关闭这种情形，若是机务故障或其他意外事故造成某飞机临时丧失适航性造成飞机资源不足，不能执行原计划飞行任务的情形称为飞机停场(grounding)[14]。显然，飞机停场也会引起航班计划的扰动，这是需要考虑的第二种情形。

1.1 机场临时关闭

如图1所示，现分别假设两种情况，情况1：由于台风的影响，SHA、SZX这两个出发机场需在12：30—15:00临时关闭，在此期间起飞的航班需要在15:00之后机场再次开启才能继续执行；情况2：由于受大雪影响，PEK机场需在15:00—18:00临时关闭，则在此期间到达PEK机场的航班需要在18:00之后才能降落。

图1(a)为情况1的简化时空网络图，节点1和节点2分别代表航班1的出发机场和到达机场以及各自的出发、到达时间，连接两点形成的实线为航班1的原计划路线12，路线34即是航班2的原计划路线，由于机场在15:00之后才开启，航班的出发时间需延后至节点1′和节点3′所在的15:00，航班1和航班2延后的到达时间节点分别为节点2′和节点4′，两航班的新路线由图中虚线所示，分别为1′2′和3′4′，图中的t1和t2分别为航班1和航班2的延迟时间，可计算各自航班延迟成本Delaycostf(t)，f为航班号，t为延迟时间。为使网络更简单，减少建模的难度和求解时间，以航班1为例，在航班延迟后，不生成节点1′，而连接节点1和节点2′，形成的新路线12′由点划线所示，在12′中计算航班1的延迟成本。

图1(b)所示是情况2的简化时空网络图，由于PEK机场再次开启时间为18:00，所以航班1和航班2需要各自延迟t3和t4时间，到图中的节点4′处，路线12和路线34代表原计划航班路线，路线1′4′和路线3′4′代表延迟后航班执行路线，同样不生成节点1′和节点3′，在路线14′和路线34′中计算各自航班的延迟成本Delaycostf(t)。

图1 出发机场临时关闭和到达机场临时关闭

1.2 飞机停场

如图2所示，现假设A320型飞机1临时出现故障，当天无法修复，面对此种情形，有3种处理方法，一是取消航班3，二是选择摆渡其他机场刚好闲置的A320型飞机到所需机场，三是选择同机场的A321型飞机进行飞机替换，但需注意为了使替换飞机能有执行航班的可能性，A321型飞机执行航班时间不得晚于A320型飞机执行航班时间。

图2的左图和右图分别是A320型飞机1和A321型飞机1的简化时空网络图，由于A320发生故障且在当天无法恢复，PEK机场有一架闲置的A320型飞机在节点0处，可供航班3使用，航班边-3和航班边-4分别表示航班3和航班4，连接节点0和节点1形成摆渡边-3，摆渡A320型飞机的费用可在摆渡边中计算Ferrycostp(t)得到，p为摆渡飞机，t为摆渡飞机到所需机场的时间。除了摆渡飞机执行航班3以外，还可以采用飞机替换策略，利用同在SZX机场的A321型飞机1来执行航班3，连接节点1和节点3形成替换边-3，替换飞机A321的费用可在替换边中计算Substitutioncostf(u)得到，f为航班号，u为乘客人数。若A321型飞机1去执行了航班3，无法准时执行航班4，摆渡飞机、替换飞机的处理方法同航班3。

图2 A320(左)和A321(右)双机型简化时空网络图

2 离散时空网络的构建

经典离散时空网络由节点和有向边构成，用二维坐标系呈现，能够很好地描述飞机在时间和空间位置上的变化。其中，横坐标用离散的点标注机场代码来代表各个机场，纵坐标代表时间，纵坐标的起点和终点分别代表受扰航班进行恢复的开始时间和受扰航班恢复的结束时间，若将时间离散化，则可得到若干个时间节点，这样的节点可显示具体的时间和空间位置。时空网络中有3类节点：源节点、机场时间节点和沉没节点；3类有向边：航班边、复制边和沉没边；为避免网络复杂后不方便查阅，一般省去各类边的箭头。以上3类节点和3类有向边可较好地描述延迟航班、取消航班策略，但若是要考虑摆渡飞机和替换飞机策略，运用经典的离散时空网络是无法体现的，需增加摆渡边和替换边。

首先分析实际情况，获取受扰航班的恢复时期，可用飞机资源情况，包含闲置飞机所在机场和可用时间，根据原始航班计划，确定离散时间区间大小，建立可用飞机的机场时间节点，闲置飞机从所在机场摆渡至其他机场所形成的边为摆渡边，对有可能达到的机场形成新的可用机场时间节点，然后在机场时间节点基础上生成航班边、复制边、沉没边，最后将每个机场的孤立节点融合为一个节点，形成各机场的沉没节点，输出最终单机型离散时空网络。若是有多余的机型资源可供进行飞机替换策略，注意这样替换是发生在同一个机场内的，先依照同样的方法生成替换飞机的离散时空网络，然后将替换机型的各机场时间节点与被替换机型的各机场时间节点用替换边依次连接，且被替换机型的各机场时间节点的时间要相同或较晚于替换机型的各机场时间节点的时间，这样才能发生替换，产生替换边，形成多机型离散时空网络。改进后的简化离散时空网络可详见图3。

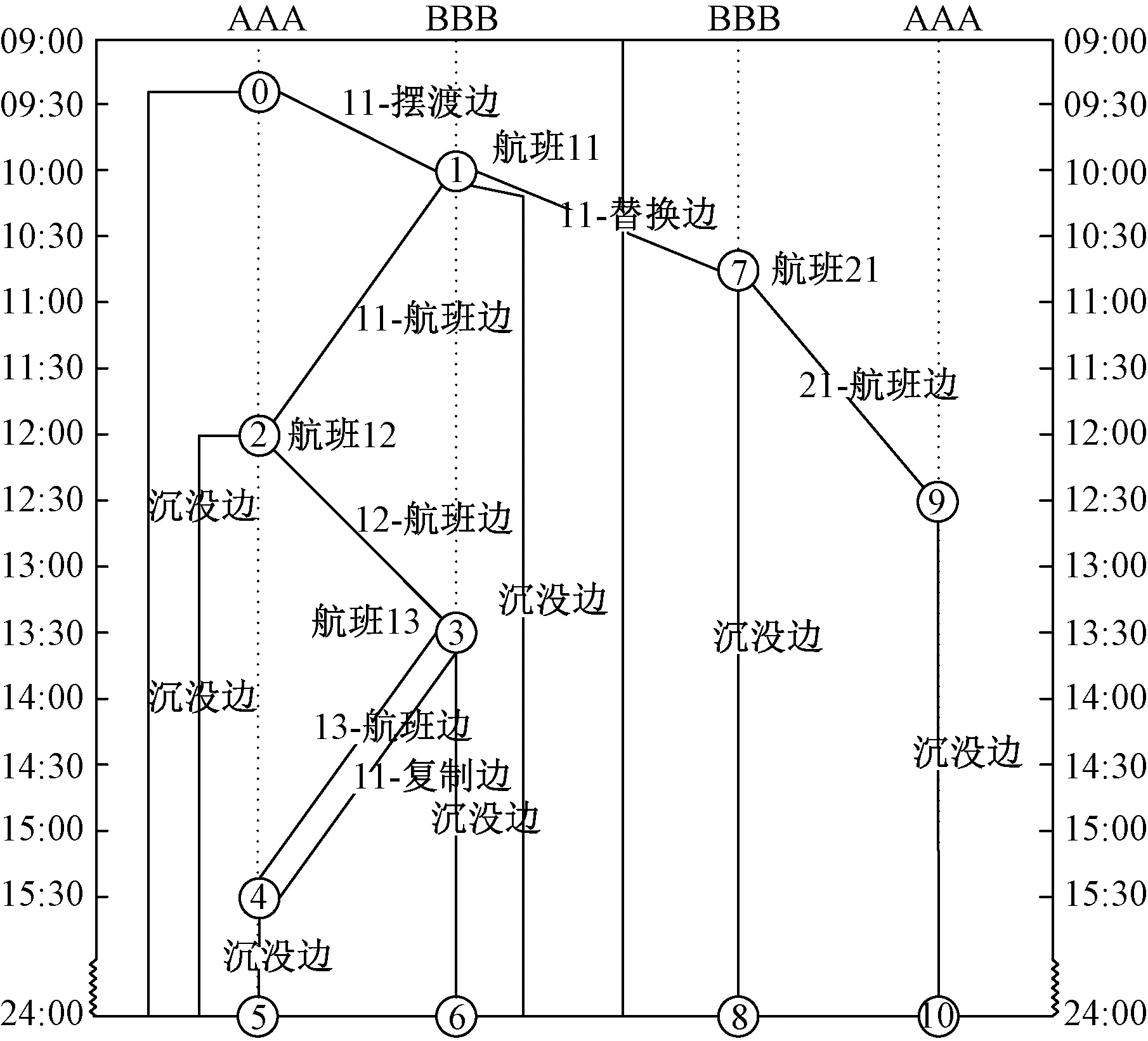
图3 改进后的双机型离散时空网络

3 数学模型

文献[12]在建立不正常航班调度模型时，只考虑了单机型的延迟航班、取消航班和摆渡飞机，没有考虑多机型的替换；而文献[13]虽考虑了多机型的替换，但忽略了摆渡飞机这个策略，并且也没有考虑到机场关闭这种情形。所以基于以上两篇文献模型的优缺点以及第2节中改进后的双机型离散时空网络图，定义以下索引、集合、参数和变量。

1)索引：i、j为节点索引；p为摆渡飞机索引；r为飞机替换边索引；k为航班索引；b为摆渡边索引；q为沉没边索引；f为航班边索引；e为机型索引。

2)集合：T为机场时间节点集合；G为机场沉没节点集合；F为航班集合；A为航班边集合；Q为沉没边集合；A(k)为航班k的航班边集合；P为摆渡飞机集合；B为摆渡边集合；E为机型集合；R为飞机替换边集合；B(p)为飞机p的摆渡边集合；C(i)为节点i的摆渡边集合；S(i,e)为机型e执行的从点i出发的航班边集合；U(i,e)为机型e执行的终点为i的航班边集合。

5)目标函数：

(1)

6)约束条件：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

4 飞机路线生成算法

求解上述模型后，可得到最优执行的替换边、摆渡边和航班边集合，通过替换边可知飞机发生了替换；通过摆渡边，可知将闲置飞机摆渡至哪一个机场可使成本最优，但对于航班边，只能得到优于执行的航班，却不知这些航班由哪一架飞机执飞。因此对于求解后的航班边集合，需进行飞机指派，算法在文献[15]基础上进行改进，增加飞机替换策略，解决飞机指派问题，生成飞机路线。

算法1 飞机路线的生成

input:O={根据模型求解出来的最优执行的航班边集合}、R={根据模型求解出来的最优执行的替换边集合}、A={可用飞机(包含闲置飞机)}

output:Z={可用飞机和它们所执行的航班}

begin

for each在A中的飞机a do

begin

创建一个元素n，以飞机a的尾号、可用时间、当前所在机场来标记元素n，将元素n放入Z中

end

非降序排列Z中的飞机可用时间

非降序排列O中的航班标记的出发时间和原计划出发时间

while当O不为空 do

begin

从O中移出第一个元素o

if 元素o所代表的航班边的时间节点上没有最优执行的替换边rthen

从Z中搜寻位于航班o出发机场的第一架可用飞机n，将n指派给o

else 飞机n根据替换边r指派给o

更新飞机n的可用时间和当前机场，将Z再次排序

end

end

5 算例分析

表1来自于北京某航空公司空客A321-200型飞机和空客A320-200型飞机的部分航班计划，也是本文的算例数据，涉及8架飞机、32个航班和4个机场(深圳宝安国际机场、上海虹桥国际机场、北京首都国际机场和成都双流国际机场)，各个航班的取消成本由Cf=mfwfsf计算而来，其中Cf为航班f的取消成本；mf为航班f最大载客人数；wf为航班f的平均票价水平；sf为航班f的客座率。

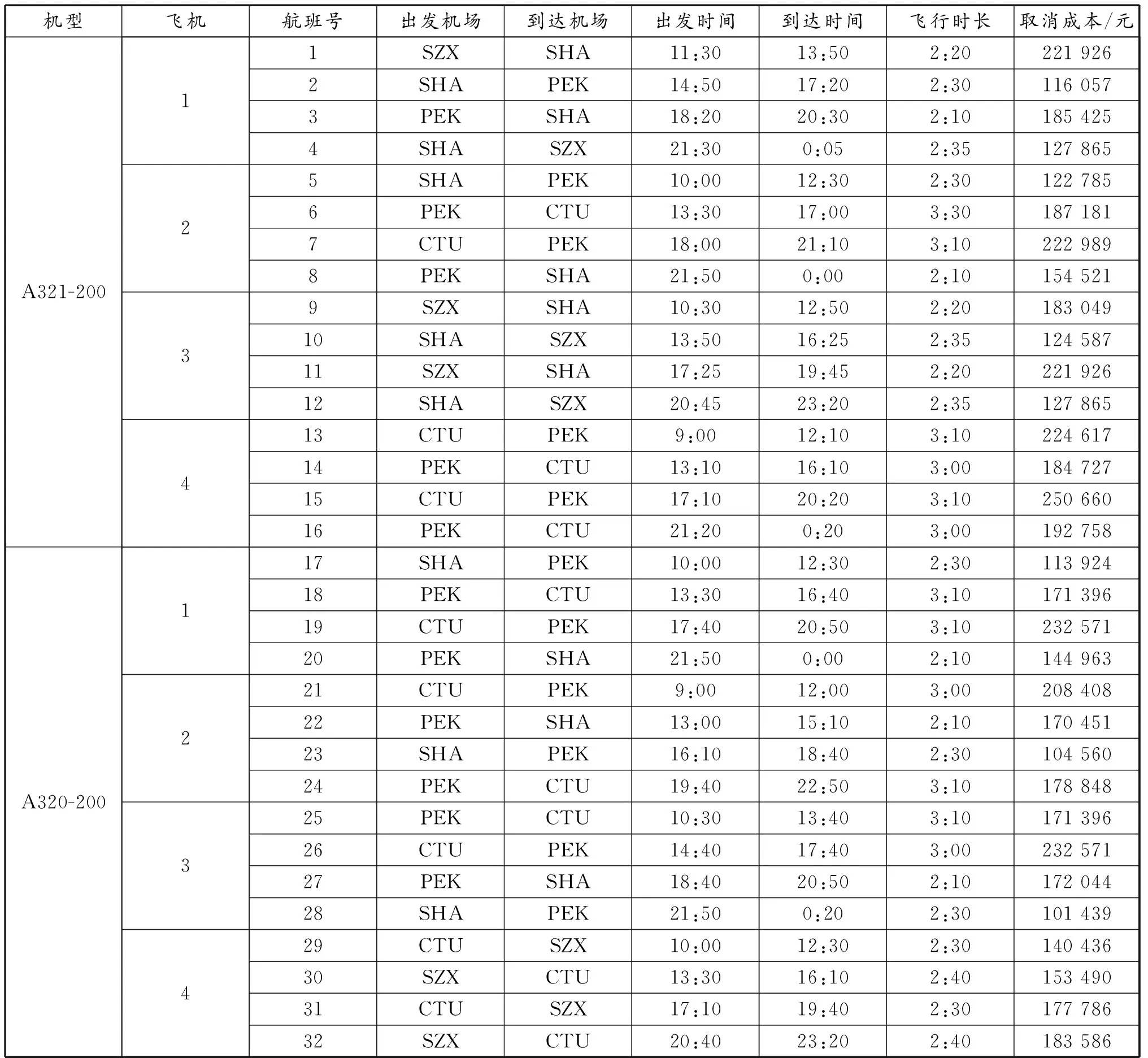
表1 321-200和A320-200的原航班计划

现在原航班计划执行前，发生以下航班扰动情形：受台风影响，SHA机场将在17:30-20:00关闭，则受影响的有到达SHA机场的航班11和从SHA机场出发的航班12，A321-200中的飞机2和飞机4以及A320-200中的飞机3临时出现故障，且当天都不可用， SZX机场有一架闲置的A321-200飞机可供摆渡到SHA机场、PEK机场、CTU机场，飞机的摆渡信息见表2，同时这两机型飞机可发生飞机替换，飞机替换成本包含发生替换的机场产生的设备及人工成本和替换后飞机空间大小的改变引起乘客的心理反感成本，但这项成本只会发生在大机型被替换为小机型的情况下计算，反之则不用计算这一成本。这里引用文献[13]采用的1 000元/人和50元/人进行计算，航班延迟成本以197元/min[16]计算。

表2 A321-200的摆渡信息

A320机型、A321机型在第一类机场的最少过站时间为60 min，取30 min为离散时间的间隔，以第2节的方法建立考虑了以上策略后的A321-200和A320-200的双机型离散时空网络，具体可见图4。节点0处有一架闲置在SZX机场的A321-200飞机，虚线代表摆渡边，共3条；点划线代表替换边，共173条。为避免时空网络图过于复杂，影响读者阅读，只在图中画出了34条替换边，省略139条替换边。

基于图4，使用CPLEX优化软件求解模型，表3为考虑航班延迟、取消、摆渡飞机和飞机替换这4种恢复策略的结果，飞机摆渡至SHA机场，A320-200型飞机2替换A321-200型飞机4执飞航班14和航班15，共取消航班8个航班，延迟6个航班，总恢复成本为1 435 409元。

表3 A321-200和A320-200的航班计划恢复表

图4 A321-200和A320-200的双机型离散时空网络

以上的飞机路线恢复同时考虑了①取消航班、②延迟航班、③摆渡飞机、④替换飞机4种策略，但也可能出现没有闲置飞机可供摆渡以及机型不能发生替换的情况，所以总体来说有4种恢复方案，方案1为直接取消受影响航班；方案2考虑取消和延迟受影响的航班；方案3在方案2的基础上加入摆渡飞机策略；方案4是综合考虑取消航班、延迟航班、摆渡飞机和替换飞机4种策略，表4展示了4种恢复策略选取组合后的方案结果比较。

表4 4种恢复方案的比较

对比以上4个恢复方案的飞机路线恢复成本，同时考虑延迟航班、取消航班、摆渡飞机和替换飞机的方案4为最优恢复方案，与方案1、方案2、方案3相比分别减少了782 279元、736 063元、35 314元，结果优化分别达到35.27%、33.90%、2.40%。

6 结语

主要针对在机场临时关闭和飞机停场两种航班受扰情形下，考虑同时采取延迟航班、取消航班、摆渡闲置飞机和飞机替换策略，在经典离散时空网络的基础上增加摆渡边和替换边表达以上4种策略，以此建立了受扰航班飞机路线恢复成本最小模型。运用算例数据，使用CPLEX优化软件进行求解，给出了较优的航班恢复计划。对比了4种恢复方案的结果表明，同时采取4种策略进行飞机路线恢复为最优方案，验证了模型的可行性。但是，本文没有考虑机场时刻容量的约束，且飞机恢复结束时间截至当日，在飞机恢复后，未对后续机组人员和乘客的恢复进行考虑，在未来，这些也是本文需更深一步研究的方向。