基于脉冲涡流的提离高度检测方法

殷雪峰，程千里，窦凤杰，崔建杰

(1.中国石化 青岛炼油化工有限责任公司，山东青岛 266500；2.天津特米斯科技有限公司，天津 300131)

0 引言

利用脉冲涡流(Pulsed Eddy Current,PEC)检测技术对带保温层的金属管道或设备壁厚进行检测，是近几年发展起来的一种新型非接触式无损检测技术。与传统涡流检测技术不同，脉冲涡流检测技术采用方波作为激励方式，激励能量更强，具有很好的穿透性能，能够穿透几十甚至上百毫米的包覆层(保温层和保护层)，可真正实现在不拆除保温层的情况下对承压管道或设备的不停机检测，该技术已在炼油化工等行业中得到了广泛应用[1]。

现有利用脉冲涡流检测技术对带保温层的铁磁性材料壁厚进行检测，一般采用拐点时间[2-3]或晚期信号衰减率(或称晚期信号斜率)[4-8]作为特征值，其中，拐点时间受提离高度影响较大[2-3]，晚期信号衰减率受提离高度影响较小[8]。目前，为抑制脉冲涡流检测信号的提离效应，测量提离高度已经成为脉冲涡流检测技术的研究热点[9-14]。在工程应用中，需要根据提离高度选择合适的脉冲涡流传感器和相关参数(发射电压、发射频率等)。如参数选择不当，可能引起壁厚检测数据的偏离，甚至不能得到壁厚值，造成管道壁厚检测的漏检或误检。因此，获得提离高度的准确值，对提高带保温层管道或设备壁厚检测的准确性有重要意义。

本文对铁磁性材料脉冲涡流的信号特点进行分析，提出以脉冲涡流中期信号截距作为特征量进行提离高度测量的方法，并进行试验验证。

1 脉冲涡流信号特点分析

脉冲涡流检测技术属于涡流检测技术(Eddy Current Testing，ECT)的一个分支，其基本原理是在线圈中通入恒定电流或电压，在一定时间内，被测构件中会产生稳定的磁场，当断开输入时，线圈周围会产生电磁场，该电磁场由直接从线圈中耦合出的一次电磁场和构件中感应出的涡流场产生的二次电磁场两部分叠加而成，且后者包含了构件本身的厚度或缺陷等信息，采取合适的方法和检测元件对二次场进行测量，分析测量信号，即可得到被测构件信息[1]。

脉冲涡流早期感应电压信号幅值大、衰减快，中晚期信号幅值小且衰减相对较慢，信号动态范围大，不同壁厚的脉冲涡流信号在笛卡尔直角坐标系中几乎重合在一起，如图1所示，故在直角坐标系中无法对脉冲涡流信号特点进行分析。如将时间信号和感应电压信号都进行对数转换，在双对数坐标系(lnV-lnt坐标系)或单对数坐标系(lnV-t坐标系)中，脉冲涡流信号的特征都能清晰地显示，如图2～4所示。

从图2可以看出，在双对数坐标系中，不同壁厚构件的感应电压信号在中期阶段基本重合且表现为直线段，可理解为在中期阶段感应电压信号的衰减规律符合幂函数衰减规律。随着衰减时间增加，感应电压信号衰减速度增加，在图2中表现为感应电压信号曲线向内弯曲，且被测构件壁厚越薄，感应电压信号曲线弯曲段出现越早，反之亦然。在双对数坐标系中，感应电压曲线由直线段到曲线段的过渡时间称为拐点时间，可作为壁厚检测的特征值[2-3]。

从图3可以看出，在单对数坐标系中，感应电压信号曲线中期阶段基本重合且表现为弯曲段，后期阶段感应电压曲线趋向于直线段，可理解为在后期阶段感应电压信号的衰减规律符合指数衰减规律。在该阶段，被测构件的厚度对感应电压曲线的影响表现为曲线斜率的变化，壁厚越小，直线段曲线斜率的绝对值越大，反之亦然。在单对数坐标系中，感应电压曲线晚期阶段的斜率(或称为晚期信号衰减率)也可作为壁厚检测的特征值[4-8]。

从图4可以看出，在双对数坐标系中，当提离高度相同时，不同壁厚被测构件的感应电压信号曲线在中期阶段基本重合；当提离高度不同时，相同壁厚被测构件的感应电压曲线在中期阶段不同。

综合以上分析，可得到如下结论：

(1)感应电压信号中期阶段符合幂函数衰减规律，晚期阶段符合指数函数衰减规律；

(2)提离高度相同时，不同壁厚被测构件的感应电压信号曲线中期阶段基本重合，感应电压曲线中期阶段不受壁厚影响；

(3)提离高度不同时，相同壁厚被测构件感应电压信号曲线不同，感应电压曲线中期阶段受提离影响。

以上结论与文献[15-17]中内容基本一致。如文献[15]将脉冲涡流信号划分为3个阶段，其中第Ⅰ阶段对应着激励线圈中矩形波电流的下降沿阶段，即电流从矩形波幅值的90%下降至10%的阶段，其持续时间一般为ms数量级，该阶段的感应电压信号为一次磁场和二次磁场共同作用的结果，从中难以提取出被检件信息。第Ⅱ阶段始于矩形波电流的下降沿结束时刻tⅡ，一直持续到涡流密度最大值转移至被检件厚度一半深度处的时刻tⅢ。在此之后，涡流在被检件中仅向外扩散和衰减，直至完全耗散的过程对应着PEC 信号的第Ⅲ阶段。文中所提中期阶段对应上述文献的第Ⅱ阶段，晚期阶段对应上述文献中的第Ⅲ阶段。

文献[15]中列出了第Ⅱ,Ⅲ阶段脉冲涡流信号V(t)的分段函数：

(1)

式中,FⅡ(l)为与提离高度l相关的函数;δ为试件的电导率;tⅢ为二次磁场到达被测构件下底面的时间;FⅢ(l,d)为与提离高度l和被测构件壁厚d相关的函数；c为常数;μ为试件的磁导率。

2 基于中期信号截距的提离高度检测方法

对于铁磁性材料而言，感应电压信号随时间衰减可以分为幂函数衰减阶段和指数衰减函数衰减阶段，其中幂函数衰减阶段为信号的中期阶段，其感应电压信号与被测构件厚度无关，而与被测构件的材料特性和提离高度相关。在被测构件材质相同的情况下，幂函数衰减阶段的中期信号只与提离高度相关，若能找到中期感应电压信号与提离高度的特征关系，就可通过中期感应电压信号求得提离高度。

2.1 提离高度特征值的确定

对式(1)第二阶段分段函数两边取对数，可得：

(2)

对于同一材质的被测构件来说，δ和μ为常数，可将ln[FⅡ(l)δ1/2μ1/2]简化为G(l),同时，为便于分析，将ln[V(t)] 设为Y，将lnt设为X，则式(2)可以简化为：

Y=-1.5X+G(l)

(3)

式(3)中，G(l)为与提离高度相关的函数，且在双对数坐标系中为感应电压中期信号的截距。因此，可以将双对数坐标系的中期信号截距作为提离高度的特征值。

2.2 利用截距计算提离高度的方法

通过以上分析，可得到利用脉冲涡流中期信号幂函数衰减阶段在双对数坐标系中的截距计算提离高度的方法。

(1)提取双对数坐标系下被测构件若干不同提离高度的感应电压曲线中期信号的截距ki。

(2)根据已知提离高度li和中期信号截距ki的对应关系，通过拟合得到函数l(k)的关系式。

(3)取相同材料被测构件任意区域的脉冲涡流信号，提取双对数坐标系中期信号截距k，根据l(k),即可计算出被测构件指定区域的提离高度。

3 利用截距检测提离高度的试验验证

为对上述方法进行验证，采用TEM-PFSS-II脉冲涡流检测仪对不同提离高度的试验样管进行试验。试验保温层为聚氨酯类保温层；保温层上保护层为铝皮，厚度约为0.4 mm。试验用探头为保温探头，主要参数：发射线圈内径10 mm，外径75 mm，高度40 mm，匝数1 200匝；接收线圈的内径75 mm，外径85 mm，匝数1 600匝。发射信号选择频率4 Hz、占空比为50%的方波电流；取电流关断时刻为感应电压信号的采集起始点。

3.1 截距与提离高度拟合方程的获得

取壁厚为4，6，8，12，16 mm、材料为20#碳钢的标准样板，在提离高度分别为5，10，20，30，40 mm的情况下进行检测，提取各壁厚和提离高度下感应电压信号在双对数坐标系中的中期信号截距值，将截距值列入表1中。按照第2.2节中所述方法，以截距ki为横坐标，以提离高度li为纵坐标，并用幂函数对{(ki,li)}进行拟合，可得到不同壁厚情况下提离高度与截距值的拟合曲线，如图5所示。

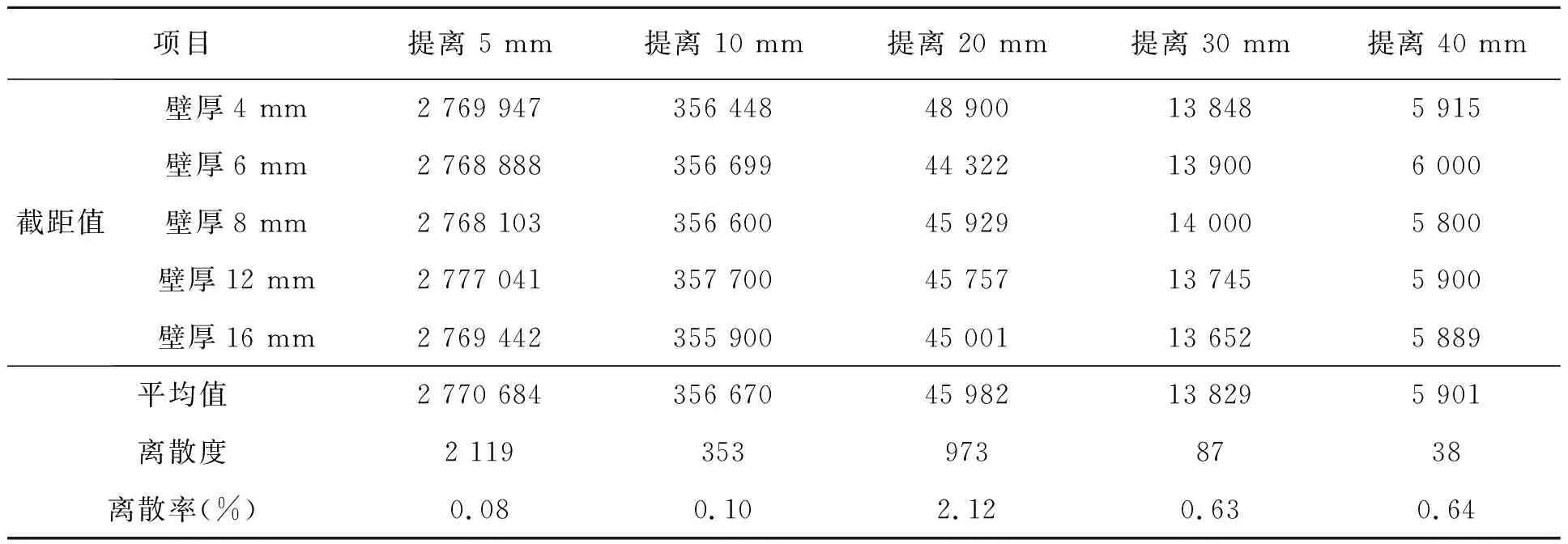
表1 不同壁厚、不同提离高度下的中期信号截距值

分析表1和图5的数据可以得到如下结论。

(1)当提离高度相同时，被测构件壁厚不会对截距值产生影响，即被测构件厚度不影响提离高度的测量。

(2)当被测构件的壁厚相同时，测得的截距随壁厚值增加而减小，当采用幂函数拟合时，5个壁厚值的拟合曲线基本重合，且拟合效果较好。

(3)根据以上数据可以得到提离高度与截距之间的方程：l=753.27k-0.338,该方程不受被测构件壁厚的影响。

3.2 试验管提离高度的验证试验

试验管材料为20#碳钢，外径273 mm，壁厚8 mm。保温层厚度分别为25，50，75，100 mm,且保温层上覆盖厚度为0.4 mm的铝皮作为保护层。

针对不同提离高度，采用不同发射电压进行测量，在获取双对数坐标系中期信号截距后，对不同电压下的截距，按公式l=753.27k-0.338计算出被测位置的提离高度，并与实际的提离高度进行比较，结果如表2所示。需要注意的是，虽然铝皮具有一定厚度，但其与保温层相比，厚度较小，因此实际提离高度未将铝皮厚度考虑在内。

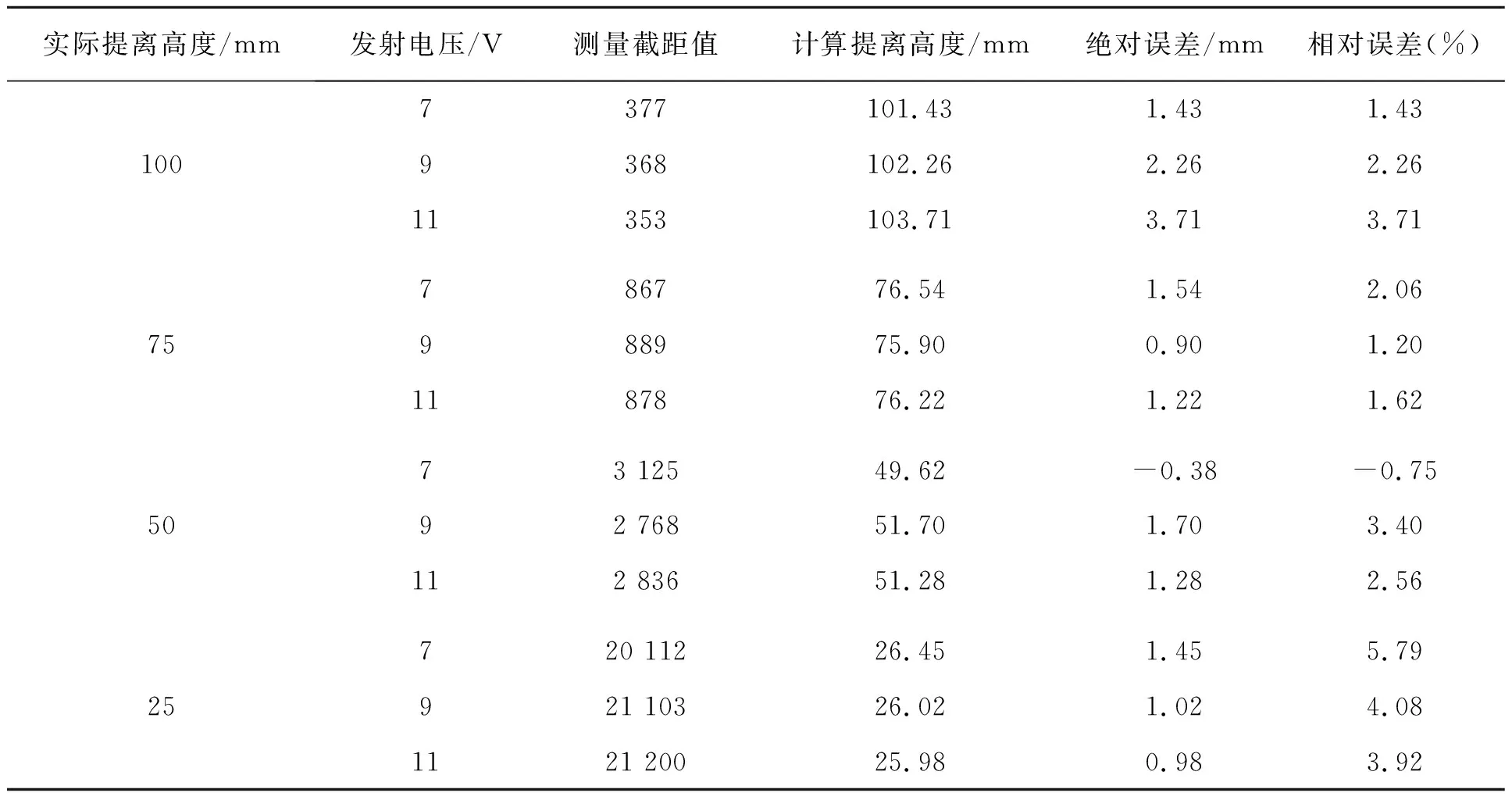
表2 试验数据

由表2数据可知，当提离高度在100 mm以内时，利用双对数坐标系中直线段(脉冲涡流信号幂函数衰减阶段)的截距作为脉冲涡流检测中提离高度测量的特征值，计算得到的提离高度与实际提离高度值比较接近，相对误差基本可以控制在5%以内，效果较为理想；且该方法不受发射电压(或电流)和铝皮厚度的影响。

4 结论

通过分析脉冲涡流检测信号，提出在双对数坐标系中，利用中期信号截距作为提离高度测量的特征值，并通过不同提离高度特征值拟合出提离高度和中期信号截距之间的关系式。通过试验验证，该方法具有一定的准确性，在保温层厚度不大于100 mm的情况下，其相对误差基本未超过5%，且该方法不受被测构件厚度和发射电压的影响，具有较好的应用性。该方法解决了带保温层管道或设备中保温层厚度的测量方法，扩充了脉冲涡流检测技术的应用范围，有利于提高利用脉冲涡流检测技术穿透保温层检测管道或设备壁厚的准确性。