基于VMD-ISD的天然气管道泄漏信号去噪研究

王冬梅，肖超利，路敬祎,2

(1.东北石油大学 电气信息工程学院,黑龙江大庆 163318；2.黑龙江省网络化与智能控制重点实验室，黑龙江大庆 163318)

0 引言

管道运输因易于管理，运维成本低等优势，被广泛应用于石油天然气等重要化工原料的运输[1]。但管道面临复杂的地质条件，容易造成管道材料的锈蚀，而且人为破坏、盗取行为容易引起重大的管道泄漏事故[2]。为减少管道泄漏造成巨大的经济损失及危害，国内外对管道泄漏检测技术[3-5]进行了大量研究。国际上常见的输运管道泄漏检测方法有声波法、人工检测法、压力梯度法和光纤检测法等，但是传感器采集到的管道泄漏信号往往存在压缩机振动、人声等大量外界环境产生的噪声，并对检测效果产生一定的影响，因此需要对管道泄漏信号进行预处理，以减少噪声对检测结果的影响。管道泄漏信号是一种典型的非线性非平稳信号。对此信号常见的分析方法有小波变换[6](Wavelet transform,WT)、经验模态分解[7](Empirical Mode Decomposition,EMD)和变分模态分解 (Variational Mode Decomposition,VMD)算法[8-9]等。WT在分析非线性非平稳信号时，可以满足时频信号的分析要求，解决了傅里叶变换的难点，但WT存在小波基和分解层数难以确定的缺点。EMD无需预先确定小波基函数和分解层数，具有很好的自适应性，但存在模态混叠和端点效应等缺点[10]。VMD算法可根据实际信号的频段分布，人为设定分解的模态数量K值，并以设定的带宽和迭代方式获得中心频率，进而获得模态函数，有效地避免了EMD存在的模态混叠问题，并在采样和去噪方面具有很好的鲁棒性。但若人为设定K值，不准确会严重影响VMD的性能，当模态数量K设置过大时，相邻模态分量的中心频率则会相距较近，导致分解结果出现混频现象；当模态数量K设置过小时，有些模态包含在其他模态中或者原始信号中的一些重要信息将会被滤掉丢失。故本文引入最小巴士距离法[11]来确定模态数量K值，避免主观选择参数存在的偶然性和随机性。然而一直难以有效解决如何选择有效分量的问题。

为解决VMD算法存在的选择有效分量的问题，VMD复合算法成为研究热点。文献[12]提出VMD算法与相关系数联合的去噪方法(VMD-CC算法)在管道泄漏检测中的应用，利用相关系数法选择包含泄漏信息最丰富的BLIMF分量，克服了VMD算法分解后选择有效分量的盲目性，提高了管道泄漏检测的精度。文献[13]提出了VMD算法与能量值结合的信号去噪方法(VMD-EV算法)，计算各BLIMF分量概率密度函数的能量值，通过评估两个相邻能量值之间的变化，选择有效分量进行重构，此方法能够有效地应用于天然气管道小泄漏信号的去噪处理。

基于以上研究，为更好地解决VMD算法分解信号后如何选择有效分量的问题，解决信号中的噪声干扰问题，笔者提出一种VMD-ISD选择有效分量的算法，并与上文提到的VMD-CC算法、VMD-EV算法、WT算法进行对比，以输出信噪比、均方误差和平均绝对误差作为性能指标，试验结果表明,VMD-ISD算法得到了较好的去噪效果，验证了仿真信号去噪方面的优越性和应用在天然气管道泄漏信号去噪方面的可行性。

1 相关理论

1.1 VMD算法原理

VMD是综合维纳滤波、希尔伯特变换(Hilbert Transforms)、频率混合等理论的基础上提出的一种自适应的信号分解方法，可分为变分模型的构造和求解两个步骤。

VMD将一个输入信号分解为若干个相互独立的模态uk，相互独立的模态具有特定的稀疏特性，且每个模态都在围绕着其中心频率wk，为了获取每个模态的频率带宽，可采取以下方案。

对每一个模态uk进行Hilbert变换求解相应的解析信号，可以获取相应的单边频率:

(1)

利用指数因子e-jwkt对其修正,使得每个模态调制到相应的基频带上:

(2)

通过高斯平滑对信号进行解调，得到各个模态的带宽:

(3)

进而求解带约束条件的变分问题，其约束变分模型为:

(4)

其中uk={u1,u2,u3,…,uK}为各模态函数;wk={w1,w2,w3,…,wK}为各模态函数的中心频率。

为求解上述变分模型，利用二次惩罚项和拉格朗日乘子法的优势，引入了增广Lagrange乘子，如式(5)所示。

(5)

式中,α为罚参数；λ为Lagrange乘子。

利用交替方向乘子算法寻找最优解，步骤如下。

(1)对{uk},{wk},λ1,n初始化为0。

(2)当w≥0时，更新泛函数uk:

(6)

更新泛函数wk：

(7)

(3)当w≥0时，对其进行双重提升:

(8)

其中，γ为噪声容限，当去噪时，可以使γ=0得到更好的去噪效果。

(4)给定收敛阈值ε>0，重复(2)和(3),直到满足约束条件。

(9)

从整体上看，VMD算法以设定的迭代方式不断更新每个模态分量的带宽和中心频率，当满足式(9)时，停止迭代。最终，根据实际信号的频域特征得到预设的模态数量K值，完成了信号的自适应分割，以避免模态混叠问题。

1.2 板仓-斋藤距离

板仓-斋藤距离(Itakura-Saito Distance,ISD)是Bregman散度系列中一种常见的相似性度量方法[14]。ISD常用于语音识别，比较语音信号数据之间的相似性，作为衡量增强处理后语音的畸变程度的客观评价指标。ISD越小，衡量增强处理后的语音越逼近原始输入信号，即信号数据之间的相似度越高[15]。本文将ISD用于选择有效分量，评估各BLIMF分量与输入信号的概率密度函数(Probability Density Function,pdf)之间的相似性，选取有效分量，进行信号重构。

ISD公式定义如下：

(10)

式中，p，q为信号的pdf，都是由向量表示；n为p，q由向量表示的维数；D(p,q)表示p和q之间ISD的大小。

1.3 VMD-ISD算法原理

输入信号g(t)经过VMD分解得到K个BLIMFs，计算输入信号g(t)与各BLIMF分量的概率密度函数，记为pdf(g(t))和pdf(BLIMFi(t))，然后计算概率密度函数之间的ISD，通过ISD来表示输入信号g(t)和各BLIMF分量的相似程度L(i)，定义如下：

L(i)=ISD[pdf(g(t)),pdf(BLIMFi(t))]

(11)

通过评估两个相邻ISD之间的增量，以ISD增量最大的两个相邻BLIMF分量作为有效分量选择的转折点，识别有效分量，进行信号重构。当相邻的ISD之间增量最大时，表明在该BLIMF之后的相似性急剧下降，即ISD突变最大及其之后的BLIMF主要包含噪声成分，有效成分较少。θi为两个相邻ISD之间的增量，定义如下：

θi=L(i+1)-L(i) (i=1,2,…，N+1)

(12)

假设ISD增量差值最大在BLIMFm与BLIMFm+1之间，则第m个BLIMF分量作为有效分量和噪声分量的转折点，将前m个BLIMF分量作为有效分量，然后对噪声主导的噪声分量重构进行小波降噪处理，本文选取sym小波基进行3层分解，对分解后的小波系数进行阈值处理，再将处理后的小波系数进行重构，滤除噪声分量中的高频噪声，最后将有效分量与滤波后的噪声分量进行重构得到滤波信号，得到的滤波信号如下：

(13)

VMD-ISD算法简要流程如图1所示。

2 仿真信号验证

为验证本文提出的VMD-ISD算法鉴别有效分量的准确性，选取各分量为2,24,45 Hz三个频段的余弦信号作为原始信号并加入噪声强度为0.1的高斯白噪声进行仿真分析，即:

g(t)=cos(4πt)+0.5cos(48πt)

+0.25cos(90πt)+n

(14)

式中，n为噪声强度0.1的加性高斯白噪声，信号采样频率为1 000 Hz。

由图2，3可以看出，加入高斯白噪声后的复合信号中冲击成分被减弱，信号变得杂乱无章，不利于信号后续的提取特征。

为确定VMD算法的分解尺度K值，计算不同分解尺度K时VMD分解后各BLIMF分量之间的巴士距离，提取最小巴士距离(BDmin)。分解尺度K分别取2,3,4,5,6时，提取的BDmin分别为0.117 5,0.106 3,0.644 6,0.000 8,0.000 1。根据最小巴士距离法选取K=4，VMD分解后各BLIMF分量如图4所示。可以看出，复合信号中有效成分主要集中在前3个BLIMF分量，最后的BLIMF分量噪声成分居多。

根据式(11)计算各BLIMF分量与复合信号的pdf之间的ISD，如图5所示；ISD值大小如表1所示(表中加粗字体表示概率密度函数的ISD值增量最大，变化最显著)。由图5和表1可以看出，复合信号经VMD算法分解后从低频到高频BLIMF分量的ISD值整体呈上升趋势，且在BLIMF3-BLIMF4概率密度函数的ISD增量最大，变化最显著，因此BLIMF3作为有效分量和噪声分量的转折点，根据VMD-ISD算法选取BLIMF1,BLIMF2,BLIMF3作为有效分量，BLIMF4作为噪声分量，对噪声分量进行小波去噪，根据式(13)将去噪后的噪声分量与有效分量重构得到滤波信号。原始信号与滤波信号时域图如图6所示，VMD-ISD算法的重构误差如图7所示。

表1 概率密度函数的ISD

由图6可以看出，VMD-ISD算法的滤波信号几乎完美地复现原始信号，有效地去除信号中的噪声，突出了冲击成分，得到满意的滤波效果。

VMD分解得到的各BLIMF分量的中心频率如图8所示，其中，X表示为各BLIMF分量的中心频率，Y表示迭代次数。由图8可以看出，VMD算法分解信号具有很强的中心频率捕捉能力，且前3个BLIMF分量的中心频率正是复合信号中3个余弦信号的中心频率，因此复合信号有效成分主要集中在前3个BLIMF分量，最后的BLIMF分量噪声成分居多，与本文提出VMD-ISD算法对复合信号选取前3个BLIMF分量相符，验证了VMD-ISD算法鉴别有效分量的准确性。

为更加可靠地评估VMD-ISD的滤波效果，本文采用信噪比(SNR)、均方误差(MSE)、平均绝对误差(MAE)作为评价指标，计算公式定义如下：

(15)

(16)

(17)

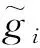
通常情况下，MSE，MAE相对越小，SNR相对越大，则证明算法的滤波效果越好。

对于复合信号，计算VMD-ISD算法、VMD-CC算法、VMD-EV算法、WT算法的滤波信号的SNR,MSE,MAE，并进行对比，试验对比结果见表2。 可以看出，VMD-CC算法、VMD-EV算法、WT算法对信号去噪后的SNR分别为12.065 2,19.661 3,16.540 5 dB,而笔者提出的VMD-ISD算法提高了信号的SNR，达到了20.426 1 dB。VMD-CC算法、VMD-EV算法、WT算法对信号去噪后的MSE和MAE与笔者提出的VMD-ISD算法相比，VMD-ISD算法的MSE和MAE最小，分别为0.077 6,0.062 3。

表2 去噪性能指标对比(复合信号)

结合以上对比结果，VMD-ISD算法得到了较为理想的滤波效果。

为了验证VMD-ISD算法的鲁棒性，输入信噪比从5 dB、以5 dB的步长变化到20 dB，分别与其他3种算法进行对比，不同输入信噪比在各算法下的试验结果如表3所示。可以看出，VMD-ISD算法的重构信号SNR高于其他3种算法，MSE和MAE低于其他3种算法，说明VMD-ISD算法去噪效果较好，且提出的算法具有较好的鲁棒性。

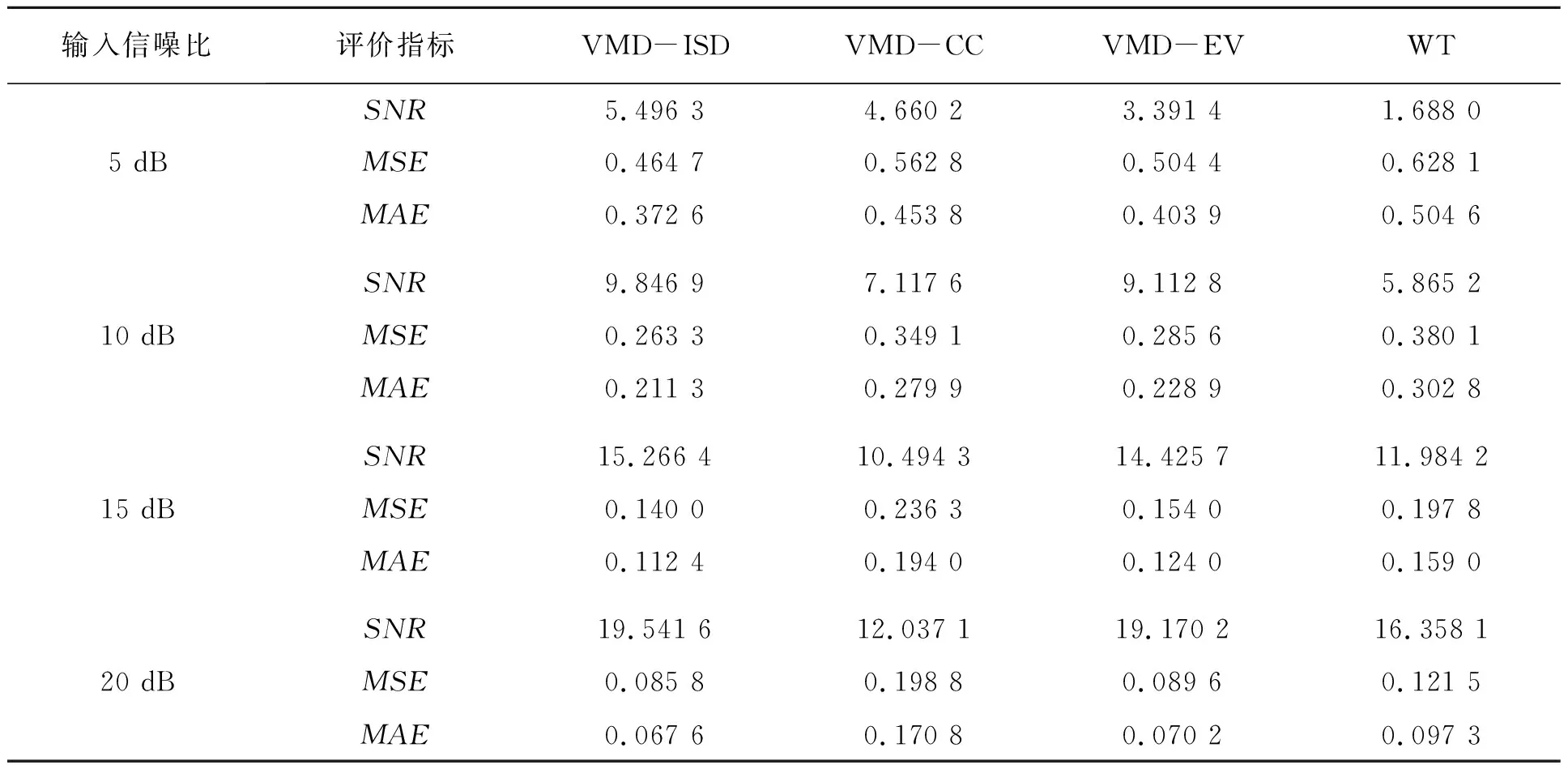
表3 不同输入信噪比在各算法下的试验结果

3 管道泄漏信号去噪分析

本文研究使用的管道总长183 m，管径为DN50。管道共设置了18个泄漏点，相邻泄漏点间隔10 m，每个泄漏点用4分球阀链接，用来模拟现场天然气管道的泄漏。试验利用 Labview 编程环境，采集卡型号为NI-9215采集板卡，采样频率3 kHz。利用安装的压电式声波传感器进行数据采集，并上传到计算机中进行数据处理。天然气管道泄漏信号是复合信号，包含较多的噪声，这将会对后续的管道泄漏检测造成干扰，因此利用本文提出的算法对天然气管道泄漏信号进行去噪，将会降低噪声对天然气管道泄漏检测的影响。实验室采集到的管道泄漏信号时域图和频谱图，如图9所示。

根据最小巴士距离法选取K=7。图10示出VMD分解得到的各个BLIMF分量。

计算泄漏信号与各BLIMF分量的概率密度函数之间的ISD，ISD趋势如图11所示，根据VMD-ISD算法选择BLIMF1-BLIMF5作为有效分量，对噪声主导的噪声分量BLIMF6,BLIMF7进行重构，并进行小波降噪，最后将有效分量与小波去噪的噪声分量进行重构，得到滤波信号。滤波信号时域图和频谱如图12所示。由图12可看出，重构信号保留了泄漏信号的基本特征，低频信号基本未受影响，高频信号明显被去除。

对于管道泄漏信号，计算VMD-ISD算法、VMD-CC算法、VMD-EV算法、WT算法的滤波信号的SNR,MSE,MAE，试验对比结果如表4所示。可以看出，VMD-CC算法、VMD-EV算法、WT算法对信号去噪后的SNR分别是16.258 6,19.727 3,18.150 2 dB,而笔者提出的VMD-ISD算法提高了信号的SNR，达到20.843 4dB。 VMD-CC算法、VMD-EV算法、WT算法对信号去噪后的MSE和MAE与笔者提出的VMD-ISD算法相比，VMD-ISD算法的MSE和MAE最小，分别为0.010 4,0.008 1。

表4 去噪性能指标对比(管道泄漏信号)

结合以上对比结果，VMD-ISD算法能够有效地应用于管道泄漏信号的去噪处理，并且得到了较为理想的滤波效果。

4 结语

在正确选取参数K值的基础上，针对VMD算法分解所得有效分量和噪声分量区分存在困难的问题，笔者提出了一种VMD-ISD选择有效分量的算法。通过仿真信号与泄漏信号进行试验，VMD-ISD算法能精确地选择有效分量，与VMD-CC算法、VMD-EV算法、WT算法相比，文中提出的算法对高斯白噪声有更明显的抑制作用，能够有效应用于天然气管道泄漏信号的去噪处理，为后续的特征提取、工况诊断奠定了基础。本文VMD-ISD算法的去噪能力在调幅-调频的仿真信号和实际的天然气管道泄漏信号得到了试验验证，但仍存在一些问题需要进一步研究和探索。

(1)文中是以天然气管道泄漏信号去噪为研究背景提出的VMD-ISD算法，是否适应于其他类型的泄漏并提高VMD-ISD算法泛化能力将是后续的工作。

(2)目前在试验中使用的数据为单泄漏源信号，利用文中所提算法对于多泄漏源的复合信号进行去噪需要进一步研究和探索。