城市轨道交通停车线布设方案综合评价方法

孟艳丽，胡 华，方 勇，刘志钢，汪 涛

（1.上海工程技术大学 城市轨道交通学院，上海 201620；2.上海交通大学 船舶海洋与建筑工程学院，上海 200240)

0 引言

城市轨道交通对于准点要求性较高，线路列车运行密度较大，列车在运营过程中难免发生故障。为降低故障事件影响，应在设计上保障列车在发生故障时，能够及时退出正线运营。因此，需要在线路沿线加设停车线，停车线布设的合理性对造价、故障救援和运营调度的灵活性都有直接影响。

国内学者针对城市轨道交通停车线已有一定研究。毛洁[1]针对停车线的运营需求和功能要求，描述了停车线的布置型式类别、特点及适用性；付意庄[2]综合考虑客流需求和运营管理需求，提出了有关停车线设计密度、位置、形式与长度的建议；徐立国[3]分析了不同停车线布置形式的优缺点后，提出停车线的最大布设间隔；翟倩[4]总结了设置不同数量渡线的停车线优缺点及在运营过程中影响；张增勇等[5]系统地分析了停车线在故障救援中作用和工程造价，并建立了0-1 规划模型，定量合理布设停车线数量与位置。

目前对城市轨道交通停车线的研究多集中在布置形式、布置位置方面，内容和因素较为单一，缺乏对停车线布设方案的综合性评价指标和评价方法的深入研究。因此，亟需综合考虑停车线布设的影响因素，定义量化评价指标，构建可定量的城市轨道交通停车线布设方案综合评价模型。

1 停车线布设影响因素分析

停车线具有供故障列车临时待避停放、备车停放、夜间工程车辆折返和临时调度折返等功能。停车线布设内容包括确定其布设位置、布设形式、设置条数和设计长度等，其主要影响因素如下。

（1）车站敷设方式和站台形式。为满足故障列车临时停放与每日首发的需求，停车线一般都设置在车站附近，因此车站敷设方式及其周围环境、水文地质管线等工程条件会影响停车线布设的位置、形式和长度等。当停车线布设于地下车站时，由于相比地面和高架车站其施工难度和建设成本较高，通常布设尽头式或三向贯通式、一列位长度的停车线，以减小停车线的规模和节约建设成本。据统计数据，对于地下二层车站增设1 条四向贯通式、二列位的停车线需增加投资0.6 亿～1.5 亿元。车站站台形式也会影响停车线的布设形式。一般情况下，高架车站选用侧式站台，地下车站选用岛式站台。对于侧式站台，由于线间距较小无法加设渡线，为便于相反方向故障列车的存放，可考虑加设渡线的单侧停车线；若考虑高架线与城市景观协调性，可在两侧对称布置停车线，侧式站台外侧式双停车线如图1 所示；对于岛式站台，可利用车站两端具有较大线间距的“喇叭口”设置内侧式停车线，岛式站台内侧式停车线如图2 所示。

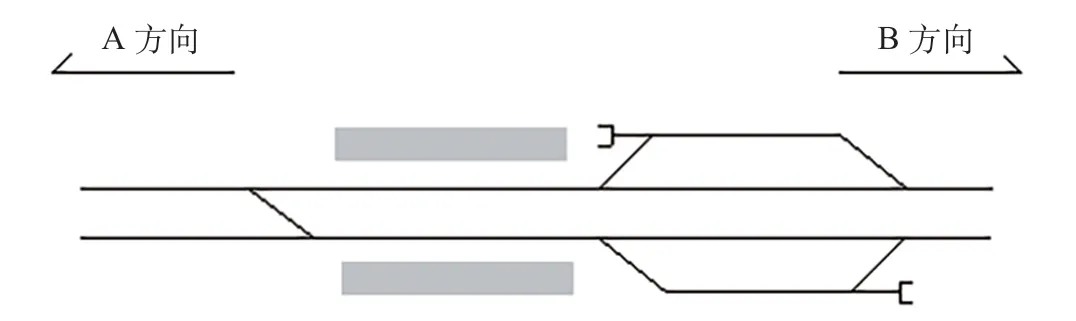
图1 侧式站台外侧式双停车线Fig.1 Outside double parking lines on a side platform

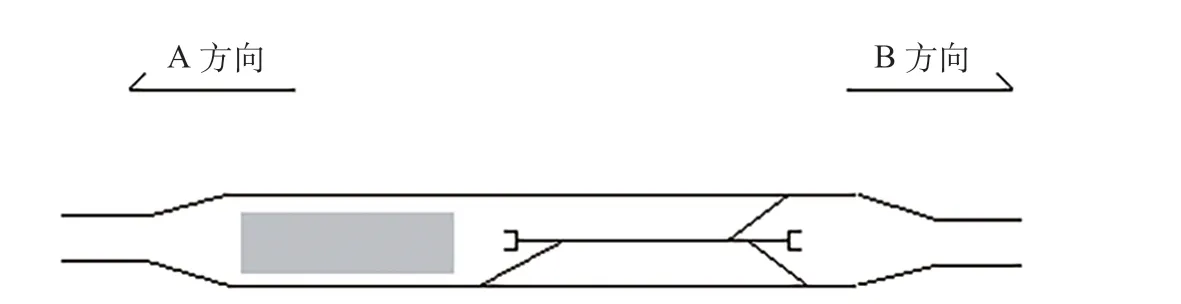
图2 岛式站台内侧式停车线Fig.2 Inside parking lines on an island platform

（2）车辆段与折返线的位置和形式。车辆段兼具故障列车的停放功能，双线折返线也具备临时停车功能，在确定线路停车线位置与布设密度时，应当将车辆段和具有停车功能的折返线的位置与数量作为停车线来考虑，以避免相同功能配线的重复设置，使得线路配线更加合理，在保障运营功能的前提下降低建设成本。如线路尽头的折返站未连接车辆段时，则需要结合折返线的设置布设停车线或存车线，可不必再考虑单独设置停车线。

（3）故障列车退出正线运营的时间要求。停车线的布设应当保证列车在运行出现故障时，能在规定的时间内完成故障处置，恢复线路正常运营。设有停车线的车站间距越小、布设密度越高、停车线的设计长度越长，建设工程投资就越大，相应地列车故障对正线运营的影响时间就会相应减短。根据上海地铁实际测算，一列位停车线在后续列车连挂故障车，将其推入停车线后仍需占用正线，须等待列车解钩，救援列车退回到正线，并且重新建立载客模式后，才能恢复该线路正常运营，相比二列位停车线预估增加故障影响时间8 min。《地铁设计规范》中有关停车线设置间距的规定，其控制目标是故障列车前方停车线的走行时间不大于20 min，故障车的处理下线时间不大于30 min。

（4）运营灵活性。运营灵活性涉及故障列车下线方式的选择便捷性、线路区间故障组织临时交路的可行性以及突发不均匀客流组织大小交路方案的多样性，与停车线及其辅助性渡线的布设形式关系密切。尽头式停车线，存放列车仅能从一个方向进出，反方向列车不便进入停车线且不能采取牵引式故障列车处理模式，灵活性较差，而贯通式停车线则能够使得线路故障列车快速处理下线，增加临时运营组织的灵活性。

2 评价指标体系构建

停车线布设影响因素具有多重性，其评价体系也具有多目标性，构建评价指标体系需要进行综合评价，得到城市轨道交通停车线布设评价指标体系如图3 所示，包括目标层P、准则层B与指标层C共3 个部分。其中准则层B包括工程条件B1、工程经济B2、故障救援B3、运营灵活B4；指标层C包含基坑安全性C11、交通运行状态C12共7 项。

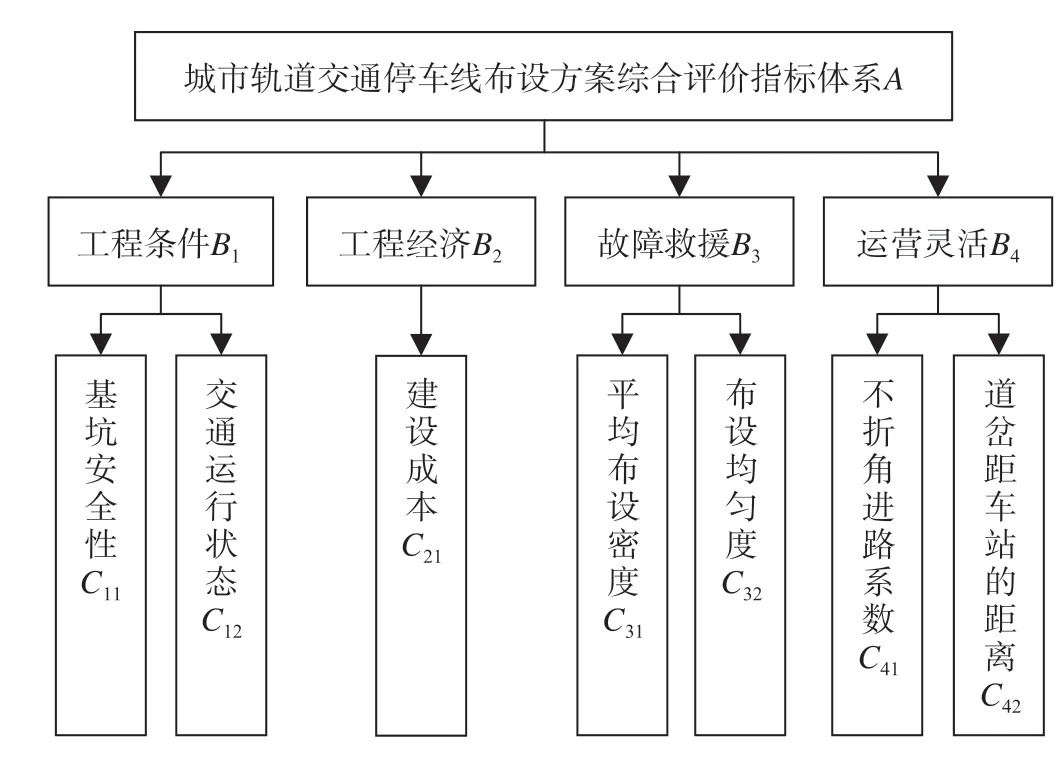
图3 城市轨道交通停车线布设方案综合评价指标体系Fig.3 Comprehensive evaluation index system of layout scheme for parking lines of urban rail transit

2.1 工程条件

停车线工程条件主要包括工程地质条件、周边建筑物情况以及地面交通分布情况等，是对停车线建筑有影响的各种因素的总称，可以用基坑安全性、交通运行状态2 个指标来进行衡量。

（1）基坑安全性。基坑安全性可描述停车线建设时期的施工难度，安全性越低表示需要的安全措施越多，施工条件越复杂，可通过风险指数R划分等级进行评价。其等级划分一般受3 个因素的影响：基坑开挖深度及支护性质；基坑周边建筑物、构筑物及环境对基坑开挖限制；水文地质和工程地质环境。结合上海地铁实际工程经验与已有研究成果[6-7]，基坑安全性等级划分标准如表1 所示。

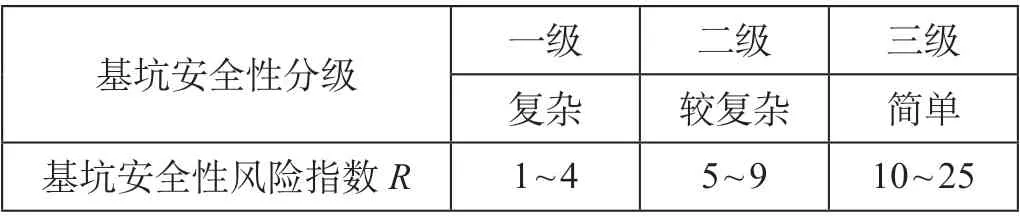
表1 基坑安全性等级划分标准Tab.1 Standard for safety grade classification of foundation pits

（2）交通运行状态。交通运行状态是用来描述车站停车线施工时对附近道路交通所造成的临时性影响程度的大小。停车线施工时对周围道路的干扰程度大小与停车线设置形式复杂性及数量成正相关。结合上海地铁实际工程经验与已有研究成果[8]，提出基于交通运行状态综合评价指数的等级划分标准如表2 所示。

表2 基于交通运行状态综合评价指数的等级划分标准Tab.2 Grade classification standard based on comprehensiveevaluation indexes of traffic running state

2.2 工程经济

停车线平均建设成本是指全线具有停车线功能的车站配线的平均建设成本。每处停车线的建设成本与停车线的工程量与单位公里造价有关，而单位公里造价与车站敷设方式密切相关，一般地下车站单位公里造价与地面和高架车站存在显著差异，需要分别考虑。停车线平均建设成本计算公式为

式中：F是指停车线平均建设成本，亿元/个；f1为高架与地面车站停车线的平均造价，亿元/km；l1为全线高架与地面车站布设停车线的总长度，km；f2为地下车站布设停车线的平均造价，亿元/km；l2为全线地下车站布设停车线的总长度，km；m为全线布设停车线所需的道岔个数，个；t为道岔的平均单价，亿元；n1为全线布设停车线的车站数，个。

2.3 故障救援

（1）平均布设密度。平均布设密度指全线具备停车线功能(如停车线、出入库线和布设停车线的折返线等)的车站数与全线总车站个数的比值，即平均每间隔多少个车站布设1 条停车线，计算公式为

式中：ρ为全线停车线平均布设密度；N为全线车站数，个。

（2）布设均匀度。布设均匀度指具备停车线功能的车站在全线空间上的分布均匀程度，用具有停车线功能的车站的最大相邻站间距与平均相邻站间距的比值来表示，计算公式为

式中：γ为停车线布设均匀度；lmax为全线具有停车线功能的相邻车站的最大站间距，km；l-为全线具有停车功能的相邻车站的平均车站间距，km。

2.4 运营灵活性

（1）不折角进路系数。上行或下行的正线与逆向道岔构成的进入停车线的进路是不折角进路，不折角进路系数是指全线上下行方向连接停车线和正线之间的逆向道岔数量与顺向道岔数量的比例。其计算公式为

式中：η为停车线不折角进路系数；r1为全线连接停车线和正线之间的逆向道岔数量，个；r2为全线连接停车线和正线之间的顺向道岔数量，个。

当停车线布设成尽头式或四向贯通式时，其布设的顺向道岔和逆向道岔的数量相同，此时停车线不折角进路系数η为1，四向贯通式停车线如图4 所示。当停车线布设成三向贯通式等非对称形式时，其停车线不折角进路系数η为2，三向贯通式停车线如图5 所示。

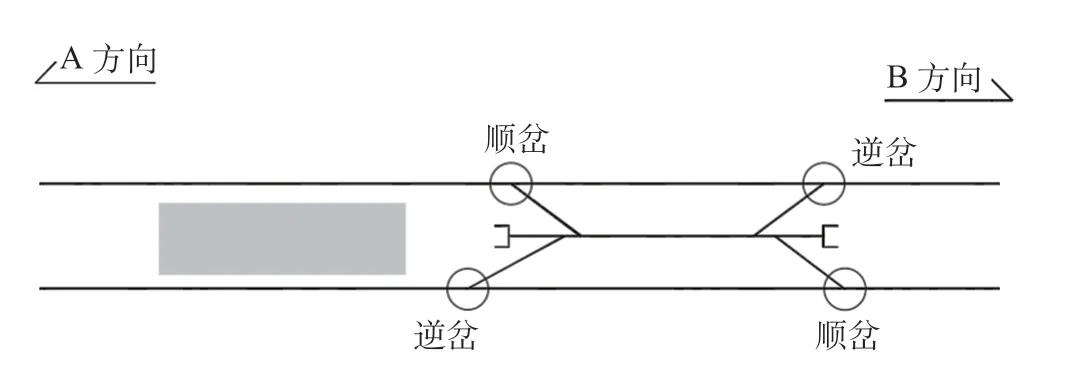
图4 四向贯通式停车线Fig.4 Four-way through parking lines

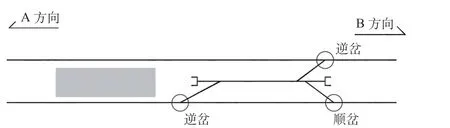
图5 三向贯通式停车线Fig.5 Three-way through parking lines

（2）道岔距车站的距离。道岔距车站的距离是指全线具有停车线功能的车站站台端部与该站停车线最远处道岔中心的距离均值，它主要与停车线的布设形式(横列式或纵列式)有关。在道岔自动控制失效情况下，需执行人工扳道岔等应急处置措施，道岔与车站距离相距较远将给车站运营管理及故障处置带来不便。道岔与车站的距离计算公式为

式中：d-为全线停车线最远端道岔与所在车站端部的平均距离，m；di为第i个车站的停车线最远端道岔与车站端部的距离，m。

3 综合评价模型的构建

AHP-TOPSIS-雷达图综合评价模型是将层次分析法[9]、 优劣解距法与雷达图分析法三者有机结合，AHP 先将多目标决策问题展开分解为多层次的准则和指标，定量指标与模糊量化定性指标求出各评价方案的综合权重值，再分别使用TOPSIS 法和雷达图分析将各方案的优劣进行排序，使评估结果在最大程度上合理地反映专家的主观意向，选择建立结合AHP，TOPSIS 与雷达图分析作为停车线布设方案综合评价模型。

3.1 构造判断矩阵

采用专家打分构造目标层与准则层判断矩阵，指标相对重要性比较可利用1-9 标度计算，1-9 标度意义如表3 所示。记矩阵中元素aij为指标i与指标j的比值，其中aij＞0，且aji=1/aij，通过各级指标层判断因子之间的两两比较得到判断矩阵A，计算公式为

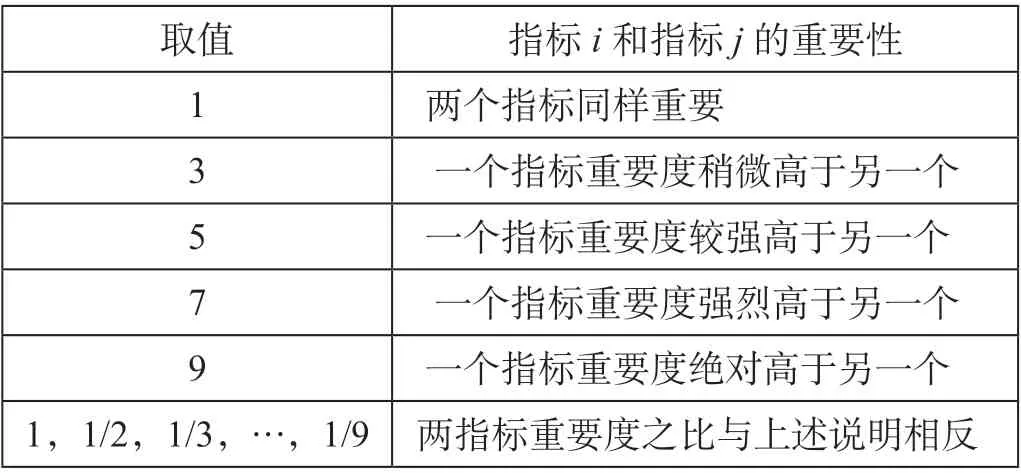
表3 1-9 标度意义表Tab.3 Meaning of scales1-9

3.2 一致性检验

根据各平均一致性指标，矩阵阶数n与最大特征值λmax，算出A的一致性指标指数CI，计算公式为

随机一致性指标RI值如表4 所示。

表4 随机一致性指标RI 值Tab4 RI value of the random consistency index

在表4 查找对应的平均随机一致性指标，最后计算一致性比率CR，计算公式为

如果判断矩阵A的最大特征值为λmax=n，则一致性指数CI= 0，判断矩阵A为一致性矩阵，一致性指数越大，矩阵的不一致性越大。若CR＜ 0.1，则认为A具有满意的一致性；若CR＞ 0.1，需要专家打分重新建立判断矩阵。

3.3 指标权重的计算

采用算术平均法求权重，计算步骤如下。

（1）判断矩阵A为n阶方阵，将其按列归一化，得到新的矩阵A1，其计算公式为

（2）将归一化的各列相加，即按行求和；

（3）该判断矩阵的权重向量等于将相加后得到的向量中每个元素再除以矩阵行数n。算术平均法求得的权重向量计算公式为

（4）按照以上方法分别计算出评价指标体系中准则层与指标层的相对权重，最后得到总权重。

3.4 数据指标标准化

将不同指标进行正向化处理，统一转化为效益型指标，即数值越大越好的指标。然后将正向化得到的效益型指标作标准化处理，以此消除不同指标的量纲影响。m个评价方案、n个评价指标(指标均已正向化)所构成的正向化矩阵X表示为

对以上标准化的矩阵记为Z，Z中的每一个元素zτφ计算公式为

3.5 计算正负理想解与贴近度

（1）定义正理想解最大值Z+，其计算公式为

式中：L为由评估方案贴近度值构成的评估矩阵；W为采用AHP 计算所得的综合权重向量。

3.6 雷达图分析

对评价指标利用公式(12)消除不同量纲之间的影响后，可按以下步骤进行雷达图分析。

（1）评价指标权重值与雷达图角度的转化由指标个数m绘制雷达指标轴，利用公式(10)得到指标权重，其指标轴间旋转角计算公式为

式中：αj为指标轴间夹角，单位度；ωj为指标权重。

（2）雷达图的绘制，利用CAD软件，对标准化后的评价指标的数值投影在对应的指标轴上，并将每个值的投影点连接成线，形成最终的雷达图。

（3）确定评价系数，以雷达图的平均面积及周长作为评价函数的特征量，雷达图的平均面积∂1、周长∂2分别为

4 实例分析

4.1 数据搜集

选取上海地铁1 号线与9 号线的停车线布设方案作为研究实例，进行数据调查分析，上海地铁1号线停车线布设图如图6 所示，其设有梅陇、富锦2 个车场以及其他5 个具有停车线功能的车站；上海地铁9 号线停车线布设图如图7 所示，其设有九亭、金桥2 个车场及其他7 个具有停车线功能的车站。

图6 上海地铁1 号线停车线布设图Fig.6 Parking line layout of Shanghai Metro Line 1

图7 上海地铁9 号线停车线布设图Fig.7 Parking line layout of Shanghai Metro Line 9

根据图3，统计上海轨道交通1 号线与9 号线停车线评价指标原始数据，得到上海地铁1 号线与9 号线停车线评价指标数据如表5 所示。

表5 上海地铁1 号线与9 号线停车线评价指标数据Tab.5 Evaluation indexes for parking lines of Shanghai Metro Lines 1 and 9

4.2 方案评价

（1）确定权重。根据图3 城市轨道交通停车线布设方案综合评价指标，基于专家打分得出各个判断矩阵。准则层对应的判断矩阵A为

一致性指标CI为0.046，一致性比例CR为0.052，由于CR＜0.10，判断矩阵A满足一致性要求。根据算数平均法公式(10)求得准则层权重值为：ω1= 0.092，ω2= 0.117，ω3= 0.487，ω4= 0.304，其排序为：故障救援＞运营灵活＞工程经济＞工程建设。

同理得到指标层C各指标的权重值，得到指标层C各指标在其所在准则层权重和目标层总权重。汇总指标层在其所在准则层和目标层权重与排序，得到权重排序表如表6 所示。由表6 可以看出停车线布设合理性权重排序前三的评价指标为：布设均匀度C32，不折角进路数C41和停车线平均建设成本C21。

（2）正理想解Z+、负理想解Z-与贴近度的计算。根据公式(10)将表4数据经过正向化和标准化处理后，再根据公式(16)、公式(17)计算标准化矩阵Z中每个指标的正理想解与负理想解，得到评价指标对应评价方案正负理想解表如表7 所示。

表7 评价指标对应评价方案正负理想解表Tab.7 Positive/negative ideal solutions in evaluation schemes corresponding to evaluation indexes

由表6 与公式(16)、公式(17)、公式(18)计算出1 号线与9 号线在工程条件、工程经济、故障救援与运营灵活4个方面对应正理想解的贴近度，评价方案相对贴近度如表8 所示。

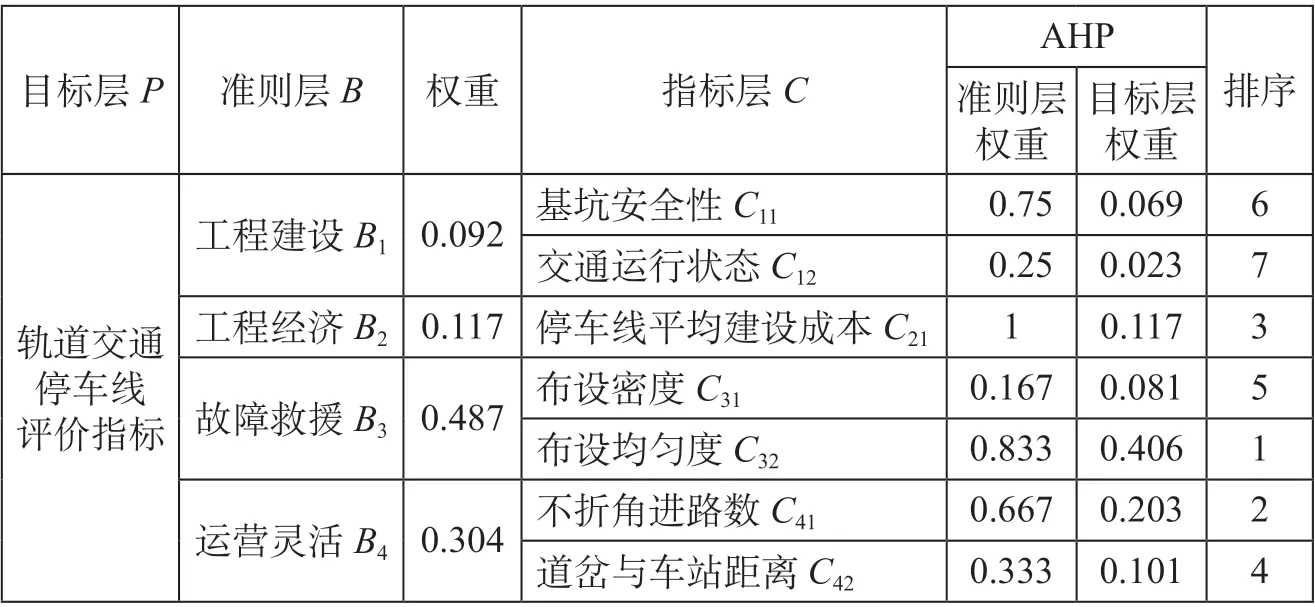
表6 权重排序表Tab.6 Sort table of index weights

根据公式(19)得到1 号线与9 号线的综合方案优越度分别为0.422，0.578，综合评价结果为9号线的停车线布设方案优于1 号线。从初始数据来看，1 号线与9 号线停车线设计指标数据无法辨别优劣，但数据经过正向标准化统一量纲后，利用TOPSIS 结合层次分析方法，最终得出具有多属性指标的轨道交通停车线设计的最终得分，显然9 号线得分高于1 号线。从表8 可知，在工程经济与运营灵活方面1 号线优于9 号线，但工程条件与故障救援9 号线皆为最优。因此，对应9 号线停车线布设改造应注重降低停车线的建设成本与提高运营灵活性，而对于1 号线则更应重视工程条件与故障救援方面的布设目标优化。

表8 评价方案相对贴近度Tab.8 Relative closeness of evaluation schemes

（3）绘制雷达图。根据公式(12)、公式(20)确定指标轴与指标夹角，绘制1 号线与9 号线综合评价指标雷达图如图8 所示。

从图8 可以看出各个评价指标的相对优劣程度。例如9 号线，其中2 个指标等于理想值，4 个指标比平均水平高，1 个指标较低。

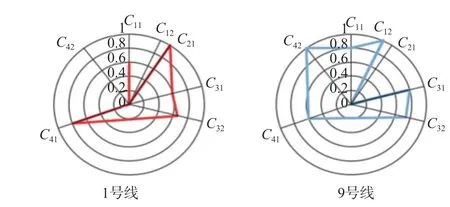
图8 1 号线与9 号线综合评价指标雷达图Fig.8 Radar chart of comprehensive evaluation indexes for Lines 1 and 9

（4）计算雷达图的评价系数。根据公式(20)—公式(24)得出1 号线与9 号线雷达图系数如表9 所示。

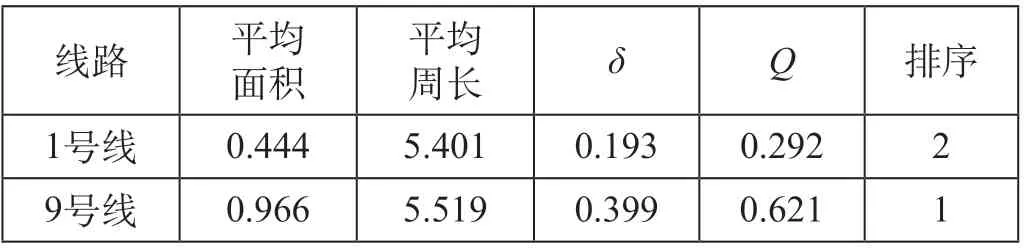
表9 1 号线与9 号线的雷达图系数Tab.9 Radar chart coefficient of Lines 1 and 9

根据雷达图分析的结果排序为9 号线优于1 号线，与采用TOPSIS 分析后的评估方案排序结果统一，证明了构建的评价指标与评价模型的合理性和有效性。

5 结论

（1）综合考虑停车线布设的工程和运营需求，分析了停车线的位置、条数、形式和长度等设计要素的影响因素，从工程条件、工程经济、故障救援和运营灵活性4 个方面提出了7 个评价指标的定义及量化方法。

（2）构建了综合AHP，TOPSIS 以及雷达图分析的停车线布设方案评价模型，先运用AHP 将多目标决策问题细化分解为若干层次的准则及指标，求出各评价指标的综合权重值，再分别使用TOPSIS 法和雷达图分析结合综合权重值将评估方案的标准化得分值进行排序，使评估结果在最大程度上合理地反映专家的主观建议。

（3）通过对上海地铁的实例评价，验证评估方法在停车线布设中的合理性与有效性。研究成果能够为我国城市轨道交通线路停车线的新建、改建等工程方案提供评价指标和方法依据。

（4）在未来研究中，可针对不同城市的轨道交通线路敷设特征及停车线布设情况，分类完善评价指标体系，并可引入离差最大化、熵权法等客观赋权法确定指标权重，进一步克服计算结果受主观因素的影响。