考虑运力恢复的铁路突发事件救援资源调配模型研究

张 涛，王振东，刘文浩

（1.中国铁道科学研究院集团有限公司 通信信号研究所，北京 100081；2.中国铁道科学研究院集团有限公司 国家铁路智能运输系统工程技术研究中心，北京 100081)

0 引言

铁路突发事件具有广泛性、频发性、多样性等特征[1]。突发事件导致运力骤降，形成运力瓶颈，进而引发列车运行偏离图定计划，其表现形式为列车晚点。救援指挥人员是突发事件救援处置工作的宏观协调者和组织者，担负着规避次生灾害、恢复运输秩序并按图行车的重要责任。随着铁路信息化水平和行车指挥自动化程度的不断提高，救援方案决策及指令发布呈现高度集中化的发展态势，救援指挥人员凭借自身经验合理调配救援资源并快速恢复运输秩序的难度不断增大。

国内外学者针对晚点总时长和晚点列车数这2类量化指标，对突发事件下的运输秩序恢复策略进行了研究。柏赟等[2]设计了列车晚点恢复的启发式算法。Goverde[3]通过提升运行图鲁棒性，有效降低单次列车晚点的传播力。周晓昭等[4]将车底接续关系纳入调整模型，并以改进和声算法求得晚点总时长和晚点列车数的双重较优。以上学者的关注焦点在于晚点已为既成事实，如何快速恢复运输秩序。

晚点不是突变产生的，是非正常停车或运缓等列车运行状态在时间维度上积累的结果[5]。从准点运行到晚点出现且呈增长态势的初期发展阶段，是救援指挥人员采取措施、发布指令最为密集的阶段。一些学者针对此阶段进行了大量研究。Corman 等[6]构建了基于感知控制和增强学习智能算法的行车冲突动态预测模型，为预先消解关键冲突提供了决策支持。邓念等[7]设计了列车运行计划实时调整模型，能够在干扰初期及时介入并给出列车运行计划调整策略。曾壹等[8]设计了实时抗干扰的晚点恢复模型，从微观层面组织列车避让干扰区段，控制晚点扩散。以上研究成果能够有效抑制列车早期晚点的传播与发展，但未将消解运力瓶颈纳入决策过程，在实际运用层面具有一定局限性。

事实上，突发事件导致的运力瓶颈存续时长是决定列车晚点总量的权重因素。在无应对措施干预的情况下，列车晚点总量与运力瓶颈的存续时间呈正相关，且随着抵近运力瓶颈区域的列车逐渐增多，晚点总量随时间增益的幅度会大大升高。因此，救援指挥人员在运力瓶颈存续期内的工作重点是在保证列车运行安全的前提下，组织救援力量尽快消解运力瓶颈，为后续的运输秩序恢复奠定基础。结合救援指挥人员处置突发事件的实际决策过程，构建考虑运力恢复的救援资源调配模型，以快速消解运力瓶颈及在此基础上的综合效果最优为目标，采用有限域穷举算法和优劣解距离算法(TOPSIS)求得最优解，并进行算例验证。

1 问题描述与分析

1.1 救援事件

运力瓶颈是由救援指挥人员依据获取到的突发事件信息而人为设定的。救援指挥人员第一时间获取到的突发事件信息较为宏观，如车体剧烈摇晃、接触网挂有异物、风雨雪等恶劣环境、旅客突发状况、区间异常红光带、信联闭故障等，往往对应多种诱发因素，并可能引发次生灾害[9-10]。诱发因素及次生灾害统称为潜在故障。基于“故障导向安全”原则，在潜在故障排除前，救援指挥人员须最大化设定运力瓶颈的影响深度及广度。潜在故障需要专业人员、救援机具等救援资源进行施救或排查，救援资源分布于各专业工区、综合维修工区、动车运用所等处，列车上也具备随车机械师、乘务组等处置力量。研究将资源分布处所统称为出救点。问题描述及分析如下。

对于某突发事件引发的运力资源瓶颈，存在潜在故障集合G，覆盖宏观突发信息所对应的所有潜在故障。当运力瓶颈可自行恢复，且不会引发次生灾害时，G= ∅，运用传统的晚点消解方法[2-4]进行运行图调整即可。对于需要人工或机具排除的潜在故障，集合G= {g1，g2，…，gi，…，gI}，包含I个潜在故障gi，∀i∈N*∩i≤I；同理，存在救援资源集合R= {r1，r2，…，rm，…，rM}，∀rm∈R，及出救点集合S= {s1，s2，…，sj，…，sJ}，∀sj∈S。参与救援潜在故障i的出救点集合表示为S i，S i⊆S。各类资源的量纲不同，考虑到同类救援人员常编排为班组，关键救援机具也是按照单位数量登记造册，令hjm表示第j处出救点所储备第m种救援资源的单位数量。令aim表示潜在故障gi对救援资源rm的需求量。令E(aim)为考虑救援力量整体工作效率及配合程度的资源期望需求量，是由历史统计数据中的极值及中位数加权求和得出，表示为

1.2 资源调配策略描述

式中：当行向量的模均不等于0 时，表示出救点j参与了救援。令矩阵X '= [X1，X2，…，Xj，…，XJ]T表示各出救点是否参与了故障救援。

1.3 剩余运力占用成本

出救点j的资源到达现场所占用的剩余运力资源量为ECRj，与出救点到施救地点的运输径路长度成正相关。为简化模型，令ECRj等于救援径路包含的闭塞分区数，救援径路所覆盖的线路所等同于1 个闭塞分区；车站以进站、进路和出站信号机为分割点，计算其等价的闭塞分区数。由于运力资源瓶颈前方区域的资源随着正常运行列车的逐渐远离而得到自然释放，占用前方区域运力资源进行故障救援不会加速剩余运力资源量的消耗。此外，部分出救点具备高效的路外机动能力，不占用铁路运力资源。假设同一出救点派出的不同救援资源由同一交通工具集中运送且一次完成，则出救点J参与救援所占用的剩余运力资源成本COSTj表示为

式中：二元变量δj∈ {0，1}，出救点在瓶颈前方时，δj= 0，否则δj= 1；二元变量βj∈ {0，1}，需要采用铁路运输方式到达现场时βj= 1，否则βj= 0。

各出救点参与救援占用的剩余运力成本为COST*= [COST1，COST2，…，COSTJ]，整体运力资源成本为COST=COST*×X '。

1.4 运力瓶颈消解时间

资源出救点到达现场的时间为tOD sj，是一个先验数据，通过日常巡检、维修、施工等工作记录统计得出。若潜在故障gi为基础设施故障或必须紧急制动并等待救援的列车故障，则潜在故障消解时间ti为

式中：E(aim)为资源期望需求量，表示潜在故障gi

若运力瓶颈发生在区间，某些场景下，按照《铁路技术管理规程》要求，列车经甩车处理或停车检查确认后，需运用自有动力以规定限制速度运行至相邻车站待避检修，于潜在故障区域救援完毕，且潜在故障列车出离故障区间后解除运输瓶颈。令FT表示故障列车出离故障区间的时间，min。潜在故障消解曲线如图1 所示。

图1 潜在故障消解曲线Fig.1 Potential fault resolution curve

2 救援资源调配模型

2.1 资源调配策略与潜在故障救援时间的调节关系

2.2 资源调配策略综合评价方法

步骤4：综合考虑社会影响、旅客满意度、作业风险等因素，对集中潜在故障进行权重分配，即ωj∈ (0，1]，∃j∈ {1，2，…，n+1}。

步骤5：分别计算各评分对象与最优解和最劣解的距离，构建综合评分公式，以得分作为评价优劣的依据，得分最高的资源调配策略是最优策略。

最优解为

得分最高的XTOPSIS为最优策略。

2.3 建立模型

为保证救援效果贴合预期，在潜在故障救援需求和资源分布的边界约束下，压缩运力瓶颈存续时间，并在此基础上比选综合最优策略，建立模型如下。

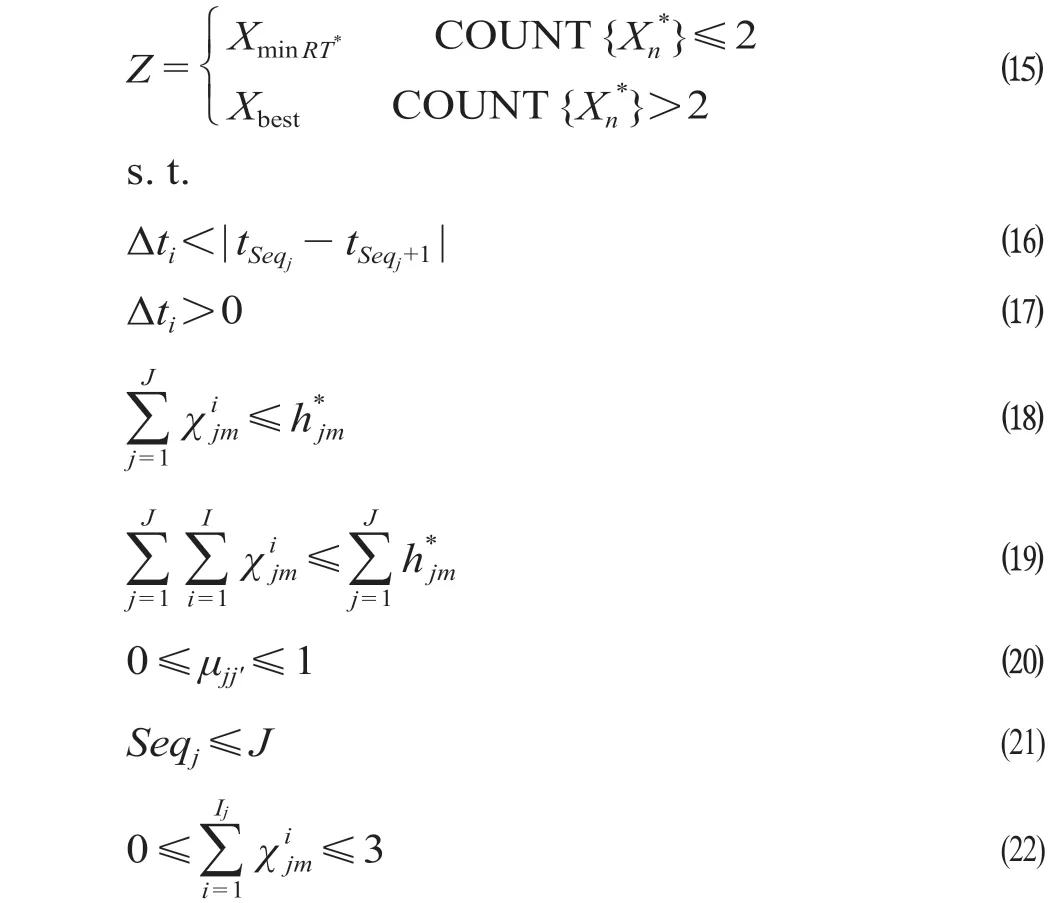
公式(16)为资源调配策略计划内的救援资源全部到位后的检修作业延续时间，应小于下一组救援资源的到达时间，否则就将下一组救援资源纳入救援计划；公式(17)表示调配策略计划内的最后一组救援资源到位后的工作时间应大于0，否则取消最后一组救援资源；公式(18)为从出救点j调用的救援资源m不能超过该出救点的等效资源储备量；公式(19)为调用m类救援资源量不能超过等效资源储备总量；公式(20)和公式(21)分别约定了合作效率增益系数及出救点数量的取值区间；公式(22)为考虑到出救点班组轮替机制及机具的常规配置数量，同一出救点最多派出3 个单位救援资源。

3 模型求解

由于潜在故障数量、出救点的数量及救援资源部署规模均有限，资源调配策略的数量是可控的。研究基于有限域穷举算法构建目标搜索方案，确保在较短时间内求得精确的全局最优解，基于穷举搜索算法和TOPSIS 算法的求解流程如图2 所示。

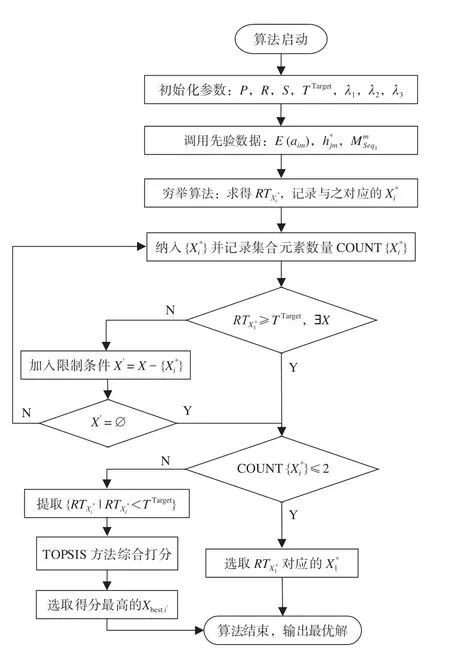
图2 基于穷举搜索算法和TOPSIS 算法的求解流程Fig.2 Solving process based on exhaustive search algorithm and TOPSIS algorithm

步骤4：运用TOPSIS 算法，比选出得分最高的XTOPSIS，并终止运算。

4 算例验证

某一运力瓶颈存在4 种潜在故障，共需6 种救援资源，且FT= 0。救援指挥人员对本次救援组织工作的乐观程度适中，即无明显的主观偏向，令λ1=λ2=λ3= 1/3。资源期望需求矩阵的先验数据赋值如表1 所示。

表1 资源期望需求矩阵的先验数据赋值Tab.1 Prior data assignment of resource demand matrix

各出救点等效资源储备量矩阵的先验数据赋值如表2 所示。

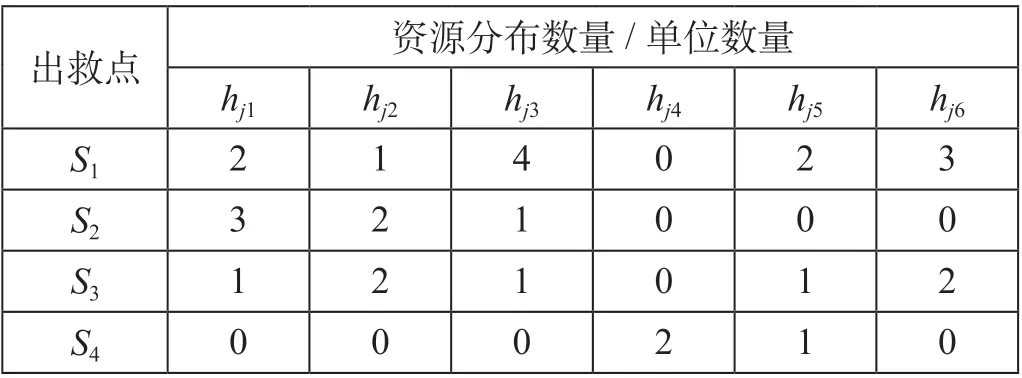
表2 各出救点等效资源储备量矩阵的先验数据赋值Tab.2 Prior data assignment of equivalent resource reserve matrix at each rescue point

由于g4是非资源敏感型潜在故障，即其救援时间不随救援策略的调整而变化，将其剔除综合打分范围。剩下的4 个方面权重依次为：0.2，0.1，0.2，0.5。运用TOPSIS 算法对其进行综合打分，得出以下结果。

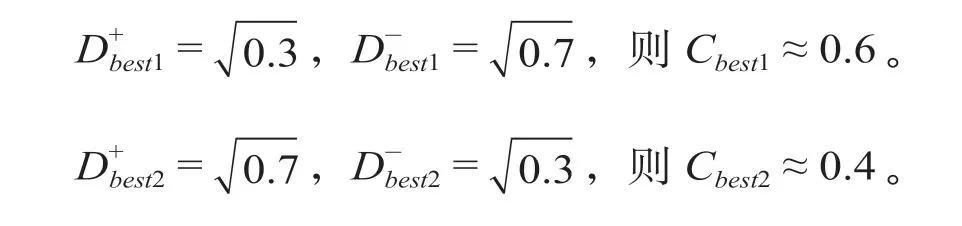
5 结束语

突发事件与运输秩序紊乱之间存在中间环节，即运力瓶颈。基于铁路应急救援机制构造约束条件，以救援指挥人员关注的运力恢复为求解目标，设计了运力瓶颈存续期间的救援组织模型，模型描述了多种救援资源、多出救点共同参与施救的协同机制。设计综合目标搜索算法求得最优解，输出结果符合救援预期。后续研究将把运力恢复与传统晚点消解进行整合，设计两阶段优化综合调整模型，进一步提升覆盖全过程的智能化处置水平。