考虑多类型时间窗的集装箱多式联运路径双目标优化研究

孙 岩，虞 楠，王丹竹，陈伟建

（1.山东财经大学 管理科学与工程学院，山东 济南 250014；2.交通运输部水运科学研究院 物流工程技术研究中心，北京 100088；3.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081；4.中车建设工程有限公司 城轨运营事业部，北京 100078)

0 引言

在经济全球化的驱动下，商品流通日益繁荣，运输需求日益旺盛，运输渠道显著延长，运输网络迅速扩张，运输环境更加复杂，从经济性、时效性等方面对运输业提出了挑战。在此背景下，依靠单一运输方式的运输组织形式已经无法满足客户的运输需求[1-2]。作为一种先进的运输组织形式，集装箱多式联运以标准化集装箱为载运单元，综合利用铁路、公路、水路等不同运输方式的优势，为客户提供灵活、高效、多样的运输服务，并在全球范围内得到了迅速的推广和应用[3]。随着集装箱多式联运网络的不断发展完善，作为提高集装箱多式联运系统运营效率关键的路径优化问题得到了学界和业界的广泛关注[4]。

目前，关于集装箱多式联运路径优化的文献较为丰富。张建勇等[5]在构建多式联运网络的基础上，构建了以总成本最小为优化目标的多式联运路径规划模型。在文献[5]的基础上，王涛等[6]研究了多式联运的运输方式组合优化问题，构建了优化模型，设计了基于Dijkstra 算法的启发式算法。张运河等[7]以总成本最小为优化目标研究了多式联运的最短路问题，通过在多式联运网络中增加虚拟发站与到站，使得问题求解可以借助Dijkstra 算法。魏航等[8]研究了时变网络下的多式联运最短路问题，在对多式联运网络进行变形处理的基础上构建了优化模型，并设计了基于Dijkstra 算法和动态规划的求解方法。Sun 等[9]以最小化运输成本以及降低碳排放为目标，研究了考虑时间随机性的多式联运路径双目标优化问题。蒋琦玮等[10]研究了运输时间不确定下的多式联运路径优化问题，构建了问题优化的机会约束模型，设计了问题求解的启发式算法。

近年来，随着准时生产等先进生产策略的应用，客户对运输时效性的重视程度越来越高。尤其是多式联运应用于长距离运输中，往往因运输组织方案规划不合理导致运输距离增加，造成多式联运经济性和时效性优势发挥不够显著的问题。既有研究也采取了多种方法以提高集装箱多式联运路径优化的时效性。陈雷等[11]在研究考虑碳排放的多式联运路径优化时规划了运输时限约束，使得集装箱到达终点的时间不超过给定的运输时限。Verma等[12]在规划危险品公铁联运路径时，以及Sun 等[13]在研究考虑开行方案的多商品流多式联运路径优化时均构建了运输时限约束。梅梦婷等[14]将运输时间最小化作为优化目标，构建了多式联运路径优化的“成本-时间-碳排放”多目标优化模型，设计了问题求解的带精英策略的非支配排序遗传算法。与文献[13]的时效性优化方法相同，Sun 和Xiong等[15-16]均构建了多式联运路径优化的“费用-时间”双目标优化模型，设计了求解问题帕累托解的算法。除规划运输时限约束、构建多目标优化2 种方法外，既有文献提出了采用时间窗刻画约束时间对多式联运时效性进行优化。Zhang 等[17]在规划考虑碳排放的多式联运路径优化时规划了时间窗约束，保证集装箱在规定的时间窗内运到终点。与文献[17]相反，Sun 等[18]认为集装箱可以较规定的时间窗提前或者延迟到达终点，但是会导致惩罚费用的产生，据此研究了带有时间窗的多式联运路径优化问题。

既有文献在多式联运路径优化研究上取得了一定的成果，但仍然存在不足之处。①多式联运网络中的一些中转节点存在固定作业时间窗限制了节点中转作业的进行[19]，而上述文献忽略了节点固定作业时间窗对中转作业的限制，影响多式联运路径优化的可行性。②在优化多式联运时效性时，规划运输时限约束往往会导致集装箱提早运到终点，致使仓储保管等额外费用的产生。同时，运输的准时性并不总是意味着运输时间越短越好。此外，采用时间窗刻画运输时限符合客户对集装箱运到终点的准时性需求，但是构建硬时间窗约束忽视了客户在一定程度上接受集装箱提前或延迟运到终点这一事实，而采用软时间窗构建惩罚费用时，单位惩罚费用取值往往难以准确确定，并且集装箱提前或延迟运到终点并不一定会在短期内产生经济损失[20]。

为此，对集装箱多式联运路径优化问题进行研究，并在优化建模时考虑2 类时间窗：①规划中转节点固定作业时间窗硬约束，保证集装箱到达此类节点时的时刻在其固定作业时间窗内，从而保证后续中转作业的进行；②规划运输时限软时间窗，据此规划集装箱运到终点的提早或延迟时间，并以其最小化构建多式联运时效性目标，提高多式联运路径规划的准时性。据此，构建考虑多类型时间窗的多式联运路径优化双目标混合整数线性规划模型，采用标准化加权求和法结合数学规划软件对问题进行求解，进一步分析多式联运路径优化的经济性目标和时效性目标的关系，为多式联运经营人根据客户需求规划运输方案提供定量支持。

1 集装箱多式联运路径双目标优化研究

1.1 问题描述

一批集装箱需要在客户规定的运输开始时刻从起点通过多式联运(综合考虑铁路运输、公路运输和水路运输3 种运输方式)运至终点。多式联运路径优化即选择一条最优的运输路径实现集装箱起点至终点之间的运输。在进行优化时，研究将平衡多式联运成本与效率之间的关系，考虑中转节点的作业时间窗约束，保证多式联运路径优化方案在时间和空间上的可行性。假设如下。

（1）集装箱在运输过程和中转过程中不可拆分，即集装箱最多采用1 种运输方式在节点间进行运输，并在中转节点上最多进行1 次不同运输方式间的中转。

（2）多式联运网络中运输方式的运输能力，以及中转节点的中转作业能力均满足该批集装箱的运量要求。

（3）集装箱的运输信息(包括起点、终点、运量及运输时限等)，以及多式联运网络的参数信息(包括网络结构、时间、费用等)均是已知的、确定的。

1.2 优化建模

1.2.1 符号及其表示

以G= (N，A，S)表示多式联运网络，其中，N表示多式联运网络中的节点集合，A表示多式联运网络中的有向弧集合，S表示多式联运网络中的运输方式集合。一批集装箱需要采用多式联运从起点(标号为o)运至终点(标号为d)，其运输量为q(单位为TEU)，运输开始时刻为t0，运输时限时间窗为[ηmin，ηmax]。

优化建模所需的其他符号如下。

（1）标号、集合、参数。h，i，j为多式联运网络中的节点标号，且有h，i，j∈N；(i，j)为多式联运网络中由节点i到节点j的有向弧，且有(i，j)∈A；r，k为多式联运网络中的运输方式标号，且有r，k∈S；Ni-为节点i的前向节点集合，且有Ni-⊆N；Ni+为节点i的后向节点集合，且有Ni+⊆N；Si为连接节点i的运输方式的集合，且有Si⊆S；Sij为有向弧(i，j)上的运输方式的集合，且有Sij⊆S；dijk为有向弧(i，j)上运输方式k的运输距离，km；tijk为有向弧(i，j)上运输方式k的运输时间，h；tirk为集装箱在节点i由运输方式r中转至运输方式k的单位中转时间，h/TEU；[φimin，φimax]为节点i的固定作业时间窗，若节点i不存在固定作业时间窗，则可将[φimin，φimax]设为[0，+∞]；cijk为有向弧(i，j)上运输方式k的单位运输费用，元/TEU；cirk为集装箱在节点i由运输方式r中转至运输方式k的单位中转费用，元/TEU；M为极大正数；

（2）变量。xijk为0-1 变量，若集装箱由运输方式k由节点i运到节点j，则xijk= 1，否则xijk= 0；yirk为0-1 变量，若集装箱在节点i由运输方式r中转至运输方式k，则yirk= 1，否则yirk= 0；zi为非负变量，表示集装箱到达节点i的时刻；wi为自然数变量，用于将zi转化为属于0 : 00 至24 : 00 之间的时刻；Δ1为非负变量，表示集装箱较运输时限时间窗下界提前到达运输终点的时间，h；Δ2为非负变量，表示集装箱较运输时限时间窗上界延迟到达运输终点的时间，h。

1.2.2 双目标混合整数线性规划模型

在参考以往优化建模[2]的基础上，以提高多式联运的经济性及时效性为优化目标，以“点-弧”模型为参考，构建集装箱多式联运路径优化模型。

（1）经济性目标函数Obj1。

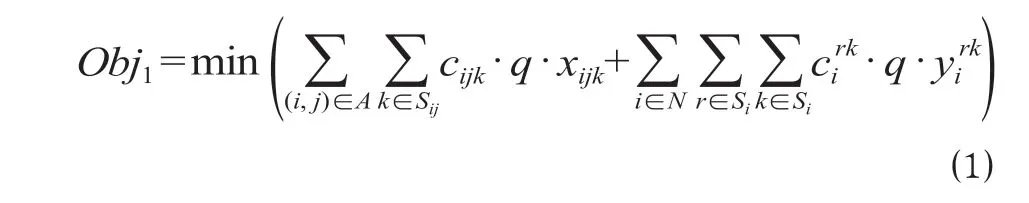
多式联运包括有向弧上的运输过程和节点上的中转过程，相应地，完成集装箱运输的费用包括在途运输费用和中转作业费用。据此，构建如式(1)所示的经济性目标函数，即完成集装箱从起点到终点运输的费用最小化。

（2）时效性目标函数Obj2。

同前所述，在组织多式联运进行长距离运输时，运输时效性也是多式联运经营人关注的重点。为了提高运输的准时性，避免集装箱过早或过晚到达终点，构建了如式(2)所示的时效性目标函数，即集装箱运抵终点的提前时间或延迟时间最小化。

（3）约束条件。

约束条件(3)为多式联运网络中的流量平衡约束，保证规划多式联运路径由起点经中转节点到终点的连续性。约束条件(4)和(5)为集装箱的完整性约束，前者保证一批集装箱在运输过程是不可分割的，后者则保证集装箱在节点中转过程中的不可分割。约束条件(6)和(7)为多式联运路径上中转节点与运输弧段接续的连续性约束，保证多式联运运输过程和中转过程的合理衔接，保证“点-弧”建模的合理性。约束条件(8)假设集装箱到达起点的时刻等于其运输开始时刻，从而进一步计算集装箱到达各个节点的时刻。约束条件(9)和(10)为变量的计算兼容性约束，计算集装箱到达规划路径上各个节点的时刻。约束条件(11)和(12)为节点固定作业时间窗约束，要求集装箱到达节点的时刻必须在规划的时间窗内，从而保证后续中转作业的顺利进行。由于节点固定作业时间窗的上界和下界均为24 小时制，因此，集装箱到达节点的时刻需首先按照约束条件(13)和(14)进行处理，使其转化为属于0 : 00 至24 : 00 之间的时刻。上述约束能够有效提升多式联运路径优化方案的合理性，确保集装箱到达某一中转节点时，该节点能快速进行集装箱的中转，从而避免集装箱在中转节点的无效等待，提高多式联运效率。约束条件(15)和(16)为变量的计算兼容性约束，分别计算了集装箱运抵终点的提前时间和延迟时间。通过设定目标函数(2)与约束条件(15)和(16)，多式联运路径优化方案能有效提高集装箱到达终点的准时性，既避免了集装箱提早到达而导致额外仓储保管等成本，又避免了集装箱延迟到达而导致客户无法按照计划完成后续生产加工等活动。约束条件(17)至(23)为变量的取值约束。

据此，构建了考虑多类型时间窗的集装箱多式联运路径优化的双目标混合整数线性规划模型。相较于既有文献多构建非线性规划模型并设计启发式算法进行问题求解，所构建的优化模型更容易进行求解，可有效用数学规划软件求得问题的全局最优解。

1.3 求解方法

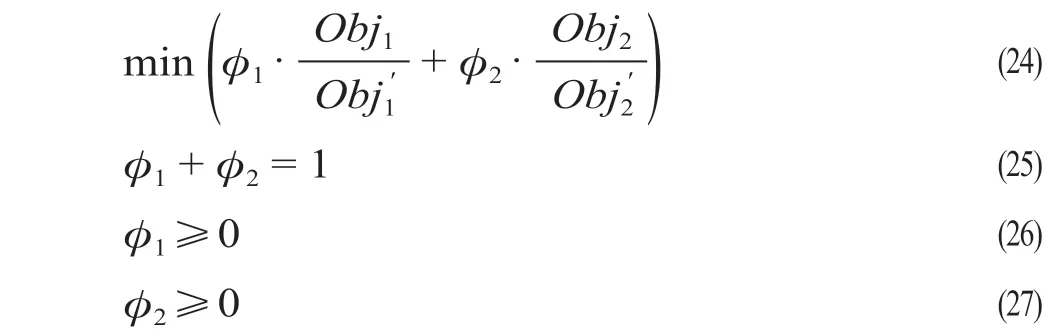
式中：ϕ1和ϕ2分别为经济性目标和时效性目标的权重，其具体取值由决策者在进行求解前人为设定。

在计算过程中，通过不断调整ϕ1和ϕ2的取值，并计算不同取值下的单目标优化模型的最优解，最终可求得问题的帕累托解。单目标优化模型的优化目标为式(24)，约束条件包括式(3)至式(23)。研究利用数学规划软件LINGO 运行分支定界算法求解单目标混合整数线性规划模型的全局最优解。

2 算例分析

为验证优化建模方法的可行性，设计了以下算例，同时对算例优化结果进行分析。集装箱多式联运路径网络如图1 所示。集装箱多式联运网络运输时间、运输距离参数如表1 所示。

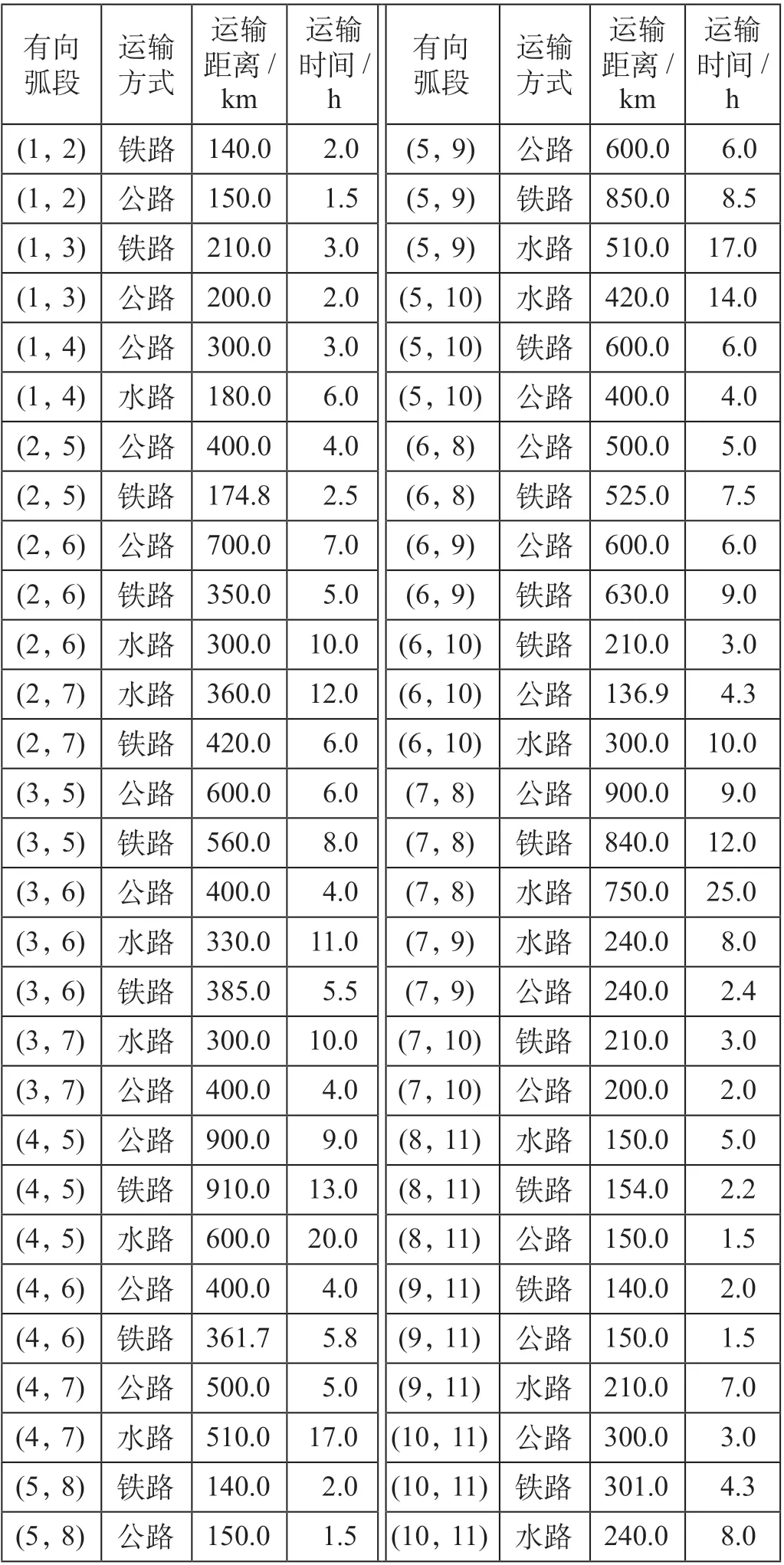
表1 集装箱多式联运网络运输时间、运输距离参数Tab.1 Time and distance for online transportation in container multimodal transportation

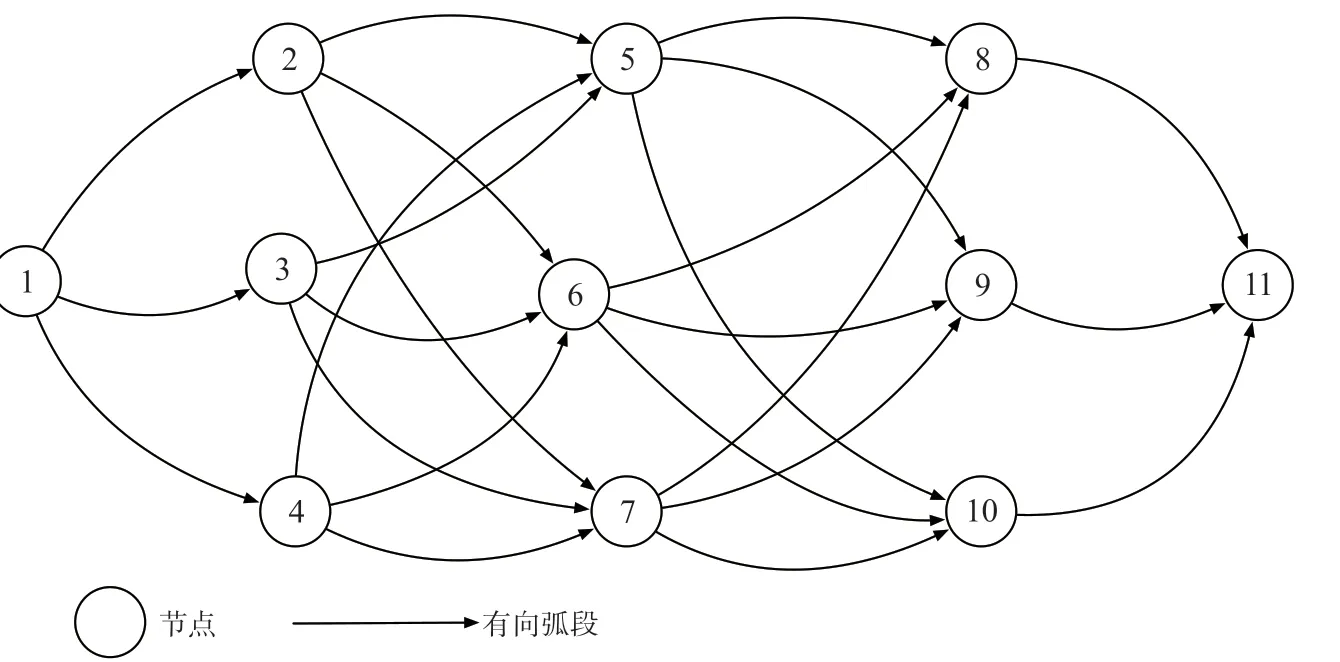
图1 集装箱多式联运路径网络Fig.1 Routing network of container multimodal transportation

在多式联运网络中，中转节点固定作业时间窗如表2 所示。

表2 中转节点固定作业时间窗Tab.2 Fixed operation time windows of transshipping nodes

不同中转方式的单位时间和费用如表3 所示。研究认为相同运输方式之间不需要中转，因此相关单位中转时间和中转费用均为0。

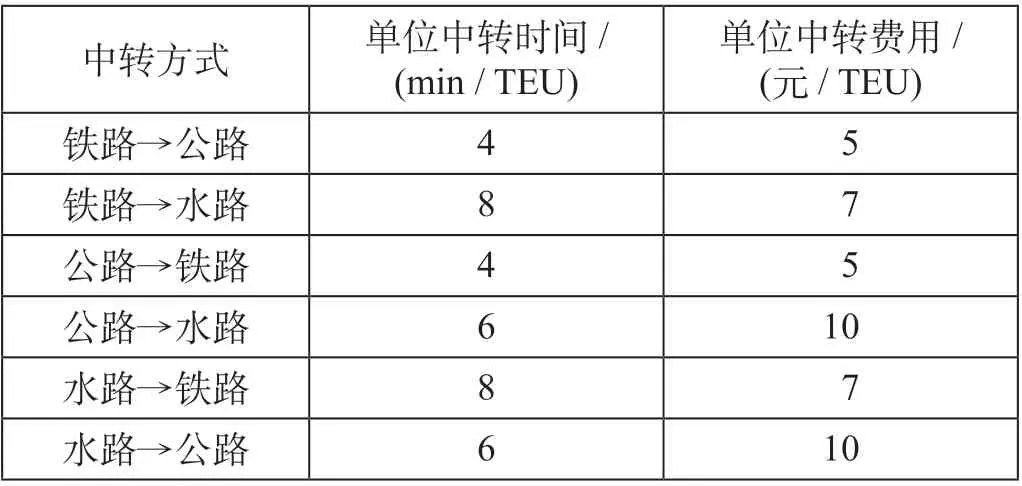
表3 不同中转方式的单位时间和费用Tab.3 Unit time and cost of different transshipping modes

在多式联运中，不同的运输方式有不同的运费计算方式。根据文献[10]中的数据计算不同运输方式的单位运输费用(单位为元/TEU)。

在算例中，假设一批集装箱需要从节点1 (起点)运输至节点11 (终点)，其运量为30 TEU，在节点1 的运输开始时刻为第1 天6 : 00，在节点11的运输时限时间窗为第2 天21 : 00 至第3 天2 : 00，也即运输时限时间窗为[45，50]。根据上述设计，利用LINGO 软件运行分支定界算法对集装箱多式联运双目标优化问题进行求解，得到集装箱多式联运路径优化问题的帕累托解如图2 所示。

图2 中的4 个帕累托解分别代表一种集装箱多式联运路径优化方案，不同优化方案具有不同的经济性目标和时效性目标。图2 所示的最优集装箱多式联运路径优化方案如表4 所示。较采用方案4，方案3 能够将多式联运的时效性提高约75%，而仅导致多式联运的经济性降低约4.7%。由图2 和表4 可知，集装箱多式联运路径优化的经济性目标和时效性目标是互相矛盾的，无法同时达到最优，提高多式联运的经济性势必以牺牲其时效性为代价，反之亦然。因此，多式联运经营人需要对多式联运的经济性目标和时效性目标进行折中处理。

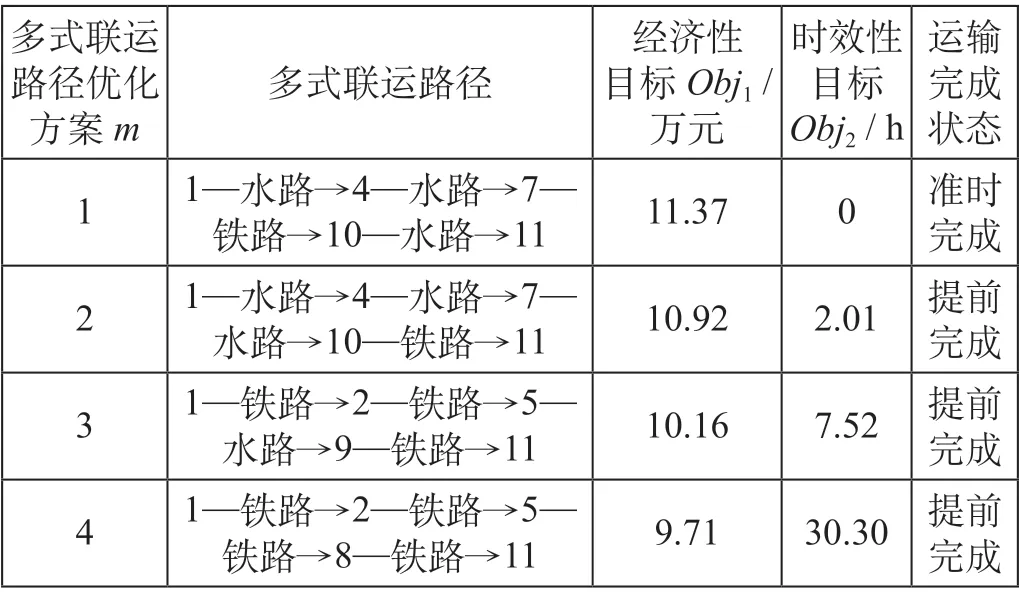
表4 最优集装箱多式联运路径优化方案Tab.4 Optimal routing scheme for container multimodal transportation

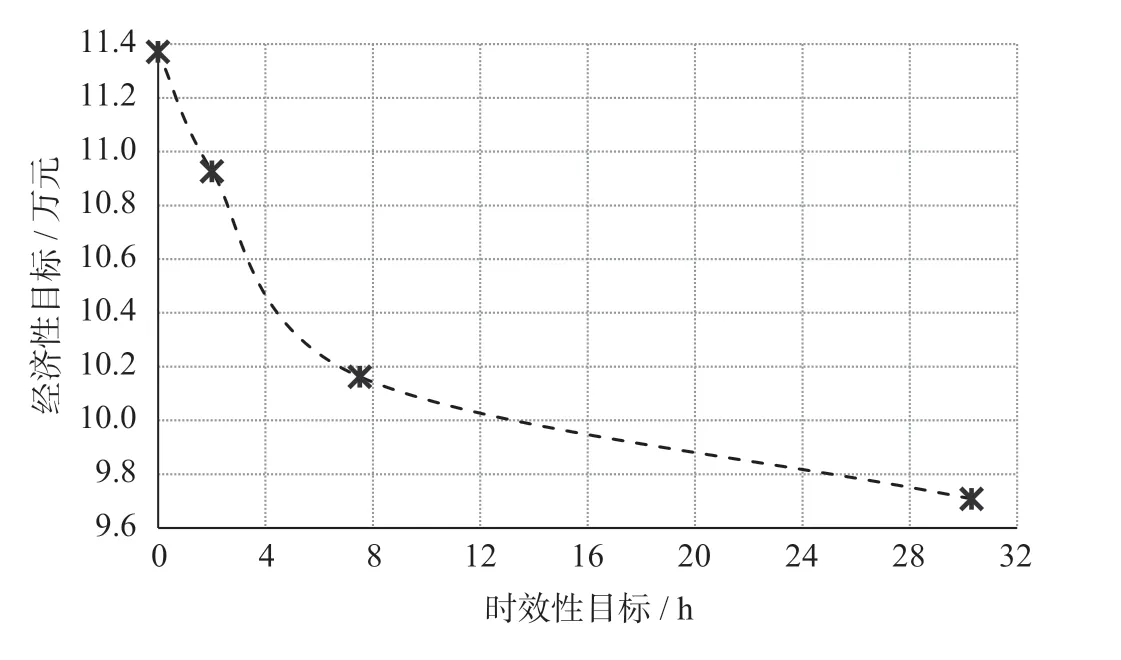
图2 集装箱多式联运路径优化问题的帕累托解Fig.2 Pareto solutions to the routing problem of container multimodal transportation

当客户十分重视多式联运的时效性，期望集装箱能够准时运抵终点，且能够接受较高的运输费用时，路径优化方案1 最为合适。如果客户对多式联运经济性和时效性同等重视，则具有均衡解的路径优化方案最为合适。对于所研究的算例，具有均衡解的路径优化方案满足式(29)所示条件。经过计算，路径优化方案3 为均衡解方案，满足客户对多式联运经济性和时效性的同等重视。

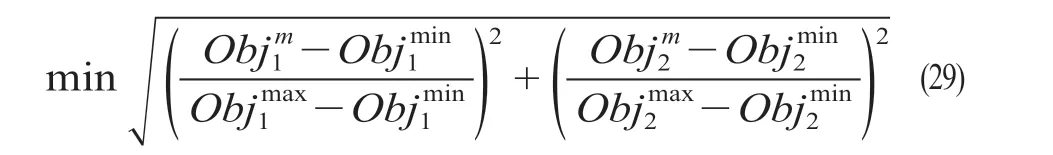
综上所述，图2 所示的每个帕累托点均代表了不同客户需求下的最优多式联运路径优化方案。在运输实践中，多式联运经营人可以结合具体的客户需求、货物时间价值等多种因素选择最为合适的集装箱多式联运路径优化方案。算例研究表明，所构建的多式联运路径优化模型可以规划多样化的多式联运路径优化方案以满足不同的客户需求，具有一定的可行性。

3 结束语

对考虑多类型时间窗的集装箱多式联运路径优化问题进行研究，规划节点的固定作业时间窗硬约束以提高路径优化的可行性，构建运输时限的软时间窗以提高规划路径的时效性。研究以降低多式联运费用和提高多式联运准时性为优化目标构建了双目标混合整数线性规划模型，采用标准化加权求和法转化为单目标优化模型，并利用数学规划软件进行问题求解。算例研究表明，集装箱路径优化问题的经济性目标和时效性目标是互相矛盾的，两者无法同时达到最优，问题优化存在帕累托解。根据问题优化结果，多式联运经营人可以根据客户在经济性和时效性上的偏好选择合适的帕累托解设计多式联运路径方案。