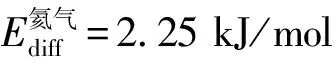氦气在氢气-空气云团中等温与不等温扩散的分子动力学模拟

杨智慧，张慧，陈威

(1.航天低温推进剂技术国家重点实验室，北京 100028；2.中国航天科技集团有限公司氢能工程技术研发中心， 北京 100074；3.北京航天试验技术研究所，北京 100074；4.苏州大学能源学院，江苏 苏州 215006)

液氢是一种热值高、来源广和可再生的环保型二次能源。液氢的黏度极小，而泄露速度反比于黏度，因此液氢很容易发生泄漏。而液氢一旦发生泄漏，就会迅速发生相变，形成爆炸范围很广(氢气体积分数在4%～75 %)的可燃性氢气-空气云团，遇热源、明火等极易导致爆燃和爆轰等危害的发生[1]。

美国国家航天局(NASA)于1980年在白沙实验基地进行大规模液氢蒸发实验，结果表明液氢池会剧烈沸腾并迅速向上发展成可燃性氢气云团[2]。王青松[3]和张起源[4]等对液氢危险性进行了研究分析，指出液氢极易泄露且泄露后会与空气混合形成可燃性的云团。

因此，液氢发生泄漏后，采用扩散系数高的氦气稀释和惰化可燃性氢气-空气云团，来降低氢气-空气云团的危害性具有一定的研究价值。本文使用分子动力学的方法，在微观层面上模拟了氦气在氢气-空气云团中的扩散，对于掌握氦气在氢气-空气云团中的扩散机理和保障氢能安全具有重要的意义。

1 模型和方法

1.1 模型构建

1.1.1 等温模型

本文考虑了氢气-空气云团扩散、氦气扩散以及两者混合扩散三种等温扩散模型，粒子随机生成在立方模拟盒子中，模拟盒子采用周期性边界条件，以模拟气体泄漏后粒子的布朗运动状态。模拟体系采用正则(NVT)系综，前2 ns用于平衡演化，后8 ns用于数据统计，时间步长为0.1 fs。

对于氢气-空气云团扩散模型，图1为氢气-空气云团扩散模型的粒子示意图。模拟中使用langevin控温方法，分别设置300 K、250 K、200 K、150 K、125 K和100 K六组不同温度进行模拟，不同温度下的系统，根据理想气体状态方程，随温度相应改变立方模拟盒子的尺寸，以维持不同温度下模拟过程中压力恒定为0.1 MPa。为了模拟实际情况下氢气泄漏后氢气-空气的混合物，氢气-空气云团中粒子数比例为H2∶空气=9∶1(空气中N2∶O2=4∶1)。对于氦气扩散模型，模拟体系只包含一定数量的氦气分子，压力、温度和模拟盒子尺寸与氢气-空气云团模型一致。

图1 氢气-空气云团扩散模型的粒子示意图

对于氢气-空气云团和氦气等温混合扩散模型，设置体系中粒子数为600，在保证H2∶空气=9∶1不变的条件下，往模拟盒子中添加氦气分子，使氢气体积分数从90 %降低至75 %、50 %、25 %和4 %，图2是氢气体积分数为50 %时，氦气在氢气-空气云团中扩散模型的粒子示意图。在氢气的四种体积分数下，再分别设置300 K、250 K、200 K和150 K四种温度，统计氦气在不同的氢气体积分数和温度下的扩散系数。

图2 氦气在氢气-空气云团中扩散模型的粒子示意图

1.1.2 不等温扩散模型

ISA95标准定义了企业商业系统和控制系统之间的集成，主要可以分成三个层次，即企业功能部分，信息流部分和控制功能部分[5]。企业功能基于Pursue大学当初建立的CIM功能模型；信息流部分基于Pursue大学的数据流模型图和S88批次标准，包括产品定义、生产能力、生产计划和生产性能4种信息流；而其控制功能则基于Pursue和MESA的功能模型[6]。

液氢泄露迅速相变后的实际温度较低，与喷入的氦气存在一定温差，因此本文研究了温差对于不等温体系扩散系数的影响。在不等温模型中，保证模拟盒子一侧氦气初始温度为300 K，改变盒子另一侧H2+空气体系的初始温度为280 K(或者260 K、240 K和220 K)，体系中粒子数为600，选取氢气体积分数占比为50 %的体系来进行研究，即体系中He∶H2∶空气=267∶300∶33。进行不等温扩散模拟，其余模拟条件设定与等温模型相同。

1.2 分子动力学设置

模拟体系中粒子为不带电的硬球模型，即库仑力的作用可忽略，因此采用短程的Lenard-Jones(简称LJ)势函数来表达气体分子之间的相互作用。LJ势函数如公式(1)所示[7]：

(1)

(2)

(3)

表1 不同气体的相互作用势参数

对于扩散系数的计算，本文基于Mean Square Displacement(MSD)法和Einstein方程来求解扩散系数，MSD的表达式为[8]：

(4)

式(4)中，N为体系中的粒子数，r(0)为初始时刻粒子位置，r(t)为t时刻粒子对应的位置。结合Einstein方程：

(5)

式(5)中，D是扩散系数，单位为m2/s，可以由MSD随时间变化曲线的斜率得到，则扩散系数D与MSD之间的关系可表示为：

(6)

2 模拟结果分析

2.1 等温扩散

图3和图4分别展示了等温条件下氢气-空气云团和氦气扩散的MSD-t随时间的变化。从图3和图4中可以看出，随着时间的增加，两种体系中气体的MSD逐渐增大，且均随时间呈线性变化。氢气-空气云团和氦气两种体系的气体分子间除相互作用外不受任何外力，在温度从100 K增大到300 K的过程中，模拟体系压力恒定，故气体分子平均自由程和碰撞频率增大。温度与动能的关系如公式(7)所示：

(7)

式(7)中，mi和vi分别为粒子i的质量和速度，N为体系中的粒子总数，kB玻尔兹曼常量，T为体系的温度，即随着温度升高，分子平均动能也越大，在相同的时间内，分子运动的距离越远，MSD曲线的斜率越大。即随着温度升高，分子平均动能也越大，在相同的时间内，分子运动的距离越远，MSD曲线的斜率越大。

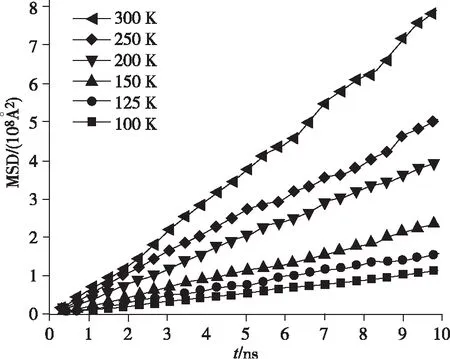
图3 氢气-空气云团扩散的MSD-t变化图

图4 氦气扩散的MSD-t变化图

表2 不同温度下氢气-空气云团和氦气的扩散系数

表3中展示了在不同的温度和氢气体积分数下，氦气在氢气-空气云团中的扩散系数。由表3可以得出，随着温度的增加，分子的平均动能增大，扩散系数随之增大；在相同温度下，随着氢气体积分数的降低，体系中气体分子的扩散逐渐从以氢气-空气云团为主变成以氦气为主，氦气的扩散能力高于氢气-空气云团，因此氦气在氢气-空气云团中的扩散系数增加。

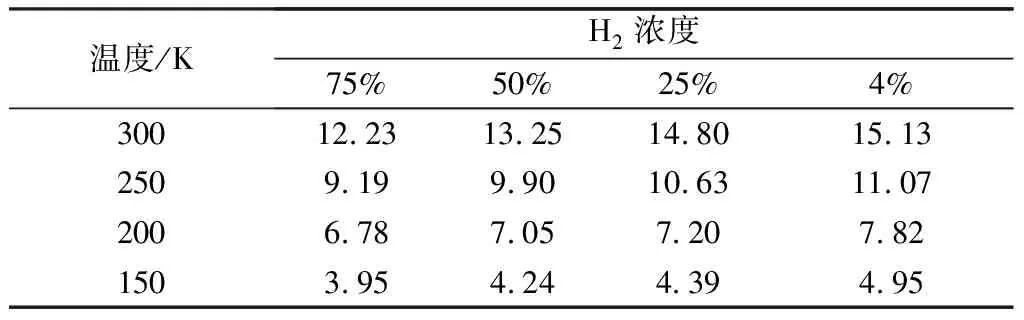
表3 氦气在氢气-空气云团中的扩散系数10-5m2·s-1

2.2 不等温扩散

图5为不同温差下氦气在氢气-空气云团中扩散系数的时间演化图。从图5中可以看出，在前2 ns，扩散系数随时间迅速增加，在2～10 ns中，四种不等温扩散体系(氦气温度固定为300 K，氢气-空气云团温度分别为280 K、260 K、240 K和220 K)的扩散系数处于动态平衡中。对于普通气体分子扩散，开始的一段时间内MSD是时间的二次函数，代表无障碍的定向扩散，随着扩散时间的增加，MSD会过渡到一次函数阶段，代表正常扩散[9]，因此扩散系数会先迅速增加后稳定。

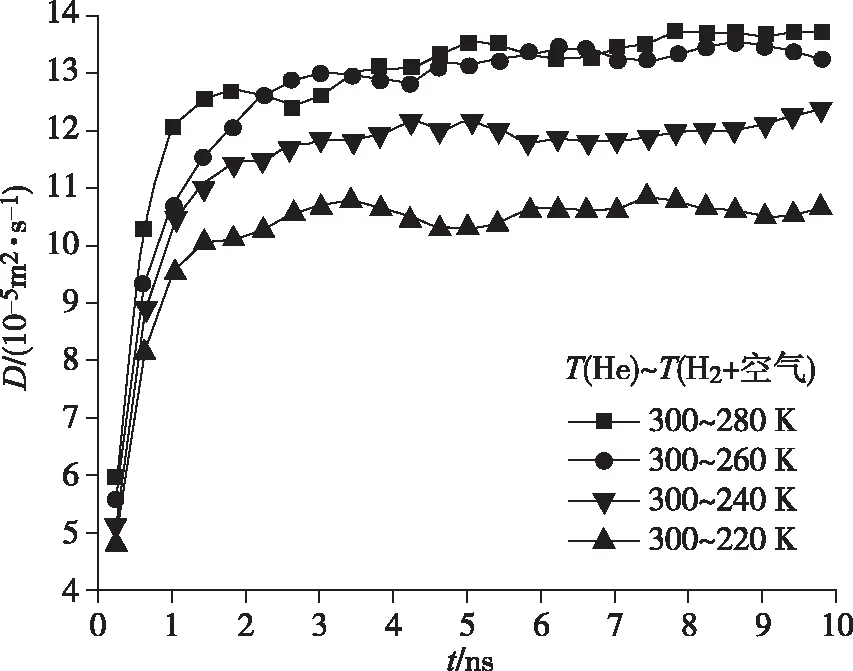
图5 不同温差下氦气在氢气-空气云团中扩散系数的时间演化图

本文对于扩散系数的统计选取2～10 ns正常扩散阶段的数据，从图5中分析得知，温差越大的体系，由于分子之间进行能量交换后的平衡温度更低，体系具有的平均动能也相应更低，氦气在氢气-空气云团中的扩散系数相应的更小。

2.3 Arrhenius方程

JUAN J S等[10]通过对大量气体分子扩散的研究，发现扩散通常和温度有着强烈的依赖性。扩散系数和温度相关性通常服从公式(8)所示的Arrhenius方程[11]：

(8)

式(8)的自然对数形式为：

(9)

式(9)中，D为扩散系数，D0为指前因子，Ediff是扩散活化能，R是气体常数(取8.314 J/molK)，T是绝对温度。扩散活化能Ediff和指前因子D0可由式(9)中1nD和T-1的拟合直线求得。

图6展示了100～300 K 时氢气-空气云团和氦气扩散的Arrhenius图，通过拟合直线可以分别求出在100～300 K的温度范围中，氢气-空气云团和氦气扩散系数的表达式为：

图6 氢气-空气云团和氦气扩散的Arrhenius图

图7展示了100～300 K时氦气在氢气-空气云团中扩散的Arrhenius图，由拟合直线求得氦气在氢气-空气云团中的的范围为2.75～2.99 kJ/mol，四种体系中氦气扩散活化能相近，表明氦气在这些体系中的扩散能力的差别较小。

3 结语

本文采用分子动力学模拟分别计算了氦气和氢气-空气云团的扩散系数，并研究了氦气在氢气-空气云团中等温和不等温的扩散机理。主要结论如下：

(1)温度和氢气体积分数对氦气和氢气-空气云团扩散系数有显著影响。在0.1 MPa的模拟条件

图7 氦气在氢气-空气云团中扩散的Arrhenius图

下，氦气在100～300 K的温度范围内扩散系数均高于同温度下的氢气-空气云团。对于氦气在氢气云团中的等温扩散，随着温度的升高，氦气扩散系数增大；氢气体积分数较高时，体系中以氢气-空气扩散为主，而氢气体积分数较低时，氦气的扩散占据主导。

(2)氦气和氢气云团的不等温扩散，气体分子由定向扩散过渡至正常扩散时，MSD与时间的二次函数关系会过渡到一次函数阶段，扩散系数出现先增大后稳定的现象。