高炉喷吹用兰炭与煤粉非等温/等温燃烧热分析动力学研究*

2022-07-14何江永赵俊学任萌萌

煤炭转化 2022年4期

何江永邹冲赵俊学任萌萌李玺俞楠

(西安建筑科技大学冶金工程学院，710055 西安)

0 引言

在碳中和、碳达峰的大背景下，以中低温热解技术为核心的低阶煤梯级分质利用技术可将低阶煤转化为煤气、焦油和兰炭三种能源形式，是实现低阶煤清洁、高效、多层次转化利用的重要途径。兰炭作为低阶煤热解终端的主要固体产物，目前全国产能已达1.2亿t。由于高炉喷吹煤粉的需求量巨大，仅一年喷煤需求量就超过1亿t，同时高炉喷吹用优质无烟煤资源短缺、价格高昂，较多的学者和企业进行了高炉喷吹兰炭的研究和实践[1-3]。兰炭除具有固定碳含量高、挥发分含量低、发热量高的特点外，还具有灰分含量低及有害元素S，P含量富集少等优点。然而，研究[4-5]发现与喷吹煤粉相比，兰炭在用于高炉喷吹替代燃料时存在燃烧性能不足或性能波动较大的缺点，这可能导致炉况恶化、燃料利用率降低等问题。燃料的燃烧性能除与自身属性有关外，燃烧的动力学环节同样是十分重要的影响因素，研究兰炭和喷吹煤粉等温燃烧动力学和非等温燃烧动力学之间的异同，对实现兰炭在高炉喷吹中的应用具有重要的指导意义。

热分析(非等温燃烧、等温燃烧)方法被诸多研究者认为是研究煤燃烧行为的有效方法[6-9]。非等温燃烧能在连续升温下监测燃料的自发着火和后续燃烧过程；等温燃烧具有初始燃烧温度与高炉喷吹环境温度接近的优势，因此，两种方法均被广泛采用[7，10]。非等温燃烧、等温燃烧的动力学参数对评价燃料燃烧性能至关重要，活化能表示了燃料燃烧过程中所需越过的能垒，机理函数则体现了燃料在不同动力学环节下的限制性环节。非等温燃烧活化能的计算最常用的、认可度最高的方法是等转化率的方法，包括FOW方法、KAS方法、Starink方法[10-12]等，这些方法可以避免机理函数的选择对活化能的计算产生影响。尽管采用等转化率的方法具有特定优势，但是HU et al[10]采用不同等转化率的方法计算活化能时发现，在活化能求取过程中，拟合直线的相关系数存在差异，采用FOW方法时相关系数最高。机理函数的计算有双外推法[13]、Malek方法[14]、Popesuc[15]方法等，其中Malek方法可排除动力学补偿效应，被认为是可靠程度高的动力学分析方法。等温燃烧动力学参数的求取主要采用模式配合法，需要对可能的机理函数进行逐一尝试，在得到机理函数表达式之后进一步对活化能进行求解。尽管针对非等温/等温燃烧的动力学计算的应用较为成熟广泛，但由于不同的方法求得的反应机理和动力学参数相差较大，至今还没有形成完整可靠的求取兰炭和喷吹煤粉燃烧各阶段动力学模型的方法，也缺乏两种条件下动力学参数和机理模型的比较研究，尤其是在以兰炭代替喷吹煤粉过程中，两种方法下的动力学求取结果是否有可比性目前尚无相关报道。因此，有必要对兰炭和高炉喷吹煤粉燃烧的燃烧特性及动力学机理作深入的解析研究，明确兰炭和喷吹煤粉动态燃烧特性及机理的差异性。

本研究首先采用热分析仪对兰炭和喷吹煤粉在非等温/等温燃烧条件下的燃烧特性进行了分析；其次，利用等转化率的FOW方法对非等温燃烧的活化能进行了求解，并进一步采用Malek方法对非等温燃烧过程的机理模型进行了解析；再次，对等温燃烧的动力学参数采用模式配合的方法进行了求解；最后，对样品非等温/等温燃烧特性、动力学参数(机理函数模型、活化能)之间的差异进行了对比分析。

1 实验部分

1.1 实验原料

实验所用两种兰炭取自一家高炉喷煤制粉车间，两种喷吹煤粉取自两家炼铁厂制粉车间，所选取的四种样品的D50分别为：Char 1#168.64 μm，Char 2#17.58 μm，Coal 1#23.85 μm，Coal 2#41.09 μm；对应样品的工业分析和元素分析见表1。样品使用前利用烘箱在105 ℃条件下对其进行4 h烘干处理。由表1可知，就挥发分和固定碳而言，Char 1#和Coal 1#接近，Char 2#和Coal 2#接近。

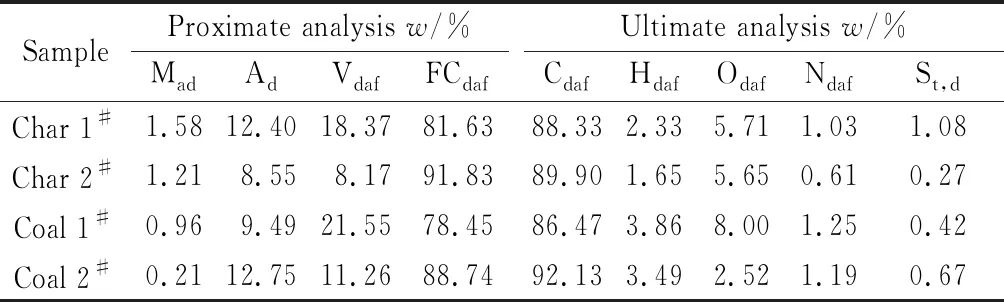
表1 样品的工业分析和元素分析Table 1 Proximate and ultimate analyses of samples

1.2 燃料燃烧性能表征方法

样品非等温/等温燃烧均在热分析仪(SETSYS Evolution，France，SETARAM)上进行。

非等温燃烧：将(10±0.1) mg样品置于φ3 mm×5 mm的石英坩埚中，并置于热分析仪的加热炉腔中，在50 mL/min的空气气氛下分别以5 ℃/min，10 ℃/min，20 ℃/min的升温速率升温至确保样品能燃尽的终止温度900 ℃。为了消除炉腔内气体流动对结果的影响，在室温下静置保温10 min，随后开始实验。样品燃烧反应性借助燃烧特征参数进行评价，采用TG-DTG法获取；燃烧特征参数包括着火温度(θi)、燃尽温度(θf)、燃烧过程失重量达到98%时的温度、最大燃烧速率对应的温度(θm)、可燃性指数(C)和燃尽指数(Df)。

可燃性指数(C)表征着火后继续燃烧特性，值越大，样品的可燃性越好。

(1)

燃尽指数(Df)表征燃料燃尽特性，值越大，表示燃尽性能越好。

(2)

式中：(dw/dt)max为最大燃烧速率，tm和tf分别为θm和θf所对应的时间。

等温燃烧：样品的用量及坩埚类型与非等温燃烧实验时一致，二者显著的区别在于等温燃烧在坩埚置于加热炉腔后需借助真空泵将炉腔抽成完全真空的状态，而后通入高纯氩气，其目的是保护炉料在达到预设温度之前不被氧化，随后在氩气气氛下以50 ℃/min的升温速率迅速达到预设温度1 000 ℃，1 100 ℃，1 200 ℃，并保温10 min以确保炉温和样温同步，保温结束后切换成50 mL/min空气气氛进行燃烧实验，等温燃烧反应特性用反应性指数RS(RS=0.5/t0.5)来评价，其中t0.5表示转化率达到50%时对应的时间；RS值越大，表示其反应性越好。

1.3 动力学计算及模型的建立

非等温燃烧反应的动力学方程可表示为：

(3)

(4)

式中：A为指前因子，s-1；Ea为活化能，kJ/mol；R为气体摩尔常数，R=8.314 J/(mol·K)；f(α)为机理函数；T为反应温度，K；α为转化率(其中m0为初始质量，g；mt为反应至t时的质量，g；m∞为反应结束时的质量，g)。

本研究中非等温燃烧活化能的计算选取等转化率的FOW方法[10，16]，表达式为：

(5)

式中：β为升温速率，K/min；Ea为活化能，kJ/mol；R为气体摩尔常数，R=8.314 J/(mol·K)；A为指前因子，s-1；G(α)为机理函数；Tα为转化率为α时对应的温度，K。

非等温燃烧过程的机理函数通过Malek方法确定，Malek方法的最大优势在于排除了模式函数和动力学补偿效应的影响，使得所求机理函数的可靠程度更高，同时可避免常规分析中机理函数一一尝试的繁琐步骤，极大地减少动力学机理函数求取过程中的工作量。具体的确定方法是将实验曲线y(α)与标准曲线对应的y(α)作对比，初步确定可能的机理函数；随后将实验曲线Z(α)与标准曲线对应的Z(α)进行对比验证，从而得到最终所求机理函数。

等温燃烧反应的动力学方程可表示为：

(6)

采取模式配合法将速率常数和机理函数分离，进一步通过两步配合来获取所需动力学三因子。首先，在一条等温的α-t曲线上选取一组α，t代入用来尝试的G(α)中，G(α)-t图为一条直线，斜率为K，选取能令直线最佳的G(α)作为最终确定的机理函数；随后用类似的方法确定不同温度下的K值，由lnK=-E/RT+lnA可知，作图lnK-1/T可得一条直线，由其斜率可获得E值。

表2所示为气-固等温燃烧、非等温燃烧过程中可能发生的动力学机理模型[17]，包括扩散、反应级数、化学反应、收缩核模型和随机核模型等。

表2 典型动力学机理函数Table 2 Typical kinetic mechanism functions

2 结果与讨论

2.1 非等温燃烧特性分析

样品在不同升温速率下的转化率和转化速率的变化如图1所示，燃烧特征参数见表3。由图1可知，随着升温速率的加快，样品燃烧的热滞后效应越来越明显，因此使得燃烧温度区间变宽。结合不同升温速率下达到最大反应速率时对应的转化率可知，两种兰炭在升温速率为10 ℃/min时达到最大反应速率，此时对应的转化率最高；煤粉则在升温速率为5 ℃/min时达到最大反应速率，此时对应的转化率最高，且随着升温速率的升高，达到最大反应速率时对应的转化率降低。这一结果表明煤粉在低升温速率下更容易快速燃烧转化，兰炭则可以在相对较高的升温速率下达到快速燃烧转化的目的。

由表3可知，不同样品燃烧特征参数存在较大的差异，以较具代表性的着火温度作为主要的研究指标进行分析，发现对于同一样品，着火温度随着升温速率的升高逐渐升高，主要是由于升温速率加快使得热量传输存在滞后性以及氧气分子的扩散不充分。在相同升温速率下，兰炭的燃烧特征参数并未表现显著区别于喷吹煤粉的特殊属性，挥发分含量接近且较高的Char 1#和Coal 1#的着火温度较低，其中挥发分含量高的Coal 1#的着火温度更低；挥发分含量低且接近的Char 2#和Coal 2#的着火温度较高，其中挥发分含量低的Char 2#的着火温度较低；这一现象表明挥发分必须达到一定含量才对着火温度具有明显的促进作用。

图1 样品非等温燃烧转化率-转化速率曲线Fig.1 Non-isothermal combustion conversion-conversion rate curves of samplesa—Char 1#；b—Char 2#；c—Coal 1#；d—Coal 2#

2.2 非等温燃烧动力学分析

图2所示为样品在不同转化率时的拟合直线，各转化率对应的活化能见表4。由图2可知，样品拟合直线的斜率随转化率的增大呈现出减小的变化趋势。由表4可知，活化能随转化率的提高呈现出降低的趋势，这一变化趋势与HU et al[10，18]通过三种方法(FWO方法、KAS方法和Starink方法)得出的结论相一致；然而相关系数却与其存在一定的差异，主要的原因可能是煤中挥发分的存在使得燃料的燃烧更为复杂多变，如WANG et al[11]在作相关研究时发现，高挥发分含量的煤种非等温燃烧动力学参数拟合计算过程中，相关系数的区间为0.961～0.993，与本研究中相关系数区间较为一致。

表3 不同升温速率下燃烧特征参数Table 3 Combustion characteristic parameters at different heating rates

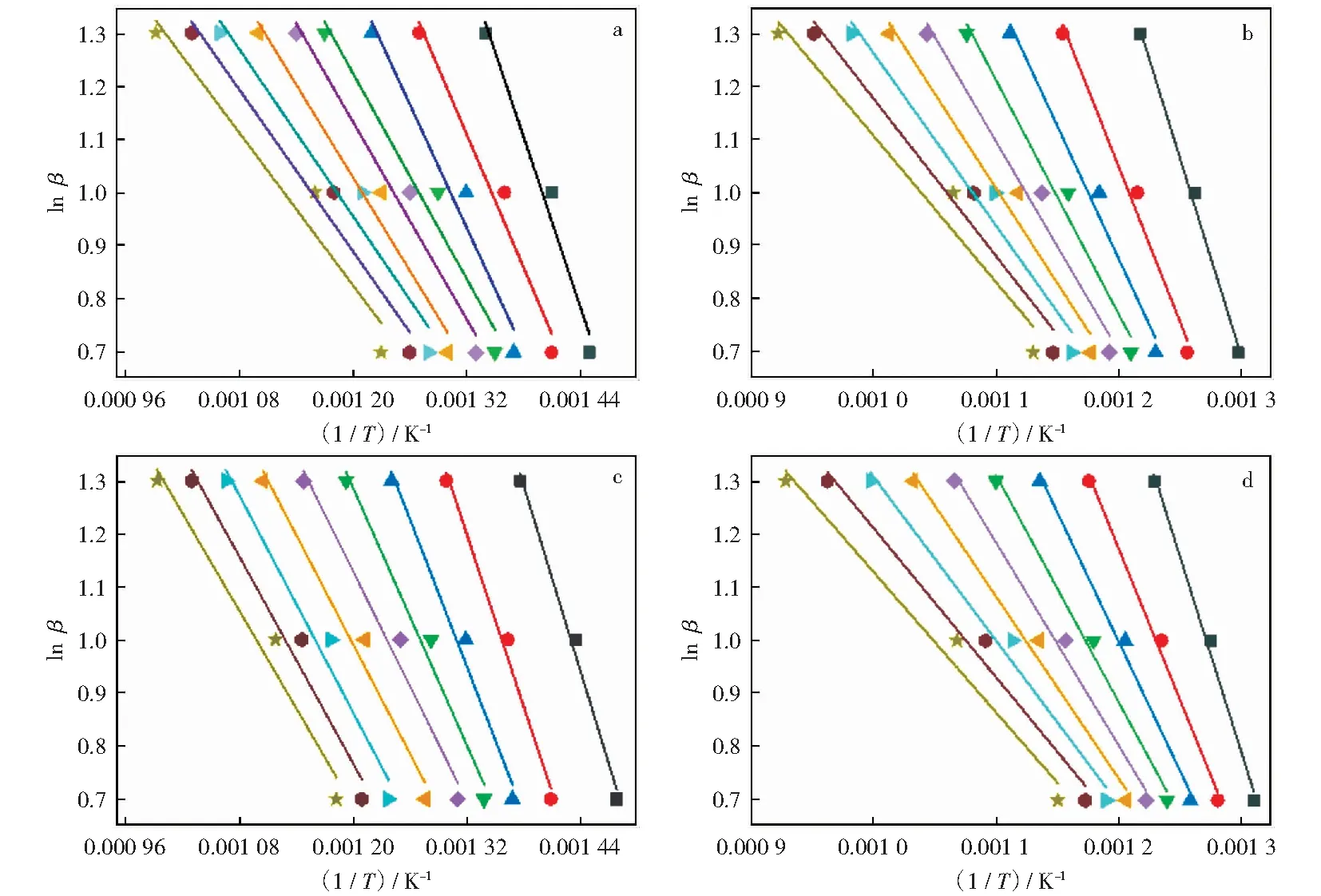
图2 非等温燃烧动力学模型拟合曲线Fig.2 Fitting curves of non-isothermal combustion kinetic modela—Char 1#；b—Char 2#；c—Coal 1#；d—Coal 2#

此外，就活化能均值而言，兰炭的燃烧更容易进行。

通过Malek方法得到的兰炭和喷吹煤粉的燃烧机理如图3所示。由图3可知，Char 1#和Coal 2#对应的燃烧机理符合n=1/4的反应级数；Char 2#的动态燃烧符合界面化学反应机理模型；Coal 1#由于自身为混煤，因此不同转化时期的机理函数存在差异，在转化前期与Char 2#机理模型一致，在转化后期则符合二维扩散的机理模型。这一结果表明尽管非等温动态燃烧机理函数形式多变，但是高炉喷吹兰炭和煤粉的燃烧机理存在共性。对兰炭和煤粉分别进行分析可知，两种兰炭和两种喷吹煤粉在相同燃烧条件下的动力学机理各不相同，这一结果说明了非等温燃烧过程中机理函数的复杂属性。

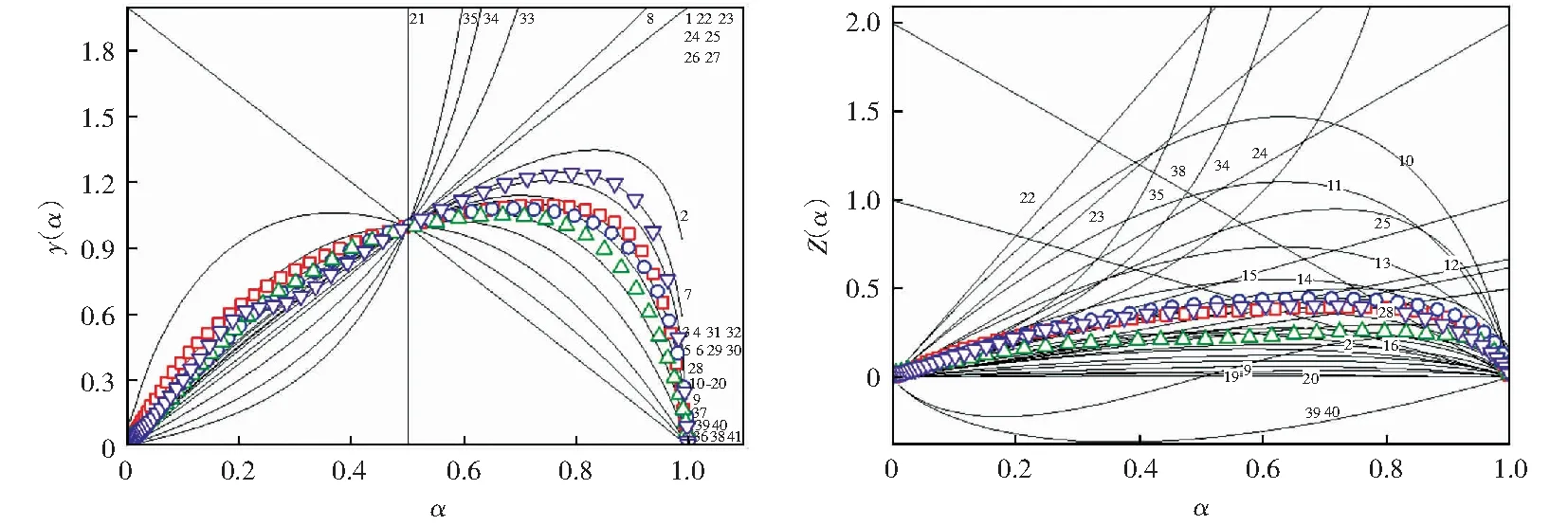
图3 标准曲线y(α)和Z(α)与实验曲线Fig.3 Experimental and theoretical y(α) and Z(α) master plots for combustion of samples

2.3 等温燃烧特性分析

图4所示为样品分别在设定温度为1 000 ℃，1 100 ℃，1 200 ℃下的α-dα/dt曲线，表5所示为样品等温燃烧反应性指数。由图4可知，随着预设温度的升高，样品燃烧的转化率曲线左移，dα/dt峰值增大，这主要是由于高温使得处于激发态的活化分子数量增加的同时分子的不规则运动加剧，二者均有利于反应的正向快速进行。对dα/dt曲线进行分析，发现在转化率逐渐增大的过程中，dα/dt曲线的峰型与幂函数y=x0.5的形状较为一致，反应速率增加幅度随转化率的升高逐渐变缓，造成这一现象的原因可能是：等温燃烧过程中，气体的扩散是主要的限制性环节，在气体切换初期，由于活化分子数量多，在接触氧气时可迅速发生反应；然而由于颗粒表面和中心存在边界问题，随着反应的进行，颗粒中心包裹的灰层厚度不断增加，使得灰层对气体扩散到达反应界面的阻力不断增大，因此，反应速率呈现出缓慢增加的趋势，甚至有样品在反应末端出现略微降低的变化。

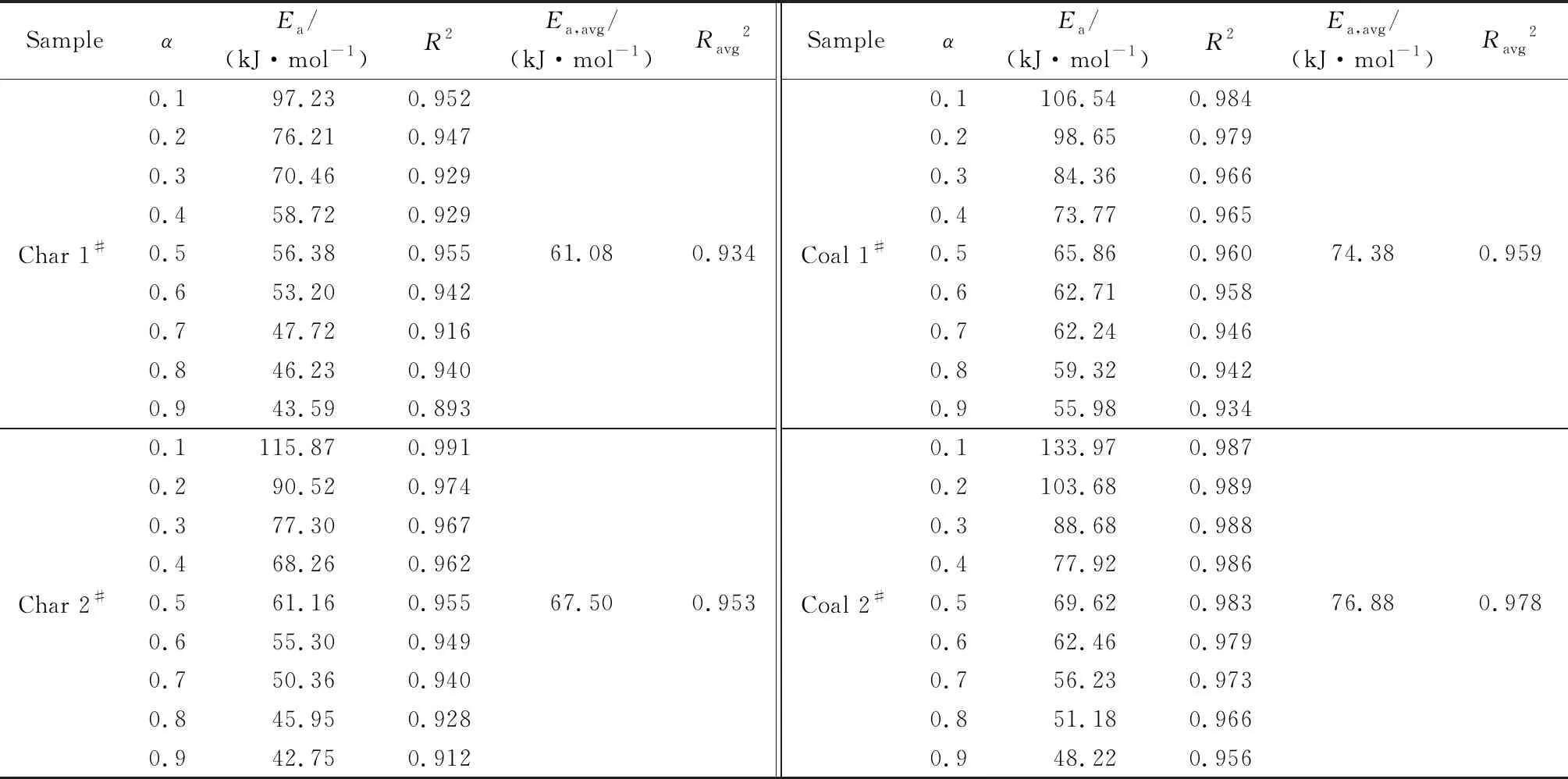
表4 非等温燃烧过程中不同转化率对应的活化能及均值Table 4 Activation energies obtained by TG data at different conversions

由表5可知，随着温度的升高，不同样品的反应性指数均增大，这表明高温有利于样品燃烧反应的快速进行，造成这一现象的主要原因是：高温使得活化分子的数量增加，同时活化分子的不规则运动加剧。此外，就相同温度下不同样品反应性指数而言，兰炭的反应性优于煤粉的反应性。

图4 样品等温燃烧转化率-转化速率曲线Fig.4 Isothermal combustion conversion-conversion rate curves of samplesa—Char 1#；b—Char 2#；c—Coal 1#；d—Coal 2#

表5 不同燃烧温度下样品的燃烧反应性指数Table 5 Reactivity indexes of samples at different combustion temperatures

2.4 等温燃烧动力学分析

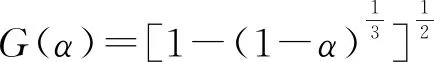
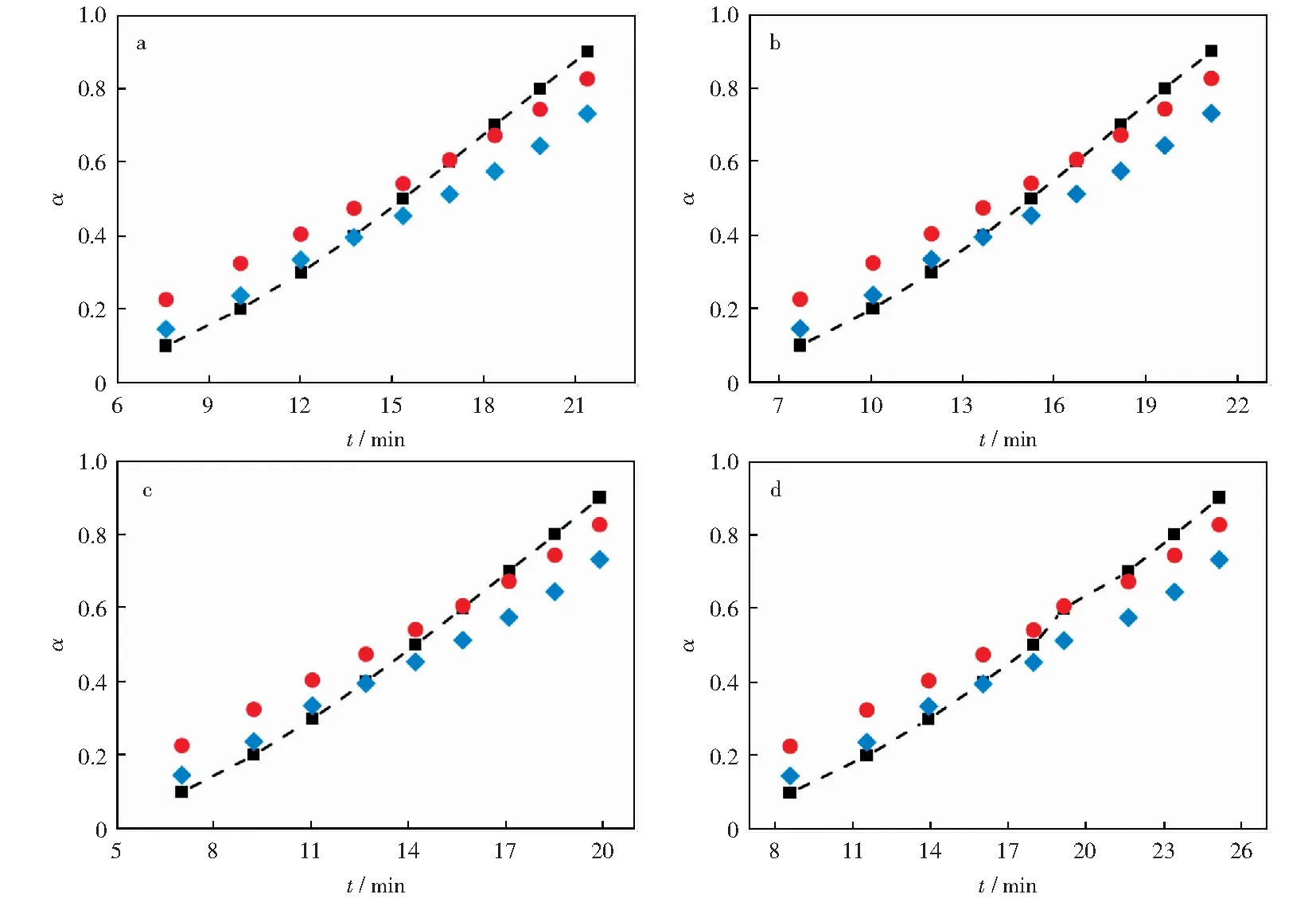
图5 样品等温燃烧实验曲线与标准机理函数曲线Fig.5 Isothermal combustion experimental curves of samples and standard mechanism function curvesa—Char 1#；b—Char 2#；c—Coal 1#；d—Coal 2#

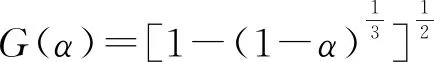
图6 样品等温燃烧动力学模型拟合曲线Fig.6 Fitting curves of isothermal combustion kinetic models of samplesa—Char 1#；b—Char 2#；c—Coal 1#；d—Coal 2#

表6 等温燃烧不同机理函数对应的活化能Table 6 Activation energies corresponding to different mechanism functions of isothermal combustion

2.5 非等温燃烧与等温燃烧动力学差异分析

图7所示为非等温燃烧条件下不同转化率对应的活化能以及采用不同机理函数对应的等温燃烧的活化能。由图7可知，在非等温燃烧条件下，随着转化率的升高，活化能逐渐降低，并趋于稳定，各转化过程的活化能均大于等温燃烧条件下采用不同机理函数得到的活化能值，WANG et al[11]在研究等温燃烧活化能和非等温燃烧活化能的差异时得到了与此一致的结论，这表明就活化能而言，等温燃烧过程更容易进行。造成这一现象的原因主要包括两个方面：一是以化学反应为限制性环节的反应本身就难以进行；二是等温燃烧预设温度更高，使得反应过程中处于激发态的活化分子数量更多，分子的运动更加剧烈，有利于促使反应正向快速进行。

图7 非等温/等温燃烧活化能Fig.7 Non-isothermal/isothermal combustion activation energya—Char 1#；b—Char 2#；c—Coal 1#；d—Coal 2#

对非等温/等温燃烧条件下燃烧机理进行对比发现，样品非等温燃烧过程的机理函数表现复杂，等温燃烧过程的机理函数则以扩散为主，表现较为单一，推测造成等温燃烧机理函数较为单一的主要原因是：达到预设温度之前对样品的高温预处理使得样品的均一性更好，这与文献[22-25]中说法一致，影响不同样品燃烧特性的孔隙结构和微晶碳化学结构在高温热处理过程中差异减小，其中孔隙结构的发达程度减弱[22]，微晶碳化学结构的排列则更加规则有序[23-25]。此外，观察发现尽管通过数学拟合计算的方式可以将非等温/等温燃烧动态演变过程用数学表达式的方式描述，但是存在标准函数曲线与实验曲线并未完全重合这一现象，在HU et al[10]的研究过程中同样存在这一类似现象；造成这一现象的原因主要是煤焦属于组成、结构复杂多变的一类非均相物质，然而在采用数学计算的方式求取机理函数时只能预设一特定的均相机理模型，无法将燃烧过程中所有的影响因素都考虑在内。

通过对兰炭和喷吹煤粉非等温燃烧动力学和等温燃烧动力学进行对比分析发现，与实际高炉喷吹工况对比而言，采用等温燃烧的方式存在一些不足之处，表现为温度的恒定不变以及到达预设温度前的高温预处理脱除了残余挥发分使得燃料开始燃烧的结构趋于一致，无法实现对原始燃料燃烧状态的准确解析。非等温燃烧的方式则与高炉喷吹实际工况存在相似性，体现在燃烧温度的动态变化，同时燃料中挥发分的促进作用也得以体现。与等温燃烧的方式相比，采用非等温燃烧的方式计算兰炭替代喷吹煤粉燃烧动力学更为合理。此外，结合兰炭和喷吹煤粉活化能和挥发分含量的关系可知，在满足高炉喷吹对发热量、火焰返回长度等指标要求的前提下，选择高挥发分含量的喷吹燃料有利于活化能的降低及燃烧性能的提高。