基于MOPSO的分布式电采暖温度范围多目标优化

王甜甜，于 非，杨玉龙

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.吉电未来智维能源科技(吉林)有限公司，吉林 长春 130000)

能源枯竭和环境污染形势日益严峻，能源转型发展和大气污染防治是当前生态文明建设工作的重点.随着环境问题的日益严重，世界范围内均在不断提高电能使用占比，由于电能的清洁性，使得大规模的电能使用可以有效缓解环境污染问题.近年来，我国“三北地区”不断推进“煤改电”工程建设.在解决北方冬季环境污染问题的同时，改进了居民生活质量，促进了能源转型[1-5].

“煤改电”措施主要以电采暖方式进行推广，对于“三北地区”的“煤改电”工程，较多采用分布式电采暖方式，分布式电采暖是传统的集中式供暖的一种补充，其在运行过程中可以直接将电能转化为热能，实现电-热能直接转化.分布式电采暖以其较大的调节、控制与保证能力被用户所接受.建筑物的储热特性使分布式电采暖负荷具有时移性.近年来，国内外学者针对分布式电采暖问题进行了大量研究，文献[6]制定了分散式电采暖负荷协同优化运行策略，提出智能电采暖网络的概念、架构以及优化指标，该策略在实现经济运行的同时，间接响应电网削峰填谷.文献[7]通过物理模型研究和负荷现场实测的方式，针对不同类型的电采暖设备所产生的谐波含量进行了差异化分析，研究了规模化电采暖设备对电网电能质量的影响问题.文献[8]利用聚类分组控制的方法实现异质电采暖负荷聚类，在此基础上建立基于风电功率预测误差区间的备用计划优化模型，并验证了备用优化模型的可行性及经济性.但目前针对分布式电采暖研究多采用恒定温度上下限(恒温限)模型进行分析，在设备实际运行过程中难以有效保证经济性及人体舒适度.

本文针对分布式电采暖设备温度上下限进行研究，首先建立分布式电采暖设备运行模型，分析环境温度影响因素.进一步，对人体舒适度模型进行简化，并建立人体舒适度评价量化指标，在此基础上，以人体舒适度及经济性为目标，建立分布式电采暖设备温度范围多目标优化模型，采用多目标粒子群算法(Multi-Objective Particle Swarm Optimization，MOPSO)求解多目标模型，并采用加权多目标决策方法确定最优解.最后，通过算例仿真，对比分布式电采暖设备恒温限及变温限结果，验证本文所提方法的有效性，为分布式电采暖设备温度范围研究与制定提供新的思路.

1 分布式电采暖运行模型

分布式电采暖设备包含直热式及蓄热式两类，本文主要针对电直热设备进行分析.由于电直热设备安装过程中综合考虑房屋结构及地区温度情况，因此针对其运行过程中房间及环境之间的热场变化特性常采用能量守恒原理建立其电-热特性关系.考虑到电采暖设备复合传热过程，常采用二阶热参数模型[9].分布式电采暖功率-环境系统等效热参数模型如图1所示.

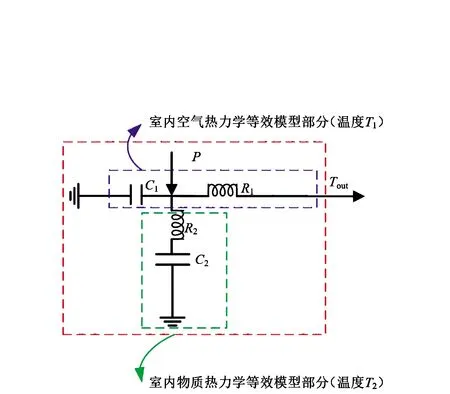
图1 分布式电采暖功率-环境系统等效热参数模型

分布式电采暖功率-环境系统热参数模型包含空气及环境物质两部分，对应温度分别为T1、T2，室外温度为Tod.对于分布式电采暖单元模型而言，其空间状态方程为：

(1)

公式中：C1、C2分别为室内空气及物质热容；R1、R2分别为室内空气及物质热阻；P为分布式电采暖设备功率.

在一定的环境温度范围内，考虑到测量过程中分布式电采暖设备的启停时间，可以进一步简化分布式电采暖单元模型，设备启停过程中，室内温度Tid变化分别由公式(2)、公式(3)计算.

(2)

(3)

公式中：Tod为室外温度；i为仿真步长，考虑到分布式电采暖设备特性及温度变化速度，本文取步长i为60秒.

2 分布式电采暖多目标模型

针对分布式电采暖恒温范围时所存在的经济性、舒适性难以保证问题，本文综合考虑舒适性及经济性问题，以一天内各时段分布式电采暖设定温度上下限为决策变量，以舒适度最优及电采暖费用最低为目标函数，建立分布式电采暖多目标模型.

2.1 舒适度目标

目前广泛采用的人体舒适度评价方法为基于预测平均投票数(Predicted Mean Vote，PMV)指标的方法.该方法下，影响人体热舒适度的因素主要包含空气参数及人体参数，其中空气参数包含空气温、湿度、气体流速；人体参数包含衣着热阻及新陈代谢率.但PMV方法必须进行大量的数据建立及调查研究，因此电采暖设备难以实现针对人体舒适度的实时响应，因此，本文采用简化的人体热舒适度模型，以可快速量测的室内温度、湿度为基本变量，建立简化的人体热舒适度评价指标[9].

PMV=m(Tid-Tod)+nPv-c，

(4)

公式中：m、n、c为统计参数；Pv为空气湿度.其计算方法为采用传统热舒适度模型进行PMV7阶尺度评价并建立相应评价指标，进一步以房间内空气温湿度为变量，采用双线性回归方法，拟合计算m、n、c数值.

结合长春某小区室内相关参数及标准[10]计算得到标准PMV指标如表1所示：

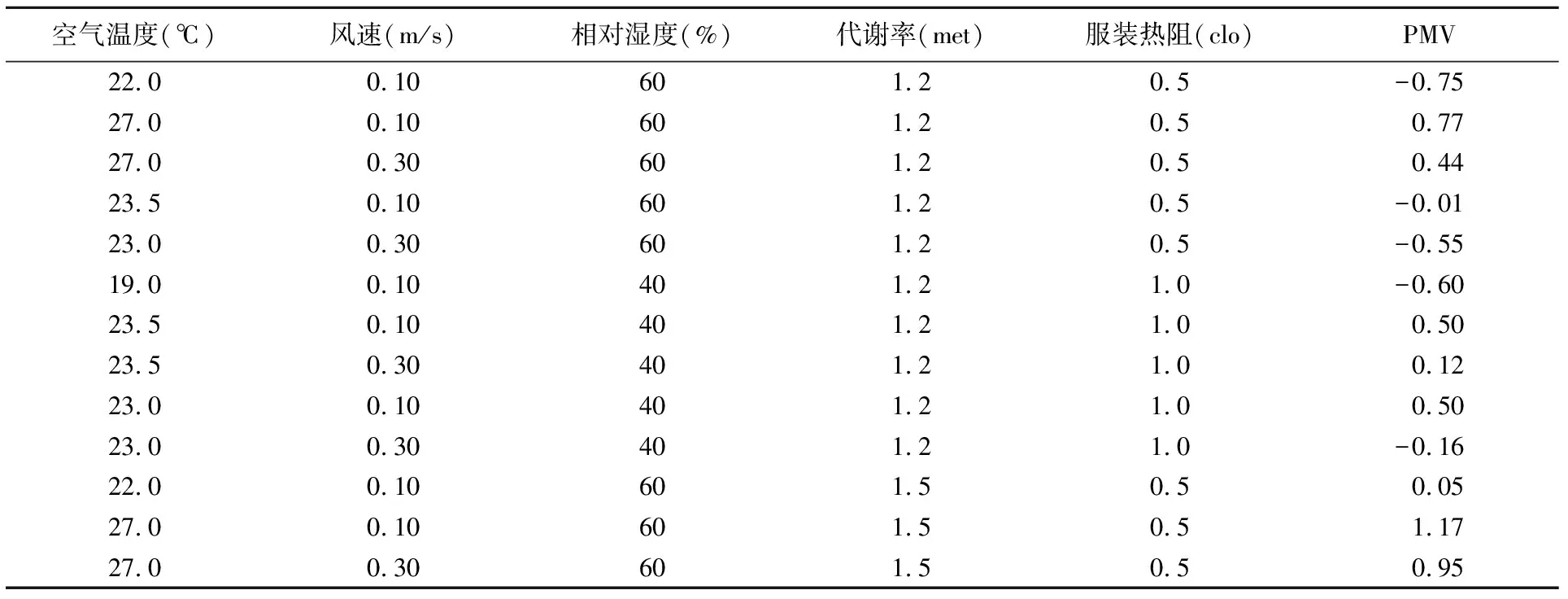
表1 PMV计算结果

在此基础上，建立温湿度计PMV的二元线性回归方程为

PMV=0.18×Ta+0.03×Pv-4.04.

(5)

由于PMV指数为定性指标，在进行计算时需将其转化为可定量表征热舒适度的指标，本文选取预计不满意率(Predicted percentage dissatisfied，PPD)为量化参数，以表征人体热舒适度，其中，PMV确定后，可通过下式计算PPD.

PPD=100-95×e(-0.033 53×PMV4-0.217 9×PMV2).

(6)

由公式(6)可以看出，当PPD指标最小时，可以获得最优舒适度.

2.2 经济性目标

恒定温度上下限的分布式电采暖设备在运行过程中难以响应电价变化，因此需针对取暖期间所执行的居民峰谷分时电价，制定以电费表征的经济型目标.以吉林省为例，峰、谷时分别对应8：00-21：00、21：00-次日8：00，电价分别为0.562、0.329元，在此基础上建立以用户采暖费用最低的经济性目标

(7)

公式中：J为用户电价；t为用户用电时间；Pt为用电时间所用功率；Ct为用户用电时段电价.

2.3 约束条件

(1)分布式电采暖设备电-热特性数学模型为

Php.t=Qhp.t/COPt，

COPt=f(Qhp.t/Qhp_rate)，

(8)

公式中：COPt为对应时段分布式电采暖设备能耗比，可根据具体设备进行确定；Qhp.t、Qhp_rate分别为分布式电采暖设备额定功率及额定制热功率.

(2)电采暖设备开启时的运行功率约束为

0.5Php_rate≤Php.t≤Php_rate，

(9)

公式中：Php_rate为分布式电采暖设备额定输出电功率.

(3)舒适度指标约束：

考虑到相关规范要求，设置舒适度指标约束为

5%≤PPD≤95%.

(10)

3 分布式电采暖设备变温范围控制策略

3.1 MOPSO多目标优化算法

多目标优化问题为在设定的多目标下的求解问题，一般而言，多目标优化问题包含n个决策变量及m个目标函数为

min/maxy=f(x)=(f1(x)，f1(x)，…，fm(x))，

s.t.gk(x)≤0，k=1，2，…，P，

hh(x)=0，j=1，2，…，Q，

(11)

公式中：x=(x1，x2，…xn)为n个决策变量；y=(y1，y2，…ym)为m个目标向量；gk(x)、hk(x)分别为需要满足的P、Q个不等式约束及等式约束.

针对多目标优化问题传统的求解思路主要有两种，一个是多目标经过加权变成单目标问题(可以采用PSO算法)但是这种方法对于权重的处理问题难以得到解决，另外一种方法是以MOPSO及遗传算法为代表的多目标优化方法，该方法不用考虑加权问题，可以实现更好的多目标优化问题.

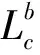
(12)

公式中：1≤j≤d，1≤c≤A.

当第b次迭代结束后，其对应的个体最优位置pbest与全局最优位置gbest分别为

(13)

公式中：第c个粒子迭代计算过程中速度及位置的更新过程可通过公式(14)、公式(15)进行计算.

(14)

(15)

公式中：r1、r2为加速因子，其决定粒子群算法中种群经验和个体经验对粒子运动的影响；w为惯性权值，表征个体在更新速度时对原有速度的保持程度.MOPSO算法基本流程如图2所示.

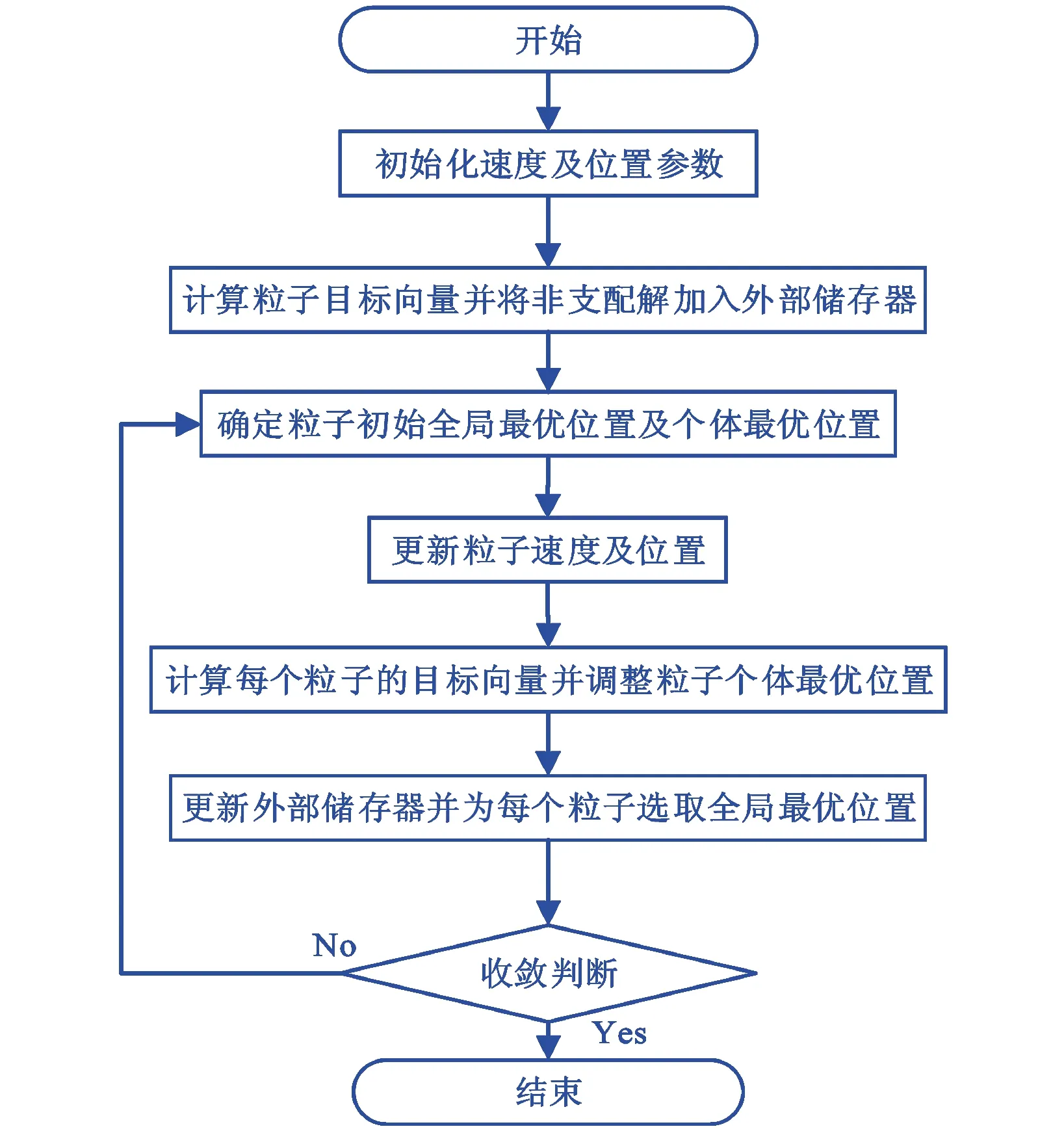
图2 MOPSO流程图

由于MOPSO方法求解结果为多目标条件下的非劣解集，因此需要针对非劣解集进行多目标决策分析以获得最终解.本文综合考虑[11]舒适度及经济性的情况，采用加权多目标综合满意度决策方法，其中，舒适度及经济性的综合满意度权重分别为0.7、0.3，定义综合满意度为[11]

S=0.3u1+0.7u2，

(16)

公式中：S为综合满意度；u1、u2分别为经济性及舒适度满意度指标，采用模糊隶属度方法计算，即

(17)

公式中：fmax及fmin分别为非劣解集中所对应目标函数的最大值及最小值.

3.2 分布式电采暖设备变温控范围方法

(1)采集房间结构参数，热力学参数，并在历史数据基础上得到简化PMV指标相关系数.

(2)根据实时采集数据，采用MOPSO方法求解非劣解，在非劣解的基础上采用加权多目标综合满意度决策方法，求解最优解，获得最优温度及时段电费.

(3)根据最优温度及时段电费控制分布式电采暖设备的启停时间及输入功率，实现分布式电采暖设备温控范围实时变化.

4 算例分析

4.1 仿真参数

本文针对长春某小区相关参数进行采集，在此基础上进行仿真分析，考虑到分布式电采暖设备在实际运行过程中受房屋情况影响，因此本文根据房屋不同类型，将房间分为I～V类，结合房屋类型及温控方式，对分布式电采暖设备运行效果进行分析，其中房间结构示意图如图3所示，房间热力学参数及房屋结构参数如表2、表3所示.

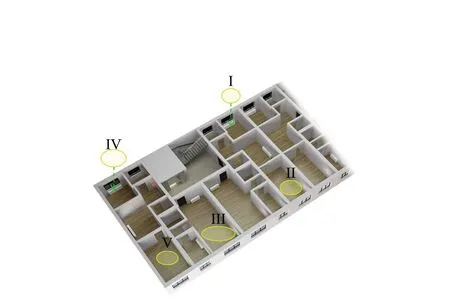
图3 房屋结构示意图

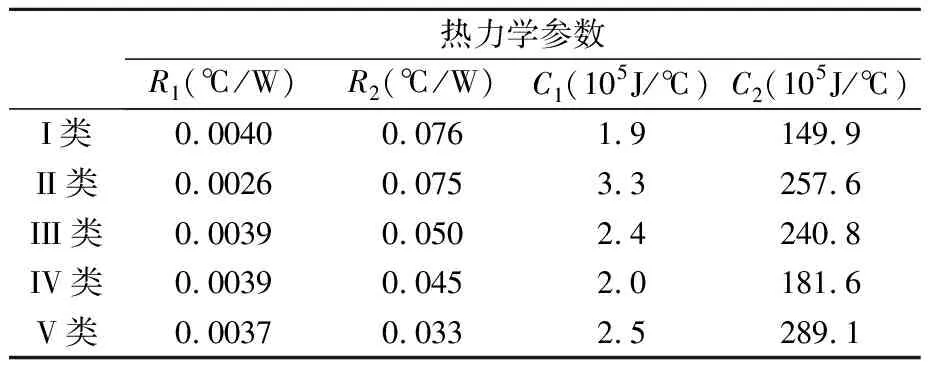
表2 房屋热力学参数

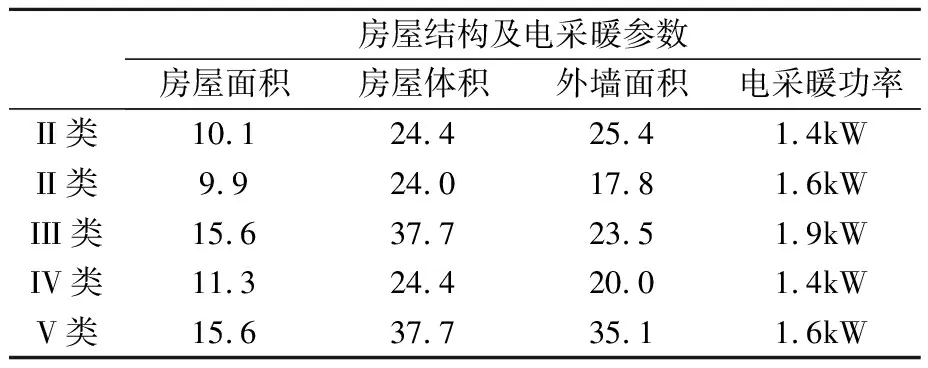
表3 房屋结构参数

结合表2、表3及图3可以看出，不同类型房间热力学参数受到房屋结构的影响存在一定差异，在传统的恒温范围情况下，热力学参数的差异性将会影响分布式电采暖设备使用情况及人体舒适度.

4.2 恒温范围温度采集结果

进一步，通过房屋内外所设置的温度采集装置，监测室内外温度变化情况，III类房间室内外温度变化情况如图4所示.

由图4(a)可知，当天室外最高温度为-6.3 ℃，出现在14：49，最低温度为-20.3 ℃，出现在7：09，室外温度随着时间变化较为明显，呈现中午温度较高、夜晚温度较低的变化情况.

图4(b)所示为分布式电采暖设备传统恒定温度上下限控制方法，温度上、下限分别为25 ℃、19 ℃.不难看出，恒温限模式下分布式电采暖设备开启时，设备输入功率不随时间变化，对电价无响应，经济性较差；恒温限模式下分布式电采暖设备无法针对室外环境变化做出相应调整，人体热舒适度在该模式下较差.

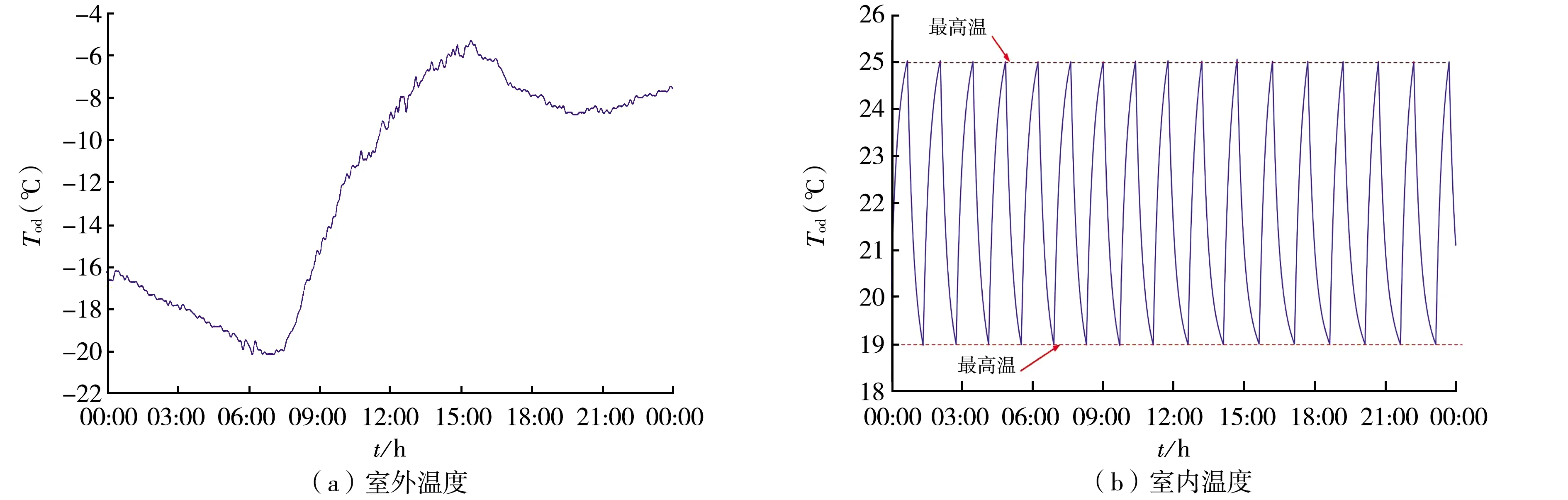
图4 III类房间室内外温度变化

4.3 变温范围仿真结果

采用MOPSO算法，以经济性及舒适度为目标，进行仿真计算，并进行最优解的选取，分别以PPD及相应时刻电费(用电量与对应时刻电价乘积)为横、纵坐标，不同房间不同时段结果如图5所示.

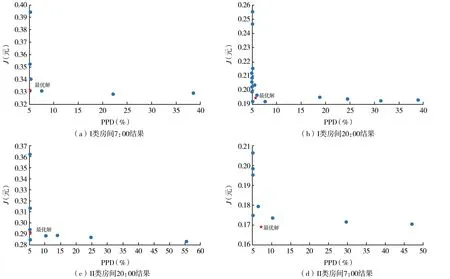
图5 MOPSO算法仿真结果

由图5可知，粒子群算法能够较好的计算出不同房间不同时段多目标条件下的非劣解，并在采用加权多目标综合满意度决策方法后，可求得最优解.结合图5可以看出，不同房间不同时段用户分布式电采暖设备所需电费不同，即在考虑舒适度最优的情况下，分布式电采暖设备运行状态(启停时间、运行功率)不同.在MOPSO算法求解并确定最优解的同时，进行分布式电采暖设备变温范围分析结果如图6所示.

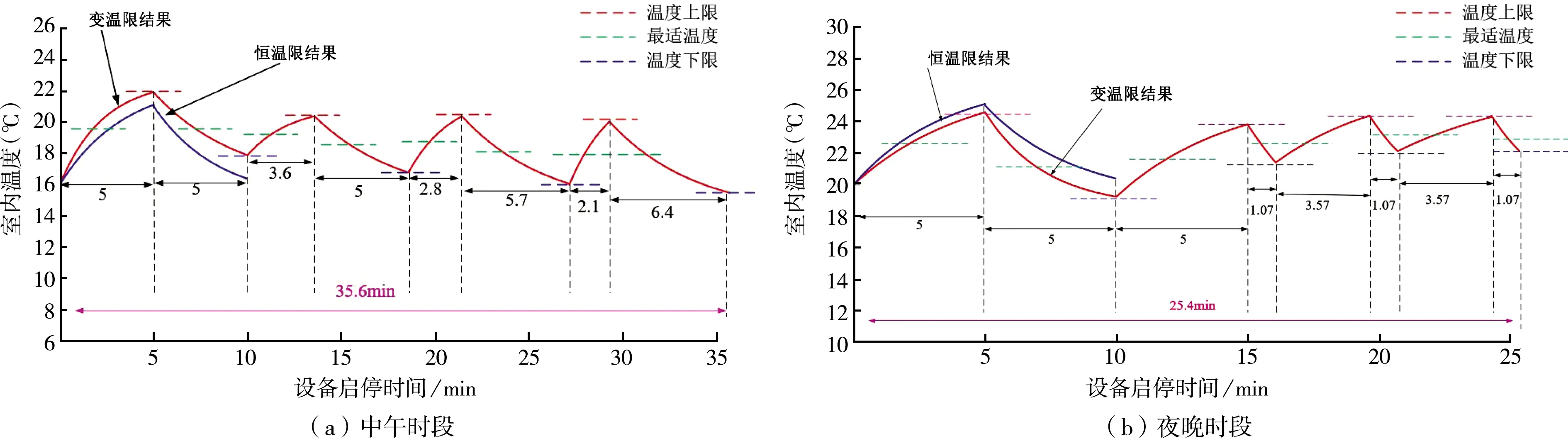
图6 分布式电采暖设备变温限结果

图6所示仿真结果均从设备第一次开启进行分析，忽略分布式电采暖设备温度累积影响[12]，结合图6(a)可以看出中午时段设备开启0 min～5 min内变温限模型相较于恒温限模型升温速度较快且温度上限较高，这是由于设备初次开启时变温限方法及恒温限方法初始温度及输入功率一致，但变温限方法受到室外温度的影响，致使其升温速度较快且温度上限略高于恒温限方法.

5 min～8.6 min时段，变温限方法下设备升温速度变缓且设备开启时间缩短，温度上限相比于设备初次开启降低.分析其主要原因，中午时段人体最适温度受到室外温度影响从而降低，变温限方法考虑最适温度及分时电价影响，降低输入功率，缩短设备开启时间，从而可提高人体热舒适度及经济性.

8.6 min～13.6 min时段，设备关闭，自然降温，在设备下一阶段的启停过程中，设备开启时间进一步缩短，关闭时间延长，分析其主要原因，中午时段屋内热量散失较慢，因此，人体最适温度相比于设备初次开启时逐步降低，从而使得设备开启时间逐步缩短，输入功率下降，设备温度上限缓慢降低.

结合图6(a)、图6(b)可以看出，相同启停次数(4次)下，变温限方法中午、夜间时段启停总耗时分别为35.6 min、25.4 min，相较于中午时段，夜间时段设备单次启停时间更短.与此同时，夜间时段分布式电采暖设备开启后室温升高速度变缓，设备关闭后室温下降速度变快，温度上下限逐步升高，分析其主要原因，夜间室内外温差较大，人体最适温度相较于中午时段有所增加，且由于降温速度加快，热量散失增加，为了维持人体最适温度，设备单次启停时间缩短.

4.4 优化效果分析

对不同类型房间恒温限方法及变温限方法下人体舒适度、经济性指标仿真结果进行分析，并采用线性插值方法拟合各指标，其中房间类型如表2所示，仿真结果如图7所示.

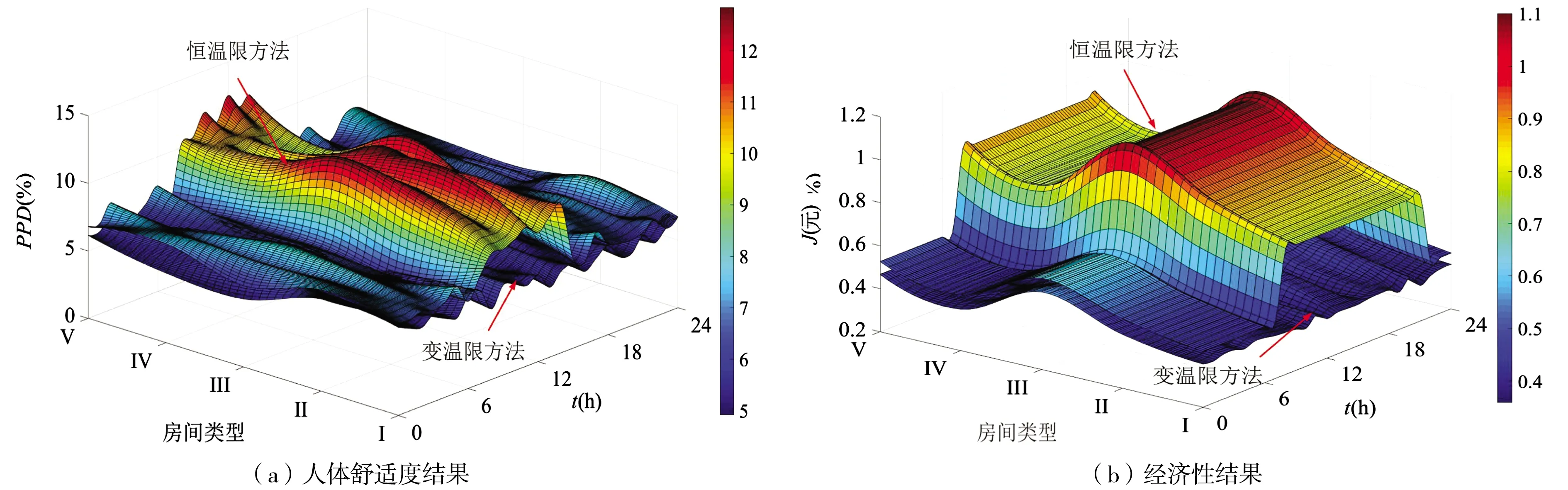
图7 不同温度上、下限制定方法仿真结果

由图7(a)可以看出恒温限方法PPD明显高于变温限方法，且恒温限方法中午时段PPD较高，其中中午时段II、III、V类房间PPD明显高于I、IV类房间.结合图4、图7分析其主要原因，恒温限方法在中午时段难以对室外温度变化做出反应，因此中午时段采用恒温限方法人体舒适度较差，并且II、III、V类房间朝阳，因此中午时段温升明显，致使II、III、V类房间PPD指标高于I、IV类房间.由图7(b)可以看出，变温限方法在8～21时各时段电费明显低于恒温限方法.分析其主要原因，变温限方法考虑分时电价影响，在室外温度较高时段降低设备输入功率，缩短设备开启时间，从而减少分布式电采暖设备用电费用，提高设备经济性.

在此基础上，结合综合满意度指标S，以两小时为一分析时段，计算综合满意度指标S均值，对恒温限及变温限方法综合满意度结果进行分析，如表4所示.

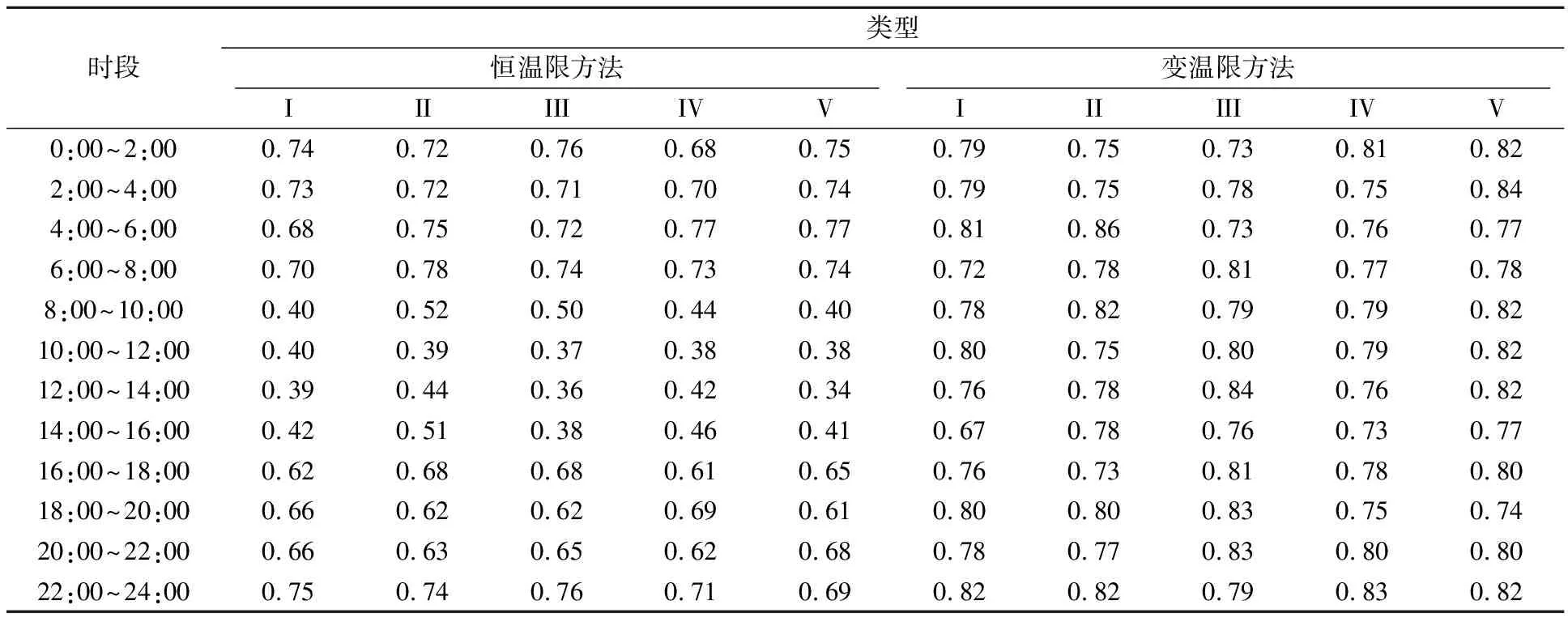
表4 综合满意度结果

由表4可以看出，不同时段、不同类型房屋综合满意度不同，其中采用恒温限方法时0：00～8：00、16：00～24：00时段下的综合满意度相比于8：00～16：00时段较高，而采用变温限方法时一天内综合满意度变化较小，对比恒温限方法及变温限方法可以明显看出8：00～16：00时段变温限方法综合满意度明显高于恒温限方法.分析其主要原因，综合满意度为考虑经济性及舒适度的线性加权结果，变温限方法经济型及舒适度指标在8：00～16：00时段明显高于恒温限方法，因此其综合满意度也较高.

综合图6、7及表4可以看出，分布式电采暖设备采用变温限方法后能够对分时电价及室外温度变化做出响应，使得设备开启时间、输入功率、温度上下限做出相应调整，能够更好的满足人体热舒适度及经济性的要求.

5 结 论

本文针对分布式电采暖设备温度上下限设定方法问题，综合考虑分布式电采暖设备经济性及人体舒适度目标，建立基于多目标优化的分布式电采暖设备变温限方法，采用MOPSO算法求解多目标模型，结合实测数据进行仿真分析，对比传统恒温限方法，结果表明：基于MOPSO的分布式电采暖温度范围多目标优化方法可以实时响应室外温度及分时电价，通过改变设备输入功率、启停时间达到改变设备温度上下限的目的，满足人体舒适度及经济性要求，为分布式电采暖设备温度上下限制定提供新的思路.