基于MADDPG算法的家用电动汽车集群充放电行为在线优化
2021-11-01戴武昌刘艾冬马鸿君
戴武昌,刘艾冬,申 鑫,马鸿君,张 虹
(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012;2.国网辽宁省电力有限公司抚顺供电公司,辽宁 抚顺 113000)
近年来,电动汽车因为具有清洁环保、噪音低等优势,在全球范围内得到大力发展[1-3].在需求响应环节中,电动汽车具有可中断负荷的用电特性,为其充电行为优化提供了可能[4].若有效利用,电动汽车也可以为电网提供诸如削峰填谷等作用[5-6].如何兼顾用户侧经济性和网侧转移限制峰值负荷的要求优化充放电行为成为重要的研究课题.
目前,有许多的优化模型和算法应用于电动汽车充放电行为调度中,以满足电网侧或用户侧的利益.文献[7]提出了基于蒙特卡洛和粒子群算法的电动汽车有序充放电控制策略,运营商考虑多种因素制定策略,目的是限制电网功率和降低用户成本.文献[8]提出了一种基于超图模型的最小能量损耗路由算法,通过电动汽车异地充放电进行电能的运输,并规划输送路径以减少了输送过程的能量损失.文献[9]建立了需求响应下代理商定价与购电策略,通过主从博弈的方式实现代理商与车主双方利益最大化.文献[10]建立了一种分时电价下电网与用户双方互动的主从博弈模型,以极小化负荷均方差和车主成本为优化目标,实现了良好的经济效益与调峰效果.文献[11]引入电动汽车集群管理机构,建立以最小化网侧生产成本和用户侧充放电成本为目标的主动配电网供需协同优化调度模型,得到的优化调度策略不仅降低了生产成本和车主用电费用,而且改善了系统的电压质量.
上述文献提供了电动汽车充电行为优化调度的解决方案,但没有充分挖掘历史用电数据特性以指导电动汽车充放电行为.
近年来,由于具备对大数据的分析处理能力以及精准快速的决策能力,深度强化学习成为研究热点,并广泛应用在电动汽车充放电调度中.文献[12]应用了DDQN算法进行汽车充电策略的制定,并通过调整电网节点的电动汽车负荷,保证了配电网满足电压约束.文献[13]将家用电动汽车归类为家用负荷中的可中断负荷,将A3C算法与基于设备运行状态概率分布的住宅用电模型相结合,生成的能耗调度策略可用于向电力用户提供实时反馈,以实现用户用电经济性目标.文献[14]提出了一种基于Q-learning的V2G电力交易决策算法用于降低用电成本.
上述文献提供了电动汽车充放电行为策略的优化方案,但控制策略都是离散化的,缺少灵活性,且少有考虑通过集群内部合作的方式转移和限制峰值负荷的充放电行为优化.
多智能体深度确定性策略梯度(Multi-Agent Deep Deterministic Policy Gradient,MADDPG)算法是一种融合博弈与数据处理的算法,由于其在多智能体环境中具备良好的决策能力,成为了多智能体深度强化学习的重要算法之一[15].
本文首先基于用户的历史用电数据,根据电动汽车用户群体与网侧双方的需求建立了家用电动汽车集群充放电行为优化调度模型,鼓励用户参与需求响应;其次,通过深度神经网络对大规模复杂数据的特征提取与存储,并利用强化学习算法在控制与决策方面的优势,实现对家用电动汽车充放电调度的在线优化.最后,算例分析表明该算法可以兼顾用户的经济性和舒适性,同时可以转移网侧峰值负荷,并限制峰值负荷的大小.
1 家用电动汽车充放电行为调度模型
1.1 家用电动汽车用电场景分析
本文的用电场景是一处智能小区,在该小区内,存在多户拥有电动汽车的家庭,住宅中均装有充电装置供各自的电动汽车使用.用户侧通过高级量测体系与电网侧进行双向实时通信,在线交换电价信息和用户的电动汽车充放电情况,并通过用户调度中心参与电力调度.示意图如图1所示.
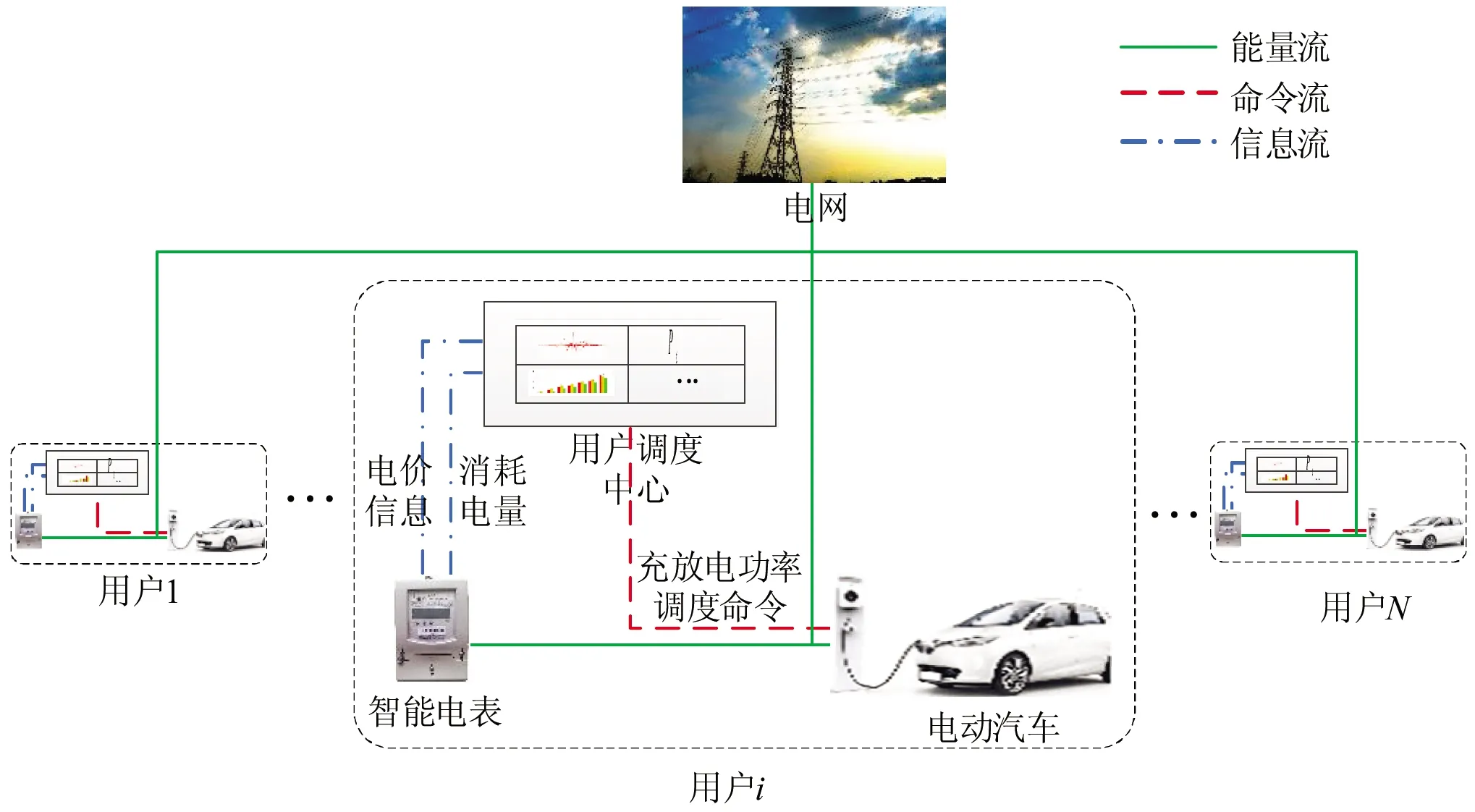
图1 家用电动汽车充放电管理系统
电动汽车用户可以自行决定出行时间与行驶里程,仅在电动汽车处于在家状态下才被允许参与调度.用户除了可以通过供电公司购电为电动汽车供电外,还可以将电动汽车作为家用储能装置向电网出售电能获取收益.
1.2 不确定电价信息下充放电行为分析
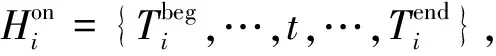
电动汽车参与充放电行为优化调度的主要目标是实现电动汽车充放电成本的最小化,同时兼顾用户的舒适性和电网对电动汽车负荷的限制,因此需要尽可能提高用户的综合收益,即综合成本的最小化.用户的综合成本可以表示为
(1)
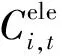
(2)
公式中:λt为时段t的电价信息;li,t为电动汽车i在时段t的充放电量,表示为
(3)
公式中:pi,t为电动汽车i在时段t的充放电功率;pi,t∈[-pmax,pmax],当电动汽车充电时pi,t为正值,放电时pi,t为负值.
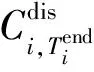
(4)
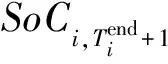
SoCmin≤SoCi,t≤SoCmax,
(5)
公式中:SoCmin为荷电状态的最小值约束.
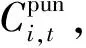
(6)
公式中:ρ为惩罚系数,ρ>0;lt为电动汽车集群在时段t的总用电负荷,可以表示为
lt=∑i∈Bli,t;
(7)
lth为产生惩罚成本的充电功率阈值,可以表示为
lth=kthNpmax;
(8)
公式中:kth为充电阈值百分比,表示电动汽车集群充电功率阈值占集群最大充电功率的百分比;pmax为电动汽车最大充放电功率.
1.3 电动汽车集群的强化学习设置
由于电动汽车集群的充放电过程具备马尔可夫性,也包含用户之间的合作,该过程可以描述为马尔可夫博弈,这是多智能体强化学习算法的基础.在多智能体环境中,由于智能体之间存在着联系,每个智能体的下一状态不仅与当前自身的状态与动作相关,还与其它智能体的状态与动作相关.每个智能体不能完全观测其他智能体的状态和动作,需要根据自身的观测结果从复杂的状态空间中选取对自己更加有利的动作,保证每次决策的优势不断累积,形成优势策略[16].
在电动汽车的充放电模型中,每个智能体代表一辆电动汽车,代替用户进行充放电操作与参与环境的交互.电动汽车i在时段t充放电功率pi,t可以作为智能体i的动作ai,即
ai=pi,t.
(9)
将每一时刻的电价信息、电动汽车的充放电操作权限和荷电状态设置为状态量.智能体i能够观测到的状态量oi设置为
oi={λt,σi,t,SoCi,t},
(10)
公式中:σi,t为电动汽车i在时段t的充放电操作权限,表示电动汽车是否允许接入电网进行充放电操作,可以表示为
(11)
全局状态量x包含当前时刻所有智能体的观测量,即当前电价和电动汽车集群的状态信息,定义为
x={o1,…,oN}={λt,σ1,t,SoC1,t,…,σN,t,SoCN,t}.
(12)
在执行动作a={a1,…,aN}后,所有智能体由状态x转移至下一状态x′,并从环境中获取各自的奖励值ri和下一时段各自的观测量o′i.奖励值ri反映每个智能体采取动作的优劣.根据公式(1)的优化目标,智能体i获得的奖励值ri定义为
(13)
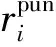
(14)
2 多智能体深度确定性策略梯度算法
MADDPG算法源起于确定性行为策略算法(Deep Deterministic Policy Gradient,DDPG),能够在动作空间是连续的情况下,无需对动作空间进行离散化,直接输出一个确定的动作值,从而避免由动作空间离散化而带来的复杂运算[17-18].
2.1 算法描述
在环境中含有N个智能体,每个智能体仅能观测到环境的局部状态信息,无法得知全局状态,且含有神经网络,网络参数分别为θ={θ1,…,θN}.MADDPG算法的神经网络结构如图2所示.MADDPG中每个智能体的主网络包含两种的网络:一是策略网络μ,用来做出符合当前环境和状态的决策;二是价值网络Q,用来评判策略网络输出动作的优劣.
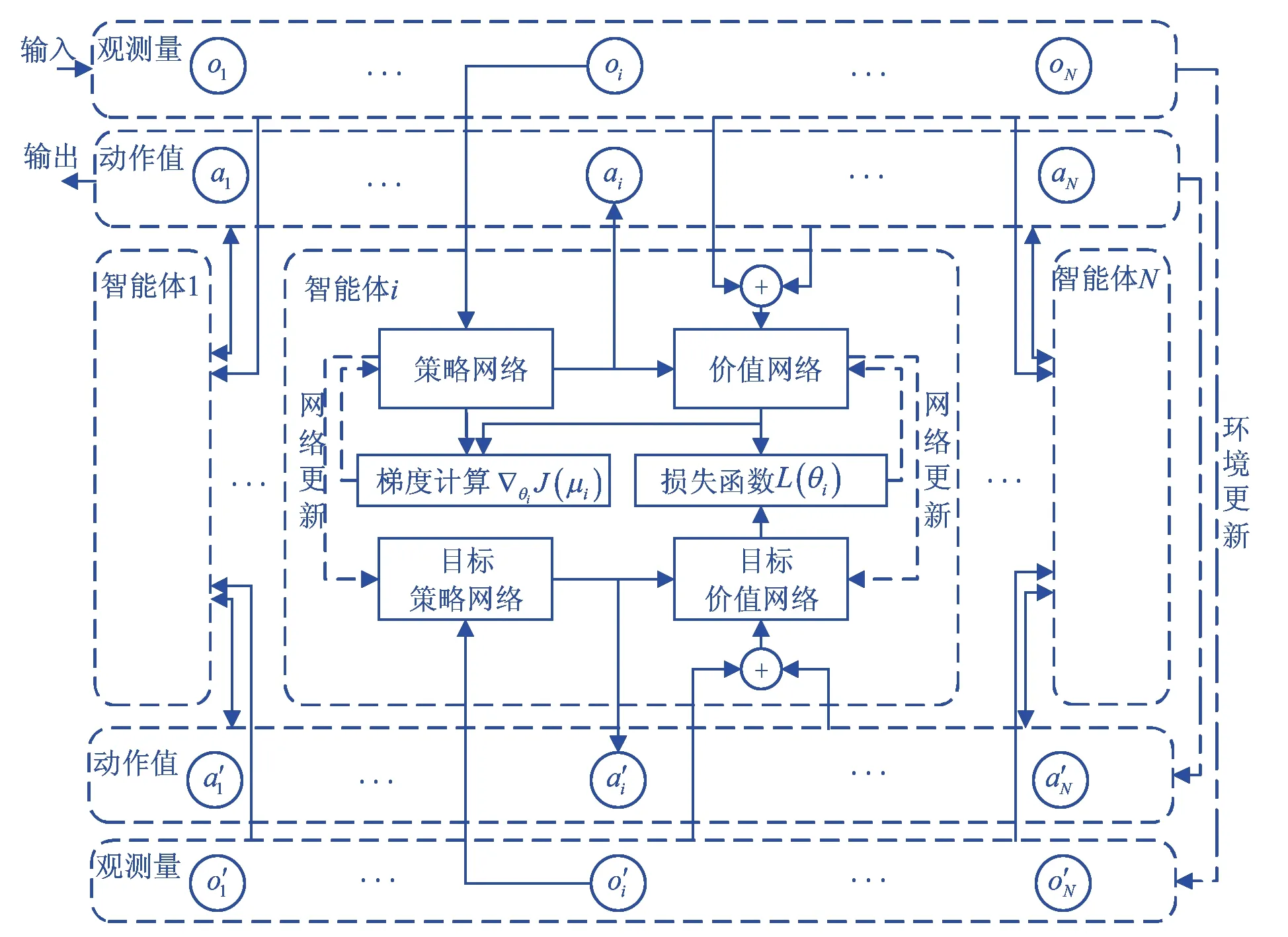
图2 MADDPG算法神经网络结构示意图
策略网络引入确定性策略替代随机性策略,网络输出从动作的概率分布变为具体的动作,有助于算法在连续动作空间中进行学习.引入白噪声机制,用于提高策略网络在特定环境状态下输出不同的动作值的可能性,提高训练的探索度.智能体i的动作值ai为
ai=μi(oi)+Nt,
(15)
公式中:μi为智能体i策略网络输出的策略;Nt为白噪声.
每次策略网络根据oi生成动作ai后,环境会返回奖励值ri与下一时刻的观测量o′i.将所有智能体的信息{x,a1,…,aN,r1,…,rN,x′}存入经验池D中,等待训练阶段作为训练样本供神经网络使用.
MADDPG算法引入DDPG的目标网络结构,与主网络的结构相似,目的是保证训练的稳定性.目标网络同样分为目标策略网络μ′和目标价值网络Q′,分别使用主网络中的策略网络参数和价值网络参数进行初始化,作用是替代主网络完成在下一时刻的决策与评判,并将做策略网络与价值网络的更新.
关于预期回报J(μi)的策略网络更新公式为
(16)
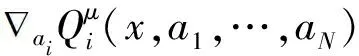
价值网络通过最小化TD误差来更新网络参数[19],更新公式为
(17)
公式中:L(θi)为价值网络的损失函数,用于评估价值网络估计的价值函数与实际价值函数的误差;y为实际的动作值函数,可以表示为
(18)
主网络的训练目标是最大化策略网络的期望收益J(μi),同时最小化价值网络损失函数L(θi).对主网络中的策略网络和价值网络以学习率α为更新步长进行更新,更新公式分别为
θi←θi+α∇θiJ(μi),
(19)
θi←θi-α∇θiL(θi).
(20)
目标网络采用Soft update的更新方式,主网络参数用于目标网络的更新,目标网络的更新幅度由目标网络更新率τ决定,0≤τ<1,更新公式为
θ′i←τθi+(1-τ)θ′i.
(21)
2.2 充放电行为实时优化流程
基于MADDPG算法的电动汽车充放电实时优化流程如图3所示.MADDPG算法的学习过程包括训练阶段与执行阶段,采用集中式训练、分布式执行的学习框架.
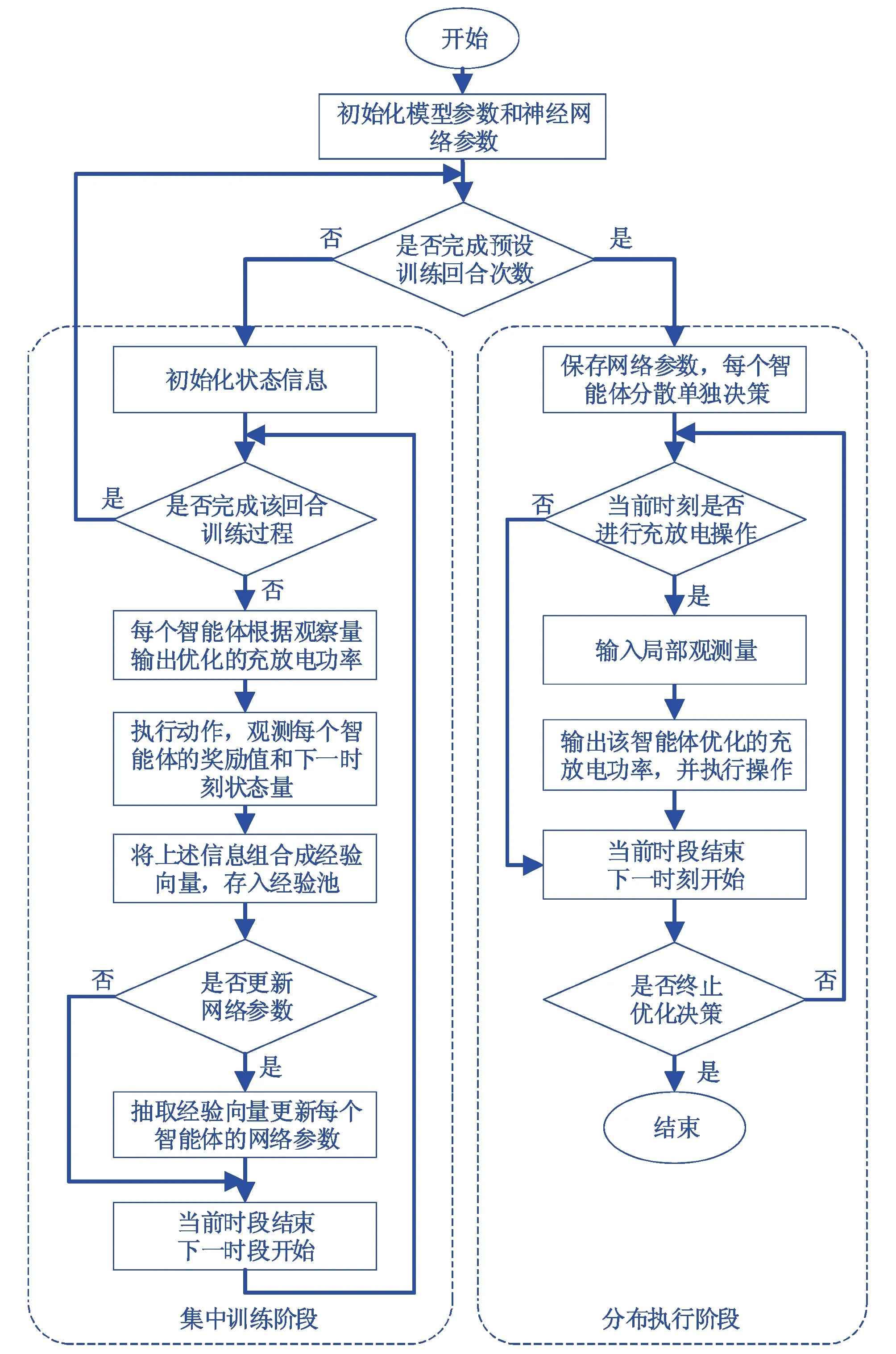
图3 充放电行为优化流程图
在训练阶段,系统首先依据电价信息、电动汽车集群的操作权限和荷电状态的历史数据进行行为探索,学习现实环境中多种可能发生的用电情况.然后,依据奖励函数评估每个充放电行为的优劣.如果该行为为集群带来更多收益,则给予该充放电行为较高的奖励值.反之,给予该行为较低的奖励值.将这些信息作为训练素材存储在经验池中,并通过抽样的方式参与神经网络的集中训练,积累大量的先验知识.
在执行阶段,每个智能体不需要调动各自的价值网络对当前的状态与策略进行评价,依靠训练环节中完成优化的策略网络可以进行充放电行为的输出.向各个智能体的策略网络中输入局部观测量oi={λt,σi,t,SoCi,t},经过策略网络运算输出优化后的充放电动作,实时指导用户的充放电行为,以满足用户侧与电网侧的多种需求.
由于算法采用集中式训练、分布式执行的学习框架,每个智能体在训练阶段考虑到了其他智能体对环境和自身的影响,有利于降低电动汽车用户群体的成本.在执行阶段,每个智能体的神经网络已经经过训练并得到优化.可以将各个智能体分散在用户家中,根据自身的观测量做出优化的行为决策,同时利于保护用户隐私.
3 算例分析
3.1 参数设置
本文采用美国某电力公司2017年~2018年制定的电价数据.其中,2017年电价数据作为训练集使用,2018年数据作为测试集使用.仿真车型相关参数如表1所示.充放电模型参数如表2所示.

表1 电动汽车参数

表2 电动汽车充放电模型参数
由于用户出行行为具有习惯性与规律性,以出行链的方式对用户出行状态进行描述[20].图4表示用户较为常见的出行链,包括以下2个场景:
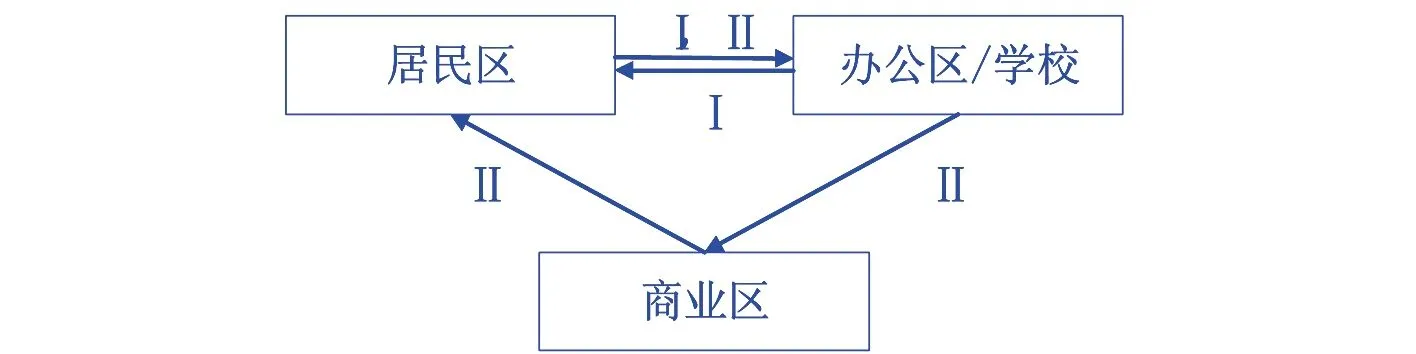
图4 出行链示意图
场景1:居民区→办公区/学校→居民区
生态城市是在人与自然建立关系的基础上产生的一种文化观,这种文化观是在生态学原则上建立起的社会、经济、自然协调发展的新型社会关系,是城市生产力和生产关系发展形成的一种全新的价值体系。生态城市本质上就是一个生态健康的城市,能够有效地将环境资源利用起来,建立健康、适宜人居住的环境,并实现可持续发展的生活方式。
场景2:居民区→办公区/学校→商业区→居民区
根据文献[21],综合场景下集群的电动汽车按照场景1出行的频率占比为65%,按照场景2出行的频率占比为35%.电动汽车的出行时间和到家时刻荷电状态服从正态分布,如表3所示.

表3 出行行为参数设置
算法参数中,折扣因子γ取为0.99,学习率α取为0.001,目标网络更新率τ取为0.01.仿真环境为英特尔core i7-8700@3.2GHz,6核12线程,内存16GB DDR4,软件配置为Python3.7.0,Tensorflow1.13.0.
3.2 结果分析
3.2.1 需求响应能力评估
为了评估智能体参与需求响应的能力,随机抽取某用户在连续120 h内电动汽车用电优化情况如图5所示.在不同的场景下,电动汽车处于在线状态的时段下系统可以做出不同的决策以适应不同的电价水平,最终的荷电状态稳定在较高水平,满足用户用电要求.因为高负荷惩罚项,充电功率被限制,有利于网侧充电负荷的控制.场景1放电行为更多集中在高电价时段,具有更大的调度空间.综合场景的优化效果介于两种场景之间.
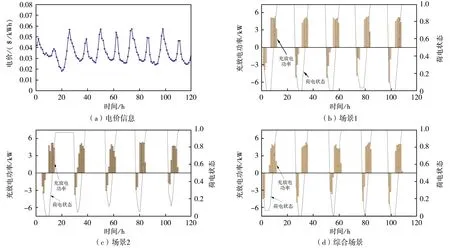
图5 不同用电场景下电动汽车用电行为优化情况
3.2.2 经济性评估
本文对不同场景下用户个体的经济性进行评估.其不同场景下优化前后的用电成本和综合成本如图6(a)、图6(b)所示.考虑到在现实情况中用户无法在每个时段针对变动的电价调整电动汽车的充电行为,对比了优化前的充电模式.在这种情况下,电动汽车到家后以高功率充电,直到电池充满为止,之后不再进行充电,本次充电过程结束.在场景1下,优化后的日平均用电成本为0.262 4$,较优化前降低了0.456 7$.在场景2下,优化后的日平均用电成本为0.480 6$,降低了0.100 4$.在综合场景下,优化后的日平均用电成本为0.350 9$,降低了0.295 8$.由于电动汽车经历了先放电后充电的过程,优化后成本呈先下降后上升的趋势,成本得到控制.
其不同场景下优化前后的费用占比情况如图6(c)所示.在同种场景下,优化后的用电成本普遍低于优化前的用电成本,综合场景的优化效果介于场景1与场景2之间.场景1的用电成本相比场景2优化效果更好,这是由于场景1下用户到家的时间比场景2更早,为系统调度提供了更多的时间,同时场景1下用电过程经历了更多的高电价时段,有利于汽车向电网放电以减小用电成本.同种场景下,综合成本在用电成本的基础上有小幅提高,但优化后的综合成本普遍低于优化前的水平.优化后的潜在成本降低,但潜在成本占比高于优化前,说明该算法在满足用户和电网的潜在需求下,大幅降低了用电成本.
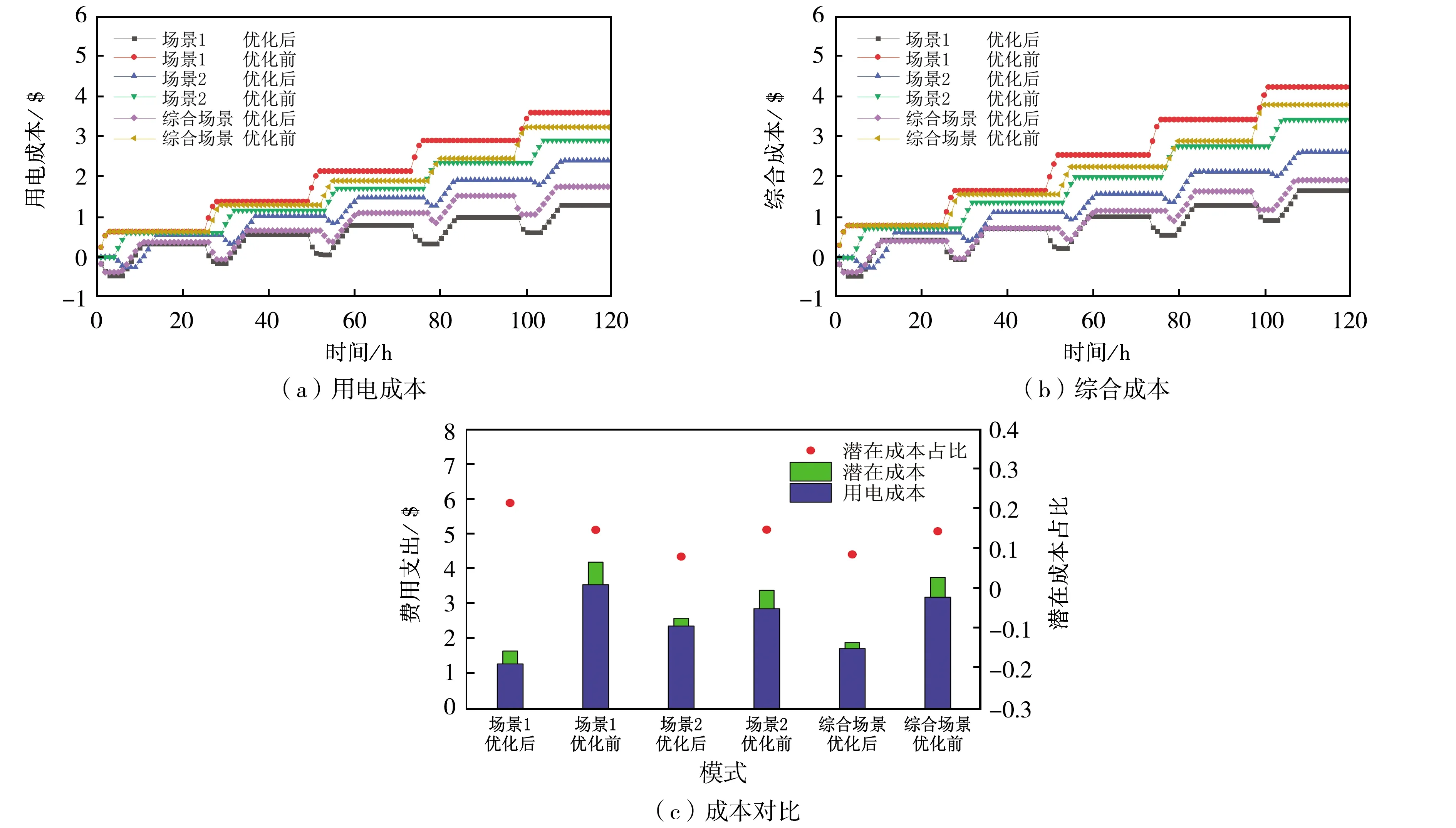
图6 不同场景下的经济性评估
为了验证电动汽车集群的经济性,对含有30辆电动汽车的集群进行分组调度,随机抽取10辆电动汽车,其用户的年费用支出对比如图7所示.用户的优化结果略有差异,这与用户的出行习惯有关.用户的潜在成本占比较低,说明系统能够兼顾用户的出行需要和电网的负荷要求.
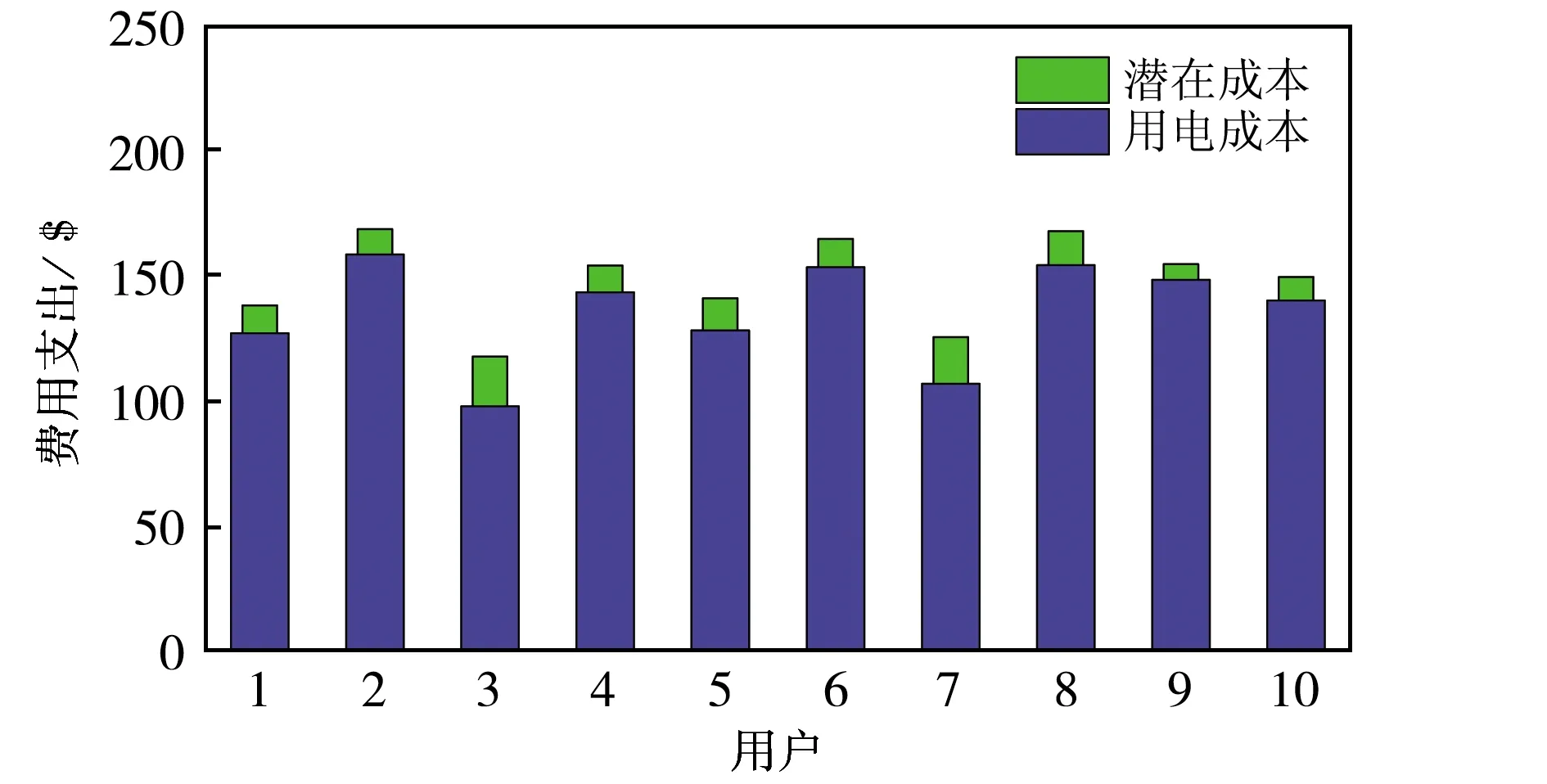
图7 不同用户的年费用支出对比
用户的年平均用电成本如表4所示,在不同场景下优化后的用电成本较优化前有不同程度的下降,说明变动的电价下的充放电决策可以满足用户群体的经济性.
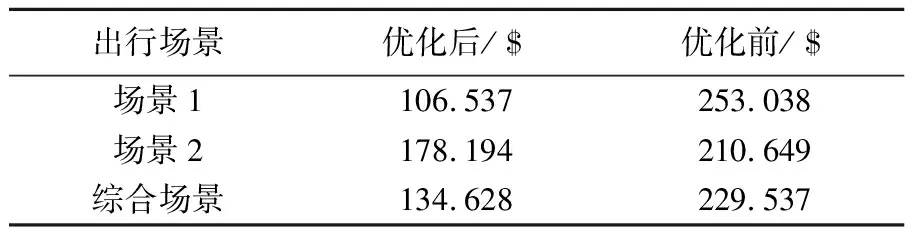
表4 年平均用电成本优化结果对比
3.2.3 负荷情况评估
电动汽车集群每日平均负荷情况如图8所示,其中虚线表示电动汽车集群的充电功率惩罚阈值.原有的充电方式在用电高峰时段进行充电,在17时至次日1时产生两个负荷高峰.经过初步优化后,电动汽车集群整体在17时至23时处于向电网放电的状态,并在次日0时至6时从电网吸收电能,转移峰时负荷,缓解电网压力.引入高负荷惩罚后,峰值充电负荷得到下降,负荷曲线更加平滑,峰值负荷向后续时段转移.这是由于集群的成员在充电行为上产生合作关系,为了防止集群总充电负荷超出阈值对每个用户施加惩罚,智能体对各自的充电功率进行限制,从而降低了峰值负荷.
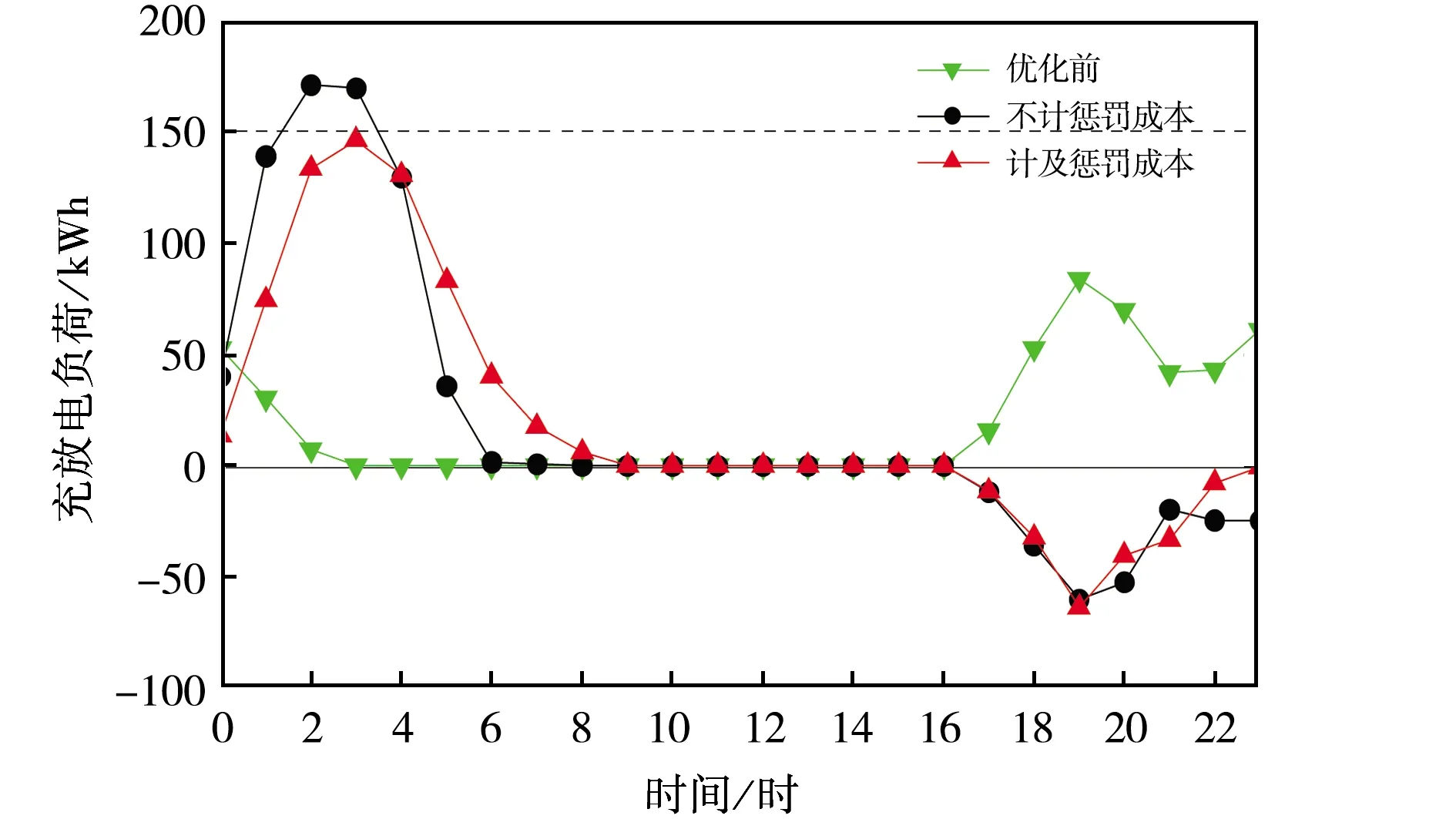
图8 优化前后电动汽车集群充放电负荷对比
3.2.4 舒适性评估
在不同场景下用户的舒适性情况如图9所示.随着不舒适系数的升高,两种场景下的荷电状态在不断升高,直至电池完全充电,但用电成本也随之增加.当相同成本的情况下,场景1的系数比场景2的小,这是因为场景1包含更多高电价时期,系统指导电动汽车放电换取利润,具备更多的调度空间,充电成本较低,此时相对较低的系数可以满足需求;同样场景下,较高的系数使得荷电状态更高,可以带来更好的使用体验.
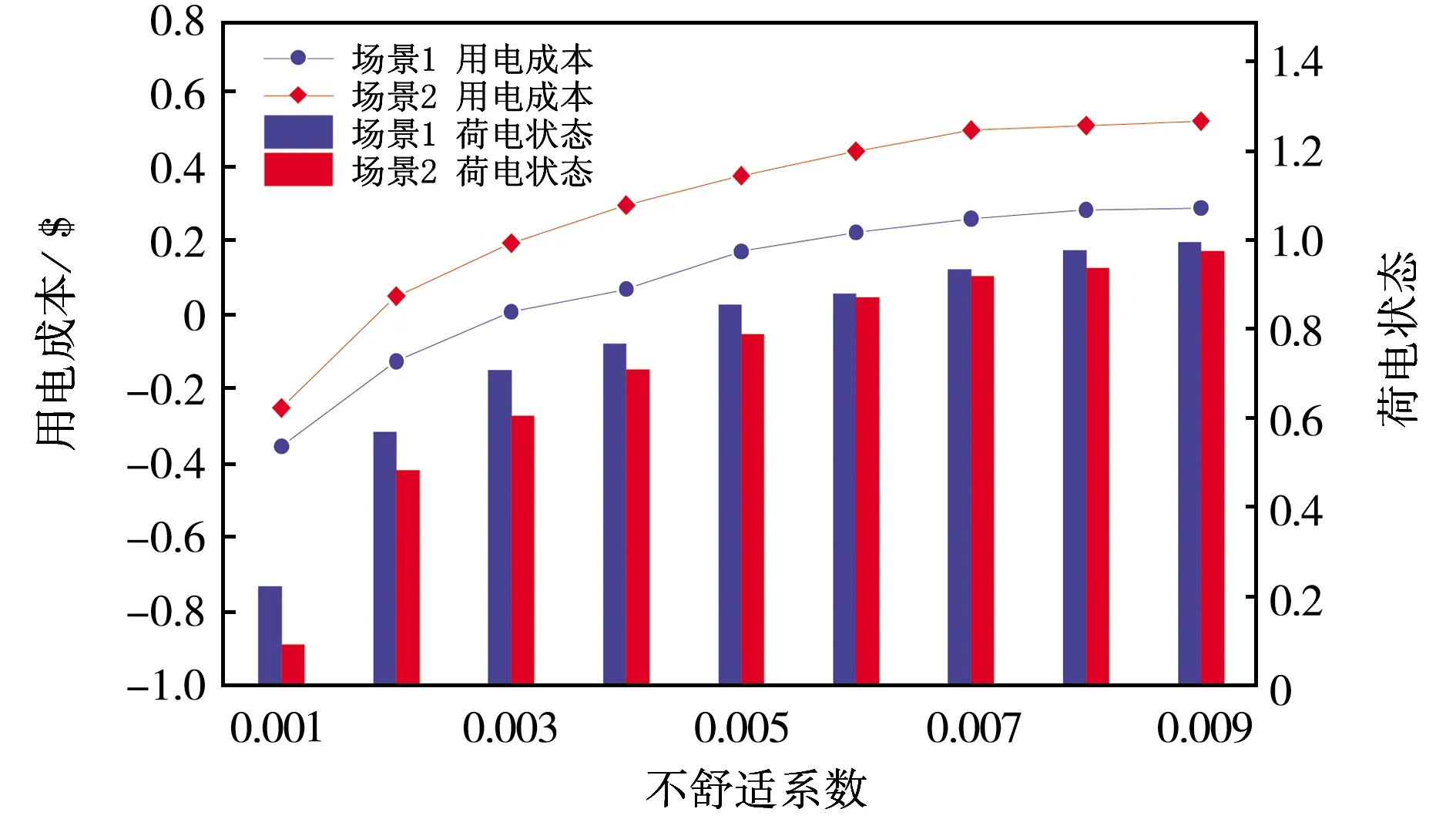
图9 不同场景下的舒适性情况对比
4 结 论
针对电动汽车集群参与需求响应的充放电行为,本文提出了一种基于MADDPG算法的电动汽车集群充放电行为在线优化方法.主要结论如下:
(1)建立了电动汽车集群充放电优化调度模型,综合考虑用户在不同场景下的出行习惯、用能需求及网侧负荷约束,为电动汽车集群参与需求响应提供优化方案.
(2)引入多智能体深度确定性策略梯度算法,采用集中式训练、分布式执行的学习架构,在保护用户隐私的前提下,实现电动汽车集群充放电行为的在线优化.
(3)所提模型可以提高用户用能经济性,在综合场景下的用电成本相比用户原有的充电方式降低约41%,同时可以转移电网峰值负荷,将新负荷高峰限制在最高充电负荷的81%,实现用户群体与电网的双赢.
