局部加密的正弦波纹微通道强化传热的数值研究

2021-11-01张晓蒙马丹丹夏国栋

东北电力大学学报 2021年4期

张晓蒙，马丹丹，夏国栋

(北京工业大学传热强化与过程节能教育部重点实验室，传热与能源利用北京市重点实验室，北京 100124)

随着微电子技术的飞速发展，微电子器件不断向集成度更高、功率更大、速度更快、更加微型化的方向发展.微电子器件的有效散热也受到了巨大的挑战.传统的散热方式已不能满足要求，散热问题已经成为制约微电子技术进一步发展的重要因素.

1981年，Turkerman和Peace等[1]首次提出了“微通道热沉”的概念.与常规通道相比，微通道热沉具有比表面积大、自重轻、体积小等优点被认为是解决高热流密度微型设备散热问题的有效方法.为了提高微通道热沉的散热能力各国学者进行了大量研究.一方面通过增强换热工质的导热系数来强化对流换热效果，如 “纳米流体”它是将一定量的纳米级金属或非金属粒子通过一定的方式添加到水、醇或油等传统液体中，形成均匀、稳定地新型介质[2].研究表明纳米流体可以显著的增强液体工质的传热性能[3-4].另一方面通过改变微通道的结构，增加换热面积、增强流体扰动从而增强对流换热效果.如：水滴型微凹穴微通道[5]、扇形凹穴周期变截面微通道[6-7]、微柱微通道[8].

对于矩形直通道其流线几乎平直于通道壁面，其热边界层通常会沿冷却剂流动的方向增厚.Sui等[9]提出了正弦波纹微通道，发现其压降损失比强化传热小得多.Morteza等[10]以纯水为冷却剂，对三角形、梯形和正弦曲线进行了实验研究，结果显示正弦形微通道具有最好的性能，其次为三角形和梯形.Zhu等[11]对底面波形微通道和侧面波形微通道进行了比较，发现无论波幅和通道长宽比如何，当采用小波长时，上下波状设计比左右波状设计表现出更好的传热性能；然而，在大波长时，两种设计表现出几乎相同的性能.对于微电子器件散热的热匹配的硅基微通道散热器，从加工技术方面考虑，左右波形微通道散热器更容易制作.M.Khoshvaght-Aliabadi等[12]试验研究了不同振幅和波长下的正弦波纹微通道散热器的冷却性能，研究表明较小的波长和较大的振幅更有利于换热但同时伴随着较大的压降.

目前国内外在微通道流动换热研究方面已取得了诸多进展，然而研究结果表明较好的换热效果往往伴随着较大的压降.为此，本文提出了一种局部加密型正弦波纹微通道，在传统波纹微通道的基础上，将通道沿x方向等分为上游、中部、下游三个部分，利用数值模拟的方法探索局部加密位置对正弦波纹微通道换热性能的影响.

1 数值模拟

1.1 几何模型

传统正弦波纹微通道的几何结构示意图如图1所示.

图1 几何结构示意图

考虑到整个硅基微通道热沉的周期性，数值模拟中选取最小的对称单元进行计算.如图1(b)所示，计算区域中间位置为充满液体工质的微通道，两侧为肋壁面.所有微通道计算区域长Lx=12 mm，宽Ly=6.3m m，高Lz=0.4 mm.每根微通道的长度均为12 mm，通道宽度Wc=0.18 mm，通道间的肋壁宽度Wr=0.12 mm.由于通道关于轴线对称，所以数值计算中选取通道侧壁的一半Wr/2作为计算对象.通道高度Hc=0.2 mm，基地厚度δ=0.2 mm.

对传统正弦波纹微通道进行局部加密研究其对单相流动和传热的影响，并与矩形直通道(case0)和传统波纹微通道(case1)进行对比.本文提出的新型波纹微通道是对传统波纹微通道分别对其沿x方向的上游、中部和下游通道进行加密，如图2所示，其上游、中部和下游分别对应波长为λ1、λ2、λ3.相应的具体结构参数如表1所示.

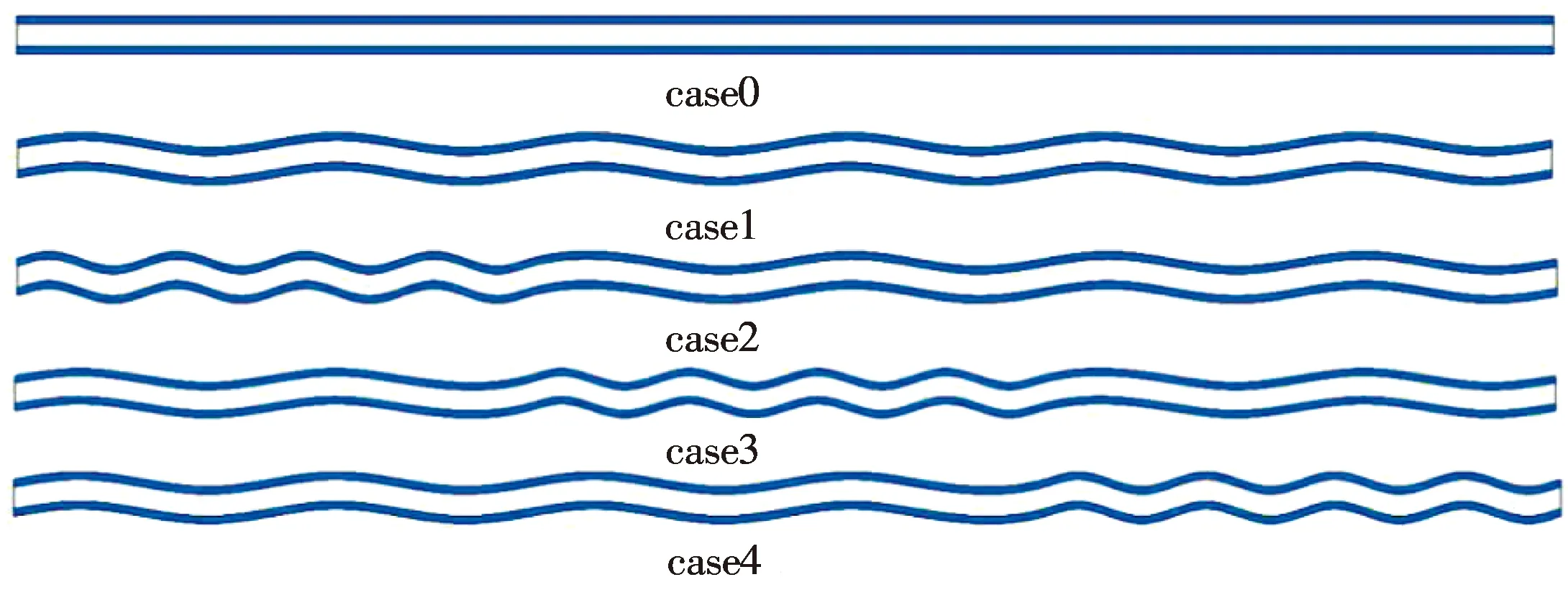
图2 五种微通道结构示意图

表1 微通道的尺寸

1.2 数学模型

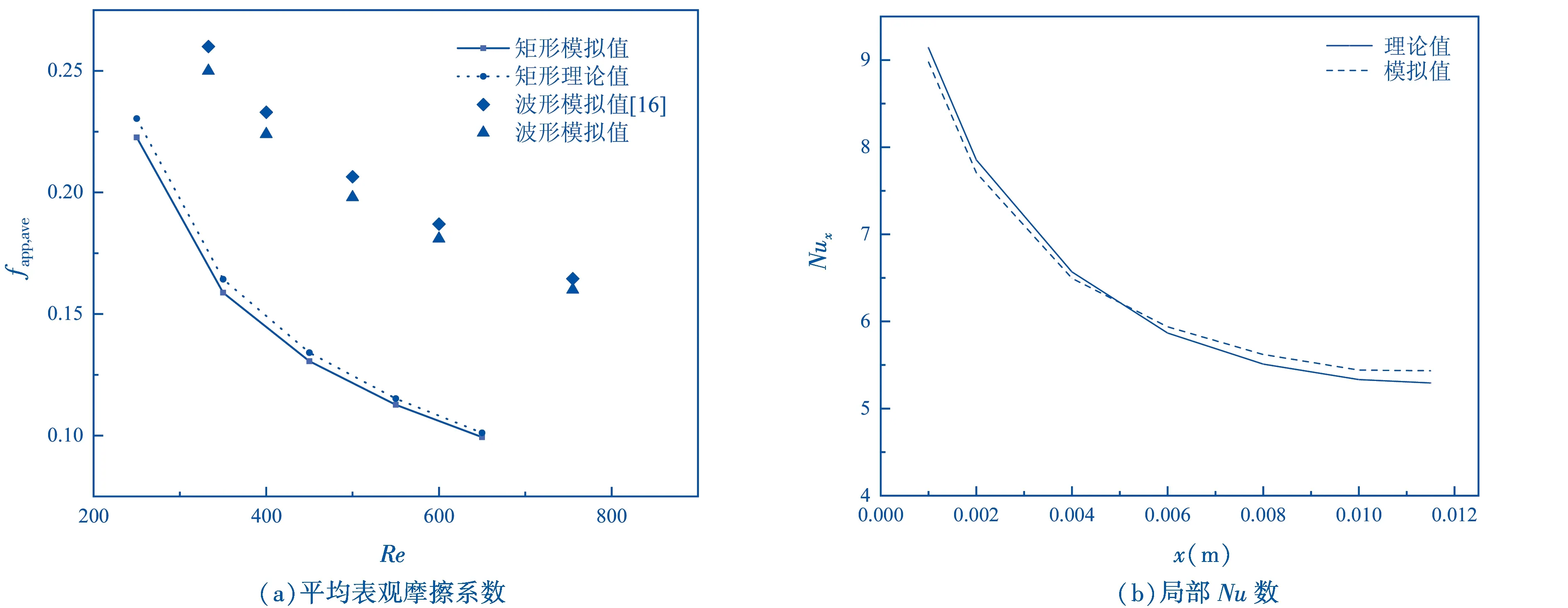
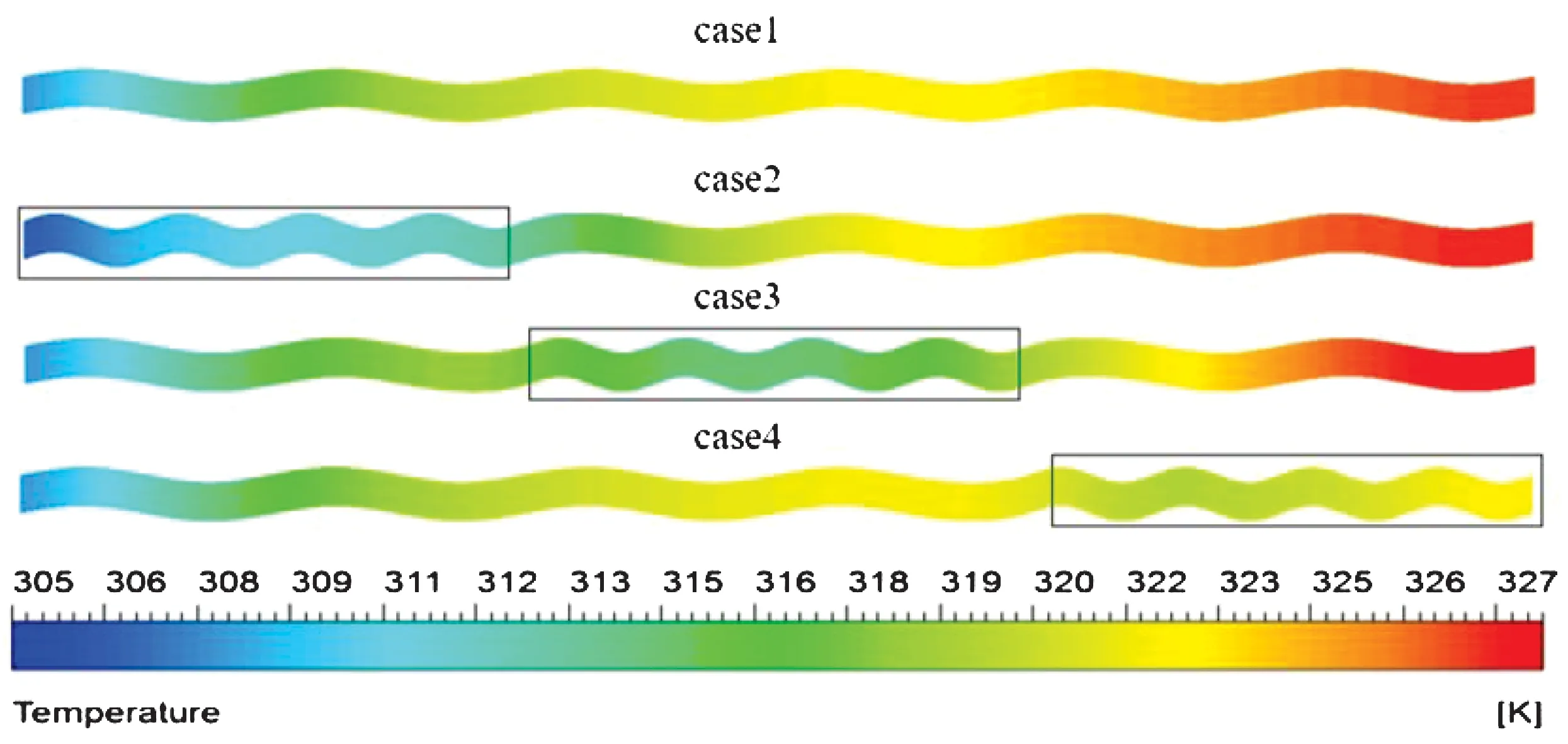
按照通道水力直径Dh对通道尺寸进行划分是比较直观和公认的方法.Kandlikar等[13]认为当10 μm

连续性方程

(1)

动量方程

(2)

能量方程

(3)

λs∇2Ts=0；

(4)

公式中：ρ，cp，λf，λs，μ分别为流体密度，kg/m3，流体的比热容，kJ/(kg·K)，流体导热系数，W/(m·K)，固体导热系数，W/(m·K)和流体动力粘度，kg/(m·s)；Ф为粘性作用所导致的机械能转换为热能的部分，W，称为耗散系数，下标s为固体，f为流体.

边界条件如下：

微通道入口为速度入口边界条件，入口处流体温度为常数；即

x=0，u=uin，T=Tin，

(5)

本文数值模拟中选取uin=1 m/s、1.5 m/s、2 m/s、2.5 m/s、3 m/s，Tin=293 K.

微通道的出口为压力出口边界条件：

x=L，p=pout=0pa，

(6)

微通道计算区域底面为恒热流边界条件，其它表面为绝热边界条件为

(7)

数值模拟中取q″eff=100 W/cm2.

固液接触面为无速度滑移；即

(8)

计算区域y轴方向的两个侧面为周期性边界条件，对称面的法向温度梯度为0；即

(9)

1.3 数值计算方法

本文采用计算流体动力学软件FLUENT15.0进行三维数值模拟.模型中固体材料为硅，流体工质为去离子水.采用有限容积法对控制方程进行离散，采用SIMPLEC算法耦合压力和速度.对流项采用二阶迎风格式进行空间离散化，扩散项选用二阶中心差分格式进行离散.当变量的残差值小于10-6时，认为数值解收敛.

利用数值模拟得到的结果，计算表观摩擦系数fapp，ave，表达式为

(10)

通道水力直径计算为

(11)

通道整体热阻的计算[14]为

(12)

泵功的计算为

PP=ΔpQv；

(13)

通道平均换热系数和Nusselt数的表达式为

(14)

(15)

公式中：△p为通道进出口压降，Pa；ρ为流体密度，kg/m3；L为通道实际长度，m；um为流体平均流速，m/s；Tb，max、Tin分别为通道底面最大温度和进口温度，K；Q、Ab及Acon分别为总传热量，W、通道底面有效加热面积，m2及单根通道的有效传热面积，m2；Tw、Tf分别为通道底面的平均温度，K、流体进出口平均温度，K；Qv为通道内的体积流率，m3/s.

1.4 网格独立性检验

本文采用GAMBIT软件对微通道计算区域进行网格划分.以λ=2 000 μm，A=60 μm传统正弦微通道为例，对网格独立性进行说明.选取了三种代表性网格(稀疏、较密、极密)进行独立性检验.表2为Re=348时，通道的网格独立性检验结果.由此可见选取网格数为1.4百万，相对误差小于1%，既保证了计算结果的精度，又节省了计算时间.

表2 网格独立性检验

1.5 模型有效性检验

为了对数值算法的准确性进行验证，将矩形微通道的数值模拟结果与理论值进行对比；将波纹形微通道的数值模拟结果与文献[16]中的数值模拟结果进行对比.

相同尺寸的矩形微通道的模拟摩擦因数值与理论值的对比如图3(a)所示.对于矩形微通道内发展中的层流流动，Shah 等[14]提出的表观平均摩擦系数表达式为

(16)

公式中：Po为泊肃叶数(Poiseuille number)表达式为

(17)

(18)

相同尺寸的矩形微通道的模拟局部Nu数值与理论值的对比如图3(b)所示.局部Nu数的计算公式[14]为

Nux=Nux，3=Nux，4(Nufd，3/Nufd，4)，

(19)

(20)

(21)

公式中：Nufd，3、Nufd，4、Nux，4分别为传热充分发展时微通道三面加热、传热未充分发展时微通道三面加热和四面加热时的Nu数.由矩形通道的宽高比αc和x*决定，利用线性插值法查表可得[15].

图3 模型有效性验证

2 结果分析与讨论

2.1 流动特性分析

出了入口速度为3 m/s时，矩形直通道和正弦波纹微通道在z=0.3 mm处x-y截面的速度矢量图，如图4所示.从图4中可以看出矩形直通道的流动速度方向基本一致无明显扰动；但正弦波纹微通道中的流体流动方向在波峰和波谷处有明显差异，这主要是由于波形壁面阻碍了流体正常流动，是流体流动方向发生改变，促进流体混合.

图4 z=0.3 mm处x-y截面速度矢量图

矩形直通道、传统正弦波纹微通道和局部加密波纹微通的压降随雷诺数的变化规律，如图5所示.五种通道的压降均随雷诺数的增加而增加.相同雷诺数下，波纹微通道的压降总是大于直通道，这主要是由于随着流速的增加，壁面剪切力和由波状形状引起的形体阻力增大，导致通道内的压降显著增大.三种新型微通道的压降几乎相等，case3的压降较大，case4最小，如局部放大的图所示.这主要是由于尽管流体沿流动方向温度升高，粘度减小；但case3中流体流经中部加密的结构经过两个波形疏密的变化，其局部损失较大.

矩形直通道、传统正弦波纹微通道和局部加密波纹微通道的表观摩擦系数随雷诺数的变化规律，如图6所示.由图6可以看出，随着雷诺数的增大所有通道的表观摩擦系数都减小且减小幅度减小，符合层流流动摩擦系数的变化规律.比较矩形微通道和波纹微通道可以发现，在相同的雷诺数下，后者的表观摩擦系数远大于前者，且新型波纹微通道大于传统正弦波纹微通道.这主要是由于波形壁面的存在增加了体形阻力；减小波长使得流体流过通道时的扰动变大，波形壁面附近的速度梯度增加，壁面剪切力增大；波形壁面使流体产生涡流区也增加了流动阻力.从图中还可以看出加密部位对表观摩擦系数的影响不大.

2.2 传热特性分析

Re=348时，四种波形微通道底面温度云图如图7所示.可以看出case1，和case2，的底面温度沿流动方向逐渐升高，但是后者的平均温度远低于前者.而且随着位置后移温差逐渐变大，但两者的最高温度几乎相等，且后者的底面最低温度小于前者.故case2的设计虽然会减小平均温度，但增大了底面最高温差，引起较大的热应力.如图所示，case3和case4有效的增强了中部和下游的换热，改善了原本沿流动方向底面温度逐渐升高的问题.case3仍没有改善底面温升较大的问题，但case4大幅降低了底面最高温度使底面最大温差有效减小.所以case4不仅可以降低底面平均温度而且使底面最大温差大幅减小.矩形微通道和四种波纹微通道的底面平均温度Tw随入口速度的变化，如图8所示.由图8可以看出，随着入口速度的增加通道的底面平均温度均减小.在相同的流速下，三种局部加密的波纹微通道的底面平均温度小于传统正弦波纹微通道.这主要是由于通道加密的部位换热增强，使整体平均温度降低.相应的微通道底面最大温差ΔTmax随入口速度的变化如图9所示.可以看出case4的最大温差明显小于其它结构.

矩形直通道和四种波纹微通道的Nu数随Re数的变化规律，如图10所示.可以看出，Nu数均随着Re的增加而增加，且波纹微通道的Nu数总是大于相同Re数下的直通道.这主要是由于波形微通道增加了对流换热面积；波形微通道改变了流体的速度分布；波形微通道使流体发生扰动，增强了流体的混合.从图中还可以看出，相同Re数下，改进的三种波纹微通道的Nu数均大于传统正弦波纹微通道，这主要是由于局部加密的微通道使流体混合更加强烈.

图7 通道底面温度云图

2.3 综合性能分析

从上面的分析可知，用波纹微通道代替矩形微通道可以有效的强化换热；局部加密波纹微通道可以提高微通道的换热性能，但是波状结构所带来的压降损失也不能忽略.所以有必要对其综合性能进行评价，热阻是评价散热器能力最直接的指标，泵功是评价系统消耗的直观参数，因此选择泵功与热阻的关系对其综合换热性能进行分析，如图11所示，热阻随着功率的增加而降低.相同泵功下，波纹微通道的热阻总是低于矩形直通道，case2和case3的热阻反而比case1的热阻大.这主要是由于局部加密使微通道的压降增加；同时对上游和中部加密并未改变下游的最高温度.如图所示相同泵功下，case4的热阻远远低于矩形直通道和传统正弦波纹微通道.由此可见对下游加密其强化换热性能大于流动阻力的增大，使微散热器的综合性能得到了明显的提升.