阻感性负载无功功率自适应补偿控制方法＊

唐 旺，翁发禄，王 焕，丁元春

（1.江西理工大学电气工程与自动化学院，江西 赣州 341000；2.江西理工大学资源与环境工程学院，江西 赣州 341000）

电路负载主要包括阻性负载、容性负载及感性负载及三种负载的组合，其中阻感性负载在日常生活中较为常见，例如日光灯、高压钠灯、汞灯、金属卤化灯等。阻感性负载中感性部分不做有用功，进而造成负载视在功率上升，浪费电力资源[1]。为了减小阻感性负载中感性成分的影响，通过一定的电容补偿降低其无功功率是必要的[2]。实际电路中，用电设备的不确定性（例如亮灯数量不确定）造成负载大小不确定，也就是阻感性负载电阻与电容值不确定。当负载变化时，采用统一的定值电容补偿，难达到很好的补偿效果[3]。当电路的负载发生变化时，补偿电容的电容值也应随之变化才能达到好的补偿效果。由于实际负载的电阻与电容值未知且不确定，因此研究电路中电阻与电感值辨识，并通过实时调节补偿电容实现无差补偿具有较好的学术意义及应用价值。本文题出采用自适应策略[4-5]，实时得到电路中负载的电阻与电感值。基于获得的电阻与电感值对补偿电容值进行实时调节，进而实现负载无功功率的无差补偿。同时，通过实例验证了相关成果的有效性。

1 模型描述

无功功率自适应补偿控制模型如图1 所示。L、R为未知负载的电感性及电阻；C为容量连续可调电容，用于补偿系统中的无功功率；e（t）为交流电源。基于电路分析方法，可得图1 系统模型的数学表达如下：

图1 无功功率自适应补偿控制模型

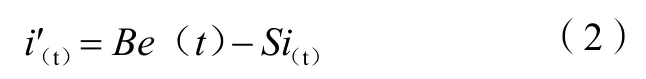
本文原为通过自适应方法辨识参数R和L的值，但是通过R、L、B及S之间的关系可知，如果B及S已知的情况下，可以通过相互关系L=B－1，R=S/B计算出相应R及L的值，因此，下文主要考虑的是参数B及S的辨识。

2 无功功率自适应补偿控制

现假定一系统模型如式（3）所示，其结构与系统模型描述（2）相同，其中为可调节参数（其初始值可任意给定）：

3 实例

假定图 1 所示系统模型参数e（t）=314sin（100×π）t，系统初始时刻负载的电感L1=0.03 H，电容R1=10 Ω。可知未采用电容实现无功功率补偿前的功率因数角为：

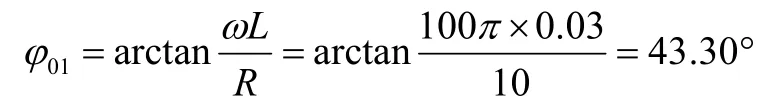
功率因数cosφ01=0.73。当系统运行到100 s 时负载发生变化，负载电感与电容分别变化为L2=0.029 H，R2=8 Ω，此时功率因数角为：

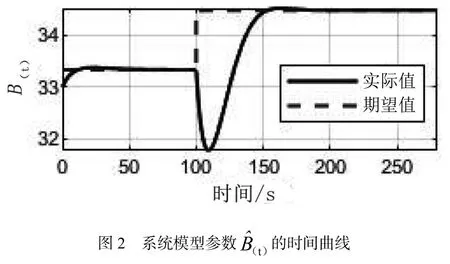
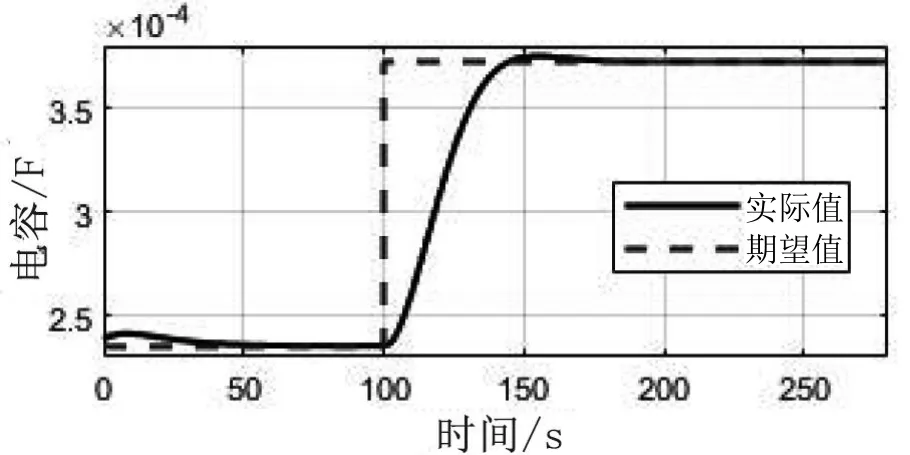
图4 无功功率补偿电容值C（t）的时间曲线

现考虑调节参数α及β对系统响应的影响。α及β分别取如下 4 组值：α=10 000，β=250；α=20 000，β=500；α=40 000，β=1 000；α=80 000，β=2 000，经计算机仿真得到各组参数情形下的系统无功功率补偿电容值C（t）的时间曲线如图5 所示。由图5 可知，参数值减小时，系统无功功率补偿电容值C（t）的上升时间增加，而参数值增大时，C（t）的上升时间减小，但超调增大。也就是说，通过合适选择α及β提升无功功率补偿电容值的调节效率，改变补偿电容对负载变化的响应速度。

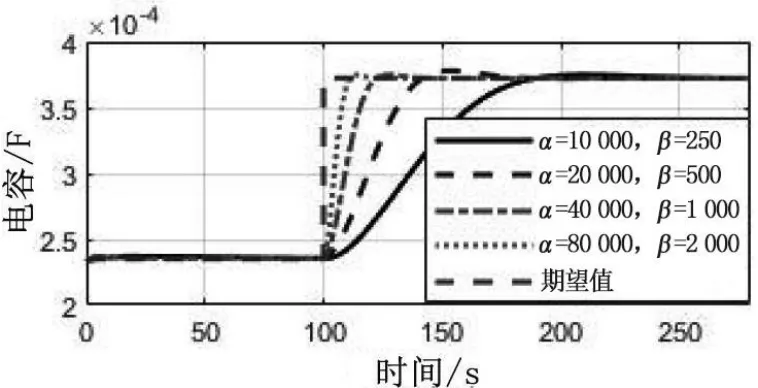
图5 α及β取值对无功功率补偿电容值C（t）的影响

4 结论

本文采用参数自适应方法实现了对电力系统阻感性负载电阻及电感值的辨识。基于辨识得到的电阻及电感值，通过实时调节补偿电容的容量，使负载的功率因数达到用户的设定值，并通过实例验证了其有效性。

本文所得的理论可以用于调节日常感性负载的功率因数，使负载的无用功率降低，效率得到一定提升，有利于电力系统的节能。与传统的固定容量补偿方法相比较，本文所提到的方法可以实现精确补偿，节能效果得到有效提升。