基于JVC的紧凑型地波雷达海上目标点迹-航迹最优关联方法

戴永寿 马 鹏 孙伟峰* 刘培学 纪永刚 庞真真

①(中国石油大学(华东)海洋与空间信息学院 青岛 266580)

②(自然资源部第一海洋研究所海洋物理与遥感研究室 青岛 266061)

1 引言

高频地波雷达(High Frequency Surface Wave Radar，HFSWR)利用3～30 MHz垂直极化电磁波沿海面绕射传播衰减小的特点，可以实现对海上船只与低空飞机等移动目标和海洋动力参数的大范围连续监测[1,2]，具有超视距、全天候、低成本等优点，已经成为一种重要的海上目标监测手段。目标探测用的地波雷达一般采用大型阵列式接收天线，其选址、部署与维护的难度大，限制了其推广应用。因而，发展紧凑型地波雷达系统及相应的目标探测技术成为一个新的发展方向[3]。目前，有两种典型的紧凑型地波雷达系统，一种采用单极子/交叉环天线，例如，CODAR公司的SeaSonde系统[4]，武汉大学研制的OSMAR系统[5]等。另一种采用小型阵列式(3-8阵元)接收天线，例如，Helzel Mess-Technik公司的WERA-S系统[6]，我们团队研制的CORMS紧凑型地波雷达系统[7—9]等。紧凑型地波雷达系统占地面积小，部署灵活，维护方便，可以将其部署在海岛或者船只平台上，拓展其应用范围。然而，由于接收天线阵列孔径减小且发射功率降低，紧凑型地波雷达对目标方位角的估计精度降低，目标探测时的信噪比低，虚警率高，给目标检测与跟踪带来了很大的挑战。

目标跟踪是一个由数据关联和状态估计构成的循环过程。作为目标跟踪算法的关键环节，点迹-航迹关联方法从雷达最新获取的来自多个目标与杂波的量测点迹数据中识别出属于已形成航迹的目标点迹，其性能的优劣将直接影响目标跟踪的结果。在密集杂波环境下进行多目标跟踪时，由于雷达探测精度降低，常常出现因错误的点迹-航迹关联导致的航迹断裂现象。因此，如何实现准确的点迹-航迹关联成为紧凑型地波雷达目标跟踪的一个关键问题。目前，应用于紧凑型地波雷达的点迹-航迹关联算法可分为两类：一类基于目标的空间状态信息计算航迹与点迹之间的关联程度[10]，典型算法有最近邻数据关联算法 (Nearest Neighbor Data Association,NNDA)[11]、全局最近邻数据关联算法(Global Nearest Neighbor Data Association,GNNDA)[12]、概率数据关联算法 (Probabilistic Data Association,PDA)[13]、联合概率数据关联算法(Joint Probabilistic Data Association,JPDA)[14]等。另一类是基于模糊数学和神经网络的方法，这类方法通过选定关联隶属度，并计算点迹与航迹之间的隶属值来确定航迹是否与点迹关联[15]，典型算法有模糊关联算法[16]和神经网络关联算法[17]等。上述方法中，最近邻关联算法适用于目标稀疏的情况，在目标密集、航迹交叉等应用场景中，使用最近邻关联算法极易发生误关联。文献[11]将联合概率数据关联引入最近邻算法提出了联合最近邻数据关联算法，在保持高计算效率的同时，关联精度达到了联合概率数据关联的水平。文献[12]利用全局最近邻关联算法实现了静轨光学卫星与自动识别系统 (Automatic Identification System,AIS)目标点迹的关联，校正了系统误差。文献[13]分析了真实场景中杂波对目标跟踪的影响，利用PDA算法实现了密集杂波环境下的多目标跟踪。文献[14]利用AIS对双频高频地波雷达系统误差进行校正，并结合JPDA算法与无味卡尔曼滤波算法实现了海上舰船目标的精确跟踪。文献[16]将不同量测点迹与目标间的隶属度作为模糊关联概率，结合模糊关联概率与卡尔曼滤波算法，实现了杂波环境下的多目标跟踪。文献[17]将多目标跟踪过程中的点迹-航迹关联问题转化为旅行商问题，应用Hopfield神经网络实现了密集目标环境下的点迹-航迹关联，在保证关联性能的同时提高了算法的运行效率。

综上所述，国内外学者已经提出了多种方法来解决多目标跟踪过程中的点迹-航迹关联问题，但现有关联方法大都采用序贯的方式进行，很少有工作从全局最优的角度考虑多目标情形下的点迹-航迹分配，容易引起航迹间的关联竞争导致航迹断裂、误跟踪等现象发生，这个问题在紧凑型地波雷达目标跟踪中变得尤为突出。为了解决上述问题，本文将紧凑型地波雷达获取的较准确的多普勒速度与目标的距离和方位角一起作为表征目标状态的参数，结合对各参数的测量误差分析，采用最小代价函数确定候选点迹与目标航迹之间的相似程度，形成关联代价矩阵；然后利用JVC(Jonker-Volgenant-Castanon)算法求解全局最小关联代价，将最小关联代价对应的点迹-航迹组合作为最优的点迹-航迹分配结果。利用仿真及实测数据开展了点迹-航迹关联实验，结果验证了所提方法的有效性。

2 基于JVC算法的点迹-航迹最优关联方法

2.1 目标状态参数的选择

地波雷达在以雷达位置为坐标原点的极坐标系下表示目标，除了可以获取目标的距离和方位角参数外，还可以得到目标的多普勒速度。目标的位置由距离和方位角共同决定，由于紧凑型高频地波雷达接收天线阵列孔径减小导致对目标探测时的空间分辨率低，如果仅以距离和方位角参数作为目标状态进行点迹-航迹关联，在局部点迹密集区域很容易造成误关联。

紧凑型地波雷达对海上船只目标探测时往往采用较长的积累时间，因而能够获得较高分辨率的多普勒速度，可以将其与距离和方位角参数一起作为目标的状态参数，提升对目标的表征能力。因此，本文将k时刻雷达获取的一个目标量测点迹表示为，其中，分别表示k时刻目标的多普勒速度、距离和方位角，[·]T表示转置操作。

2.2 最小关联代价的计算

其中，σvr,σr和σθ分别代表多普勒速度、距离和方位角3个运动学参数的标准差，Wvr,Wr和Wθ表示3个参数的关联权重，依据3个参数的分辨率高低设置，需满足式(8)的条件

2.3 基于JVC算法的点迹-航迹最优分配

式(11)表示任意一个候选点迹最多与一条航迹关联，式(12)表示任意一条航迹最多与一个候选点迹关联。

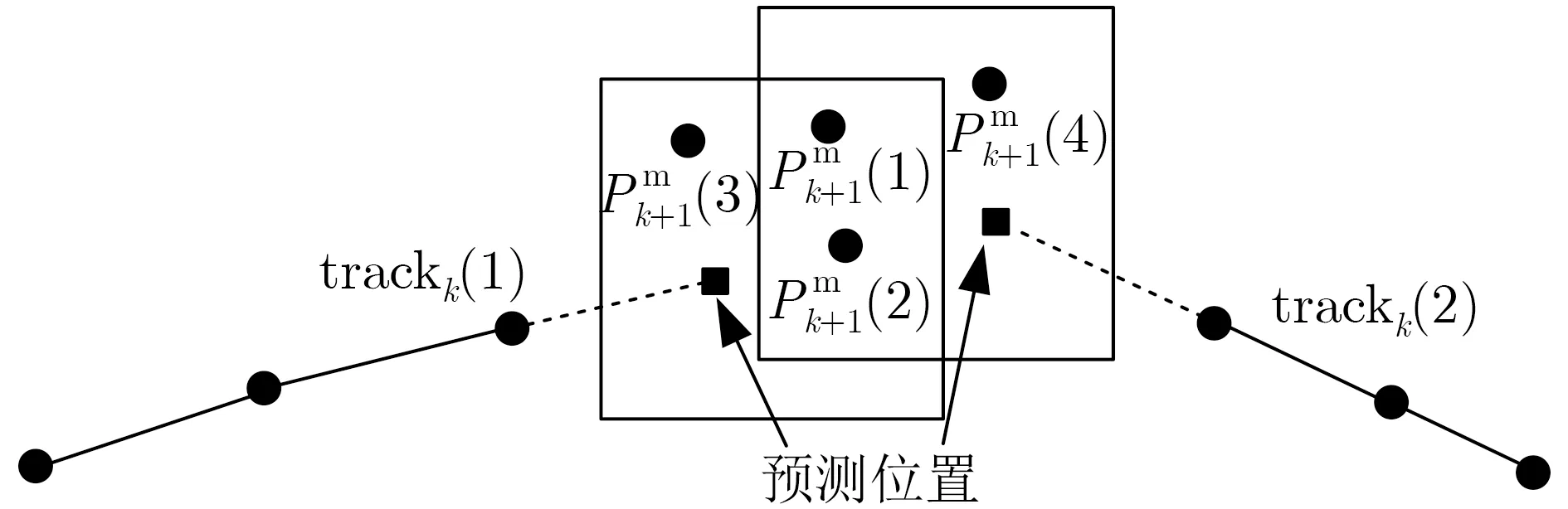
图1 关联波门示意图

常用的最优分配方法有Munkres算法、Auction算法和JVC算法。其中，Munkres算法与JVC算法的最优分配效果优于拍卖算法，且JVC算法具有最高的计算效率[19]，因此，本文选择采用JVC算法求解最优的点迹-航迹关联组合。

综上，本文提出的基于JVC算法的点迹-航迹最优关联方法的流程总结如下：

输入：存在公共候选点迹的M条航迹以及其波门内的N个候选点迹

输出：点迹-航迹最优关联结果

算法步骤：

(2)基于关联代价矩阵D，利用JVC算法求解式(13)，得到关联总代价Δ最小时的点迹-航迹关联组合。

(3)利用最佳点迹-航迹组合中的候选点迹与对应预测点迹进行滤波处理，用滤波结果更新对应的目标航迹；当航迹数目大于或等于候选点迹数目(M ≥N)时，采用预测点迹更新没有被分配到候选点迹的目标航迹。

3 实验分析

为了评价本文提出的点迹-航迹关联方法的性能，分别利用仿真及实测目标数据，以转换坐标卡尔曼滤波算法作为基本的跟踪方法，分别应用序贯式最近邻数据关联方法(NNDA)及本文提出的最优关联方法进行点迹-航迹关联，利用跟踪时长、关联准确性等指标对关联结果进行评价。

3.1 仿真实验

选择5批邻近行驶且存在多目标航迹交叉、单目标航迹转圈的场景开展仿真实验，设置数据率为1帧/分钟，5批航迹在以雷达位置为原点的极坐标系下的初始距离、方位角、多普勒速度以及包含的帧数等参数如表1所示。

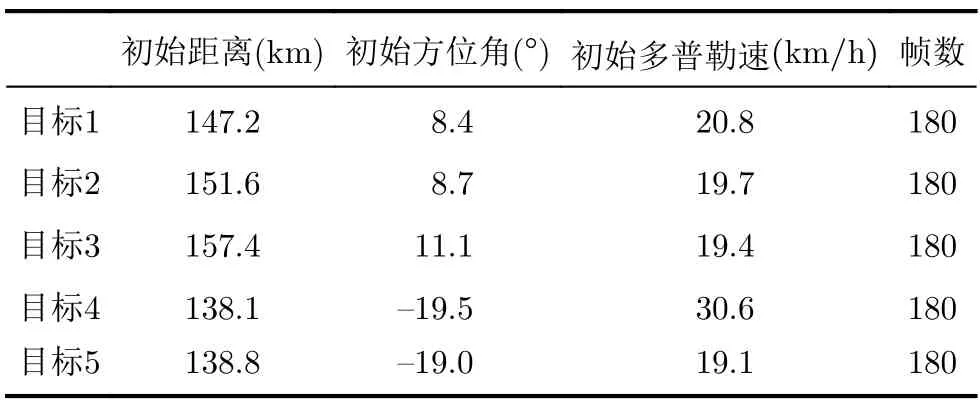
表1 仿真目标的参数

根据紧凑型地波雷达目标探测时不同参数的误差范围，分别给距离、方位角、多普勒速度加入不同强度的高斯白噪声，并在观测区域内加入服从泊松分布的杂波，得到仿真场景，如图2所示。黑色点迹代表杂波，红色点迹代表目标航迹起始位置。分别用序贯最近邻关联方法、本文提出的关联方法作为点迹-航迹关联方法，跟踪得到的航迹结果示于图3中，图中标注位置为航迹起始点。

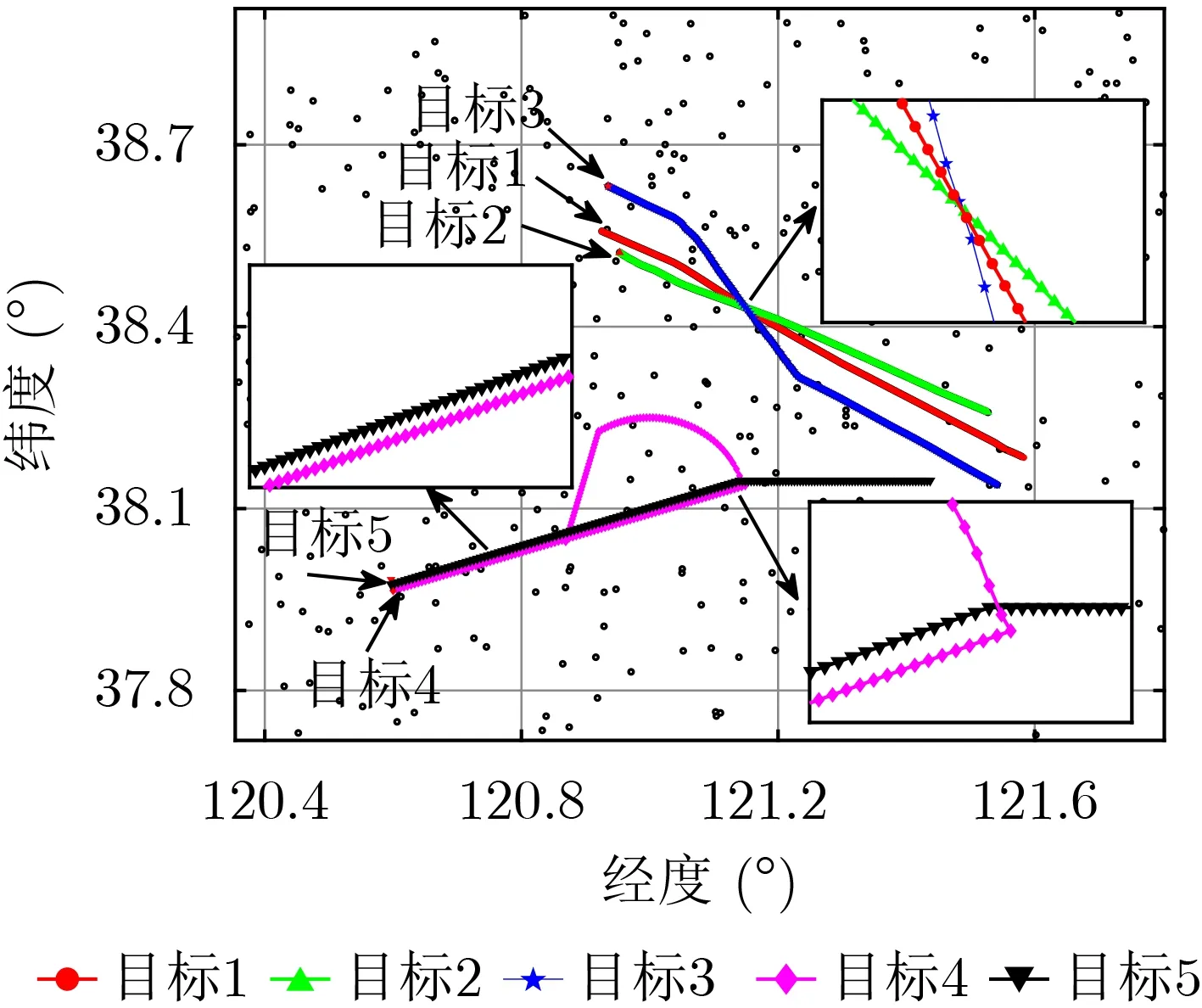
图2 紧凑型HFSWR目标仿真示例

由图3的跟踪结果可以看出，对于大部分数据帧，两种关联方法均能够关联到正确的点迹。在第64帧时，目标航迹1、航迹2、航迹3与其相对应的3个候选点迹之间的关联代价矩阵为

图3 基于仿真数据的跟踪结果对比

其中，∞表示点迹位于目标航迹的关联波门之外，即目标1、目标2的点迹不可能与目标3的航迹关联。由关联矩阵D可知，采用序贯最近邻关联方法时，目标航迹1、航迹2分别与关联代价更小的目标2的点迹、目标3的点迹关联，导致目标航迹3在该时刻无点迹关联，发生了航迹断裂。本文方法在总关联代价最小的约束条件下寻找最优的“点迹-航迹”关联组合，当总关联代价取最小值0.0089+0.4669+0.4402=0.916时，恰好对应正确的点迹-航迹关联组合。类似地，在第100帧时，目标4发生转弯机动，序贯最近邻方法因关联错误导致目标航迹4与航迹5均发生了航迹断裂现象，而本文方法使目标航迹4与航迹5均关联到了正确的点迹，提高了航迹跟踪的连续性。通过以上分析可知，本文方法解决了多批目标跟踪过程中由于序贯式处理导致的误关联问题，实现了对多批目标航迹的准确、持续跟踪。

3.2 实测数据实验

利用课题组研制的CORMS紧凑型地波雷达系统于2019年1月18日在中国威海附近海域进行了目标探测实验。该雷达系统的工作频率为4.7 MHz，采用8阵元紧凑型接收天线阵列，天线孔径为105 m，数据率为1帧/min，从11:04至15:29共采集266帧数据。

3.2.1 地波雷达目标参数准确性分析及参数选择

为了分析研制的紧凑型地波雷达获取目标参数的准确性，选取利用实测数据跟踪得到的10条雷达航迹(共包含830个点迹)，采用航迹关联方法[20]找到与其关联的AIS航迹，分别计算两者之间的多普勒速度、距离和方位角误差，误差统计结果如图4所示。

由图4的结果可以看出，所用紧凑型地波雷达系统的多普勒速度、距离和方位角的测量误差分别为1km/h,1.5km,5°。在实测数据跟踪实验中，将多普勒速度、距离和方位角3个运动学参数的标准差,σr与σθ分别对应设为上述数值。可见，多普勒速度与距离的测量误差较小，而方位角的探测精度很低，与2.1节的分析结果一致。

图4 目标参数误差分析

3.2.2 关联结果分析

分别采用序贯最近邻方法与本文方法作为点迹-航迹关联方法，利用实测数据进行目标跟踪得到目标航迹。由于跟踪时长能够反映跟踪航迹的连续性，分别统计跟踪时长大于30 min、大于40 min、大于50 min的航迹数目，统计结果如图5及表2所示。对比图5与表2中的结果可知，采用本文提出的关联方法在3个跟踪时长范围内的平均跟踪时长明显提升。为了进一步分析关联准确性及航迹数量与跟踪时长差异的原因，选取3个实测目标个例进行分析，目标个例的详细信息如表3所示。

表2 不同跟踪时长的航迹数量对比

表3 目标个例详细信息

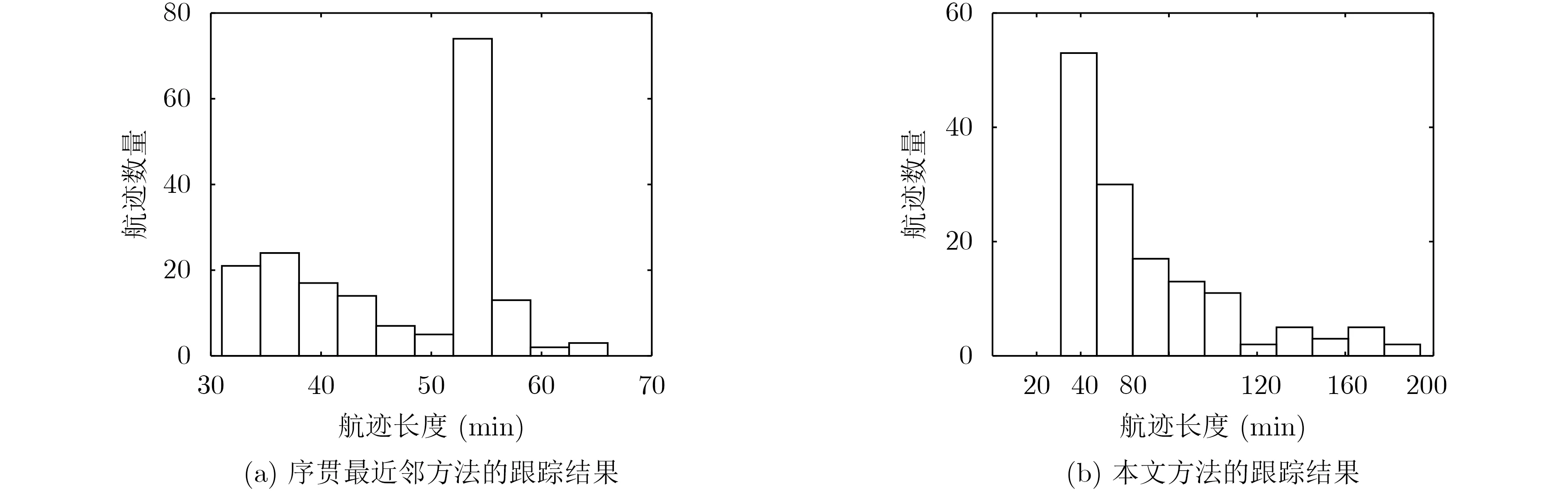
图5 采用实测数据跟踪时不同时长的航迹数目对比

采用序贯最近邻关联方法得到的航迹个例1、个例2及个例3与AIS 航迹对比结果如图6(a)所示，雷达航迹与AIS航迹在航迹起始位置处用黑色虚线连接。可以看出，由于序贯最近邻方法出现误关联，航迹1、航迹2与航迹3分别在54 min,50 min与56 min时发生了断裂，整体跟踪时长较AIS航迹短。采用本文方法得到的航迹与AIS航迹的对比情况如图6(b)所示，对比可见，对于3条目标航迹，本文方法解决了误关联的问题，修复了断裂的航迹，跟踪时长分别提高至124 min,180 min与150 min。值得注意的是，航迹2与航迹3在60～70 min的跟踪时段内出现了交叉现象，采用本文方法可以避免误关联现象的发生，进一步验证了提出方法的有效性。

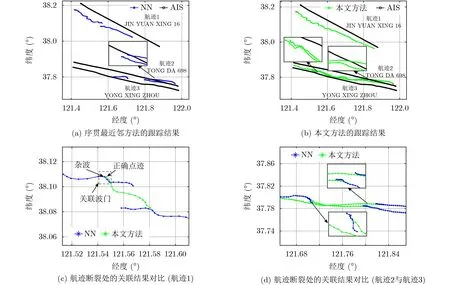
图6 采用实测数据的跟踪结果对比

为了进一步对比两种方法的关联效果，图6(c)、图6(d)分别画出了航迹个例1、个例2与个例3在航迹断裂前后时刻的点迹-航迹关联情况。可见，采用序贯最近邻关联方法得到的航迹1、航迹2与航迹3分别在44 min,43 min与49 min时关联到错误点迹，导致目标航迹偏离正确的航行轨迹，进一步使得航迹在后续时刻关联到杂波或其他目标的点迹，从而导致航迹断裂。采用本文方法能够准确关联到正确的目标点迹，且跟踪时长更接近目标真实运动时长，提升了航迹跟踪的连续性。

3.2.3 计算速率与关联准确性统计分析

为了验证本文提出方法的计算速率与关联准确性，分别采用序贯式最近邻点迹-航迹关联方法(NNDA)与本文方法，利用266帧实测数据进行了200次蒙特卡罗目标跟踪实验。从跟踪结果中选择了54条目标航迹，采用航迹关联方法[20]找到与其关联的AIS航迹进行点迹-航迹关联准确性分析，实验结果如表4所示。

表4 采用两种方法时的跟踪结果比较

由表4的结果可以看出，本文方法的运行时间较序贯最近邻方法稍长，但均满足工程上对目标跟踪实时性的要求。与序贯最近邻关联方法相比，本文方法的关联准确率从53.7%提升至81.5%。可见，本文方法在满足工程实时性要求的同时，大幅提升了点迹-航迹关联的准确性。

4 结束语

针对多目标跟踪算法中采用序贯式的点迹-航迹关联方式易发生误关联导致航迹断裂、误跟踪等问题，结合紧凑型地波雷达获取目标参数的特点，提出了一种基于JVC算法的点迹-航迹最优关联方法，在总关联代价最小准则的约束下实现了紧凑型地波雷达点迹与航迹间的最优匹配。仿真与实测数据点迹-航迹关联实验结果表明，本文所提点迹-航迹最优关联方法能够解决航迹跟踪过程中因错误关联导致的航迹断裂问题，提高目标跟踪的连续性。

需要指出的是，紧凑型地波雷达在目标探测时，不仅空间分辨率低，检测概率也较低，在某些时刻会大概率存在目标漏检的情形，目标漏检也会导致航迹断裂问题的发生，可考虑采用双站/多站组网的方式，综合多站目标探测结果以提高目标检测概率的方式来解决，目前正在开展这项研究工作。