时-空变化的背景电离层对星载合成孔径雷达方位向成像的影响分析

张永胜 计一飞 董臻

(国防科技大学电子科学学院 长沙 410073)

1 概述

星载合成孔径雷达(Synthetic Aperture Radar,SAR)是一种主动式微波遥感系统，集全天时、全天候、多波段、多极化等特点于一身，具有其他遥感系统难以发挥的作用，已在环境监测、灾害监测、海洋监测、资源勘探、农业估产、城市规划、测绘和军事侦察等领域发挥重要作用。为了提供更广阔、更丰富、更细致的对地观测信息，星载SAR正逐渐覆盖各个典型波段，并朝着高时空分辨率、宽测绘带等方向发展[1]。由于低波段系统 (包括L波段和P波段)表现出对生物量的高敏感性[2–4]，以及对叶簇、浅层地表和伪装覆盖物的强穿透力[5–7]，利用低波段星载SAR实现生物量反演、碳循环监测以及隐蔽目标探测已成为一个新的研究热点。另外，随着广域目标区域长时间连续观测的需求不断增长，众多国内外学者和科研机构针对中高轨SAR开展了理论研究和系统论证[8–10]。

SAR卫星一般运行于距离地面200 km以上的轨道，而电离层分布于距离地面60～2000 km，这些星载SAR的电磁波信号在发射和反射的传播过程中势必会穿过电离层，从而受到电离层的影响，主要包括时延、相位超前、色散、折射、衰减、法拉第旋转以及闪烁等效应，最终对星载SAR2维图像及其应用造成影响。电离层通常可以分为随机性、中小尺度分布的不规则体以及确定性、时空缓变、大尺度分布的背景电离层两个部分[11]。前者引入的信号幅度和相位闪烁将会导致合成孔径内的去相干效应，从而造成方位向图像散焦[12–14]；后者引入的相位超前误差会影响星载SAR干涉性能，群延迟会导致图像整体偏移，色散效应主要会导致距离向图像散焦，FR效应会导致极化测量误差[11]，本文研究的是背景电离层的影响。研究表明，随着星载SAR系统载频的降低、带宽的增大以及合成孔径时间的增加，电离层效应更加显著[15–17]。

随着近年来针对中高轨SAR系统的研究不断深入，尤其是对于地球同步轨道SAR(GEO SAR)，其超长合成孔径时间内时空变化的背景电离层受到了广泛关注。2014年，李亮等人[18]通过引入电子总量(TEC)关于方位时间的各阶导数，初步考虑了时变背景电离层对中高轨SAR方位向成像的影响。同年，李雨龙等人[19]利用Ishimaru的广义模糊函数模型，结合国际参考电离层(International Reference Ionosphere, IRI)研究了背景电离层时空变效应对GEO SAR成像的影响。北京理工大学的研究团队深入考虑了时变背景电离层对GEO SAR方位向成像的影响[20–23]，详细推导了时变TEC导致的方位相位压缩误差、距离单元迁徙误差以及二次距离压缩误差[21]，并给出了背景电离层时变参数对GEO SAR方位聚焦影响的容限曲线，同时利用全球定位系统、北斗导航卫星接收机实测得到的电离层TEC数据进行了信号级、图像级的仿真[21–23]，从而验证了理论推导的有效性。另外，孔径内传播路径变化引起的时变斜距电子总量(Slant Total Electron Content, STEC)对星载SAR方位向成像的影响也受到了一些学者的关注[24,25]。

在建立背景电离层对星载SAR方位向成像影响的信号模型时，上述文献大多仅考虑了背景电离层垂向电子总量 (Vertical Total Electron Content,VTEC)的时变因素。但由于星载SAR的下视观测几何，最终需要考虑STEC，而合成孔径时间内STEC的变化与方位时间、背景电离层穿刺点的位置以及传播路径都有关系，这表明孔径内方位时变的STEC源于时-空变化耦合的背景电离层以及传播路径的变化。因此，本文将针对导致方位时变STEC的3个具体因素，即VTEC的时间变化和空间变化，以及电磁波传播路径的变化，分析不同星载SAR系统方位向成像性能受到的影响。

2 方位向信号模型

考虑时空变背景电离层的影响，则星载SAR系统冲激响应函数可表示为[20,21,25]

其中，fτ为快时间τ对应的距离频率，η为方位慢时间，fc为载频，c为光速，Kφ≈40.28为电离层常数，rx,ry表示背景电离层穿刺点位置坐标，该穿刺点为方位时刻η卫星、点目标P的连线与背景电离层相位屏的交点，h0(fτ,η;P)为点目标P对应的理想冲激响应函数，Wr为距离频域窗函数，wa为方位时域窗函数，ηP为P的方位中心时刻，Kr为距离向调频率，RP(η)为斜距历程。而孔径内方位时变的STEC可近似表示为以下3阶多项式的形式[25]

由于本文研究方位向成像性能，因此可以忽略电离层相位误差对距离频率的依赖性，给出方位时域信号的表达式

其中，R0为中心斜距，p1,p2,p3分别为距离历程关于方位时间的1阶、2阶、3阶系数。根据驻定相位原理，可以求得方位时间关于多普勒频率fη的3阶驻相解

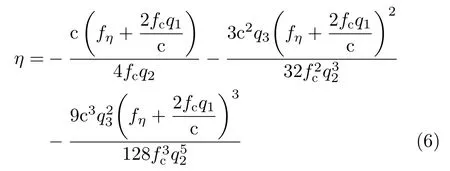
其中，qn=pn-，n= 1,2,3。将式(6)代入式(4)的指数项，并去除零阶项，则方位压缩相位有如式(7)的3阶泰勒展开式

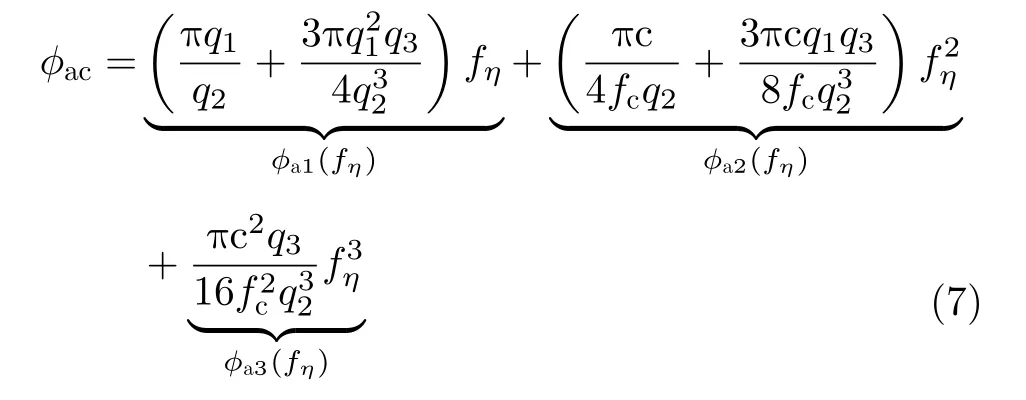
可见k1,k2,k3的存在改变了方位压缩相位，从而造成方位向1次、2次、3次相位误差。为便于后期数值计算与分析，在推导方位向偏移、2次相位误差(QPE)和3次相位误差(CPE)时，可以忽略1/q2高 阶项对相位误差的贡献，并且取1 /q2≈1/p2,因此由1次相位误差导致的方位向偏移可以表示为

其中，vg为SAR卫星波束中心扫过地面的速度，即地速。在条带模式下，设计方位分辨率(不加窗)可以表示为ρa=0.886vg/Ba，其中Ba=KaTa为多普勒带宽，Ta为合成孔径时间，Ka=4fcp2/c表示多普勒调频率。故方位向偏移可进一步推导为

通过计算多普勒带宽边缘与中心的相位误差之差，可分别得到方位向QPE和CPE表达式

当前，信息化的技术和装备正逐渐成为社会发展变革的重要推动力。以人工智能、大数据为代表的技术层面的探索，已经被确定为国家重大发展战略。在农业生产领域加强植保大数据建设，既是对国家重大战略的落实，也是提高病虫害监控能力的有力举措。

根据式(10)和式(11)，方位向QPE和CPE都依赖中心频率以及合成孔径时间，且分别与,成正比。

3 导致STEC方位时变的3个因素

时变STEC是由VTEC的时间和空间变化，以及传播路径变化导致的，故式(3)中时变STEC的各阶系数来源于这3个因素的耦合作用，因此接下来将针对这3个因素展开分析。

3.1 时变VTEC

单独考虑VTEC时变的因素，则式(3)可简化为

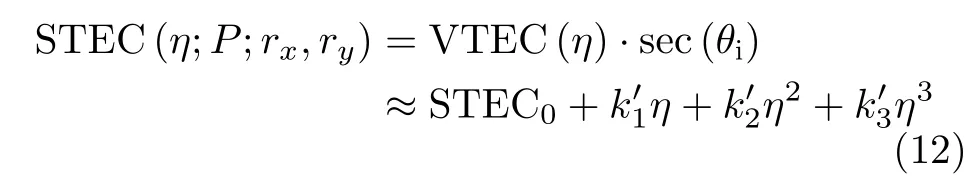
这里利用中国电子科技集团电波传播研究所提供的两组实测VTEC数据，单独分析时变VTEC 因素导致的时变STEC。两组数据分别于2001-12-15,2007-12-15的海口地区测得，数据采样间隔为300 s，可以通过插值得到采样间隔为1 s的数据。不妨设置一个100 s的滑动窗，每次滑动取窗内的VTEC数据，并通过多项式拟合得到时变VTEC的常量以及时变分量的1阶、2阶、3阶系数，拟合结果如图1所示。由于2001年为太阳活动极大值年份，因此从整体来看，该年VTEC常量以及各阶系数相比于极小值年份的2007年具有更大的值。根据图1(b)、图1(c)，并结合现有文献中关于时变背景电离层的描述[20–23]，可以认为时变VTEC 1阶、2 阶、3 阶系数的绝对值一般不会超过0.0 0 5 TECU/s,5×10–6TECU/s2,5×10–9TECU/s3。考虑入射角小于60°的情况，那么由时变VTEC主导的STEC 1阶、2阶、3阶系数(分别为)的绝对值一般不会超过0.01 TECU/s,1×10–5TECU/s2,1×10–8TECU/s3。

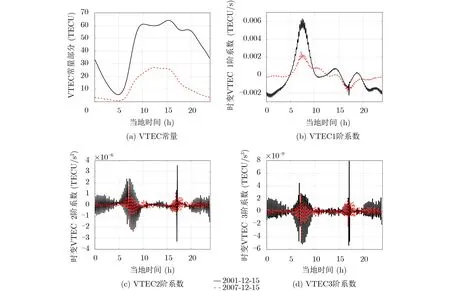
图1 实测 VTEC 数据各阶分量的拟合结果

3.2 空变VTEC

星载SAR合成孔径在背景电离层高度的投影通常在几千米至几十千米量级，因此中尺度的背景电离层空间分布在星载SAR合成孔径内主要表现为VTEC的线性变化，从而导致孔径内STEC随方位时间线性变化。单独考虑VTEC空变的因素，则式(3)可简化为

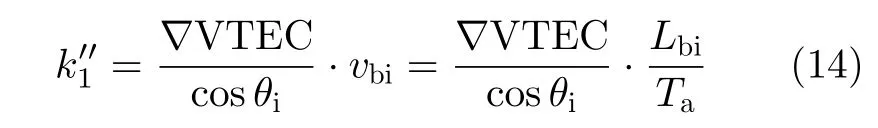
其中，∇VTEC 表示VTEC的空间变化率，vbi为孔径内背景电离层穿刺点的速度，Lbi为合成孔径在背景电离层高度的投影。

基于IRI模型，图2给出了某区域的VTEC2维空间分布，该区域位于北纬13.8°～22.8°、东经104.6°～114.0°，输入时间为2001年12 月15日17时，图中VTEC极小值、极大值分别为44.5 TECU,61.2 TECU，且两者位置大约相距1200 km，由此可知∇VTEC可达0.014 TECU/km。对于LEO SAR(轨道高度700 km)来说，取θi为60°的远端波位情况，vbi通常可达3.5 k m/s，故极大值约0.1TECU/s；对于中轨SAR(MEOSAR)来说，其轨道高度设为7000km,vbi约0.2 km/s，故极大值约0.005 TECU/s；对于GEO SAR来说，若取轨道倾角为60°，离心率为0，纬度幅角为0，那么vbi仅30m/s,极大值小于10–3TECU/s。由此可见，该因素在低轨情况下最为突出，而在中高轨情况 下对应的值很小。

图2 IRI给出的局部区域 VTEC2 维分布(单位：TECU)

3.3 传播路径变化

这里不考虑VTEC的时空变效应，仅考虑传播路径变化，则该因素导致的时变STEC可以近似表示为

4 数值分析

4.1 成像合成孔径时间

由于时变STEC导致的方位向QPE,CPE均与合成孔径时间有关，因此这里进一步研究不同星载SAR系统的合成孔径时间，而合成孔径时间可严格定义为

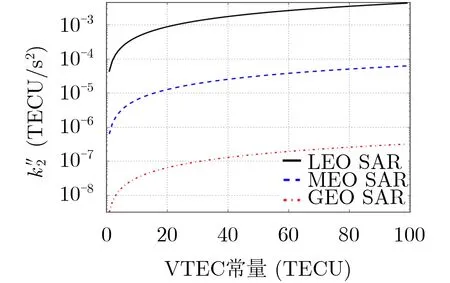
图3 传播路径变化引入的时变STEC 2阶分量系数

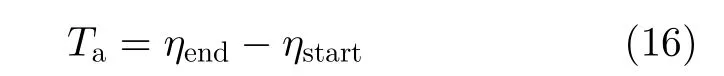
其中，ηstart,ηend分别为3 dB波束开始和结束照射目标的时刻。在低轨情况以及中高轨的某些轨道位置下，合成孔径时间也可以近似表示为

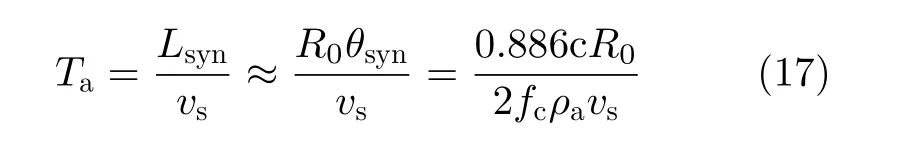
其中，θsyn=0.886c/(2fcρ2)为合成孔径角，vs表示地心固连坐标系下的卫星速度。由于轨道越高，中心斜距R0越 大、星速vs越小，那么合成孔径时间与轨道高度呈正相关关系。另外，对于GEO SAR的大多数轨道位置，由于地球自转效应的突显，合成孔径时间在不同纬度幅角位置上有一定差异，而式(17)不再适用。

基于式(17)，图4(a)计算了不同波段、不同轨道高度、不同设计方位分辨率情况下的合成孔径时间，入射角统一设置为30°，方位分辨率变化范围为0.5～10 m，GEO SAR设置轨道倾角为60°，离心率为0，纬度幅角为0，MEO SAR轨道高度为7000 km，其余轨道参数与GEO SAR一致。对于载频为500 MHz的P波段LEO SAR系统，0.5 m,1 m,2 m的设计方位分辨率对应的合成孔径时间分别大约为55 s,28 s,14 s；对于现有L波段LEO SAR高分辨模式，即PALSAR-2的聚束模式，方位分辨率为1 m，对应的合成孔径时间约10 s。在给定中心频率和方位分辨率情况下，轨道越高，合成孔径时间越长，GEO SAR的合成孔径时间可达几百甚至上千秒。基于式(16)，图4(b)进一步给出了不同波段GEO SAR合成孔径时间随纬度幅角的变化曲线。可见，在纬度幅角为90°附近，合成孔径时间会突然增大，这主要是因为此时卫星与地面的相对速度很小。

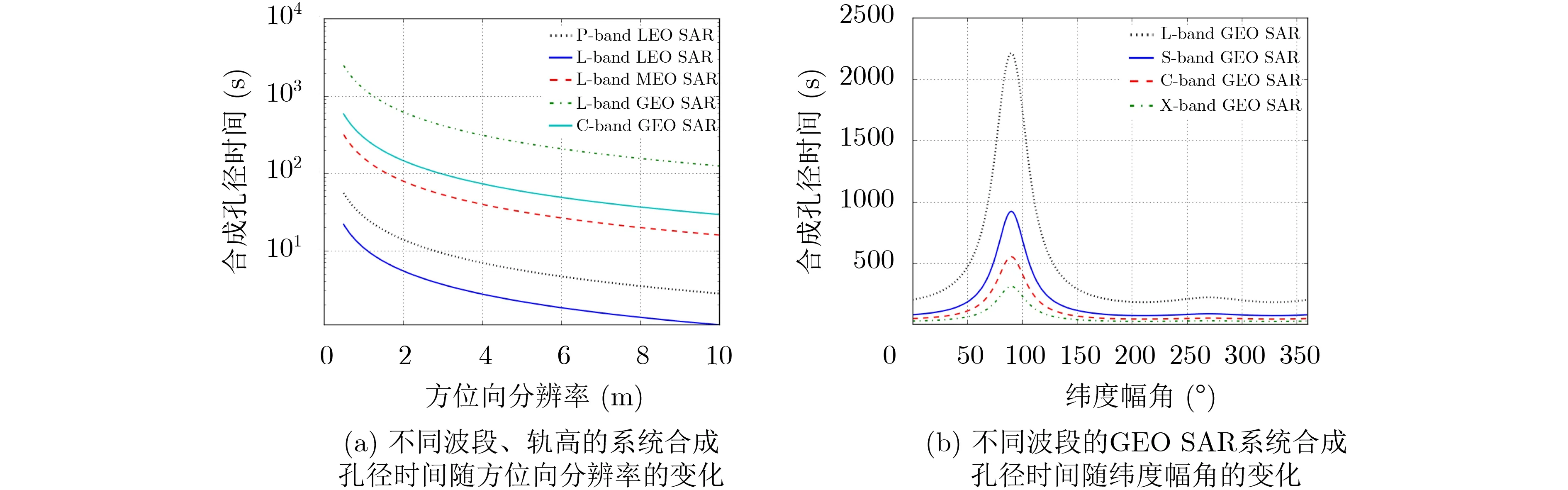
图4 合成孔径时间的计算

4.2 STEC各阶系数容限

接下来，考察不同星载SAR系统对时变STEC各阶系数的容忍度。通常认为，当偏移量小于一个分辨单元时，就可以忽略偏移的影响；另外，当2次相位误差小于45°以及3次相位误差小于22.5°，就可以忽略成像性能的恶化。故这里令|ΔLa|=ρa,QPEa=45°,C PEa=22.5°，分别计算不同中心频率、合成孔径时间情况下的时变STEC各阶系数容限，结果如图5所示。可见，中心频率越低、合成孔径时间越长，对应的|k1|,|k2|,|k3|容限越小，则意味着系统方位向成像越容易受到时变STEC的影响。

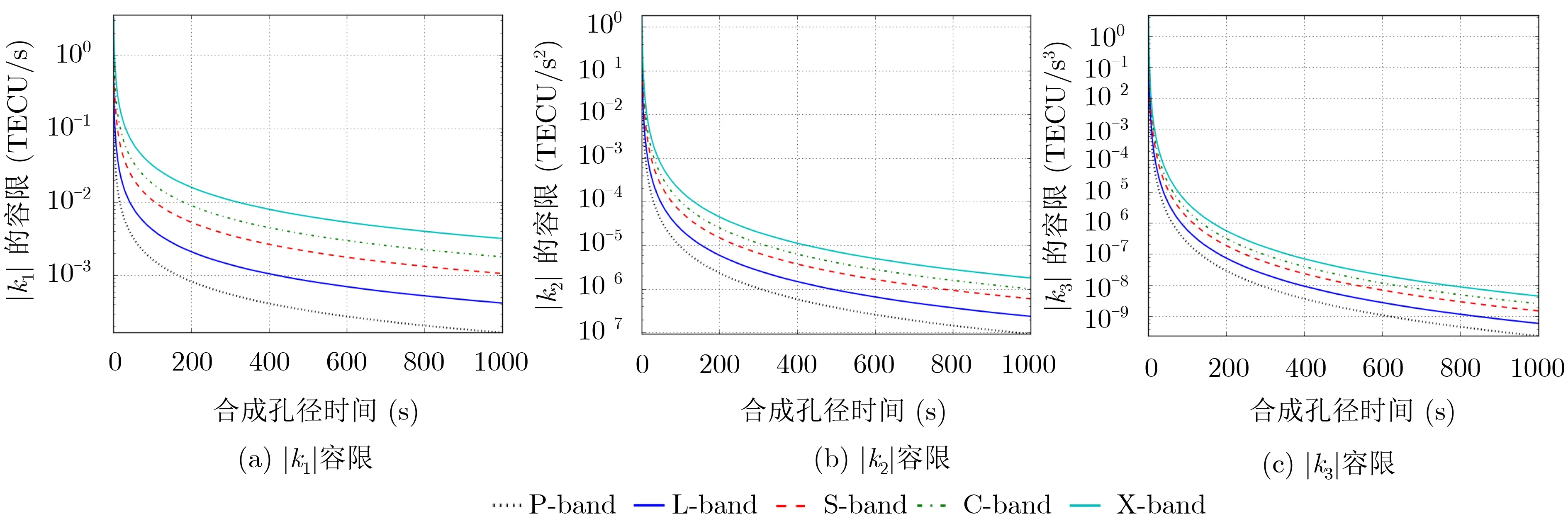
图5 时变STEC各阶分量系数的容限曲线

表1给出了不同星载SAR系统的时变STEC各阶系数容限值，下面的分析需要对照上节中的结论。对于表中所列举的两种P波段LEO SAR系统，时空变VTEC对应的都可能会超过|k1|容限，从而导致超过一个方位分辨单元的方位偏移；而传播路径变化引起的可能会导致方位向散焦。对于PALSAR-2聚束模式，在较大的情况下，同样需要考虑空变VTEC和传播路径变化的影响。对于L波段MEO SAR，仅需考虑时变VTEC引入的方位向偏移。而对于L波段GEO SAR，时变VTEC可造成显著的方位向偏移和散焦，而空变VTEC以及传播路径变化的影响基本可以忽略。

5 信号仿真

本节进一步探讨时空变背景电离层对不同星载SAR方位向成像性能的影响，这里主要涉及表1中的6种系统。首先，利用图1中2001年12月15日海口地区的实测VTEC时变数据，取当地时间9时为中心时刻，时间跨度为不同系统对应的合成孔径时间；另外，背景电离层穿刺点路径上的∇VTEC设置为0.01 TECU/km。结合不同系统，表2给出了各因素导致的时变STEC各阶系数值。对于LEO SAR系统，k1,k2分别主要来源于；对于MEO SAR系统，3种因素对k1,k2,k3的贡献几乎在同一量级；而对于GEO SAR系统，k1,k2,k3分别主要来源于。

表1 不同星载SAR系统对应的时变STEC各阶系数容限

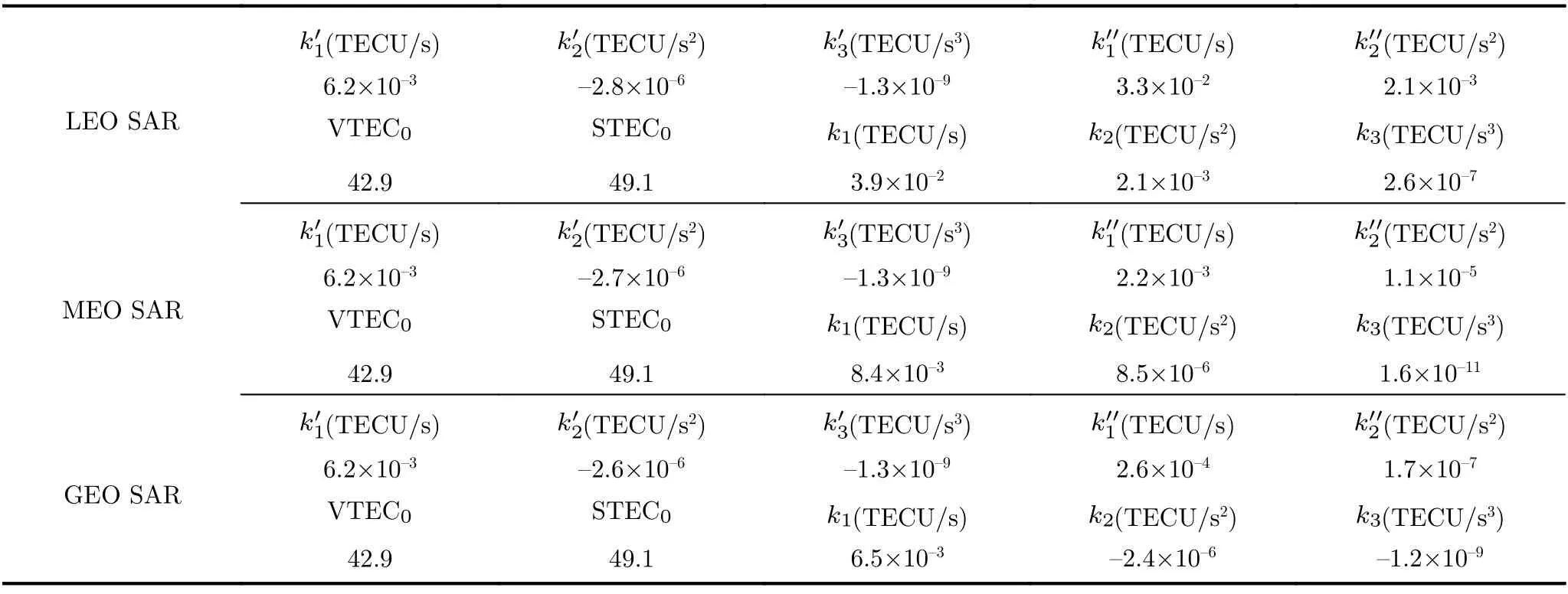
表2 仿真中各因素导致的时变STEC各阶系数值

图6给出了时变STEC影响下不同星载SAR点目标图像的方位向剖面，表3列出了不同系统对应的方位向成像性能指标。对于P波段LEO SAR，理论方位偏移值为6.65 m,5 m,2 m的方位分辨率对应的方位向QPE分别为32.40°,202.09°；对于PALSAR-2，理论方位偏移值为1.03 m，QPE为50.19°；对于L波段MEO SAR聚束模式，理论方位偏移值为3.22 m，QPE为9.20°；对于L波段GEO SAR，理论方位偏移值为19.8 m，200 s,600 s的合成孔径时间对应的方位向Q P E 分别为1 8.6°,167.0°，方位向CPE分别为0.9°,25.1°。进一步与仿真结果相对照，其中5 m分辨率P波段LEO SAR、L波段MEO SAR以及200 s合成孔径时间的L波段GEO SAR方位向聚焦性能保持得比较好。而2 m分辨率P波段LEO SAR,PALSAR-2以及600 s合成孔径时间的L 波段GEO SAR出现了较为严重的方位向散焦，主要表现为主瓣展宽、旁瓣抬升和峰值能量损失，且图6(f)中出现了明显的高低旁瓣，主要是由于方位向CPE超过了容限值。另外，方位偏移与理论计算值基本一致，进一步验证了理论分析模型的有效性。

图6 时变STEC各阶分量系数的容限曲线

表3 不同星载SAR系统对应的时变STEC各阶系数容限

因此，对于低波段LEO SAR，空变VTEC和传播路径变化是导致时变STEC的主要因素，前者将引入方位向偏移，后者可导致明显的方位主瓣展宽，特别是对于方位分辨率为2 m的星载P波段SAR系统和PALSAR-2聚束模式。对于L波段MEO SAR，方位成像性能的恶化可忽略不计，但VTEC的时空变效应导致的方位向偏移不可忽略。对于L波段GEO SAR，时变VTEC成为导致时变STEC的主要因素，可造成明显的方位向偏移、主瓣展宽、旁瓣抬升以及高低旁瓣现象。

6 结束语

时-空变化的背景电离层将会导致方位时变的STEC，从而对星载SAR方位向成像造成影响。方位时变STEC对星载SAR方位向成像的影响可以归结于3个具体因素：背景电离层VTEC的时间和空间变化，以及传播路径变化。对于低波段LEO SAR，由于合成孔径时间短，空变VTEC和传播路径变化是导致时变STEC的主要因素，将分别引入方位向偏移误差和二次相位误差；随着轨道升高，合成孔径时间增加，时变VTEC逐渐成为导致时变STEC的主要因素，将会导致方位向图像偏移和散焦。

在给定的背景电离层条件下，不同的星载SAR系统由于主导因素不同，因此其方位向成像性能呈现出不同程度的恶化。例如，对于设计方位分辨率为2 m的星载P波段LEO SAR系统，时空变背景电离层引入了6.65 m的方位向偏移误差以及超过200°的2次相位误差，方位向剖面严重散焦；而对于600 s合成孔径时间的L波段GEO SAR系统，时空变背景电离层引入了19.8 m的方位向偏移误差、167.0°的2次相位误差以及25.1°的3次相位误差，方位向散焦严重且出现了明显的高低旁瓣。总之，随着星载SAR载频的下降、设计方位分辨率的提高、合成孔径时间的增大，时空变背景电离层将会导致更加严重的方位向偏移与图像散焦，因此必须在系统设计以及后端信号处理环节加以考虑。