基于非整数阶SSC盲移频的LFM雷达干扰技术

赵忠凯 周文彬 李 虎

①(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

②(试验物理与计算数学国家级重点实验室 北京 100876)

1 引言

线性调频信号(Linear Frequency Modulation,LFM)较好地解决了探测距离和距离分辨率二者之间的矛盾，在脉冲压缩体制雷达中得到了广泛应用，引发了许多学者对该类雷达干扰技术的大量研究[1]。数字射频存储(Digital Radio Frequency Memory,DRFM)技术能够快速准确地存储接收到的雷达信号，并利用采集到的雷达信号产生相参干扰信号，已经成为一种重要的雷达干扰手段[2]。移频干扰的原理是利用DRFM技术将时变相位添加到已截获雷达信号的相位中。根据匹配滤波器的特性，增加的相位将导致假目标滞后或者超前于真实目标。移频干扰产生了单个欺骗假目标，然而单个欺骗假目标的干扰效果有限，在此基础上文献[3–5]提出了导前假目标群干扰，将移频干扰和间歇采样相结合，实现了超前的间歇采样假目标群干扰，具有更好的干扰效果。随着雷达抗干扰技术的发展，文献[6–9]提出了一种调频斜率捷变的雷达，其信号的调频斜率在脉间变化，导致传统的移频干扰失去干扰效果。为应对这种雷达以及隐藏干扰特征参数，文献[10,11]提出一种N阶频谱扩展—压缩(Spectrum Spread and Compression,SSC)的方法，通过采用该技术，可产生固定位置的假目标干扰信号，能够很好地应对捷变频雷达。但是这种传统SSC盲移频干扰的系统阶数N为整数，需要调节干扰机处理延时来实现特定精确位置的干扰，具有一定的局限性。

针对传统SSC盲移频干扰的应用局限性，本文提出了一种基于非整数阶SSC盲移频干扰算法。首先对SSC盲移频干扰算法原理进行了介绍；其次，对非整数阶SSC盲移频干扰算法进行了推导，得到了欺骗干扰和压制干扰的高效实现框图；然后，针对SSC盲移频压制干扰峰均比(Peak-to-Average Power Ratio,PAPR)过高的问题，应用Newman序列对信号初相进行控制，抑制干扰信号的峰均比；文章最后进行了仿真试验，验证了所提算法的有效性。

2 N阶SSC盲移频干扰算法

移频干扰是对抗脉冲压缩雷达的一种有效手段，其利用DRFM技术截取并存储雷达信号，通过对截取到的信号进行处理，附加一个移频量，从而产生了移频干扰假目标。

假设截取的雷达线性调频信号的表达式为

附加移频量为Δf，得到干扰信号的表达式为

其中，调频斜率μ=B/T，B为谱宽，T为时宽，f0为载频。函数rect的表达式为

可以得到干扰距离为

但是当雷达的调频斜率改变时，由于干扰方不能实时测得调频斜率的变化，干扰距离会发生变化，从而被雷达识别出来失去干扰效果。为了应对捷变频雷达，可以采用SSC盲移频干扰。SSC盲移频干扰的原理是：通过对采样到的LFM雷达信号及其延时信号做N阶和N-1阶频谱扩展，并利用后者对前者进行脉冲压缩，能够产生固定位置的假目标[10,11]。由于其不需要测得雷达信号的谱宽、时宽以及调频斜率，因此能够很好地应对调频斜率捷变的雷达。具体的干扰处理框图如图1所示。

图1 SSC盲移频干扰处理框图

假设线性调频信号的N次方为

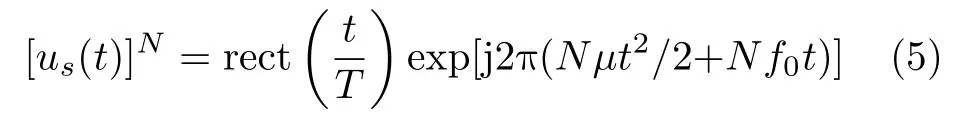
然后对原始信号的延时共轭进行(N–1)阶频谱扩展，可得

将式(5)和式(6)两个信号相乘即可得到N阶盲移频干扰信号为

由式(8)可以得出欺骗距离ΔR

通过式(10)可以看出，干扰假目标的欺骗距离仅与系统参数N和干扰机处理延时τ有关。既使雷达信号的中心频率、带宽或者脉宽发生了改变，假目标和真实目标之间的距离也不会发生改变。因此，整数阶SSC盲移频干扰信号能够隐藏特征参数，从而很好地应对调频斜率捷变的雷达。

3 非整数阶SSC盲移频干扰

3.1 非整数阶SSC欺骗干扰

整数阶SSC盲移频干扰信号能够很好地应对捷变频雷达，但是其要求系统阶数为整数，想要获得不同欺骗距离的假目标，需要改变干扰机的处理延时，具有一定的应用局限性。为了能够控制干扰机的处理延时不变，本文提出了一种非整数阶的SSC盲移频干扰算法，即设定一个合适的干扰机处理延时，通过改变系统阶数来达到精确控制假目标位置的目的，系统阶数为任意的实数。

当N为非整数时，在生成SSC盲移频信号过程中需要对截取的雷达信号做N阶和N–1阶频谱扩展。由De Moivre定理，复数的非整数次幂表达式

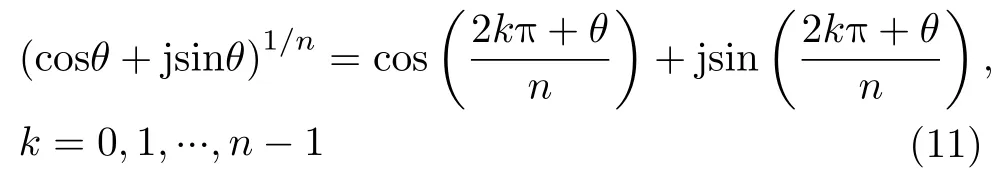
由式(11)可知，一个复数的非整数次幂有多个不同的解，若求信号us(t)的非整数次幂，得到的信号[us(t)]N的表达式

由于N为非整数，则2πkN不是2 π的整数倍，信号[us(t)]N不连续。为了对信号us(t)做非整数阶频谱扩展且保证信号[us(t)]N的连续，可以对截获信号us(t)的 相位函数进行处理。取常数k=0可以得到

具体的处理框图如图2所示。首先提取雷达信号的相位函数，并对相位函数及其延时放大N倍和N–1倍，然后进行运算处理得到干扰信号的相位函数，最后还原得到非整数阶SSC盲移频干扰信号。

图2 非整数阶SSC盲移频干扰处理框图

截获雷达信号并利用DRFM技术将其存储，分别对信号及其延时信号进行N阶和(N–1)阶频谱扩展，可得

其相位函数为

将计算得到的相位函数还原成干扰信号

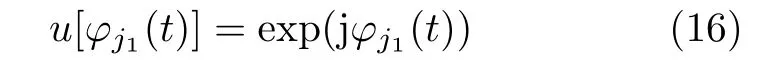
对其做匹配滤波，匹配滤波的表达式为

匹配滤波器的输出为

把Δf=μ(N-1)τ代入式(18)中得到

由 sinc 函数的性质可知，当t=-(N-1)τ时输出最大峰值，此时t始终落在第1个取值区间。从而可以得到匹配滤波增益为

假目标与真实目标的距离差为

由式(19)、式(20)可得，非整数阶SSC的匹配滤波增益和干扰距离由系统参数N和干扰机处理延时τ决定，Nτ的值越小，匹配滤波增益越高，假目标与真实目标的距离差越小。

3.2 非整数阶SSC压制干扰

非整数阶SSC欺骗干扰可以产生特定精确位置的假目标，但是其生成的单个假目标对雷达的干扰效果有限，因为大多数雷达同时具备搜索和跟踪功能，即使雷达把假目标误认成真实目标并进行跟踪，雷达仍然可以检测并跟踪真实目标[12]。除了可以跟踪多个目标，雷达还可以采用副瓣匿影技术去除从副瓣进入的假目标，假目标数量太少很容易被去除从而失去干扰效果。而由相参密集假目标生成的压制干扰，即使雷达使用了副瓣匿影技术也无法完全去除密集假目标，而且密集的假目标信号可以使得雷达信号处理饱和，无法跟踪到真实目标。因此本文将多个SSC盲移频干扰信号叠加，从而生成干扰效果更好的压制干扰。其方法是将3.1节中生成的单个SSC干扰信号线性相加，处理框图如图3所示。

图3 SSC压制干扰处理框图

由式(13)—式(16)可以得到非整数阶SSC压制干扰信号为

3.3 压制干扰峰均比抑制

在生成非整数阶SSC压制干扰信号时，每间隔一个符号周期，信号会出现一个尖峰。这是由于SSC压制干扰信号是由多个独立的SSC干扰信号累加形成的。因此当这些信号的初相相同或相近时，所获得的压制信号的瞬时功率比信号的平均功率高很多，将导致所生成的压制干扰信号具有较高的峰均比。干扰系统的主要考虑因素是干扰输出功率，如果SSC压制干扰信号的峰均比较高，就会严重影响信号的干扰输出功率[13]。

鉴于SSC压制干扰信号高峰均比的问题，从技术可行性的角度出发，拟采用一种较新的降低SSC压制干扰信号PAPR的优化方案，使其在降低PAPR和提高系统功率放大器的功率效率的同时保证信号不发生畸变。降低峰均比的方法大致分为两类：线性和非线性。非线性的方法复杂度低，可以快速降低峰均比，但是会造成信号的失真。因此我们采用线性的方法来降低峰均比，常用的方法是在信号的相位上加上某个合适的序列[14–16]。

根据峰均比的定义，PAPR是指信号的峰值功率和该信号的平均功率的比值。在1个符号周期T内的PAPR定义为

可以看出，为了使合成信号的幅度最小，可以优化给定时间范围内包络函数的N个初相组合函数，这样可以减小SSC叠加信号的峰均值功率比。

最常用的初相序列有随机初相序列和Newman初相序列。随机初相序列是给相位函数加上一串随机相位序列，从而使密集假目标信号的初相序列不同；Newman初相序列由D.J.Newman提出，与式(24)的最小近似二次解相对应。Newman初相序列的优化近似公式为

4 仿真分析

4.1 非整数阶SSC欺骗干扰仿真

假设截获的雷达信号为线性调频信号，雷达信号脉宽T为100 μs，带宽B为10 MHz，信噪比为20 dB，雷达距离真实目标100 km。采样频率fs为100 MHz，为了得到欺骗距离为1.5 km的假目标，取常规移频干扰的移频量为1 MHz，盲移频干扰的系统阶数N为3.5，干扰机处理延时4 μs，分别生成常规移频干扰和SSC盲移频干扰信号后，做匹配滤波得到的脉冲压缩信号如图4(a)所示。当雷达信号的带宽变为20 MHz时，调频斜率变为原来的两倍，保持干扰信号参数不变，通过匹配滤波器后的仿真结果如图4(b)所示。

图4中，干扰1代表非整数阶SSC盲移频干扰信号，干扰2代表常规移频干扰信号。对比图4(a)和图4(b)可以看出，随着调频斜率k的改变，由于不能根据调频斜率实时改变移频量，常规移频干扰的位置发生了跳变，从而得不到脉冲累计容易被识别出来，失去干扰效果。非整数阶SSC盲移频干扰的假目标位置保持不变，对雷达具有干扰效果。

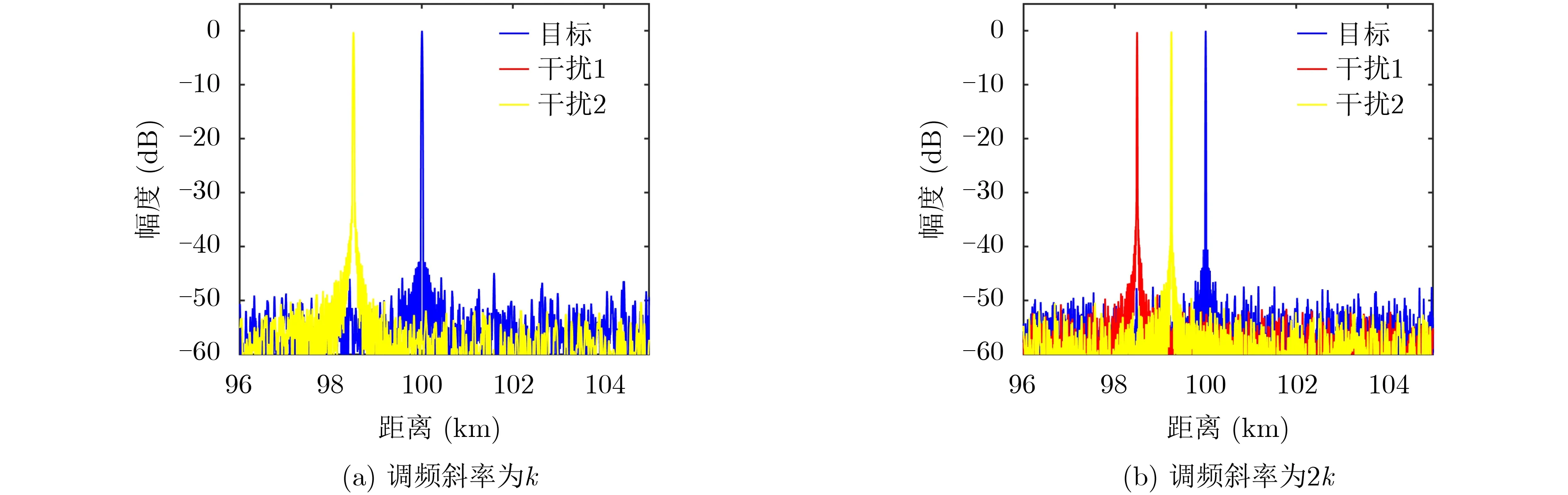
图4 不同调频斜率下的脉冲压缩图

然后对非整数阶SSC盲移频干扰的脉冲压缩增益进行分析。假设截取相同的雷达信号，设定干扰机的处理延时保持不变，选取系统阶数N的值分别为3.5和5.5，生成SSC盲移频干扰信号后做匹配滤波，仿真结果如图5所示。

在图5中，干扰1代表N为3.5时的干扰信号，干扰2代表N为5.5时的干扰信号。可以看出，在干扰机处理延时不变的情况下，改变系统阶数N的值可以实现特定位置的欺骗干扰，且随着N的增大，欺骗距离越来越大。在N为3.5和5.5时，干扰1和干扰2分别超前目标1.5 km和2.7 km。但当欺骗距离增大时，脉冲压缩增益有所减小。

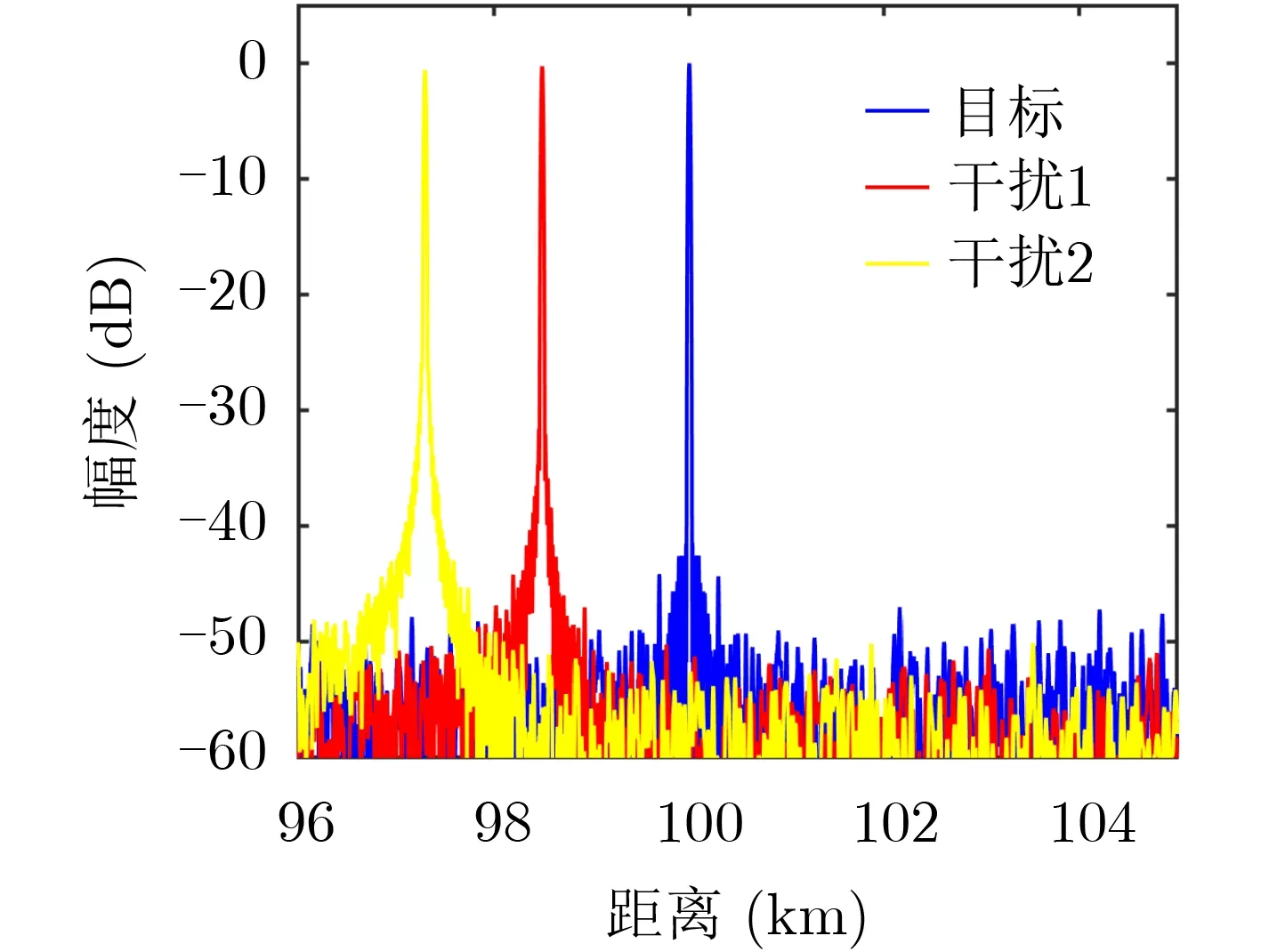
图5 不同N值的脉压图

非整数阶SSC盲移频干扰具有与整数阶SSC盲移频干扰相同的优点，其欺骗假目标的位置与调频斜率无关，能够很好地应对调频斜率捷变的雷达。脉冲压缩增益与阶数N和干扰机处理延时的乘积有关，乘积越大，欺骗距离越大，脉冲压缩增益越小。然而在生成特定位置的欺骗假目标时，整数阶SSC盲移频干扰为了保证阶数N为整数，需要调节干扰机处理延时来生成欺骗假目标；非整数阶SSC盲移频干扰则可以控制干扰机处理延时不变，调节阶数N的值即可生成欺骗假目标，在实际应用中更容易实现。

4.2 非整数阶SSC压制干扰仿真

对非整数阶SSC压制干扰进行仿真验证，假设截获的雷达信号参数保持不变。设定干扰机处理延时为4 μs，SSC盲移频干扰的系统阶数N在3～5范围内均匀取样16个点，可以得到16个密集的假目标，最后将生成的干扰信号叠加。生成两种压制干扰，一种使初相为零，一种加入Newman相位，得到如图6所示的压制干扰信号时域图。

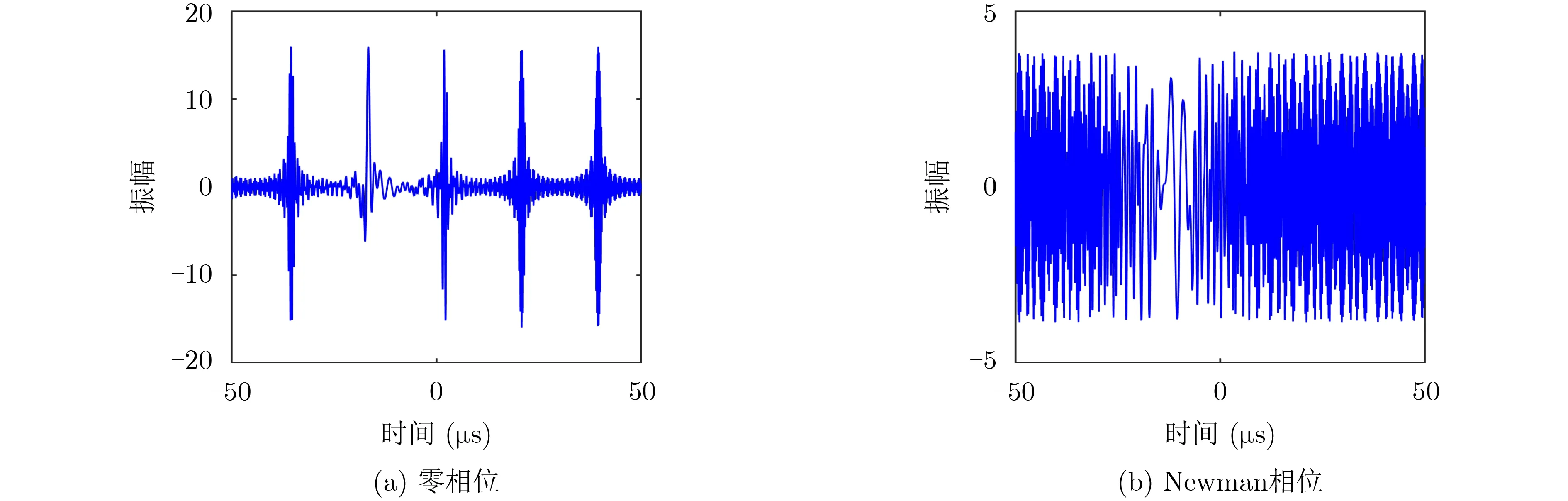
图6 压制干扰时域图

图6(a)是初相为零的信号时域图，其幅度峰值很高，说明峰均比很大；而图6(b)是加入Newman相位后的信号，其时域信号无明显峰值，且信号包络幅度变化不大，说明采用Newman相位后，压制干扰信号的峰均比得到了明显的改善。

将上述加入Newman相位后的SSC盲移频叠加干扰信号通过匹配滤波器，得到的脉冲压缩干扰信号如图7所示。

图7是加入Newman相位后，非整数阶SSC压制干扰脉冲压缩图。通过观察可以看出，多个非整数阶SSC盲移频干扰信号叠加可以形成密集的压制干扰。压制干扰距离真实目标的范围在1.2～2.4 km，且压制干扰的位置和压制范围不会随雷达调频斜率的变化而发生改变。非整数阶SSC盲移频干扰不仅具有整数阶SSC盲移频干扰的欺骗效果，而且还能对雷达产生很好地压制效果。

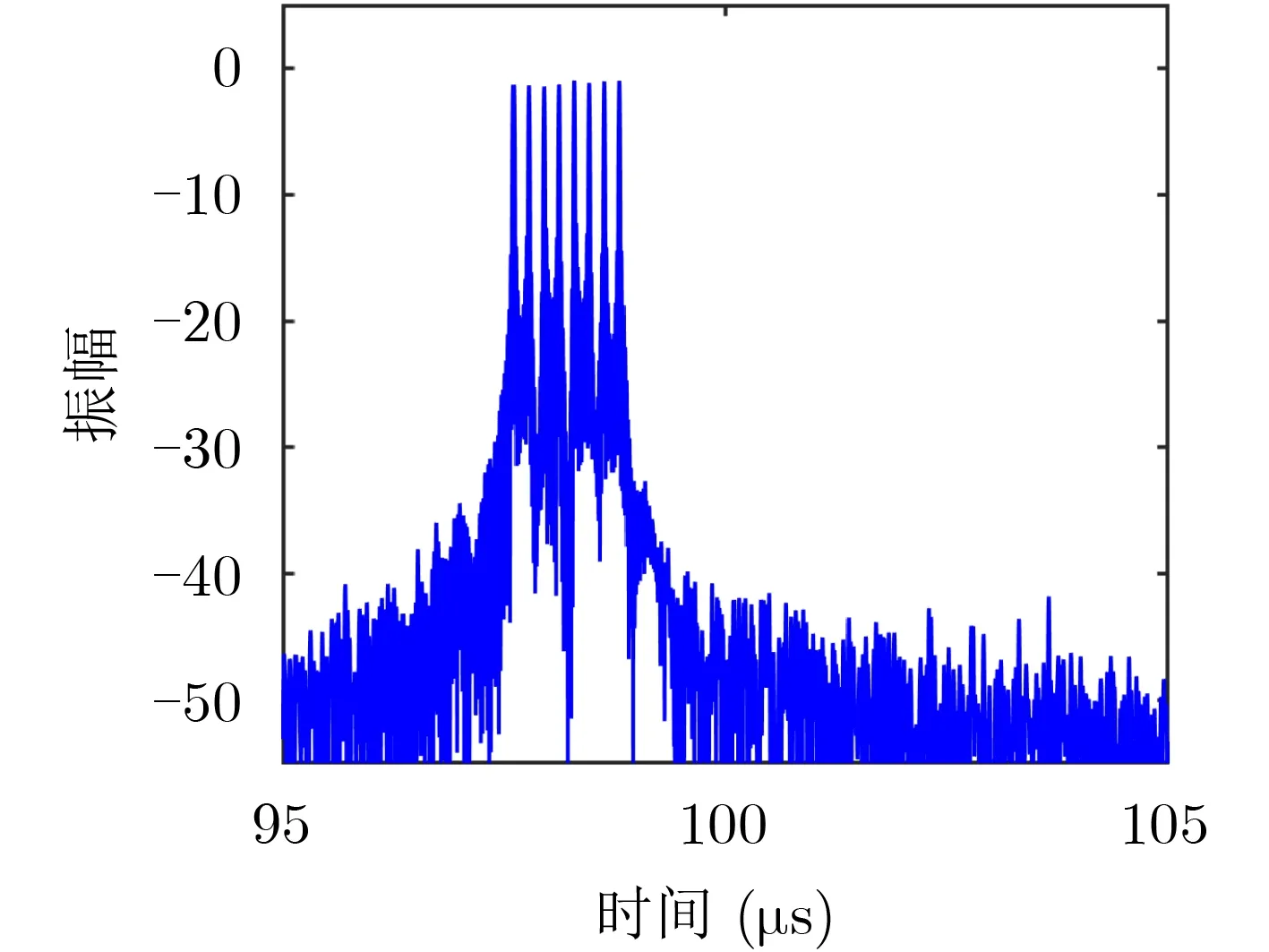
图7 压制干扰脉压图

4.3 降低峰均比的方法比较

假设截获的雷达信号参数保持不变，设定干扰机处理延时为4 μs，系统阶数N在3～5范围内均匀取样，分别取样8,16和32点，采用SSC盲移频技术生成压制干扰信号。分别计算并比较初相为0、随机相位和Newman相位的干扰信号的PAPR值，仿真结果如表1所示。

表1 在3种不同相位情况下的PAPR值(dB)

从表1可以看出，加入随机相位和Newman相位后的PAPR值要明显低于初相为0的PAPR值。采用随机相位后的PAPR值比采用Newman相位的PAPR值大，是因为其加入的相位是随机改变的，所以降低峰均比的效果欠佳，一般不采用；而采用Newman相位后，信号的PAPR值更加稳定，且减小的幅度很大，是比较好的选择。因此我们可以给SSC压制干扰信号加入Newman相位以降低信号峰均比，从而提高干扰机能量利用率。加入相位会给干扰信号带来微小的移频量，但是加入的相位θn ≪Δfθn ＜＜Δf，带来的误差可以忽略不记。

5 结束语

本文在传统SSC盲移频干扰的基础上，提出了一种非整数阶SSC盲移频干扰技术。该技术通过固定干扰机处理延时不变，采用不同的系统阶数来生成特定位置的雷达假目标干扰信号。文章首先推导了非整数SSC盲移频干扰的处理框图，得到了基于CORDIC和乘加运算的高效实现结构；其次针对压制干扰信号高峰均比问题，通过加入Newman序列大幅度降低峰均比；最后通过仿真实验验证了该算法在特定的干扰处理延时情况下，能够生成假目标欺骗干扰和相参密集压制干扰。文章所提方法解决了传统SSC盲移频干扰的系统阶数必须为整数的问题，能够有效对抗脉冲压缩体制雷达，具有较好的工程应用价值。