基于TFM-PBM耦合模型的离心泵内微气泡破碎合并的模拟研究
2021-10-31高颂徐燕燕李继香叶爽黄伟光
高颂,徐燕燕,3,李继香,叶爽,黄伟光,3
(1中国科学院上海高等研究院,上海 201210;2中国科学院大学,北京 100049;3上海科技大学物质科学与技术学院,上海 201210)
引 言
微气泡因其液中存在时间长、吸附效率高、破碎瞬间释放大量自由基等特点[1],能有效吸附分离液相中的固体颗粒、提高化学反应速率,被广泛应用于工业废水废气处理[2-4]。研究表明污染物去除率与气泡尺寸、气泡数密度相关,而工业大量制备微气泡常采用离心泵,由于泵内气泡流动极其复杂,目前离心泵产生的气泡尺寸较大且不够均匀,其微气泡发生性能亟待优化[5]。因此,探究泵内气泡破碎合并机理,揭示离心泵内微气泡尺寸变化规律具有研究价值。
多相流体系中分散相的粒度分布常采用群体平衡模型(PBM)来描述,其本质是对不同粒度的分散相分别建立质量守恒方程。Hulburt等[6]首次运用该思想结合矩量法对化工过程中固体颗粒的粒度变化建立平衡方程。Kuboi等[7-8]采用高速摄影研究了液相旋转流场中液滴的运动,发现两个液滴碰撞后的合并分数由碰撞瞬间的动能决定。Coulaloglou等[9]受Kuboi等的启发,将Hulburt等建立的群体平衡方程拓展到旋转流场液液两相中液滴的破碎合并,并首次提出破碎合并函数。Lee等[10]进一步将群体平衡模型拓展到气液两相中气泡的破碎合并,并用气泡的数密度代替气泡的概率密度分布。Prince等[11]考虑由于密度差异引起碰撞频率、破碎效率的改变,对合并函数、破碎函数进行修正。上述群体平衡模型仅提供总体破碎率,且模型包含需实验测定的未知参数,通用性不高。Luo等[12-13]研究发现气液两相中气泡间的碰撞主要由湍流涡随机运动导致,进而将碰撞频率的计算模型进行了简化,同时参考Kuboi等的研究将能谱与涡能量结合,提出同一尺寸湍流涡的能量服从指数分布,用来流涡的湍动能大于气泡一分为二时表面能的增量作为液滴发生破碎的衡量标准,建立破碎模型,该模型无未知量且破碎后的子气泡尺寸呈U形分布,与实际情况较为吻合。Luo等的群体平衡模型虽可以直接预测气泡破碎合并,但模型中包含流场参数,对泵内流动需先获得基础流场才能求解气泡尺寸分布。
Murakami等[14-16]通过对旋转流场的孤立气泡求解气泡运动方程,发现相间作用力由曳力、虚拟质量力、升力主导,其中曳力影响最大,还指出沿泵内流动方向压力由负向正转变,大气泡流速先增加后减小会在叶轮内产生聚集。Patel等[17]观察到叶轮入口区域小气泡发生聚集,验证了前人研究。Falcimaigne[18]通过可视化研究了在入口气含率(IGVF)为10%的条件下,螺旋轴泵中气泡直径的范围,为气泡尺寸离散打下基础。Kumar等[19]通过气泡尺寸离散改良了已有的群体平衡方程求解方法,使其可以与计算流体力学(CFD)耦合求解。Lehr等[20]将双流体模型(TFM)与群体平衡模型(PBM)耦合用于鼓泡床气液两相上升流场的求解,以获得气泡尺寸分布。Venneker等[21]将TFM-PBM用于求解搅拌釜中的气液两相旋转流场,以研究气泡尺寸分布与体积传质系数。Zhu等[22]发现使用瞬态Euler-Euler的TFM耦合PBM,较使用VOF(volume of fluid)模型耦合PBM能更好地预测离心泵内部两相分布。He等[23]、Ge等[24]通过实验与数值模拟验证了这一点,其研究还表明Realizablek-ε湍流模型与Luo等的破碎合并模型在离心泵仿真中能较好地修正扬程计算。尽管TFM-PBM耦合模型能求解气泡尺寸分布,但目前用于离心泵的数值研究大多仅关注其对扬程、相分布的修正结果,对整个泵内的气泡尺寸沿程变化受运行参数的影响规律仍有待研究。与此同时,研究者[22-24]大多使用Luo等基于湍流涡能量提出气泡破碎合并模型,但在分析仿真结果时却鲜有提及其影响。
本文为探究离心泵内微气泡的尺寸变化规律,采用文献[25]可视化研究的离心泵模型,以TFM为基础,对两相旋转流场中的质量守恒、动量守恒建模,用以求解基础流场;同时考虑相间作用力对相间动量传递的影响,用以修正动量守恒;并耦合PBM求解气泡粒度分布,用以修正气泡破碎合并对相间作用力的影响;最后用已有的可视化研究成果对仿真效果进行验证。在此基础上,结合Luo等的模型分析,气含率、湍流耗散率、气泡尺寸会影响气泡的破碎合并,应用TFM-PBM分别模拟模型泵在不同IGVF、不同入口气泡尺寸下的内部流动,通过逐层分析气含率、气泡尺寸对气泡在叶轮、蜗壳内尺寸变化的影响机理,揭示其对出口气泡尺寸的影响规律,为提高基于旋转流场的微气泡发生效果提供参考。
1 数学模型
1.1 双流体模型
离心泵内的气液两相旋转流场符合连续介质假设,本文采用Ishii等[26]在此基础上构造的双流体模型求解基础流场,考虑到空气-水两相在泵内流动温度变化不大,忽略能量守恒方程。
1.1.1 质量守恒方程 常温下空气-水体系的传质对流动影响较小,张振铎[25]的研究表明入口压力高于40 kPa时,模型泵内无空化发生,可忽略气液两相的传质。后续仿真保证该条件,则有:
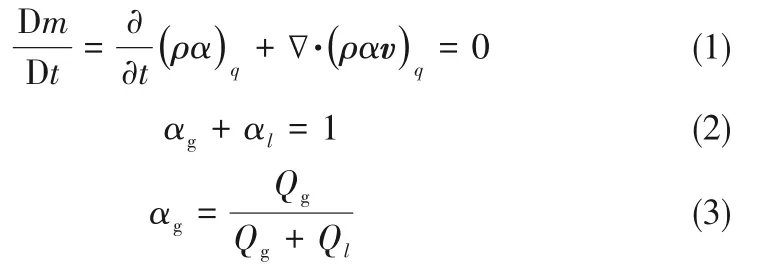
式中,t为时间,s;m为质量,kg;ρ为密度,kg/m³;v为速度,m/s;α为体积相含率;q用于区分相,q=l为液相,q=g为气相;Q为体积流量,m³/s。
1.1.2 动量守恒方程
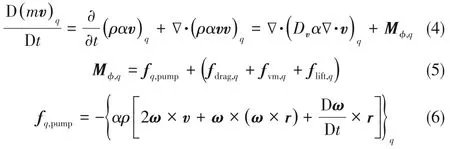
式中,fq,pump为叶轮旋转作用力,N;fdrag,q、fvm,q、flift,q分别为曳力、虚拟质量力、升力,N;r为单位控制体到旋转中心的矢量;ω为非惯性系的旋转角速度,rad/s。
1.2 相间作用力模型
1.2.1 曳力 离心泵内空气-水两相密度与黏度差异会引起两相在外力共同作用下运动时存在速度滑移,低速相流体会阻碍高速相流体的运动,即曳力。Ge等[24]的研究表明Schiller and Naumann曳力模型能较好修正离心泵在IGVF<5%时的扬程计算,本文采用该模型求解IGVF<5%时气泡所受的曳力:
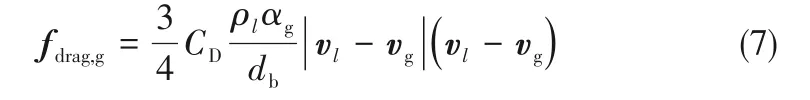
式中,db为气泡的Sauter平均直径,m;曳力系数CD计算如下:
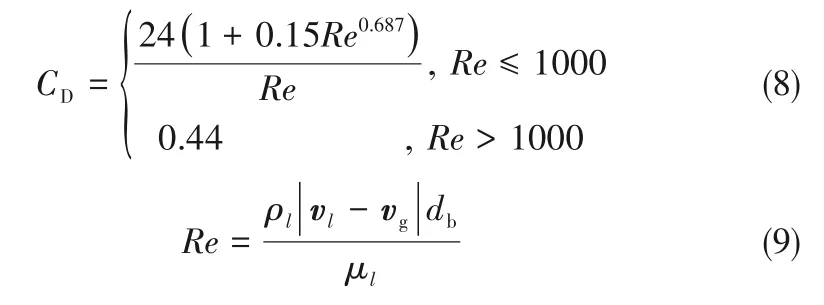
式中,Re为连续相相对分散相的相对Reynolds数,表征两相速度差异;μl为液相的动力黏度,N·s/㎡。
1.2.2 虚拟质量力 离心泵内的空气-水两相密度差会引起加速度差异,进而在相界面形成挤压力,即虚拟质量力。由于ρg≪ρl,该力不可忽略,本文采用Maxey等[27]构造的势流中球形颗粒的虚拟质量力模型:
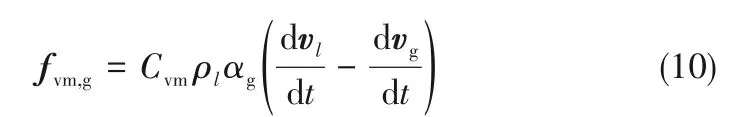
式中,虚拟质量力系数Cvm=0.5。
1.2.3 升力 离心泵内流场存在一个垂直于气泡流线方向的压力梯度,即升力。本文采用Legendre等[28]提出的适用于小直径球形流体颗粒的升力模型:
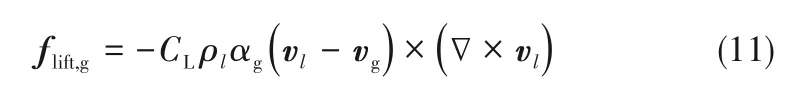
式中,CL为升力系数。
1.3 湍流模型
由于湍流脉动的随机性,相同条件下流场上的同一点的同一物理量在同一瞬时存在不同的值,为获得更有普遍意义的平均值,Thomas等[29]通过推导、简化,并综合考虑线变形与角变形对涡黏系数进行修正,获得适用于旋转流场动量守恒方程求解的k与ε的输运方程(即Realizablek-ε湍流模型),戈振国[30]验证了该模型在旋转流场IGVF<5%时的适用性,本文采用该模型求解动量守恒方程。
1.4 群体平衡模型
1.4.1 气泡群体平衡模型 离心泵内气泡的破碎合并现象满足气相质量守恒,且泵内流场满足各向同性假设,同时假定泵内气泡仅发生一分为二的破碎,则可采用Luo等[12-13]的群体平衡模型进行描述:
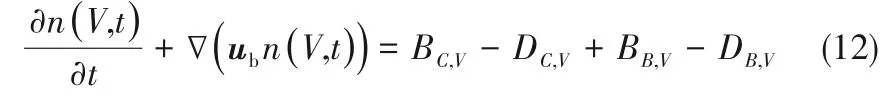
式中,n(V,t)为t时刻单位体积内体积为V到V+dV的气泡个数,1/m³;ub为气泡速度,m/s。
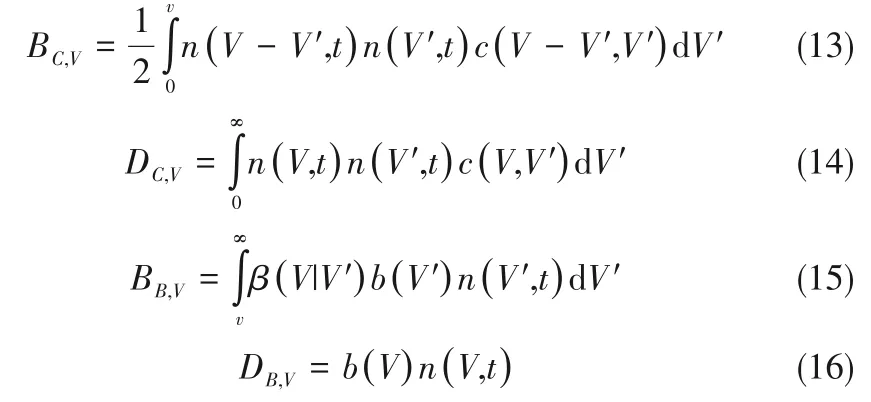
式中,BC,V为气泡V'与气泡V-V'合并生成气泡V的源项;DC,V为气泡V与气泡V'合并导致气泡V消失的源项;BB,V为气泡V'破碎生成气泡V的源项;DB,V为气泡V破碎导致气泡V消失的源项;c(VV',V')为气泡V'与气泡V-V'合并生成气泡V的合并概率,1/(m3·s);b(V')为气泡V'的破碎概率,1/(m3·s);β(V|V')为气泡V'破碎后生成气泡V的概率。合并概率、破碎概率由相应的模型来描述。
1.4.2 气泡破碎模型 基于上述分析,本文采用Luo等[12-13]的破碎模型。该模型将气泡破碎拆解为两个过程,即首先需要气泡与湍流涡碰撞,当碰撞时湍流涡的能量满足一定条件才会引起破碎。并基于搅拌器内实验数据进一步假设尺寸为λ的湍流涡的能量分布服从指数分布,将碰撞时湍流涡的能量能否引起破碎分解为三个层次进行建模。为区分气泡的不同破碎方式,假设气泡发生破碎后仅生成两个子气泡,fBV破碎为其中一个子气泡的体积与原气泡的体积之比为fBV。模型用PB(d,fBV,λ)表示来流涡尺寸为λ时,其能量可以使气泡发生fBV破碎的概率;用PB(d,fBV)代表在可使气泡发生fBV破碎的湍流涡尺寸范围[λmin,d]内,气泡V'发生fBV破碎的频率;用PB(d)代表在可使气泡发生fBV破碎的湍流涡尺寸范围[λmin,d]内,气泡V'发生任意破碎的频率。
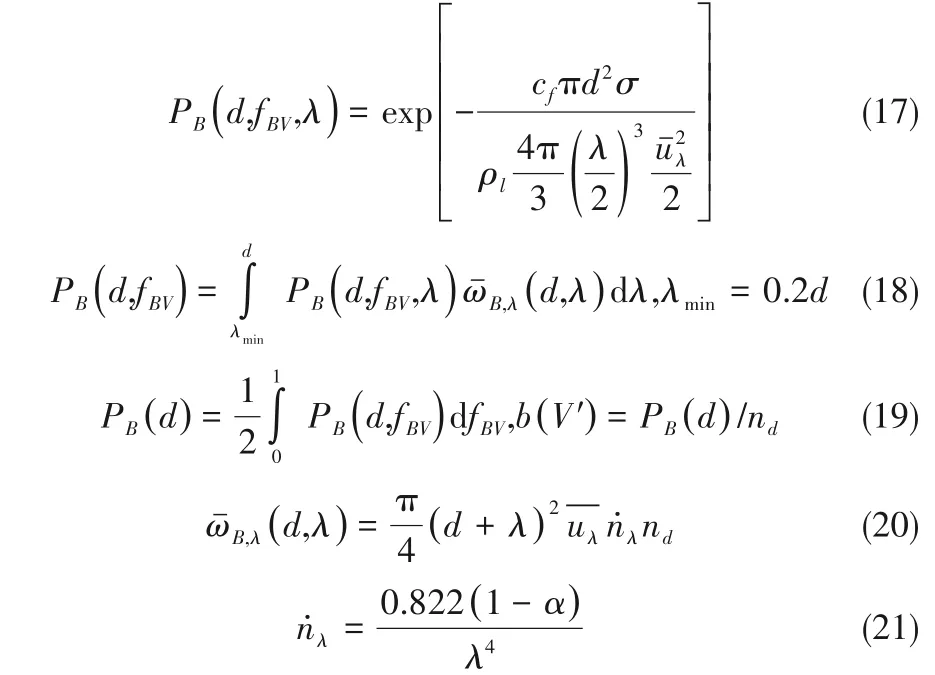
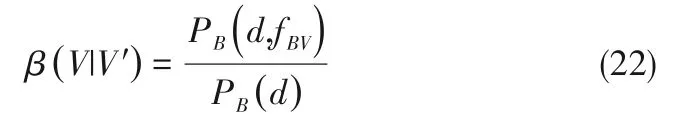
任意气泡V'破碎生成子气泡V的概率β(V|V')b(V'),即 破 碎 概 率PB(d,fBV)/nd的 最 终 形式为:
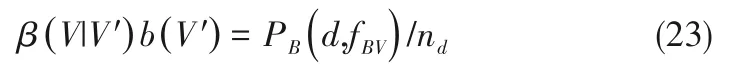
1.4.3 气泡合并模型 同样基于上述分析,本文采用Luo[12]的合并模型,该模型将气泡合并分为气泡与气泡碰撞、碰撞时两气泡的速度能否引起气泡合并两部分,将两气泡的合并概率分解为碰撞频率与合并效率之积:

2 数值方法
2.1 几何建模与网格划分
2.1.1 几何建模 基于张振铎[25]可视化研究的离心泵采用CFturbo10.3建立几何模型,主要参数如表1所示。并结合泵内流动特点,将计算流体域划分为如图1所示的四部分。
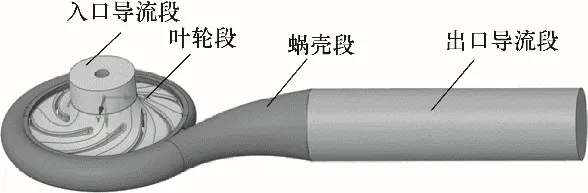
图1 离心泵流体域几何建模Fig.1 Geometric modeling of centrifugal pump fluid domain

表1 离心泵的主要设计参数Table 1 Parameters of centrifugal pump
2.1.2 网格划分 为保证仿真求解的稳定性与求解质量,本文针对上述四个流体域的不同几何特征采取相应的网格划分策略,应用Turbogrid对叶轮单流道划分结构化网格,并导入ICEM获得全流道结构化网格;应用ICEM对蜗壳段划分非结构化网格;应用ICEM对进出口延伸段划分结构化网格。为保证y+的值在壁面函数(与Realizablek-ε模型相匹配)适用的30~300内,对计算域的壁面网格设置膨胀层,并在计算中进行验证。此处网格划分使用的Turbogrid、ICEM与后续数值模拟所采用的Fluent均来自ANSYS 2020R2版本。
2.2 网格无关性验证
选取网格数以2倍率增长的四组网格对1500 r/min的单相流场进行求解,结果表明入口压力均大于40 kPa,满足忽略空化的假设,y+值在100以内,满足与Realizablek-ε模型相匹配的壁面函数的适用条件。该工况下实验获得的扬程值为4.36 m,仿真获得的扬程计算结果如图2所示,当网格数从0.68×106增加到1.25×106时,仿真与实验[30]的扬程偏差值从2.21%下降到2.18%,网格数进一步增加 到2.61×106、6.14×106时,偏差值基本都为2.18%。为保证计算精度且节约计算成本,本文采用网格数为2.61×106的划分方式。
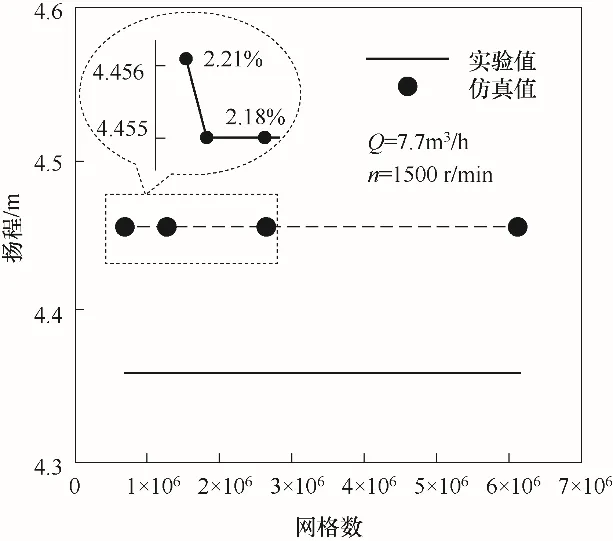
图2 1500 r/min工况网格无关性验证Fig.2 Mesh independence verification at 1500 r/min
2.3 TFM-PBM耦合数值模拟方案
根据前人[18,31-33]的可视化研究结果,离心泵内气泡尺寸在0.1~10 mm之间,将气泡尺寸离散如表2所示。并设计表3模拟方案,探究入口参数对泵内气泡尺寸的影响。模拟采用速度入口边界、压力出口边界,出口压力为标准大气压,监测的物理量为入口压力、出口流速。为提高计算的稳定性,仿真分为三步进行。首先,气液两相流采用非均质Euler-Euler模型,旋转流体域叶轮部分采用Frame Motion,对模型进行稳态数值计算;当计算残差小于10-4,且监测的物理量基本不变时,将叶轮部分的计算方法改为Mesh Motion,对模型进行瞬态数值计算,时间步长为0.00033(叶轮旋转3°);当监测物理量的波动稳定后,再加入PBM模型,对模型进行瞬态数值计算,当监测物理量的波动再次稳定后,数值计算完成。
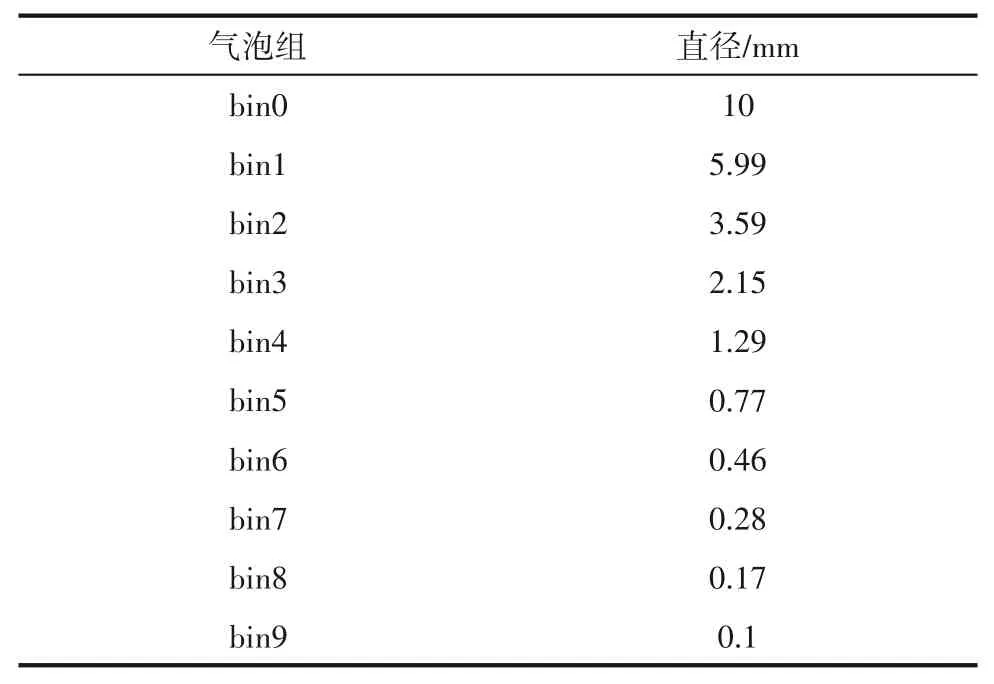
表2 PBM模型气泡尺寸离散Table 2 Discrete bubble sizes in PBM

表3 TFM-PBM数值模拟方案Table 3 TFM-PBM simulation scheme
3 计算结果与分析
3.1 TFM-PBM耦合数值模拟结果验证
图3为模型泵在转速为1500 r/min,入口体积气含率(IGVF)分别为0.32%、1.04%、2.21%、3.25%、4.86%时,TFM-PBM的数值解与文献[30]实验值的对比。
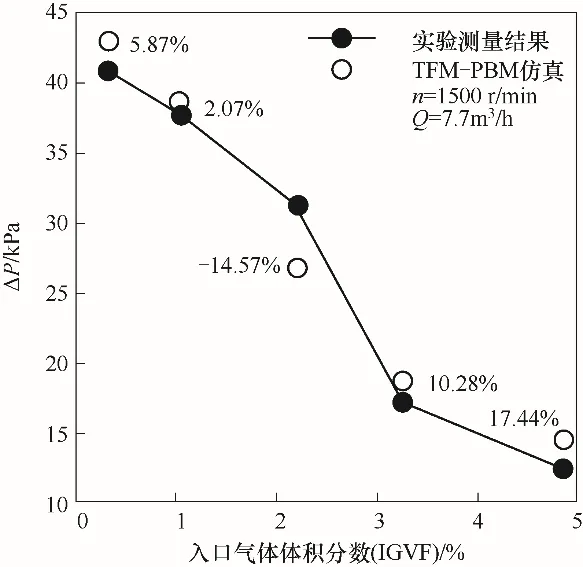
图3 扬程的TFM-PBM仿真结果与实验测量结果[30]对比Fig.3 Head comparison of TFM-PBM data and experimental values[30]
图3显示,当IGVF较小时,仿真相对误差较小;当IGVF超过2%时,相对误差逐渐增大。定义垂直于叶轮进口方向且位于叶轮出口截面50%高度处的叶轮截面为叶轮中心截面,进一步将叶轮中心截面的局部气含率分布与可视化结果[30]进行对比。结合式(6),由于气液密度不同,在叶轮旋转时,受叶轮旋转作用力fq,pump较大的液相更远离叶片压力侧,留下受fq,pump更小的气相,此时泵内气体聚集,引起流速下降,使得原本适用于高Reynolds数的湍流模型计算误差增大,但仍在误差允许范围内(±20%),CFD-PBM耦合模型对流场的压力变化计算有效,其用于修正两相界面面积的中间计算量(气泡尺寸分布)有效。
而截面上的相分布情况并非中心对称,其根本原因在于叶轮外部的蜗壳并非中心对称(图1)。实际上,图4中蜗壳出口位于右上方,越接近该处的液体更易因为叶轮旋转作用力fq,pump离开叶轮流道,进而引起该处气液相对流速增大,曳力增加,气相被拖曳变形更加明显。
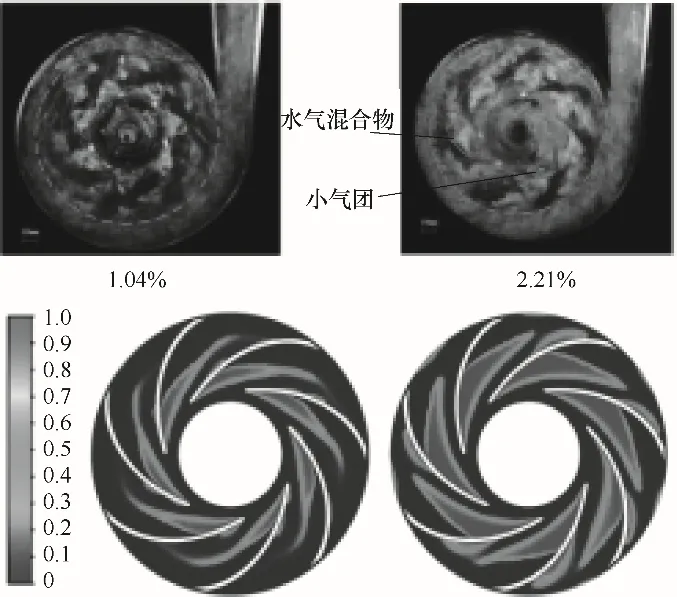
图4 相分布的TFM-PBM仿真结果与可视化结果[30]对比Fig.4 Phase distribution comparison of TFM-PBM data and visualization values[30]
3.2 IGVF对泵内气泡尺寸发展的影响
图5为模型泵在转速为1500 r/min、体积流量为7.7 m³/h(42%Qmax)、入口气泡尺寸为bin4(1.29 mm)的条 件下,IGVF分 别为0.32%、0.60%,1.04%、2.21%、3.25%、4.86%时,泵内沿程气泡尺寸随IGVF变化图。结果显示,在该条件下:
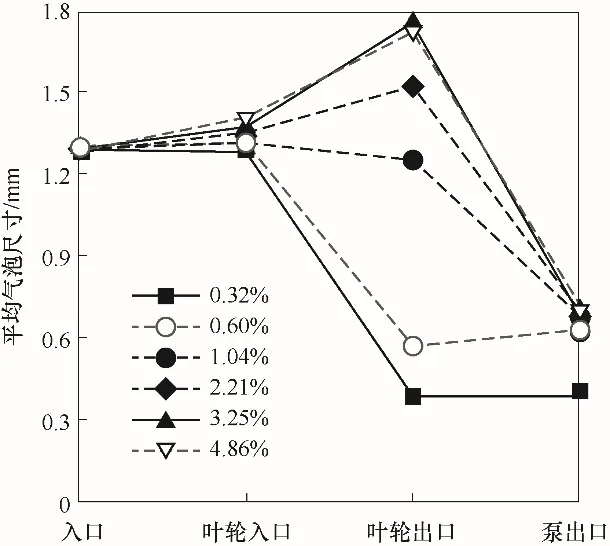
图5 泵内沿程气泡尺寸随IGVF变化(din=bin4)Fig.5 Average bubble size of each flow domain under different inlet gas volume fraction(din=bin4)
(1)当IGVF<1.04%时,气泡经叶轮尺寸减小,随着IGVF升高,气泡在叶轮内尺寸减小程度逐渐降低,叶轮出口气泡尺寸逐渐增大,但在蜗壳中尺寸又缓慢增大;
(2)当IGVF>1.04%时,随着IGVF升高,叶轮内气泡尺寸逐渐大于入口尺寸,并持续增长,但增长速度逐渐变缓。此时蜗壳内气泡尺寸始终呈下降趋势,下降速度逐渐加快;
(3)泵出口平均气泡尺寸随IGVF的增大而增大,但总体上均小于入口。
在1800 r/min时有相似的变化规律,下面通过分析IGVF对气泡在叶轮、蜗壳内尺寸变化的影响机理,揭示IGVF对出口气泡尺寸的影响规律。
3.2.1 IGVF对叶轮内气泡尺寸发展的影响机理 气泡破碎由湍流涡的碰撞引起,Luo等[12-13]的模型假设尺寸为λ到λ+dλ的湍流涡的能量E(λ)服从指数分布,且当碰撞时的E(λ)满足一定条件时气泡才会破碎,因此碰撞的频率与碰撞时的E(λ)共同决定气泡破碎频率。尺寸为d到d+dd的气泡与尺寸为λ到λ+dλ的湍流涡的碰撞频率ωˉB,λ(d,λ)由式(20)计算;碰撞后能发生fBV破碎(即破碎后一个子气泡的体积与原体积的比值为fBV)的破碎效率PB(d,fBV,λ)由式(17)计算。将碰撞频率与破碎效率相乘,获得尺寸为d到d+dd的气泡与尺寸为λ到λ+dλ湍流涡碰撞并发生fBV破碎的有效破碎频率ω(B):
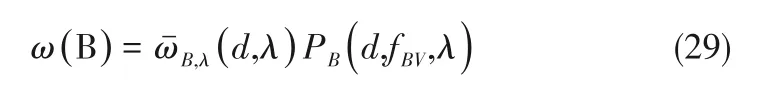
同理,气泡合并由气泡之间的碰撞引起,当碰撞时两气泡的速度满足一定条件时,气泡才会合并。尺寸为di、dj的两组气泡的碰撞频率由式(25)计算,碰撞后能发生合并的效率Pc(di,dj)由式(28)计算。将碰撞频率与合并效率相乘,获得尺寸为di、dj的两组气泡能发生碰撞合并的有效合并频率ω(C):
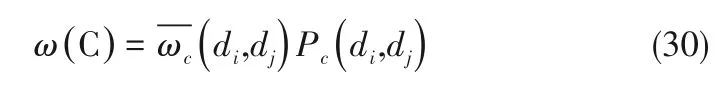
由于ω(B)、ω(C)均含有数密度,而数密度nd与气泡尺寸d、气相体积流量Qg相关,气相体积流量Qg又是总体积流量Q与体积气含率(α)的函数,为更直观反映体积气含率(α)、气泡尺寸(d)对ω(B)、ω(C)的影响,利用气相质量守恒方程将数密度nd表示为α与d的关系式,对单位体积有:
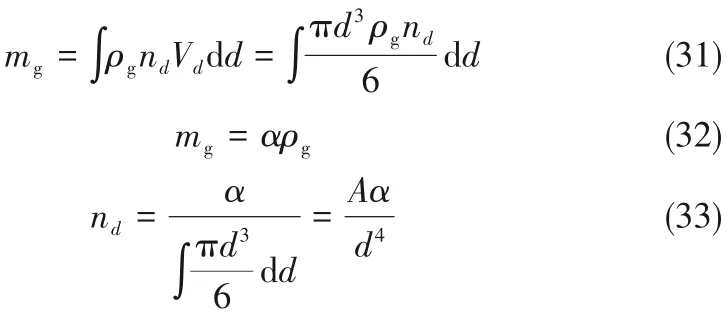
式中,Vd为直径为d的气泡的体积,m3;A为一个常数;nd为尺寸为d到d+dd的气泡的数密度,即单位体积内相应尺寸气泡的个数,1/m³。将式(17)、式(20)、式(33)代入式(29),并将λ用d的倍数表示,化简中常数项用系数X′、X′′表示,有:
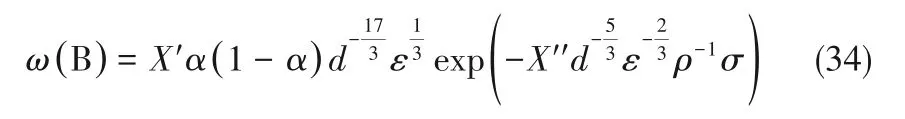
同理,将式(25)、式(28)、式(33)代入式(30),并将di与dj均表示为d的倍数,化简时常数项用系数Y′、Y′′表示,有:
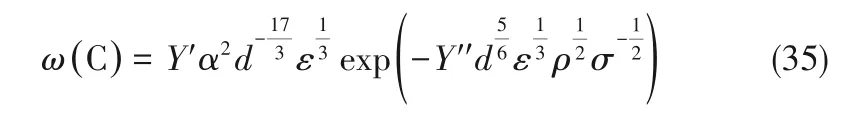
仅考虑体积气含率α对ω(B)、ω(C)的影响,将式(34)、式(35)中的其余无关量简化为X、Y:
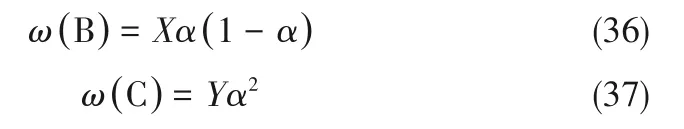
图6为ω(B)、ω(C)随体积气含率α的变化,如忽略其他因素对气泡破碎合并的影响,可近似有X=Y。首先用图6解释图5中随IGVF升高,叶轮出口气泡尺寸由先小于入口气泡尺寸逐渐增大至大于入口气泡尺寸。IGVF改变,会引起叶轮流道的体积气含率发生改变,考虑图4中叶轮内气体聚集,提取出各IGVF对应的叶轮中心截面的平均体积气含率,并其将对应的ω(B)、ω(C)标注到图6曲线上。发现当IGVF较低时,聚集量较小,ω(B)大于ω(C),此时气泡趋于破碎,随着IGVF增大,总体破碎趋势减缓,气泡尺寸变大。当IGVF较高时,叶轮内局部气含率骤增,ω(C)>ω(B),且ω(C)加速增长,ω(B)加速减小,此时气泡趋于合并,合并的强度逐渐增强,此时叶轮出口气泡逐渐增大。因此,随IGVF增大,叶轮内的气泡呈现出图5所示的变化趋势。
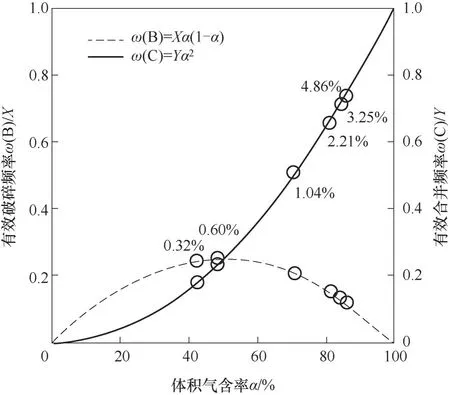
图6 有效破碎频率ω(B)、有效合并频率ω(C)随体积气含率(α)的变化Fig.6 Effective break-up frequencyω(B)and effective coalescence frequencyω(C)under different gas volume fractionα
3.2.2 IGVF对蜗壳内气泡尺寸发展的影响机理 同理,提取各IGVF对应的蜗壳中心截面平均气含率,发现其值与IGVF基本一致,对应图6中0<α<5%的部分,此时仍是破碎主导,气泡尺寸逐渐减小。但在图5中,当IGVF<1.04%时,蜗壳中气泡尺寸反而增大,这表明仅考虑气含率的图6在判断此时蜗壳中的气泡破碎合并存在缺陷。回到原始的式(34)、式(35),影响ω(B)、ω(C)大小的因素还有气泡尺寸d、湍流耗散率ε、液相密度ρ、表面张力σ,其中气泡尺寸d、湍流耗散率ε是随流动过程变化的,如图5中的气泡尺寸,此时简化为X、Y会对ω(B)、ω(C)二者进行比较时产生影响。根据Luo等[13]的研究有X'=Y'=0.923,将X、Y中的共有部分记作Z,。
由图5可知,随IGVF增大,叶轮出口气泡尺寸逐渐增大,则相应的蜗壳入口气泡尺寸逐渐增大,提取蜗壳内的湍流耗散率如表4所示,可以发现此时蜗壳内的湍流耗散率也随IGVF的增大而增大。结合式(34)、式(35)可知,随着气泡尺寸d、湍流耗散率ε的增大,ω(B)增大、ω(C)减小,导致图6中ω(B)、ω(C)曲线的交点右移,如图7所示。

表4 蜗壳内湍流耗散率随IGVF变化Table 4 Turbulent dissipation rate of impeller and volute under different inlet gas volume fraction
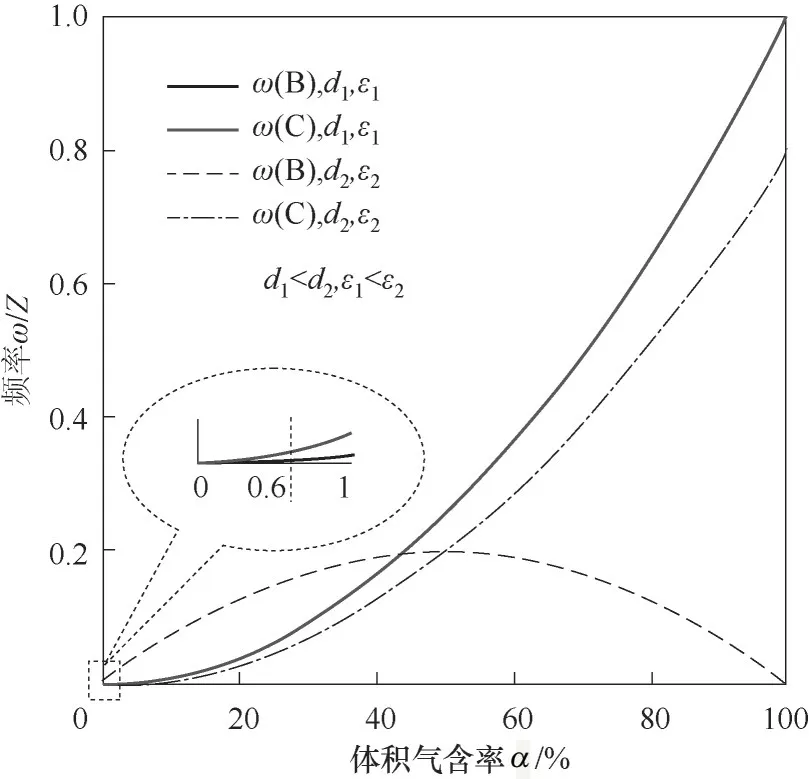
图7 有效破碎频率ω(B)、有效合并频率ω(C)随体积气含率(α)的变化Fig.7 Effective break-up frequencyω(B)and effective coalescence frequencyω(C)under different gas volume fractionα
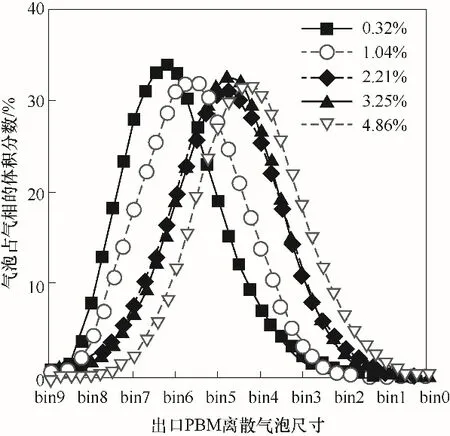
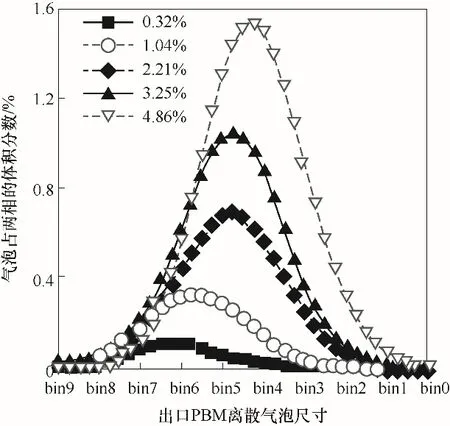
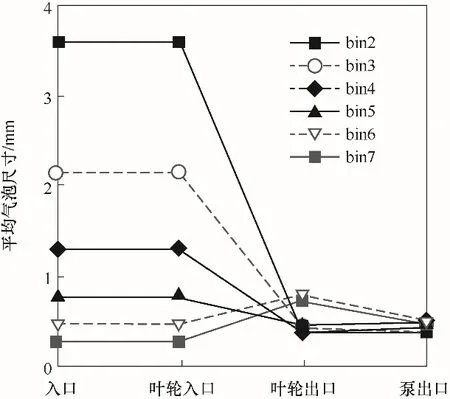
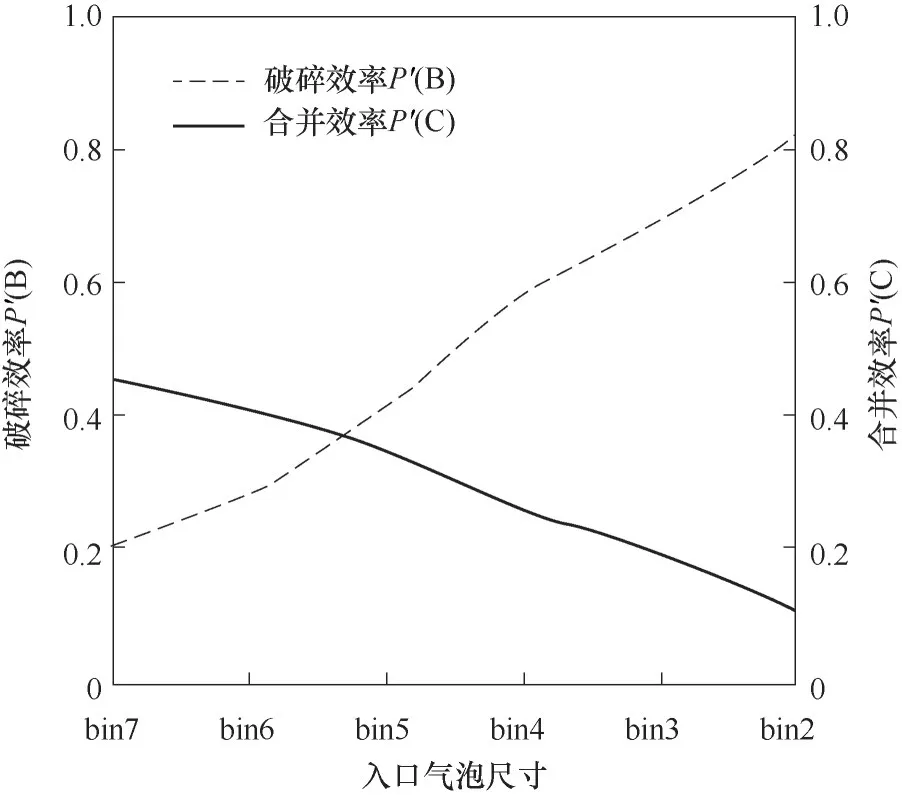
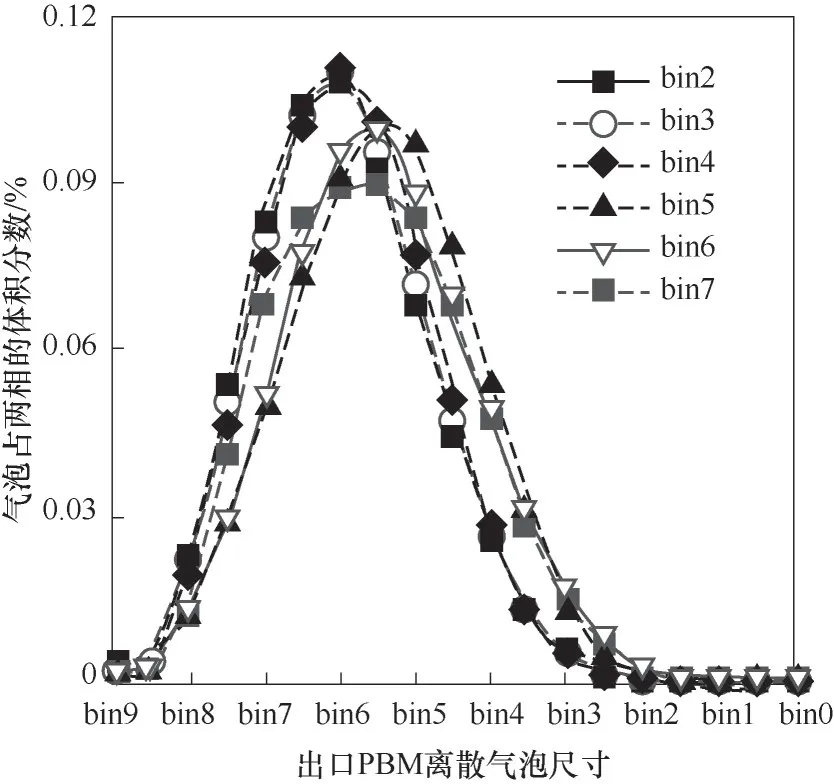
因此在IGVF较小的情况下,ω(C)会在更小的气含率时超过ω(B),从而出现图5中蜗壳内气泡尺寸在IGVF<1.04%时反而增大的现象。另一方面,在1.04% 3.2.3 IGVF对泵出口气泡尺寸分布的影响规律实际应用更关心泵出口气泡尺寸分布,图8为泵出口气泡数密度分布随IGVF变化,此时随IGVF升高,出口小气泡数目逐渐减少,大气泡数目逐渐增多。 图8 泵出口气泡数密度分布随IGVF变化(din=bin4)Fig.8 Bubble number density distribution at outlet of pump under different IGVF(din=bin4) 实际应用除了考虑小气泡的数密度nd,还会考虑小气泡的总体积。图9为泵出口各尺寸气泡占气相的体积分数ndVd/Qg随IGVF变化,反映了不同IGVF时各尺寸气泡占气相体积分数的变化。图10为泵出口各尺寸气泡占两相的体积分数ndVd/(Qg+Ql)随IGVF变化,反映了不同IGVF时各尺寸气泡占两相总体积分数的变化,在总体积流量一定时,它就是各尺寸气泡总体积的变化。由于出口的体积气含率与IGVF基本相同,这两个体积分数的计算方式如下: 图9 泵出口气泡尺寸分布随IGVF变化(占气相,din=bin4)Fig.9 Bubble size distribution at outlet of pump under different inlet gas volume fraction(by air,din=bin4) 图10 泵出口气泡尺寸分布随IGVF变化(占两相,din=bin4)Fig.10 Bubble size distribution at outlet of pump under different inlet gas volume fraction(by two-phase,din=bin4) 由图8、图9可知,此时随IGVF升高,出口气泡尺寸分布明显右移,大气泡个数增多,气泡尺寸逐渐增大,这与上述机理分析的结果一致。另一方面,式(38)表明尺寸为d的气泡占气相的体积分数与d正相关。因此虽然图9显示小尺寸的气泡数密度nd较大,但图9中体积分数最大的是中等尺寸气泡。如以出口尺寸小于bin6(0.46 mm)的气泡总体积量最大为筛选目标,即小于该尺寸的气泡占两相体积分数之和最大,图10显示IGVF=3.25%时达到最优。 为进一步探究入口气泡尺寸对出口气泡尺寸、气泡数密度的影响,本文求解了在1500 r/min、7.7 m³/h(42%Qmax)条件下,IGVF分别为0.32%、3.25%、4.86%时,入口气泡尺寸分别为bin2(3.59 mm)、bin3(2.15 mm)、bin4(1.29 mm)、bin5(0.77 mm)、bin6(0.46 mm)、bin7(0.28 mm)时的泵内气泡尺寸分布。图11为IGVF=0.32%时泵内沿程气泡尺寸随入口气泡尺寸变化,结果显示,在该条件下: 图11 泵内沿程气泡尺寸随入口气泡尺寸变化(IGVF=0.32%)Fig.11 Average bubble size of each flow domain under different inlet bubble size(IGVF=0.32%) (1)当入口气泡尺寸较小时,气泡经叶轮尺寸变大; (2)入口气泡尺寸较大时,气泡经叶轮尺寸减小,且入口气泡尺寸越大,尺寸减小的幅度越大; (3)总体上出口平均气泡尺寸基本不变。 下面通过分析入口气泡尺寸对气泡在叶轮、蜗壳内尺寸变化的影响机理,揭示其对出口气泡尺寸的影响规律。 3.3.1 入口气泡尺寸对气泡尺寸发展的影响机理结合式(34)、式(35)可知,在转速、入口气含率不变时,入口气泡尺寸变化对ω(B)、ω(C)会产生影响,且均包含两个影响因子,其中第一个影响因子均为d-17/3,而另一个影响因子为包含d的幂函数形式。 第一个影响因子实际为碰撞频率,由式(33)可知,其他条件不变时,气泡数密度正比于d-4,而湍流涡尺寸λ可表示为d的倍数,代入式(20)有ωˉB,λ(d,λ)与d-17/3正相关,即ω(B)的第一个影响因子。同理有与d-17/3正相关,即ω(C)的第一个影响因子。这一影响因子表明在气含率一定时,入口气泡尺寸变化对气泡与湍流涡的碰撞频率、气泡与气泡的碰撞频率影响一致。因此气泡的破碎合并主要由第二个影响因子决定。 同第一个影响因子的分析,第二个影响因子实际为碰撞后破碎、合并的效率,分别记作P′(B)、P'(C)。气泡在bin7(0.28 mm)到bin2(3.59 mm)尺寸范围内,如图12所示,随着气泡尺寸d的增加,破碎效 率增 大,而 合 并 效 率减小。 图12 叶轮内破碎效率P′(B)、合并效率P′(C)随入口气泡尺寸的变化(IGVF=0.32%)Fig.12 Break-up efficiency P′(B)and coalescence efficiency P′(C)in impeller under different inlet bubble size(IGVF=0.32%) 在IGVF=0.32%条件下,叶轮流场内无明显气体聚集。结合图12可知,当气泡尺寸较小时(d 3.3.2 入口气泡尺寸对泵出口气泡尺寸分布的影响规律 图13为IGVF为0.32%时出口气泡尺寸分布随入口气泡尺寸变化,图中显示随入口气泡尺寸增大,出口气泡尺寸分布先右移后左移,出口尺寸先增大后减小,但总体尺寸相差很小,与上述影响机理分析的结果一致。如以出口尺寸小于bin6(0.46 mm)的气泡占两相体积分数为优化目标,入口气泡尺寸为bin2(3.59 mm)时达到最优。 图13 泵出口气泡尺寸分布随入口气泡尺寸变化(占两相,IGVF=0.32%)Fig.13 Bubble size distribution at outlet of pump under different inlet bubble size(by two-phase,IGVF=0.32%) 图14为IGVF为3.25%时出口气泡尺寸分布随入口气泡尺寸变化,图中显示随入口气泡尺寸增大,出口气泡尺寸分布基本不变,在IGVF为4.86%时有相同结果。结合入口气含率对泵内气泡尺寸变化的机理分析,可以发现此时叶轮内气体大量聚集,入口气泡尺寸对出口气泡尺寸的影响基本无法体现,此时出口气泡分布主要由IGVF决定。 图14 泵出口气泡尺寸分布随入口气泡尺寸变化(占两相,IGVF=3.25%)Fig.14 Bubble size distribution at outlet of pump under different inlet bubble size(by two-phase,IGVF=3.25%) 本文为探究离心泵内微气泡的发生特性,将含气泡的泵内两相流动拆解为气液两相流、旋转流场、气泡破碎合并三个部分,并建立TFM-PBM耦合模型求解泵内流场参数,获得气泡尺寸分布。在此基础上,依据Luo等的模型,分别模拟模型泵在不同IGVF、不同入口气泡尺寸下的内部流动,通过逐层分析气含率、气泡尺寸对气泡在叶轮、蜗壳内尺寸变化的影响机理,揭示其对出口气泡尺寸的影响规律。具体结论如下。 (1)不同IGVF时,扬程与叶轮内平均气泡尺寸的数值结果与实验数据较吻合,TFM-PBM耦合模型对离心泵内气泡尺寸计算具有较好的适用性。 (2)IGVF升高引起叶轮内气体聚集是影响气泡发展的主要因素。在IGVF较低时,泵内基本无气体聚集,随IGVF升高,叶轮内引起破碎的碰撞频率高于引起合并的碰撞频率,气泡趋于破碎,叶轮出口气泡尺寸小于泵入口,此时蜗壳内气泡尺寸对气泡破碎合并的影响开始显现,气泡又趋于合并。当气含率较高时,泵内气体聚集引起局部气含率升高,随IGVF升高,聚集加剧,叶轮内引起破碎的碰撞频率低于引起合并的碰撞频率,气泡趋于合并,叶轮出口气泡尺寸大于泵入口,而在蜗壳内气含率恢复正常,气泡又趋于破碎。 (3)入口气泡尺寸对出口气泡尺寸的影响对IGVF较为敏感。当IGVF较低时,受入口气泡尺寸与气含率共同影响,随入口气泡尺寸增大,出口气泡尺寸先增大后减小;而当IGVF较高时,泵内气体开始聚集,气含率的影响占主导地位,入口气泡尺寸对出口气泡尺寸影响不明显。 (4)对本文研究的模型泵而言,以出口尺寸小于bin6(0.46 mm)的气泡占两相体积分数为优化目标,在转速为1500 r/min条件下,IGVF=3.25%达到最优,并且基本与入口气泡尺寸无关。 (5)在入口条件一致时,叶型改变也会影响叶轮内的局部气含率与湍流耗散率,因此可以考虑修改叶型实现改变气泡尺寸的目的。 符号说明 cf——气泡表面积增加系数,cf=fBV2/3+(1-fBV)2/3-1 di,dj——分别为体积为Vi、Vj的气泡的直径,m fBV——气泡破碎体积分数,即破碎后一个子气泡的体积V与原体积V'之比,fBV=V/V' k——湍流动能,m2/s2 n——离心泵的转速,r/min nd,ndi,ndj——分别为直径为d、di、dj的气泡的数密度,即单位体积内相应气泡的个数,1/m³ ——尺寸为λ的湍流涡的数密度,1/m³ Qmax——转速不变时的最大体积流量,m3/h tdrainage——直径为di、dj的两气泡碰撞后,接触面的厚度下降为临界厚度所需的时间,s ,——分别为直径为di、dj的 气 泡 的 平均湍动速度,m/s ——直径为di、dj的气泡间的平均相对湍动速度,m/s ——尺寸为λ的湍流涡的平均湍动速度,m/s Weij——直径为di、dj的两气泡碰撞时的Weber数,即惯性力与表面张力之比 xij——直径为di、dj的两气泡的直径之比,xij=di/dj y+——第一层网格质心到壁面的无量纲距离 αin——入口气体体积分数 β——经验参数,文中为2.047 ε——湍流耗散率,m2/s3 λ——湍流涡的尺度,m ξ——湍流涡尺寸与气泡直径之比,ξ=λ/d σ——表面张力,文中空气-水体系的表面张力为0.07 N/m τcontact——直径为di、dj的两气泡碰撞后的接触时间,s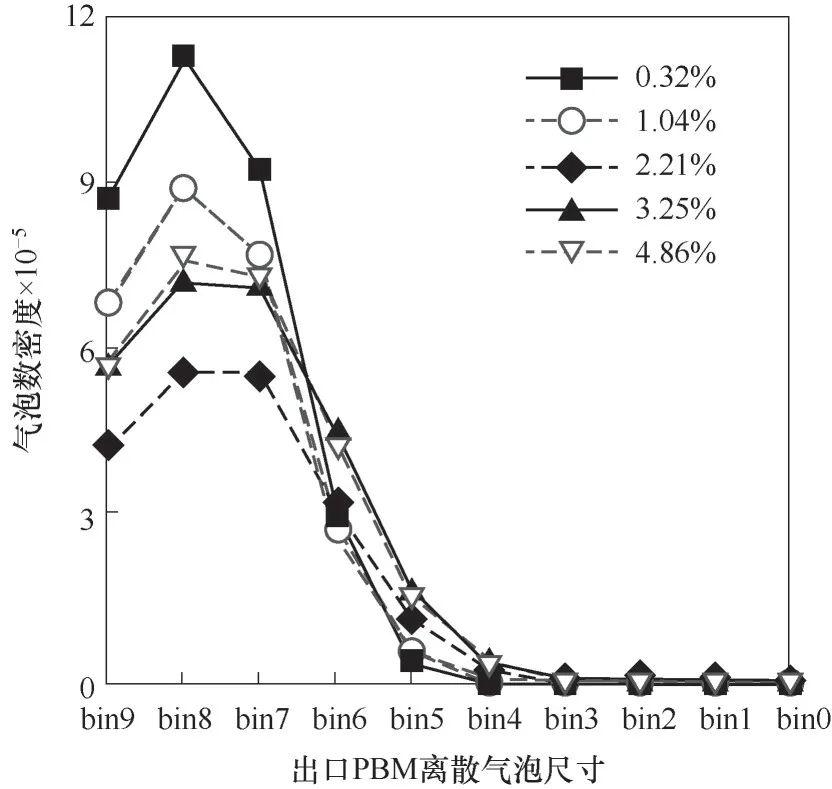

3.3 入口气泡尺寸对泵内气泡尺寸发展的影响

4 结 论
