城市轨道交通多交路共线运营客流分配方法

许得杰，巩亮，朱宁，王雪鑫

(1.兰州交通大学，交通运输学院，兰州730070；2.天津大学，管理与经济学部，天津300072；3.中铁第一勘察设计院集团有限公司，西安710064)

0 引言

随着我国城市轨道交通网络化运营的不断深入，多交路共线运营和互联互通的跨线运营需求日益增强。研究多交路共线客流分配问题对城市轨道交通复杂交路设计、列车开行方案的编制和优化调整等具有重要意义。

目前，针对城市轨道交通客流分配问题已有深入研究。在网络客流分配方面，文献[1]构建了无缝换乘条件下的轨道交通网络客流分配模型；文献[2]提出了考虑乘客多路径出行选择的客流概率分布模型和基于深度优先的路径搜索算法；文献[3]考虑影响乘客路径选择的主要因素，提出了基于改进Logit模型的网络客流分配方法。在共线运营客流分配方面，早期研究主要针对常规公交共线运营的客流分配问题。该问题最早由Chriqui等[4]提出，并将其称为共线问题。随后Nguyen 等[5]提出了基于超图理论的共线问题优化模型；Spiess 等[6]假定乘客选择乘坐第一趟到站公交，提出了共线问题及其均衡配流问题的线性规划模型；Correa 等[7]提出了拥挤条件下的共线问题和客流分配方法；Cominetti等[8]提出了能力约束下的共线网络均衡分配模型。在轨道交通方面，共线运营客流分配方法主要应用在开行方案[9-10]的优化研究中，乘客在不同交路列车间的换乘在多交路共线运营中普遍存在，因此客流分配要能够刻画乘客换乘行为，而既有客流分配方法对乘客的换乘行为考虑不足，且提出的方法仅适用于某种特定的交路形式，当同类型交路的形式发生变化时，既有方法将不再适用，故其可拓展性和适用性存在一定的局限性。

综上，本文分析城市轨道交通典型的多交路运营形式，充分考虑交路形式变化以及乘客在不同交路列车间的换乘行为，提出两种多交路共线运营客流分配方法。一是基于发车频率和乘客出行区段划分的客流分配方法，该方法可以适用大小交路、衔接交路，以及这两种交路组合而成的典型混合交路形式；二是基于超路径的客流增量分配方法，该方法可以适应多交路与快慢车、多交路与多编组等组合运营模式的客流分配。多交路客流分配可得到不同交路列车在不同区段承担的客流量，该客流量用于计算交路计划中不同区段的列车发车频率，可以为长大线路和复杂线型的多交路设计，以及跨线运营、快慢车、市域铁路(城际铁路)与地铁贯通运营等共线运营模式的开行方案和交路优化奠定基础。

1 共线运营及其多交路形式

多交路运营指针对较长线路上客流分布的空间差异性，某一运营商在同一线路上开行2种及以上交路形式列车的运输组织方法。多交路运营会产生不同交路列车占用相同区段运行的情况，即共线运营。多交路共线运营交路可分为两类：一是为解决客流空间分布的差异性，在直线型线路上采用的多层交路的嵌套和叠加，包括典型的大小交路(嵌套交路)和衔接交路，以及由这两种交路组合而成的混合交路等形式；二是为连接不同方向上的客流集散点，在规划设计阶段形成的含支线路上采用干线和支线共线运营的模式，即Y型交路。典型共线运营多交路如图1所示，其中，s0、s1为小交路折返站，si为中间站，sE、sF和sN为终点站。

图1 典型共线运营多交路Fig.1 Typical multiple routings for common-line operation

以图1(a)为例，该交路的4种变化形式(不含单一交路)如图2所示。其中图2(a)～(c)中小交路折返站位置s0≤s1，图2(d)中小交路折返站s0>s1。为方便表述，本文将图1中的共线交路形式称为典型形式，将图2 中的共线交路形式称为一般形式，并以图1(a)混合交路为例构建客流分配模型，Y 型交路可采用相同思路。

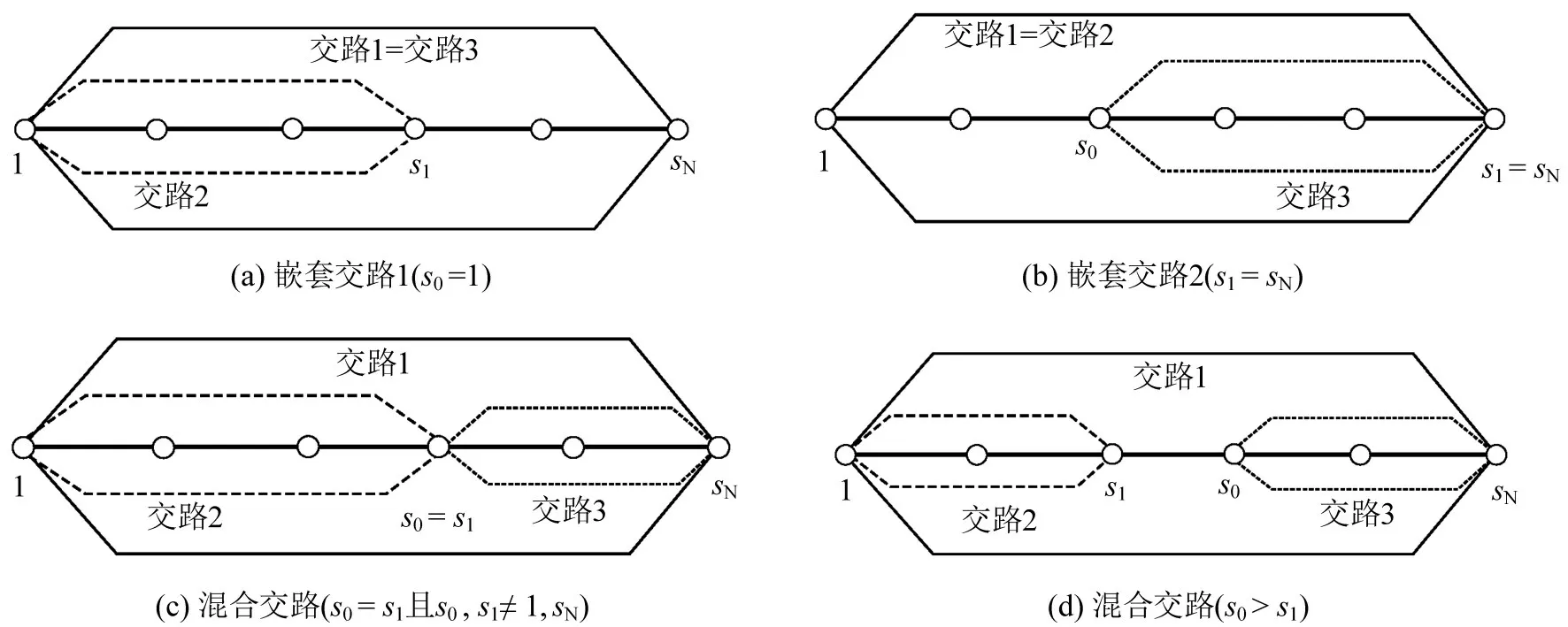
图2 共线运营多交路一般形式Fig.2 General types of multiple routings for common-line operation

2 基于发车频率和乘客出行区段划分的客流分配方法

基于发车频率和乘客出行区段划分的客流分配方法主要包含两个关键问题：一是根据多交路共线运营的形式，按乘客出行区段，将OD 客流进行分类；二是根据乘客出行区段，按照发车频率确定分类客流在不同交路列车上的客流分担比例。

2.1 假设条件

根据多交路共线运营特征，模型基本假设如下：

(1)轨道交通列车交路形式和开行方案已知，发车频率满足高发车频率要求，即发车间隔小于12 min。

(2)乘客到达服从均匀分布。

(3)对于共线运营区段的跨交路出行乘客，假定该部分乘客具有选择直达列车的选择偏好，即如果第一趟到站列车为非直达列车，乘客会因为避免换乘而继续等待下一趟直达列车。

(4)若乘客选择乘坐跨交路列车出行，即需要在不同交路间换车，则乘客选择在小交路终点站下车，不会提前下车。

(5)乘客的路径选择策略相同，因此乘客是否滞留站台不影响客流分配结果。

(6) 列车运行图的发车频率满足发车比例约束，且发车间隔均匀。

2.2 乘客出行区段划分及客流分配模型构建

以图1(a)所示混合交路为例，以小交路折返站为界，将客流按照出行区段划分为6 类，如图3 所示。其中，第I类、II类和III类客流O点均位于车站区间[1,s0)，第IV 和第V 类客流O 点位于[s0,s1)，第VI类客流OD均位于[s1,sN]。

图3 客流出行区段划分Fig.3 Trip section divisions of passenger flows

根据图1(a)中共线区段中的运营交路情况，可将全线断面k ∈[1,sN) 分为3 部分：1 ≤k ≤s0-1、s0≤k ≤s1-1 和s1≤k ≤sN-1。其中第1和第3部分区段分别由交路1和2、交路1和3共线运营，第2部分区段由交路1、2 和3 共线运营。令Qrk,h表示交路h 的列车在第k 个断面rk上分担的客流量，dij为车站i 到j 的客流需求。根据断面位置k 与折返站s0和s1的关系，以上行方向为例，Qrk,h的计算方法如下。

式中：第1～3项分别表示第I类、第II类和第III类客流；β1～β9为各交路列车在不同区段的客流分担率，反映乘客对路径的选择行为。本文采用基于发车频率的路径选择行为，路径选择基于优化策略(Optimal Strategy)[6]，即乘客在出行前不会选择某条具体的路径，而是在出行过程中从优化策略中选取其中一条路径，优化策略中各条路径的客流分担率是基于发车频率计算的。因此，优化策略可以理解为在某种特定的路径选择策略下得到的备选路径集合。

以图3 中第1 部分区段的客流(第I、II 和III 类客流)为例，说明乘客路径选择策略及β1和β2的取值。对于第I 和第II 类客流，均可以乘坐交路1 和交路2的列车(备选路径集合为交路1和交路2)，故这两类客流由交路1 和交路2 列车分担；对于第III类客流，根据假设条件(3)，乘客可以优先选择乘坐交路1的直达列车，或者先乘坐交路2的列车，至交路2 的折返站s1车站下车后，再乘坐交路1 的列车至目的地。根据假设条件(4)，乘坐非直达列车的乘客在小交路终点站下车，不会提前下车，故第III类客流在区段1～ s0上，分别由交路1 和交路2 分担，但需要考虑乘客对直达列车的选择偏好。令f1、f2和f3分别表示交路1、交路2和交路3的发车频率，p 表示乘客选择偏好，则β1和β2为

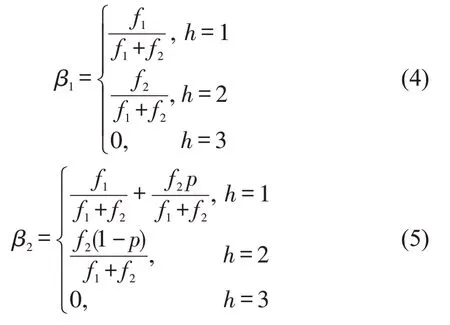
参数β3～β9表示为

式中：p ∈[0,1]，当p=0 时，表示第III 类客流不具有直达列车选择偏好，候车乘客来车即上；当p=1时，所有乘客均选择乘坐直达列车。式(2)中第4项表示第V类客流的分配方法，第V类客流的路径选择策略有3种：乘坐交路1或交路3的直达列车；或者先乘坐交路2的列车，到达折返站s1后再换乘交路1或交路2的列车至目的地。 β∙6中参数p′∈[0,1]表示第V类客流选择乘坐交路1和交路3的直达列车偏好概率，p′=0 表示来车即上，p′=1 表示只乘坐直达列车。因此，交路1 和交路3 的列车分担的客流包括两类：一是到站第一趟列车为交路1和交路3 的直达列车所分担的客流，分担比例分别为；二是到站列车为交路2的非直达列车，此时部分乘客选择继续等候下一趟直达列车，该部分乘客比例为由交路1 和交路3 列车分担，分担比例分别为和，由交路2的列车分担客流的比例为。

从式(4)～式(12)可以看出，对于∀βi,i=1,…,9，，其中，βi,h为交路h 的分担率，该等式表明：对任意断面而言，断面客流由覆盖该断面的所有交路分担，即满足流量守恒约束。若该等式不成立，则不满足流量守恒约束。共线运营多交路一般形式是典型共线交路的特殊形式，其客流分配方法与典型共线运营交路形式下的方法类似，因此不再赘述。

上述基于乘客出行区段划分的方法中，客流分担率仅与各交路的发车频率和乘客对直达列车的选择偏好有关，未能反映分担率与列车容量之间的关系。且该方法中乘客路径选择策略相同，即同一OD 的客流均选择相同的出行路径，未考虑路径的阻抗变化对乘客出行路径选择的影响，也未考虑各交路列车的载客能力约束，且针对更为复杂的三层及以上交路叠加形式，客流分担率的确定将变得非常困难，对快慢车、多编组开行方案下的客流分配也不再适用。因此，本文提出基于超路径的客流增量分配方法。

3 基于超路径的客流增量分配方法

基于超路径的客流增量分配方法主要涉及多交路共线运营服务网络、有效路径的选择和基于Logit模型的乘客路径选择模型3个关键问题。

3.1 多交路共线运营服务网络

假定多交路共线服务网络为G=(N,E)，N 和E 分别为节点集合和弧段集合，N 包括车站节点集合Ns和交路节点集合Nr，即N=Ns⋃Nr；E 包括候车弧、下车弧和乘车弧，这3 类弧中的车是指交路上的列车；弧的权重为阻抗，候车弧阻抗为候车时间；乘车弧阻抗为考虑乘客拥挤感知的乘车时间；下车弧为乘客下车后的出站时间或下车后到换乘站台的走行时间，由于共线运营中一般为同站台换乘，故走行时间为0。以图1(a)的中间站si为例，对于交路1和交路2的共线区段(仅上行方向)，车站节点si对应的交路节点有和，如图4 所示，si至和的有向弧为候车弧(因候车弧可以替代上车弧，故省去上车弧)。相反地，和至si的弧为下车弧，相邻2 个交路节点间的弧为乘车弧。据此，将多交路运营线路的所有车站转化为服务网络节点表示方法，即可将多交路共线运营的物理网络转化为服务网络。由图1(a)多交路转化的共线运营服务网络如图5 所示，图中，e1～e33为服务网络弧段标号。为方便后续算法中的递归调用，节点标号采用头节点小于尾节点的方式。

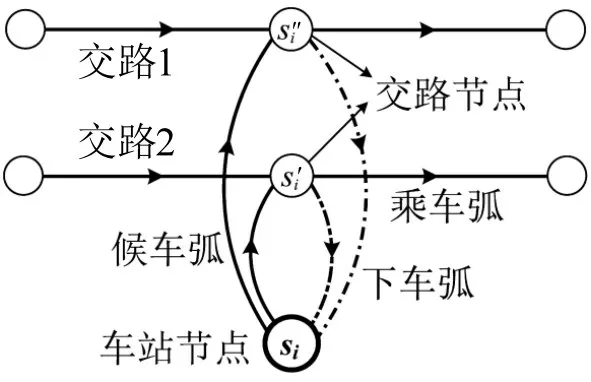
图4 服务网络的车站表示方法Fig.4 Stop representation of service network

图5 多交路共线运营服务网络Fig.5 Service network of multiple routings for common-line operation

3.2 有效路径的选择

(1)超路径的概念

②节点o 无前驱节点，d 无后继节点；

③对于任意节点i ∈Np-{o,d}，如果该节点不为车站节点，则最多有一个后继节点；

④ ηp满 足∀eij∈Ep，ηij,p表示从节点i出发的乘客选择弧段eij的概率。

图6为连接(o,d)的一条超路径，共包含3条基本路径，路径1：o →i1→i4→i7→d ；路径2：o →i2→i3→i5→i8→d ；路径3：i3→i6→i9→d 。可以看出，超路径是一个路径树，包含至少一条连接o和d 的基本路径，这与一般路径有所区别。超路径的意义在于，对于共线运营服务网络，乘客出行策略假设为：乘客出行时会选择可达路径中期望出行时间最短的路径。期望出行时间最短的路径集合即最短超路径，故乘客路径选择问题可转化为基于服务网络的最短超路径问题，求解最短超路径问题即可得到流量加载的有效路径。

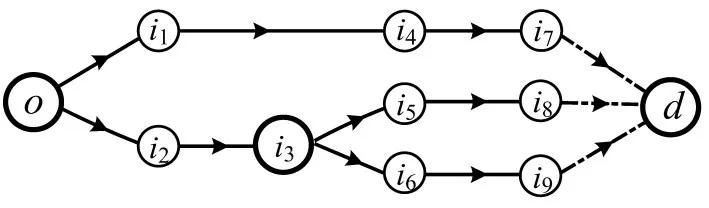
图6 超路径示例Fig.6 An example of hyperpath

(2)有效路径的选择方法

对轨道交通服务网络而言，乘客出行的有效路径是流量加载的基础。与基于乘客出行区段划分的客流分配方法的优化策略含义相同，有效路径也是一个备选路径集合，该有效路径为最短超路径中包含的基本路径。对多OD 对有向服务网络G=(N,E)，任意交路乘车弧e ∈E 的服务频率为fe，区间出行费用te(ve)是乘车弧e 上的与流量相关的旅行时间。由于轨道交通服务频率一般不受客流变化影响，故服务频率为定值。列车内的拥挤程度是影响乘客路径选择行为的关键因素，故区间出行费用需要考虑乘客的在车拥挤感知费用。考虑服务网络G 中任意OD 对(i,d)，假定存在从i 至d 的有向超路径(i ≠d)。从i 至d 的期望总出行时间τid可以表示为广义贝尔曼方程(Generalized Bellman Equations)[5,7]，即

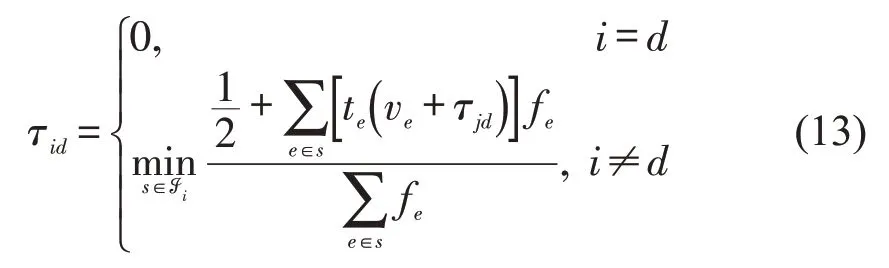
式中：ℐi为策略S ⊆的集合；={e ∈E:∙i(e)=i}为节点i 的向前星(出射弧)，其中i(e)为弧段e 的尾节点；τjd为节点j 至d 的旅行时间；te(ve)为与流量ve相关的拥挤感知时间，拥挤会导致乘客感知时间差异，从而影响乘客路径选择行为[1]。求解从i至d 的有效路径(最短超路径)等价于求解贝尔曼方程的解。

乘客感知时间与拥挤的关系为

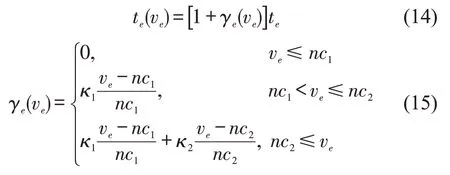
式中：γe(ve)为弧段e 的拥挤系数；te为列车实际运行时间；κ1、κ2为拥挤效应修正参数；n 为列车编组辆数；c1和c2分别为车辆的座位数和定员。由式(15)可知，拥挤系数是随流量的单调递增函数。弧段服务频率fe与该弧段所属的轨道交通线路的服务频率相等。

3.3 基于Logit模型的乘客路径选择模型

令ℋp表示连接o 和d 的超路径(即基本路径集合)，λl表示在ℋp中选择基本路径l 的概率。对于ℋp，需要确定各基本路径l的流量分配方法。令Qp为超路径ℋp的流量，ql为基本路径l ∈ℋp的流量，则有

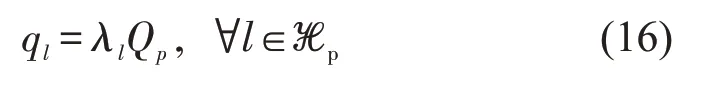
由式(16)可得基本路径l 上的弧段eij的流量ueij,l为

式中：当弧段eij∈l 时μeij,l=1，否则μeij,l=0。综上，弧段eij的总流量ueij为所有基本路径弧段流量ueij,l之和，即超路径的流量分配中，关键在于确定路径选择概率λ∙l，本文采用Logit模型计算λ∙l，即

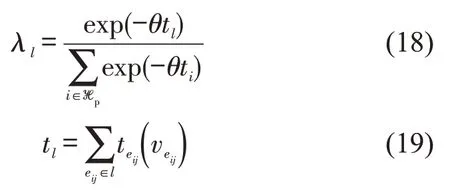
式中：θ 为非负参数；tl为基本路径l 的阻抗。以图6 所示超路径为例，假定3 条基本路径的选择概率分别为以弧段ei2i3为例，令Qp=6，则。

3.4 求解算法

增量分配法的思路是：首先将OD 需求分割成K 份，然后分K 次使用最短路分配方法，每次分配一份OD需求，每分配完一次后，路阻更新一次，直至把K 份OD 需求全部分配到网络上。与传统增量分配法有所不同，本文提出的方法在分配每一份OD需求时，采用基于Logit模型的最短超路径分配方法。客流增量分配算法以及最短超路径的求解算法具体如下。

(1)客流增量分配算法

基于超路径客流增量分配方法的算法步骤如下：

Step1 初始化。分割OD需求，即第k 份需求Qk=ωkQp，ωk为第k 份OD 需求的分配比例。令k=1，te(ve)=te(0)。

Step 2用最短超路径求解算法获得任意OD对间的最短超路径，并运用基于Logit 模型的乘客路径选择模型，将第k 份OD需求Qk分配至服务网络上。

Step 3更新网络弧段阻抗，根据式(14)和式(15)计算并更新弧段阻抗。

Step 4终止判断。若k=K ，则计算结束；否则，令k=k+1，返回Step 1。

(2)最短超路径求解算法

求解轨道交通服务网络中的最短超路径，即可得到有效路径。对轨道交通服务网络G，求解任意OD对之间的最短超路径需要任意OD对之间的子服务网络G′，故首先需要从全网络G 中提取出子网络G′ ，然后再将子网络输入SFT(Shortest Forward Tree,SFT)算法中求解最短超路径。根据算法需求，服务网络G 采用关联矩阵方式存储。具体算法步骤如下。

Step 1初始化。输入轨道交通服务网络G ，包括关联矩阵H 和节点集合E、列车在弧段的运行时间te和服务频率fe。

Step 2提取子网络。针对服务网络G 中任意车站节点OD 对(i,d)，提取出子网络G′相关信息(H′、E′和等)；

Step 3用SFT 算法计算任意车站节点OD 对(i,d)间的最短超路径。SFT算法步骤如下：

Step 3.1 初始化。令任意τ(i)=∞(i ≠d)和τ(d)=0；节点的前驱弧段集合Pe=∅，弧段的前驱节点集合Pv=∅；当前节点j=d。

Step 3.2迭代计算。计算节点j 的向后星令对每一条边et,j∈Et,j对应的尾节点nt,j∈Nt,j，若 τ(nt,j)>τ(j)+w ，则Pe(et,j)=j，Pv(nt,j)=et,j，τ(nt,j)=τ(j)+w。

Step 3.3更新节点集合和当前节点j 。即取出集合中标号最小的节点。

Step 3.4终止计算判断。若≠∅，则返回Step 3.2；若=∅，则终止计算。

Step 4输出结果。根据Pe和Pv回溯输出车站节点OD对(i,d)间的最短超路径，以及期望出行时间τ(i)，∙∀i ∈。

上述算法中，Nt,j和Et,j为节点j 的向后星中的尾节点集合和弧段集合。需要注意的是，从网络G中提取出子网络G′后，需要对子网络的关联矩阵H′、中的节点以及弧段集合E′的标号重新编号，以便在SFT算法中应用。在根据子网络求得最短超路径后，再将路径映射到原图G 中输出。

4 算例研究

4.1 算例及参数

以图1(a)所示多交路共线运营线路为例，该线路共有6 个车站，3 条交路，各交路服务频率fi=10 对⋅h-1,i=1,2,3(发车比例为1∶1∶1)。服务网络如图5 所示，共含20 个节点，33 条弧。列车编组(n1,n2,n3)=(4, 4, 4)；车辆座位数c1=31 个⋅辆-1，车辆定员c2=310 人⋅辆-1；拥挤感知参数κ1=1，κ2=2；乘客直达列车偏好概率取值为0，Logit模型参数θ=0.02，增量分配算法中采用非均匀分割，分割次数K =50 次，分割比例k=1,…,K (保留4位有效数字)。各弧段时间为：乘车弧时间如图5 所示，共线运营乘车弧时间相等，如te3=te5=8 min ；候车弧时间tei=0.5 min,ei∈∙j ∈Ns；下车弧时间车站客流需求为Qid=3500人次(i ≠d且∀i,d ∈Ns)。

4.2 结果分析

基于发车频率和乘客出行区段划分的分配方法(方法1)和基于超路径的客流增量分配方法(方法2)的配流结果如图7 所示，圆圈内数字表示服务网络节点标号，弧段上的数字为配流结果。由图7(a)可知，交路1和交路2在前两个断面(车站20～15、车站15～14)上分担的客流量与运能匹配较好。总体上看，各交路分担的客流量呈现了较大的不均衡性，交路1 的直达列车分担的客流更多。对比图7(b)可知，共线交路分担的客流量较为均衡，与运能匹配较好。

图7 两种方法的配流结果(流量×103)Fig.7 Assignment results of two methods(flow×103)

表1 为单一编组开行方案下两种配流结果的断面满载率。可以看出，方法1的断面满载率最高达141.1%(交路1 的断面4)，断面满载率差值最大为84.7%(断面3)，满载率极度不均衡；方法2 的断面满载率最高为113.1%，断面满载率差值最大为7.1%(断面3)，其他断面满载率差值均小于1%，满载率非常均衡。

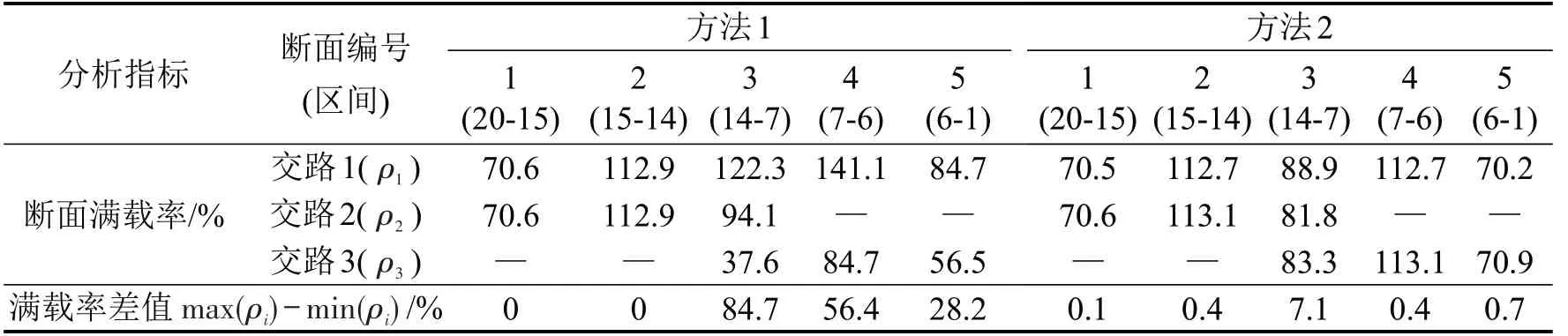
表1 单一编组模式下的断面满载率对比Table 1 Comparison of load factors for uniform train formation

5 结论

本文以城市轨道交通共线运营多交路为例，构建了基于发车频率和乘客出行区段划分的客流分配方法和基于超路径的客流增量分配方法，并设计算例研究了两种客流分配方法的有效性。研究结果表明：基于发车频率和乘客出行区段划分的客流分配方法是一种非均衡配流方法，适用于典型共线运营多交路形式和非拥挤条件下的客流分配，其突出优点是求解速度快；基于超路径的客流增量分配方法通过将多交路物理网络转化为共线运营服务网络，构建基于服务网络的客流增量分配方法。该方法可以适应多交路与快慢车、多交路与多编组等组合运营模式的客流分配，具有良好的适用性和可拓展性。后续研究的重点是模型中参数的取值及其灵敏度分析，以及客流拥挤感知刻画等因素对客流分配结果的影响。