基于双层规划的城市交通拥塞疏导优化研究

胡立伟，赵雪亭，杨锦青，张苏航，范仔健，殷秀芬，郭治

(昆明理工大学，交通工程学院，昆明650500)

0 引言

近几年，二线、三线城市不断发展，交通拥塞日益严重，已快速进入“拥挤的时代”。由交通拥塞引发的经济、社会、民生等一系列问题，严重制约城市的可持续发展。当城市路网中已经产生了交通拥塞，往往需要对路网进行区域交通信号控制。而合理的交通小区划分和交通拥塞疏导优化能够提高区域信号协调控制的效率和效果，是区域信号协调控制的基础。

目前国内外学者对交通小区划分、交通拥塞控制进行了大量的研究。利用路网宏观基本图特性对交通子区进行划分和边界控制，使得子区内部交通拥塞情况得到一定的缓解，但其没有考虑交通子区外的交通运行状态对子区内部及边界上车辆的影响，路网整体运行效果达不到最优状态[1-3]。Daganzo 等通过保持信号绿红比不变的简单规则来动态调整信号偏移量以达到缓解交通拥堵的目的[4]。Batista等基于宏观基本图研究行程长度对区域动态模型精度的影响[5]。Anderson等基于宏观基本图研究动态公交车道政策的影响[6]。别一鸣对交通子区划分现状进行详细的综述，并提出交通子区动态划分策略，对交通子区划分方法和关联度模型的构建具有一定的指导意义[7]。卢守峰等将路网连接性融入算法解决了非均质路网交通子区划分的不足[8]。曲大义在前人研究的基础上充分考虑车辆离散性、阻滞性和交通流特征等因素对交叉口关联度的影响，通过聚类分析方法对交叉口群进行划分[9]。

交叉口关联度的计算是交通小区划分的核心和基础。然而，许多学者在交叉口关联度模型适用范围上较为粗略，没有根据路网的具体运行状态进行细化，考虑因素不够全面。且对区域路网进行边界控制时，虽然子区内部路网交通拥塞情况有了一定的缓解，但是边界上交叉口却异常拥堵，控制效果并不理想。因此，本文对关联度模型的应用进行细化，并在此基础上将交通拥塞控制区划分为“疏散区”“平衡区”，同时根据两区不同控制目标，将双层规划理论应用于城市交通拥塞研究，并建立基于双层规划理论的城市交通拥塞疏导优化模型，以为交通拥塞治理提供参考。

1 交通拥塞控制子区划分方法研究

1.1 模型基础

对交通拥塞控制子区进行划分，首先要明确子区划分的影响因素，并建立相邻交叉口关联度模型。许多学者对影响交叉口之间关联度的主要因素进行了总结，主要分为动态和静态因素，包括交通流量、信号周期、绿信比、车辆离散特性、交叉口间距等，通常采用美国交通控制手册中的Whitson模型以及它的改进模型来计算交叉口之间的关联度，其计算公式为

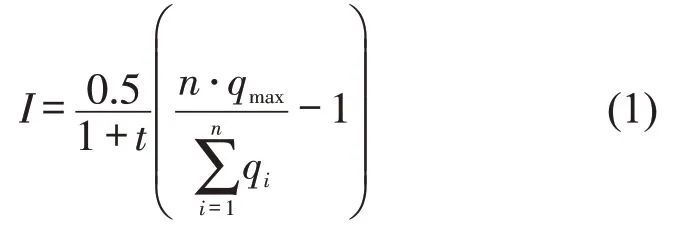
式中：I 为相邻交叉口之间路段关联度；t 为上游驶向下游交叉口的平均行驶时间；qmax为上游流向下游交叉口流量流向中的最大流量；n 为上游流向下游交叉口的流向数；为上游流向下游交叉口交通流量总和，其中，qi为上游流向下游交叉口的交通流量，i 为上游流向下游交叉口的流向数的起始值为1。

1.2 关联度模型构建

当城市区域路网运行呈现饱和或过饱和状态时，路口车辆等待排队特征较为明显，排队长度蔓延至其他交叉口严重情况下会造成交通锁死。而式(1)未考虑路段排队情况，主要应用于欠饱和情况下交叉口之间关联度的研究。排队数能反映交叉口的运行状态，同时可体现交叉口协调控制，因此当交叉口处于饱和或过饱和状态时可定义交叉口之间的关联度为道路实际排队数与阻塞排队车辆数之比[10]。即当路网中交叉口属于欠饱和状态时，用式(1)计算交叉口和路段之间的关联度，而当交叉口属于饱和或过饱和状态时则采用排队关联度进行计算。交叉口关联度计算模型为

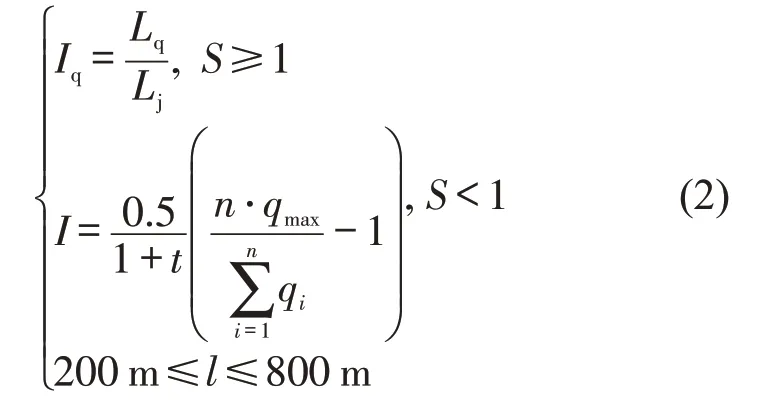
式中：Iq为交叉口之间的关联度；Lq为排队车辆数；Lj为阻塞排队车辆数，由路段长度l，车道数m和阻塞密度kJ确定，LJ=l ⋅kJ⋅m；S 为交叉口或路段的饱和度。当S ≥1 时，即为饱和或过饱和状态；当S<1 时，为欠饱和状态，对交叉口饱和度的识别可通过文献[11]获得。

1.3 交通拥塞控制子区划分方法研究

结合关联度模型，将交通拥塞控制区分为两部分，即“疏散区”“平衡区”。“疏散区”是指那些交通运行状态处于饱和或过饱和下的相互关联交叉口及路段的集合，该路网区域急需进行快速疏导，实现交通流的最大化输出。“平衡区”是指从“疏散区”边界路段出发沿疏散区主要交通流汇集方向和疏散方向扩展的路段和交叉口的集合，该路网区域主要对“疏散区”内疏散的交通流起到缓冲作用，可通过控制边界交叉口抑制其他交通流进入拥堵控制区域，实现疏散区和平衡区内交通流均衡分布。交通拥塞控制子区划分示意如图1所示。

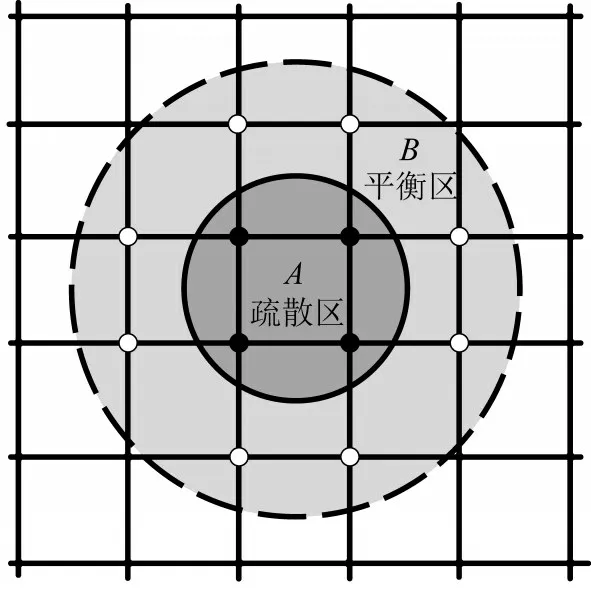
图1 交通拥塞控制子区划分示意Fig.1 Schematic diagram of traffic congestion control sub-areas

首先，为了提高控制子区划分的高效性及稳定性，借助python软件对高德地图进行早晚高峰实时路况数据爬取，对城市区域路网进行拥塞初始识别定位，其次在划分算法运行之前将路网内交通运行畅通、轻度拥塞的交叉口和路段进行筛选，初步确定需要进行协调控制的基本范围。为此本文采用拥堵延时指数表征道路交通运行状态，公式为

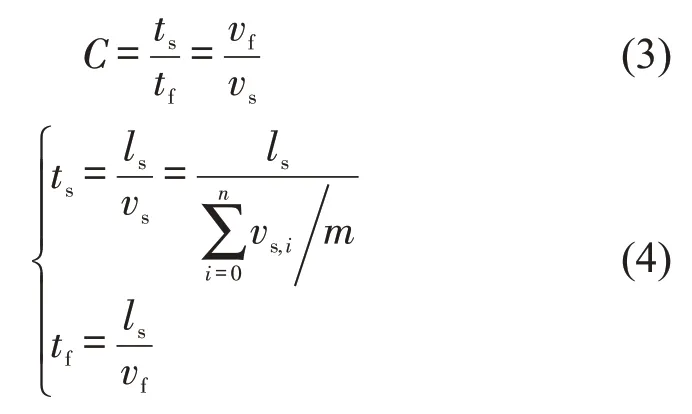
式中：C 为拥堵延时指数；ts为实际出行时间；tf为自由流情况下出行时间；vs为车流的实际行程速度；vf为车辆自由流车速；vs,i为第i 辆车的平均行驶速度；ls为道路的实际长度；m 为路段中的车辆数。

根据高德地图交通运行状态判断交通拥塞程度，当0 ≤C<1.5 时为畅通，1.5 ≤C<2.0 为缓行，2.0 ≤C<4.0 为拥塞，C ≥4.0 为严重拥塞。在交通拥塞控制子区算法运行之前，通过该判断标准将C值小于1.5的路段和交叉口删除，对路网进行简化，确定初始控制范围。同时为保证交通子区划分稳定性，交通子区划分方案规定执行10～15 min 后进行方案更新切换。划分交通拥塞控制子区的步骤如下。

(1)“疏散区”划分方法

根据“疏散区”的定义，采用式(2)中排队关联度模型进行计算，当两个相连交叉口关联度值Iq大于判别阀值θ1，并且两个相连交叉口和路段之间的长度在200～800 m时，将其划入“疏散区”。当相邻的疏散区A1、A2和A3边界有所重合，可将疏散区合并为A4，此时新组合的A4内部区域包括A1、A2和A3的内部区域以及重合的路段，而A4的外部边界则由A1、A2和A3的边界路段且除去重合的路段组成。A1、A2和A3合并为A4的演化过程如图2所示。

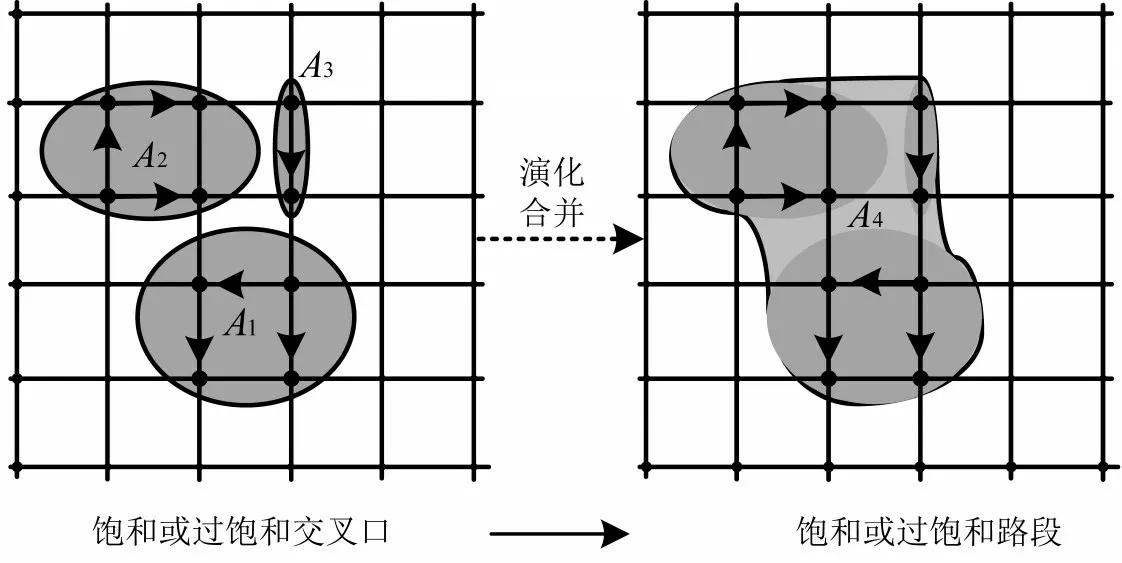
图2 交通拥塞控制子区合并示意图Fig.2 Schematic diagram of merging traffic congestion control sub-areas

(2)“平衡区”划分方法

根据“平衡区”的定义，疏散区边界路段出发沿疏散区主要交通流汇集方向和疏散方向扩展是“平衡区”的划分范围。相较“疏散区”而言，“平衡区”交通运行则为欠饱和状态，可根据式(1)关联度模型进行求解，当关联度值I 大于判别阀值θ2，且路段长度l ∈[2 00,800] m，划入“平衡区”。同时为防止“平衡区”划分范围过大，规定“平衡区”最多包括三级上下游关联交叉口。同理，当平衡区存在重叠时，可将其合并。

城市路网中发生区域性交通拥塞时，应对交通拥塞辐射影响范围内交叉口群进行整体的信号配时优化。首先，通过交通拥堵延时指数对C 值小于1.5 的路段和个别孤立交叉口进行筛选，初步确定拥塞控制范围；其次，基于关联度模型将拥塞控制区划分为“疏散区”“平衡区”。交通拥塞子区划分后应确定路网优化目标，针对性地提出交通疏导控制策略，并将在交通子区划分方法的基础上建立基于双层规划理论的交通拥塞疏导优化模型。

2 城市路网交通拥塞疏导优化模型研究

2.1 模型基础

交通拥塞的治理是一个多目标优化问题，包括排队长度最小、通行能力最大、平均延误时间最小等，且各目标间有时存在互相矛盾的情况。优化这些目标就是在各目标间寻求一种平衡关系使得利益最大化。双层规划模型是一种具有双层递阶结构的系统优化问题，上、下层问题都有各自的目标函数和约束条件。其一般表达形式为

式中：x 为上层决策变量；y 为下层决策变量；F(x,y)为上层目标函数；G(x,y)为上层约束条件；f(x,y)为下层目标函数；g(x,y)≤0 为下层约束条件。

第1节中将交通拥塞子区划分为“疏散区”“平衡区”，两区之间相互影响，同时拥塞控制策略主要以疏散区内交通拥塞快速疏散为主，平衡区内交通分布均衡为辅。通过对拥塞控制子区进行划分建立基于双层规划理论的城市区域路网交通拥塞疏导模型。

2.2 上层规划模型

上层规划模型的目标以疏散区交通拥塞快速疏散为主，即在控制时段内对疏散区A 的边界交叉口进行控制使得A 内交通流量输出最大化。上层规划模型的决策变量为疏散区A 的有效绿灯时间，对模型决策变量进行约束，疏散区A 边界交叉口i的各相位有效绿灯时间需在最小绿灯时间gmin和最大绿灯时间gmax之间。周期时长Ci为各边界交叉口i 的各相位有效绿灯时长与周期损失时间Li之和。且下游交叉口各相位的有效绿灯时间与对应的车道饱和流率之积要大于上游交叉口，这样才能保证实现交通流的快速疏散。同时为防止交叉口排队溢出，交叉口各车道上的排队车数要小于最大车道的排队车数。经过上述分析，构建上层规划模型的目标函数及约束变量为

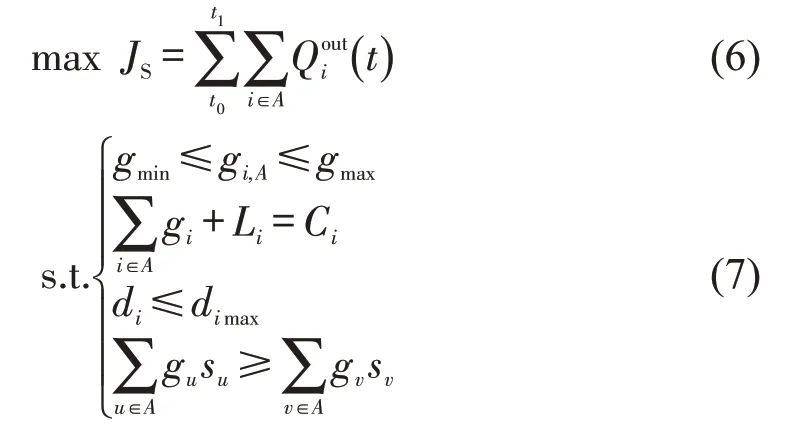
式中：JS为疏散区A 在控制时段内输出的交通量；t0、t1分别为控制时段的开始和结束时间；i 为疏散区A 的第i 个边界交叉口；为第i 个交叉口在有效绿灯时间gi内交通输出量，可结合路网宏观基本图特性进行求解；gi,A为疏散区A 的第i 个边界交叉口的有效绿灯时间；Li为交叉口i 的总损失时间；gi为交叉口i 各相位有效绿灯时间；Ci为交叉口i 的信号周期；di为交叉口i 的各车道排队长度；dimax为最大车道排队长度；gu、su分别为下游交叉口u 的各相位有效绿灯时间和对应的车道饱和流率；gv、sv为上游交叉口v 的各相位有效绿灯时间和对应的车道饱和流率。

2.3 下层规划模型

下层规划模型则针对疏散区和平衡区的整体协调控制为主，以交通流均衡分布为目标，即实现疏散区A 和平衡区B 内各路段的车辆占有率最小且较为相近。下层规划函数以车辆排队长度为决策变量，除有效绿灯时间与周期时长满足相应的约束外，为防止车流排队溢出，疏散区A 和平衡区内B 所有路段上的车辆排队数均要小于对应各车道上的最大排队数。构建下层规划和约束条件为

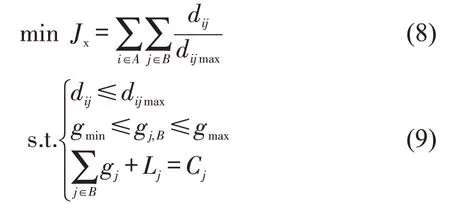
式中：Jx为疏散区A 和平衡区B 内各路段的车辆占有率；dij为A 和B 内各路段上的车辆排队数；dijmax为对应最大车道排队数；gj为第j 个交叉口在有效绿灯时间；gj,B为平衡区B 内交叉口j 各相位的有效绿灯时间；Lj为周期损失时间；Cj为周期时长。

2.4 模型求解

双层规划模型属于多目标约束函数模型，参考文献[12]的遗传算法求解，具体过程如下：

(1)初始化上层规划种群GA并使其满足约束条件，分别设定上、下层规划函数迭代次数为Ns和Nx，规模大小为Ms、Mx。

(2)将上层个体带入下层规划，初始化下层种群dij，利用宏观交通仿真检验种群dij是否满足约束条件，满足则进入第(2)步，不满足则返回第(1)步。

(3)求解下层规划目标函数值，并进行适应度评价，其中适应度函数选择式(6)～式(9)分别作为上下层遗传算法目标函数。对下层规划的适应度评价结果进行交叉、变异，其中交叉概率为Pxj、变异概率为pxb，参数可通过经验取值确定，得到最优值后返回上层规划模型中。

(4)求解上层规划函数并进行适应度评价，进行交叉、变异，其中交叉概率为Psj、变异概率为psb，并将变异后的种群作为新一代种群。

(5)当上层迭代次数达到设定的最大迭代次数Nx时，终止运算；否则利用遗传算法对上层决策种群进行选择、交叉、变异后返回第(2)步。

3 算例分析

本文选取昆明市部分城市路网作为实验对象，通过VISSIM 对路网进行交通运行仿真，将实际控制方案与本文模型计算方案的控制效果进行对比，以此验证模型的适用和有效性。选取路网包含34个交叉口，136条路段，并根据实际调查情况设定交通流转向比例、大车小车比例、信号配时等参数，区域路网结构简图如图3 所示。根据关联度计算模型及交通拥塞控制子区划分方法对路网进行划分，交通控制子区划分方案执行15 min 后进行方案更新切换。其次，根据疏导优化模型目标函数及控制策略借助MATLAB 对模型进行数值模拟，将本文的设计方案进行交通运行仿真。仿真结束统计各方案控制效果对比如图4～图6和表1所示。

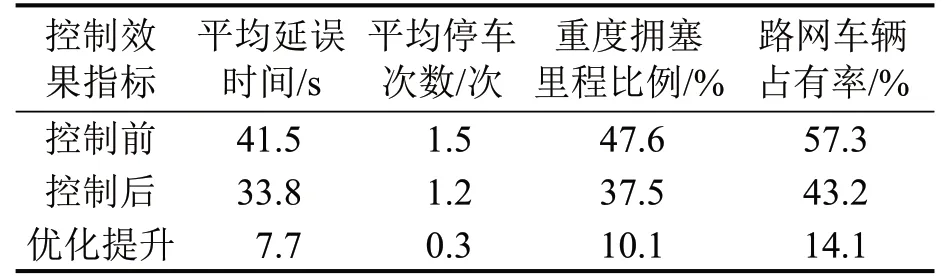
表1 仿真过程控制效果指标平均值对比Table 1 Comparison of average value of simulation process control effect index

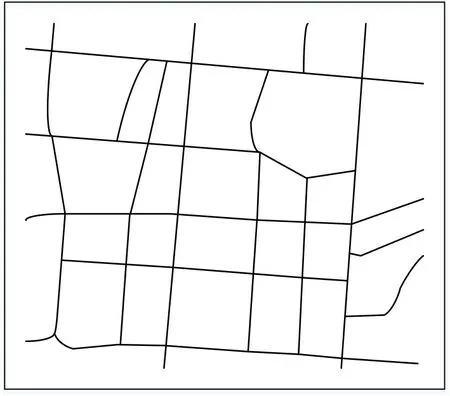
图3 路网简图示意Fig.3 Schematic diagram of road Network

由图4 可知，在1800 s 之前两个方案控制下的车辆平均延误时间相差不大，1800 s以后至仿真结束，本文设计方案的车辆平均延误时间始终在实际控制方案之下，而车辆的平均停车次数在整个仿真过程中始终低于实际控制方案，表明本文设计的方案能有效降低车辆延误时间、减少平均停车次数，提升路网服务水平。由图5 及图6 可知，在路网运行初期，随着交通流量的加载，路网中拥堵里程比例及车辆占有率均升高，实际控制方案下仿真时长为5400 s 时，路网拥堵里程达到最大为69%，仿真结束时为65%，而本文设计方案进行控制下重度拥堵里程比例最高为52%，仿真结束时为41%。路网的车辆占有率与拥塞里程比例是相关的，通过本文设计方案，路网车辆占有率维持在50%左右，避免了车辆的高密度聚集，使得交通拥塞控制子区内车辆较实际控制方案之下，车流分布要更加均衡。

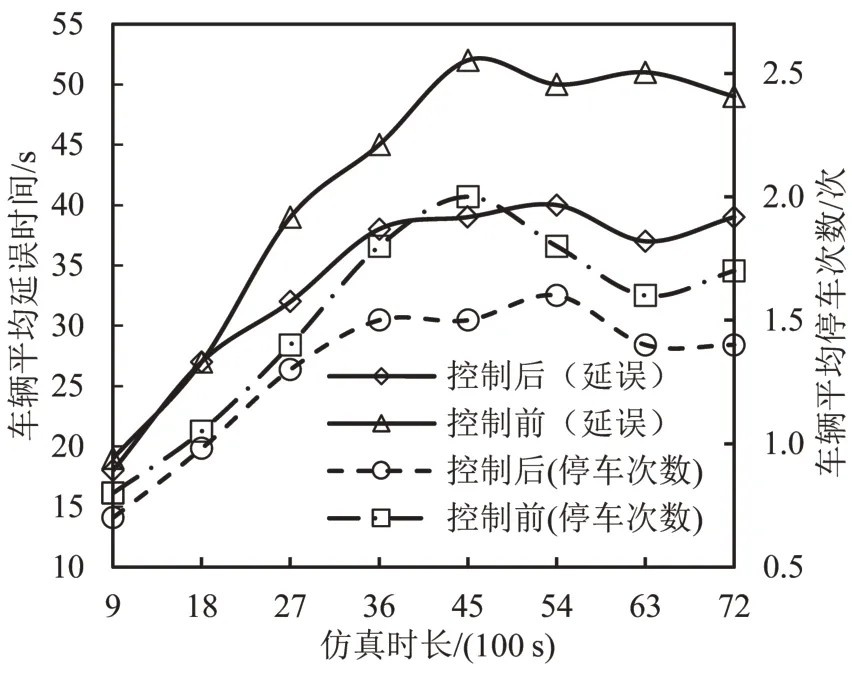
图4 控制前后延误与停车次数对比Fig.4 Comparison of delays and stop times before and after control

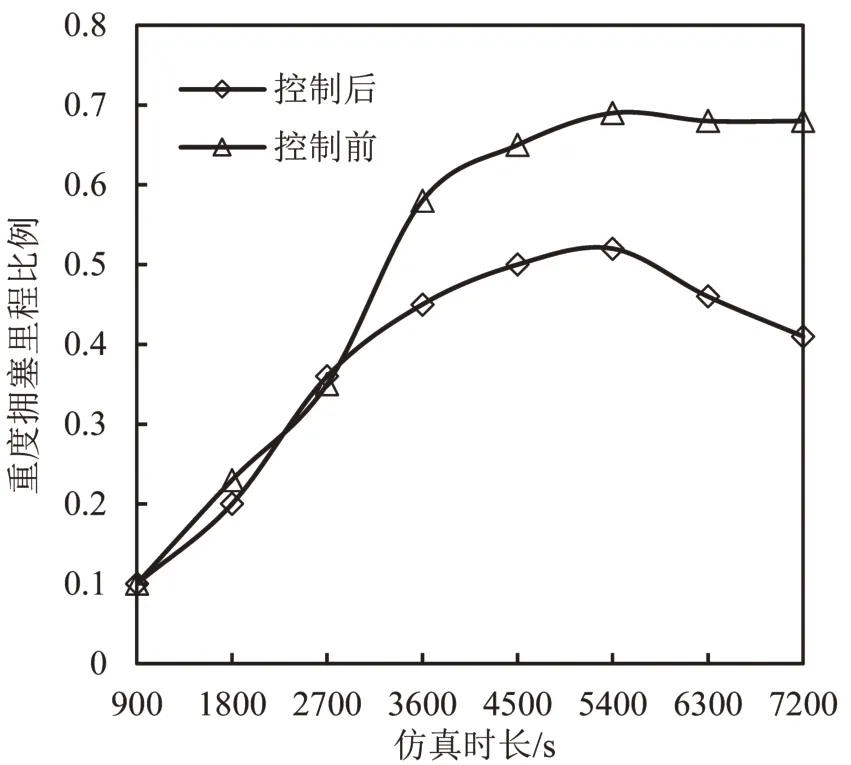
图5 控制前后重度拥塞里程比例对比Fig.5 Comparison of proportion of severely congested mileage before and after control

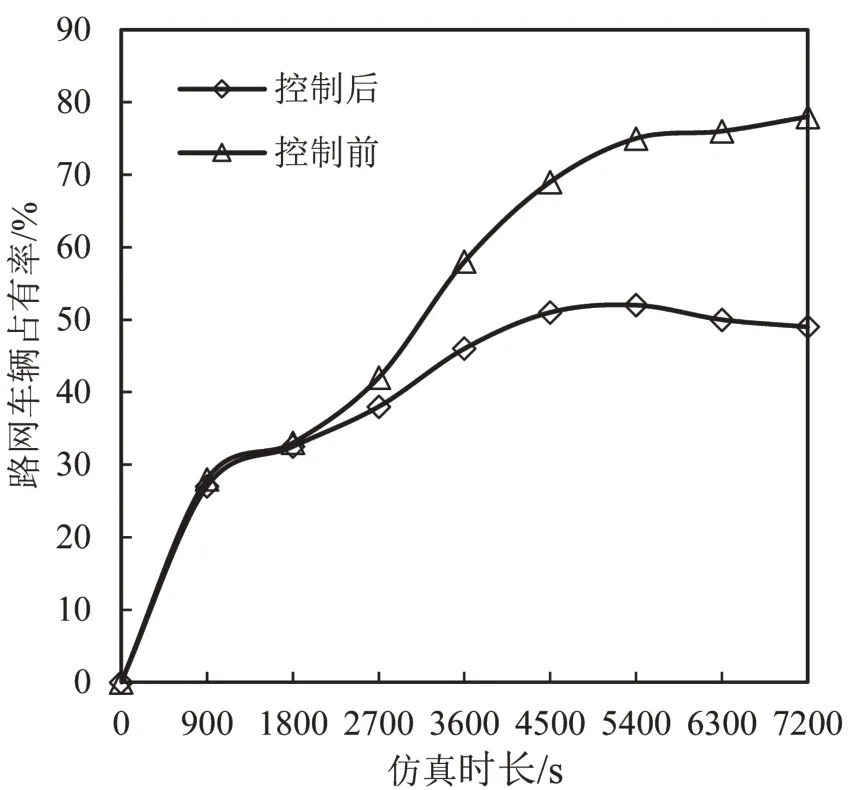
图6 控制前后路网车辆占有率对比Fig.6 Comparison of vehicle occupancy rates in road network before and after control

由表1可知，除平均停车次数优化效果一般以外，其他控制效果指标均具有很大的优化提升，其中车辆平均延误时间降低了7.7 s、重度拥塞里程比例下降了10.1%，路网车辆占有率下降了14.1%。综上可知，本文疏导优化模型控制可快速疏导和有效缓解交通拥塞，模型具有良好的有效性，可为路网交通拥塞分区治理及疏导控制提供参考。

4 结论

城市路网中发生区域性交通拥塞时，应对交通拥塞辐射影响范围内交叉口群进行整体的信号配时优化以缓解交通拥塞。为此，本文将双层规划理论应用于城市交通拥塞控制研究，以在控制时段内“疏散区”的交通流量输出最大化、“疏散区”“平衡区”的交通流均衡分布为目标，建立了基于交叉口关联度模型并考虑交通子区划分的城市交通拥塞疏导控制模型，为城市交通管理者提供了新的控制思路。

研究结果表明，通过模型计算的交叉口控制方案能有效降低车辆延误时间、减少平均停车次数、降低重度拥塞里程比例、降低路网车辆占有率，提升路网服务水平。在城市交通拥塞区域对交叉口实施根据模型计算的控制方案具备一定的可行性。

本文提出的交叉口控制方案可缓解交叉口拥塞问题，但还仍需对交通拥塞区域进行细化，例如考虑不同类型的交叉口并结合信号控制系统对控制方案进行调整是下一步的研究重点。