地铁网络服务韧性评估与最优恢复策略
2021-10-30吕彪管心怡高自强
吕彪,管心怡,高自强
(1.西南交通大学,信息科学与技术学院,成都611756;2.四川省列车运行控制技术工程研究中心,成都611756)
0 引言
以地铁网络为主要代表的城市轨道交通网络在日常运营中不可避免会受到诸如设备故障、自然灾害和蓄意攻击等扰动事件影响。为评价扰动事件下路网运行稳定性,传统做法是以可靠性、鲁棒性为测度指标评估路网维持预期服务水平的能力或以脆弱性为测度指标衡量路网可能遭受的不利影响。例如,刘志谦等[1]采用Space L方法进行拓扑建模,研究了广州轨道交通网络换乘车站故障情况下路网受影响程度及可靠性;Zhang 等[2]评估了上海地铁网络的可靠性和鲁棒性;孙杨等[3]提出不确定需求下轨道交通网络的鲁棒性优化方法;肖雪梅等[4]以满足乘客出行为目标建立了城轨路网连通可靠度评估模型;刘杰等[5]以区间能力失效前后乘客的广义出行费用确定乘客的出行是否可靠;叶青[6]以重庆轨道交通网络为例计算了各站点对蓄意攻击的脆弱性;Sun 等[7]提出基于换乘和客流的地铁脆弱性评价模型;Zhang 等[8]对地铁网络进行了基于连通性和功能性的脆弱性研究。随着研究不断深入,研究者逐步意识到,由于扰动事件难以避免,可靠性与脆弱性指标均存在不足。因为运营管理者和乘客不仅关心扰动后路网保持正常状态的概率或遭受不利影响的程度,同时更关心一旦路网偏离正常状态后如何快速恢复到预期状态。在此背景下,学者开始使用韧性作为扰动事件下交通网络性能测度指标。所谓韧性,尽管不同学科领域定义有所不同,但其核心内涵包括两方面:一是系统抵御扰动的能力,通过扰动后系统偏离正常性能的程度体现;二是系统快速恢复到预期状态的能力[9-10]。Murray-Tuite[11]首次提出交通系统韧性的概念和量化方法。Zhang等[12]以拓扑效率为路网性能指标,以扰动事件后路网性能损失程度为韧性指标,并以排列组合方式确定失效单元恢复次序;张洁斐等[13]以拓扑效率为路网性能指标,以扰动事件后路网拓扑效率累积损失程度为韧性指标,提出基于韧性评估的地铁网络修复时序方案。
综合来看,关于地铁网络韧性的研究尚处于起步阶段,成果十分有限。文献[12-13]构建了地铁网络韧性评估基本框架和单元失效基本恢复策略,但存在以下不足:①以拓扑效率为路网性能指标,将地铁物理网络等价于服务网络,不符合地铁运营实际。地铁服务网络以列车开行计划为基础,现实条件下由于跨线运行条件、信号设备制式等限制,单一节点失效很可能会造成该节点所在线路列车停运,使得从拓扑结构上保持连通的两节点间无法提供运输服务。②提出的随机恢复、偏好恢复等策略均为经验性恢复策略,当扰动事件造成多个单元失效时,很可能遗漏最优方案,仅得到次优甚至严重偏离预期的方案。
为弥补已有研究不足,本文从地铁运营实际出发,定义服务效率为路网性能指标,构建基于服务效率的路网韧性评估模型,提出了以路网服务韧性最大化为目标的最优恢复策略。
1 地铁网络韧性评估模型
1.1 地铁网络韧性的定性描述
扰动事件下地铁网络性能变化如图1 所示。图中,t0,te分别表示扰动前某特定时刻、扰动事件e 发生时刻;tr1,tr2分别表示采用恢复方案1、2的路网性能恢复时刻。扰动事件下地铁网络性能变化可划分为3个阶段,即未发生扰动阶段(te以前)、扰动持续影响阶段(te至tr1或te至tr2)、扰动影响消除阶段(tr1或tr2以后)。 F(t0), F(te), F(tr1) , F(tr2)分别表示t0,te,tr1,tr2时刻的路网性能。如前所述,韧性核心内涵包括两方面:一是路网抵御扰动的能力,通过扰动后路网性能退化程度体现;二是路网从扰动中恢复的能力,通过路网恢复速度和恢复程度体现。根据这一界定,通过扰动后路网性能累积损失程度描述路网韧性[12-13]。
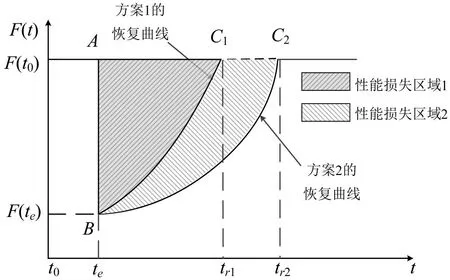
图1 地铁网络韧性的图解表示Fig.1 Graphical representation of metro network resilience
显然,恢复策略对地铁网络韧性产生直接影响。假设以效率作为地铁网络性能指标,未发生扰动事件时地铁性能稳定,t0时刻路网效率为F(t0);当te时刻扰动事件发生,路网效率下降至F()te;为恢复路网性能,可采取两种方案。方案1耗费资源数量多,但恢复速度快,tr1时刻即可恢复至扰动前水平,路网整体性能损失为ABC1围成区域的面积;方案2 耗费资源少,但恢复速度慢,tr2时刻才可恢复至扰动前水平,路网整体性能损失为ABC2围成区域的面积。比较来看:方案1 恢复速度快、路网性能损失小,得到的路网韧性高;方案2 恢复速度慢、路网性能损失大,得到的路网韧性低。
1.2 地铁网络性能指标
要确定路网韧性,首先要确定路网性能指标。与已有研究[12-13]一样,运用Space L方法建立路网拓扑结构。将地铁网络抽象为由节点和边构成的无向无权图,其中,节点表示地铁车站,边表示站间线路。如果两站间存在线路直接相连,则两节点间存在一条边相连。令G=(V ,E)表示地铁网络,其中,V 为节点集,V={1 ,2,…,N },N 为节点数量;E 为边集,E={eij|i ∈V,j ∈V,i ≠j} ,其中,eij表示节点i与j 之间的边。令A=(aij)N×N表示邻接矩阵,若节点i,j 之间存在一条直接相连的边,aij=1;否则,aij=0。已有研究[12-13]普遍基于复杂网络理论,使用拓扑效率作为路网性能指标。路网拓扑效率表示为路网所有节点对效率的平均值,其中节点对效率反映从一个节点到达另一个节点的难易程度,通常表示为节点间距离的倒数。令φ()G 表示路网G 的拓扑效率,可表示[14]为
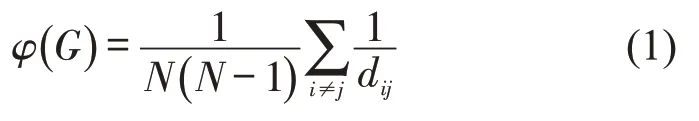
式中:dij为节点i,j 之间的最短拓扑距离,即从节点i 到节点j 所需经过的最小边数。
式(1)从拓扑结构上直观反映了地铁网络物理设施间的连接关系和站点间的流动难易程度。然而,评价地铁等城市轨道交通网络性能时,不能单纯考虑拓扑结构,应当考虑交通流的影响,否则可能误判路网性能[15-22]。例如,冯佳等[18]在研究城市轨道交通网络复杂性时以断面客流量为站间线路权重,揭示客流分布呈现明显幂律分布特征,指出明晰交通流时空分布、耦合关系、演化模式等特征,是城市轨道交通网络复杂性建模分析的重要前提。此外,需要指出的是,地铁物理设施网络与服务网络并非一一对应,换句话说,即使站点间存在连通路径,并不能保证实现站点间的乘客流动。这是因为地铁服务网络是以列车开行计划为基础的,现实中由于跨线运行条件、信号设备制式等差异,地铁列车无法实现跨线运行,甚至在同一条线路间除始终点站外无法折返运行。也就是说,当扰动事件导致某一站点失效,很可能导致该线路全线停运,事实上造成线路全部节点失效。基于上述分析,本文从地铁实际运营情况出发,提出一种基于流量加载的服务韧性指标。首先定义节点间服务效率,令φS,ij表示节点i,j 之间的服务效率,具体表示为
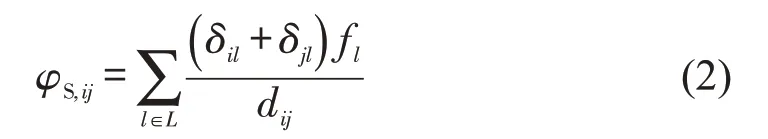
式中:L 为线路集合,L={1 ,2,…,M} ,M 为线路数量;fl为线路l 上的日均客流量;δil为0-1变量,如果节点i 在线路l 上,δil=1,否则δil=0。当扰动事件导致某一节点失效,途经该节点的线路列车停运,线路流量将变为0。
将路网服务效率表示为所有节点对服务效率的平均值,即
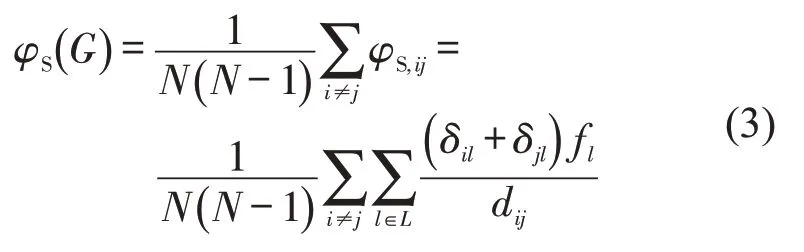
式中:φS(G)为路网G 的服务效率。可以看出,路网服务效率可反映扰动事件下地铁网络实际服务能力和效率。此外,从式(3)可以看出,不同节点承载的流量不同,对路网服务效率贡献程度亦不同。
为便于分析,将式(3)进行归一化处理,即
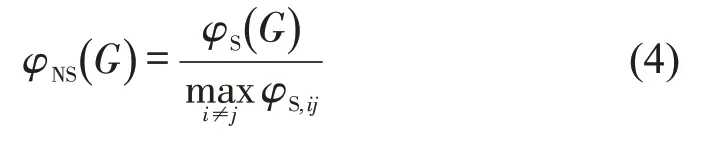
式中:φNS(G)为归一化的路网服务效率;为最大节点对服务效率。
1.3 路网服务韧性
在构建路网服务效率指标基础上,根据地铁网络韧性内涵界定,本文将路网服务韧性定义为扰动持续影响阶段路网服务效率与正常状态下路网服务效率的比值,即
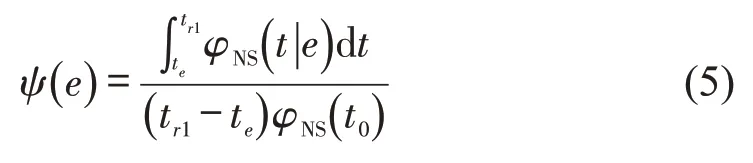
式中:ψ(e) 为扰动事件e 发生后采用恢复策略1时地铁网络服务韧性;φNS(t |e)为扰动事件e 发生后t时刻路网服务效率;φNS(t0)为正常状态下的路网服务效率。从式(5)可以看出,分子表示从扰动发生时刻到恢复时刻路网保留的累积性能,分母表示正常状态下同等时间长度路网的累积性能。直观来看,ψ(e)可表示为图1 中Btetr1C1围成的近似梯形区域面积与Atetr1C1围成的矩形区域面积的比值。
1.4 节点服务效率重要度
扰动发生后,为提升路网恢复能力,需要根据某种规则确定失效单元恢复先后次序,故需要设计相应指标以确定不同单元重要程度。本文提出基于服务效率的地铁网络节点重要度指标(Node Importance Based on Service Efficiency),以节点失效前后路网服务效率的相对变化反映节点重要程度。
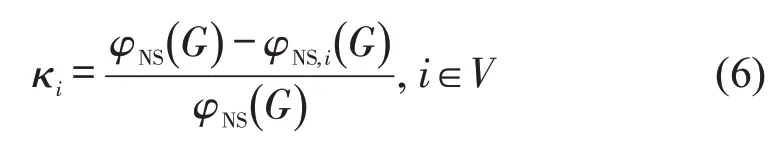
式中:κi为节点i 的服务效率重要度;φNS,i(G)为节点i 失效后路网G 的服务效率。
2 基于遗传算法的最优恢复策略
扰动事件造成节点或边失效后路网如何有效恢复到预期状态是韧性研究的核心问题。所谓节点失效,是指由于自然灾害、蓄意攻击、设备故障等原因造成车站物理设施损坏或丧失工作能力,以及运营管理存在安全隐患无法保证列车安全有效运行从而终止行车计划的状态。所谓节点恢复是指通过采用有效措施恢复车站物理设施正常功能和运营管理秩序,消除潜在安全隐患,使车站具备实施列车开行计划、提供正常运营服务能力的状态。
如图1 所示,面对相同扰动情景,不同恢复策略会得到不同路网韧性指标。已有研究主要使用穷举恢复[12]、随机恢复[13]、优先恢复[13,23]等策略确定失效单元恢复顺序。穷举恢复列出所有可能方案,逐一比选后确定最优方案,对于备选方案多的情形显然不适用;随机恢复为随机确定恢复次序,具有随意性和很大不确定性;优先恢复根据决策者主观偏好,基于某种准则(如节点度、单元重要度大小)确定恢复次序,这种策略优于随机恢复,但备选方案数量大时可能漏掉最优方案,仅得到次优方案。为弥补已有研究不足,本文提出基于韧性最大化的最优恢复策略。所谓最优恢复,是指通过建立优化模型,在所有可行方案中确定最优的失效节点恢复(节点所代表的车站具备实施列车开行计划、提供正常运营服务的能力)次序,从而实现路网服务韧性最大化。优化模型为
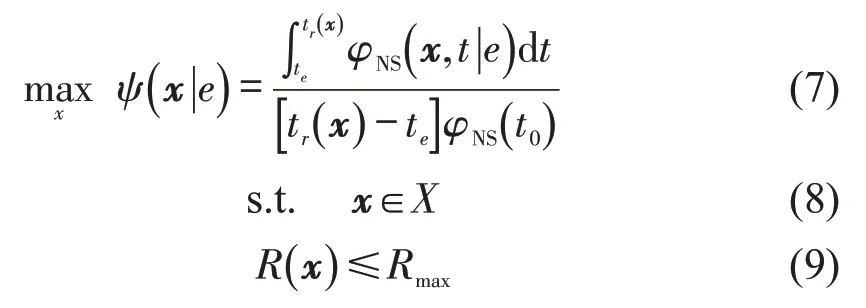
式中:x 为一种恢复方案,x=(… ,xj,…) ,xj为排序为j 的单元编号;tr(x)为采用方案x 时的路网恢复时间点;φNS(x, t |e)为扰动情景为e 采用方案x 时t 时刻的路网服务效率;X 为备选方案集合;R(x)为方案x 所需资源数量;Rmax为能提供的最大资源数量。
式(7)为优化目标,表示扰动情景为e 时路网韧性最大化。式(8)和式(9)为约束条件,式(8)中如x=(2,3,5,7,9,1,6,4,8)表示有9个待维修单元,按照单元2,3,5,7,9,1,6,4,8的次序维修,式(9)表示资源约束。
当备选方案数量较少时,可通过穷举并比较各种方案得出最优解,但当备选方案数量较大时,解空间规模呈指数级增长。例如,扰动事件导致10个节点失效,要确定这10个节点的恢复先后次序,可能的方案高达10!=3628800。当解空间规模庞大时,智能优化算法具有显著优势,因此本文利用遗传算法强大的并行计算能力、自适应能力和全局寻优能力求解模型。限于篇幅,算法步骤从略。
3 算例分析
以成都地铁为测试网络,拓扑结构如图2 所示。成都地铁共包括12 条线路,286 个站点,其中1,2,3,4,5,7,10号线已开通运营1年以上,客流量稳定,日均客流量分别为f1=88.54 万人次,f2=81.04 万人次,f3=70.77 万人次,f4=60.25 万人次,f5=34.45 万人次,f7=74.03 万人次,f10=7.92 万人次;6,8,9,17,18 号线尚处于初期运营或试运营阶段,无实测数据,假定日均客流量为60万人次。假设3 种扰动情景:情景1 为洪水倒灌致7 号线站点90,227,153,12,226,192,225,224,223,56失效;情景2为电力系统故障致10号线所有站点失效;情景3 为蓄意攻击致19, 22, 32, 44, 47, 82, 84, 88, 101,107,126,191等换乘站失效。令te=0,即扰动发生在0时刻。假定维修换乘站需要2 d,非换乘站需要1 d。遗传算法参数为:种群规模80,最大遗传代数100,交叉概率0.90,变异概率0.05。
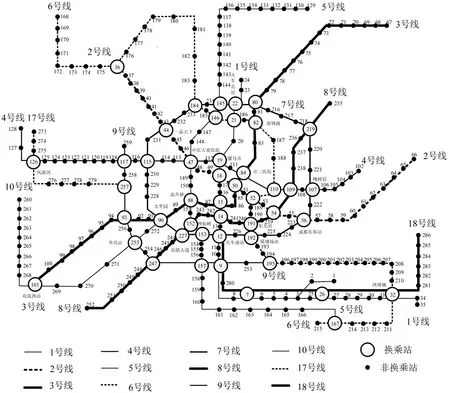
图2 成都地铁网络拓扑结构Fig.2 Topological diagram of Chengdu metro network
图3为遗传算法的收敛性。可以看出,算法在运行23 代后便收敛至最优目标值,说明遗传算法收敛性好,用于求解本文模型是可行的。
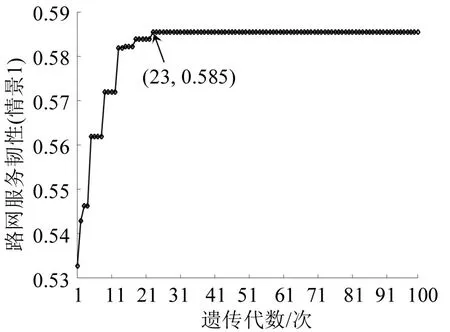
图3 遗传算法的收敛性Fig.3 Convergence of genetic algorithm
图4 为3 种扰动情景下,分别以服务效率和拓扑效率为测度指标得到的路网性能恢复曲线(假定受资源限制,只能同时恢复1 个节点)。可以看出,无论扰动情景如何,两种指标下路网性能恢复曲线明显不同。这是因为不同指标具有不同测度标准,会产生不同节点恢复优先次序。如表1 所示,3 种情景下分别以服务效率和拓扑效率为路网性能指标,得到的路网恢复策略明显不同。如发生情景3时,若以服务效率为路网性能指标,节点191 恢复次序排在第1 位;以拓扑效率为路网性能指标,节点191的恢复次序排在第10位。这一结果表明,应根据地铁实际运营特点,合理选择路网性能指标,否则可能得到次优恢复策略,无法实现预期目标。此外,不同扰动情景对路网性能潜在影响明显不同,蓄意攻击(情景3)造成的影响最大、破坏力最强。例如,正常状态时路网拓扑效率和服务效率分别为0.103 和0.037,发生扰动情景3 时路网拓扑效率和服务效率分别下降为0.052和0.001,仅为正常状态时的50.49%和2.70%。

表1 不同情景不同指标下节点恢复次序Table 1 Node recovery orders under different scenarios with different indicators
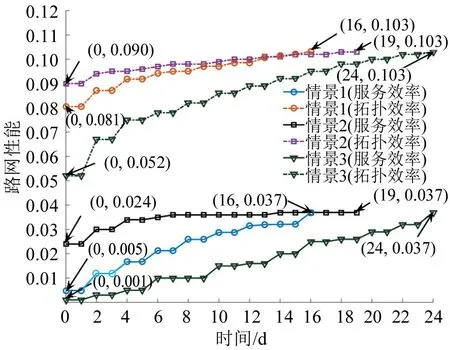
图4 不同情景不同指标下的路网性能恢复曲线Fig.4 Network performance recovery curves under different scenarios with different indicators
图5 为资源条件对路网性能恢复的影响。可以看出,通过增加资源投入,同时维修多个失效节点,可缩短恢复时间,提升恢复速度,减少路网性能损失。以发生扰动情景1为例,如果同时仅能维修1 个节点,路网恢复需要16 d,2 d 后路网服务效率仅为0.012;如果同时维修5 个节点,路网恢复仅需4 d,2 d后路网服务效率可达0.029。
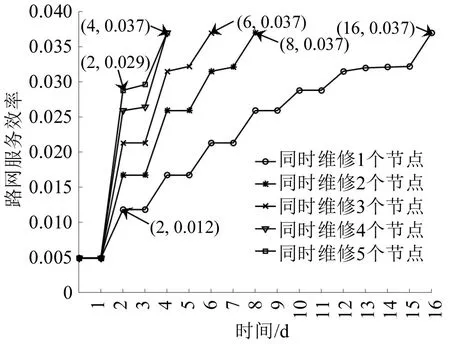
图5 资源条件对路网性能恢复的影响(情景1)Fig.5Impacts of resource conditions on network performance recovery(scenario 1)
表2为路网节点服务效率重要度排序结果,反映单个节点失效对路网服务效率的影响程度。结合图2和表2可以看出,排序前30位的节点均为换乘站。总体来看,度越高的节点排序越靠前,度相同的节点其衔接的线路流量越高重要度排序越靠前。例如:重要度排序第1 的节点32 是1、6、18 号线的换乘站,节点度为6;重要度排序第2的节点12是1、7、18 号线的换乘站,节点度为5;节点18 和节点146 度均为4,但节点18 衔接的1、2 号线比节点146 衔接的5、6 号线具有更高的流量,因此节点18的重要度排序更靠前。
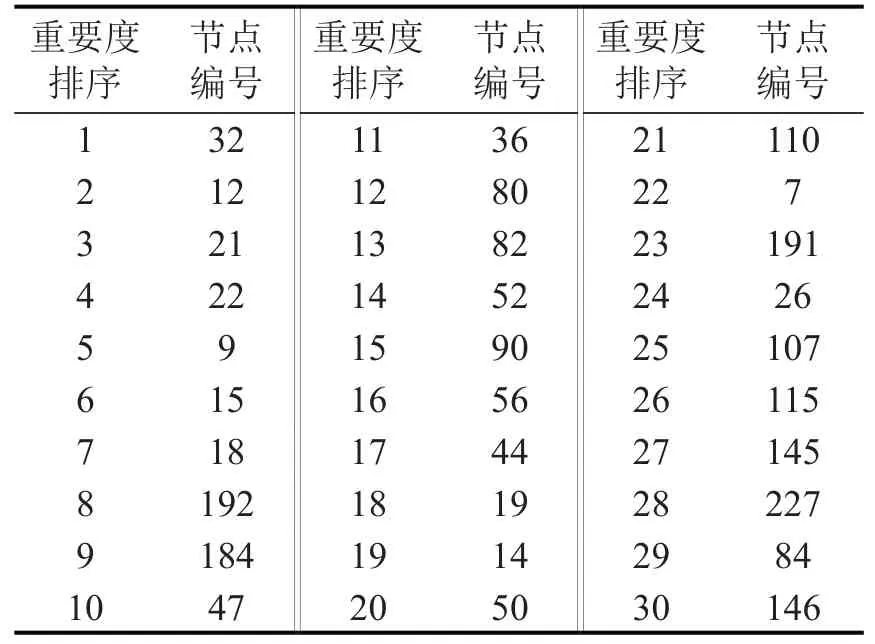
表2 节点服务效率重要度排序Table 2 Ranking results of node importance for service efficiency
表3 为不同恢复策略对路网服务韧性的影响。其中,随机恢复是指随机产生失效节点恢复次序,基于度的优先恢复是指先恢复度高的失效节点,然后恢复其邻近的度较小的失效节点,基于重要度的优先恢复是指按照失效节点的重要度排序确定恢复次序,最优恢复即本文提出的通过优化模型得到失效节点恢复次序。可以看出,3种情景下,最优恢复优于其他3种恢复策略,获得的路网服务韧性最大。例如,发生扰动情景3 时,最优恢复比基于重要度的优先恢复、基于节点度的优先恢复和随机恢复获得的路网服务韧性分别高16.76%、72.11%和86.21%。这一结果表明,对于失效节点较多的情景,如果采用基于重要度的优先恢复、基于节点度的优先恢复和随机恢复,仅能得到次优恢复方案。
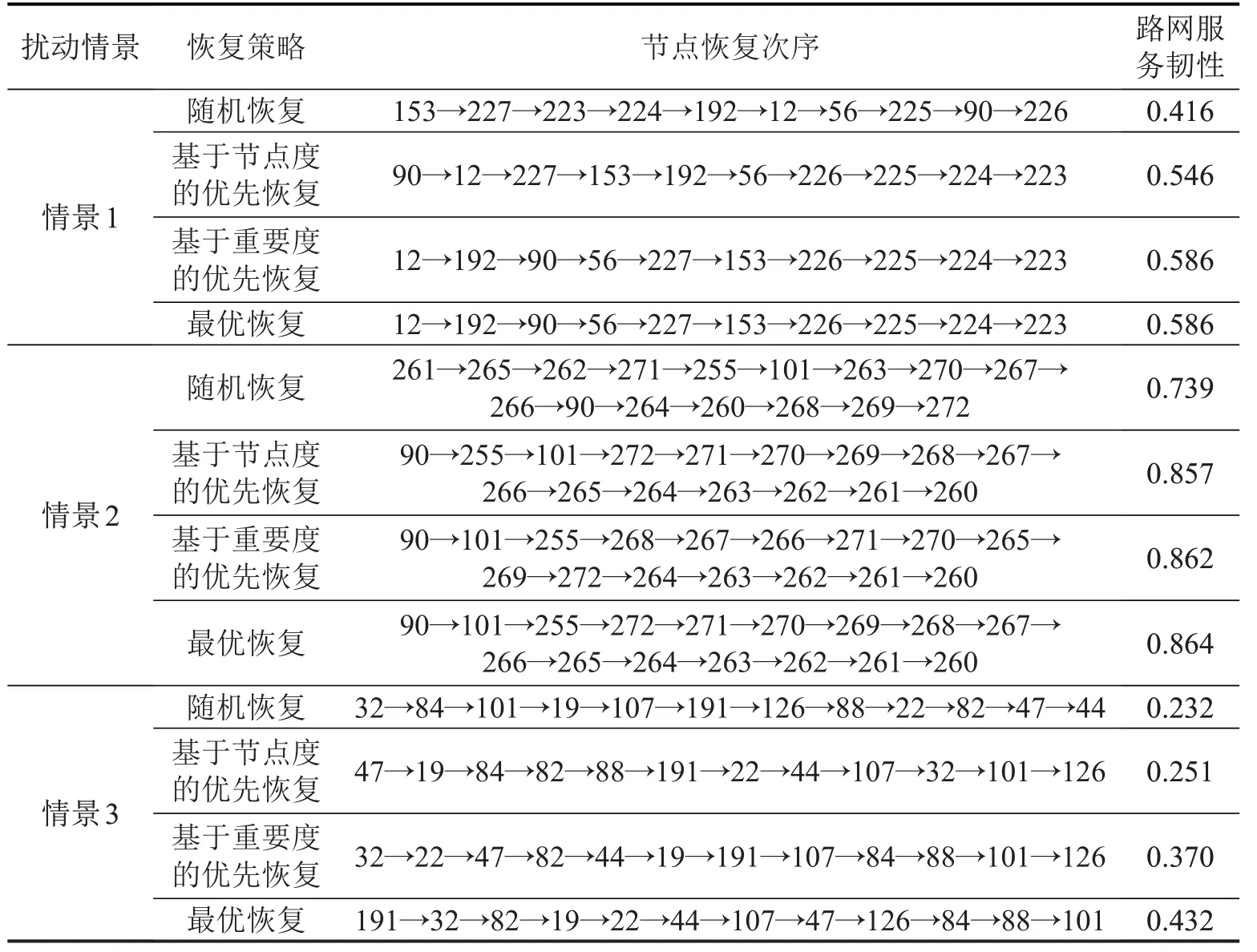
表3 恢复策略对路网服务韧性的影响Table 3 Network service resilience under different recovery schemes
现实环境中,扰动事件导致部分节点失效进而造成部分线路停止运营,原本选择停止运营线路出行的旅客可能仅有部分放弃出行或选择其他交通方式出行,其余将转移至路网中正常运营线路出行。表4 为扰动事件后客流分布变化对节点恢复次序的影响。其中,客流损失系数是指放弃出行或选择其他交通方式出行旅客所占比例。不失一般性与合理性,假定未损失的客流(转移至地铁正常运营线路的客流)成比例分配至正常运营线路中,即线路客流量越大,分担的转移客流越多;同时,假定线路失效节点完全恢复后该线路客流即恢复正常。从表4可以看出,客流损失程度对失效节点恢复次序产生一定影响。例如,若扰动情景1 发生,客流损失系数为0.1 时,节点226 的恢复次序排在1 位;当客流损失系数为0.3 时,节点226的恢复次序排在7 位。这表明在确定失效节点恢复次序时,有必要考虑部分线路停止运营后客流的潜在损失程度。
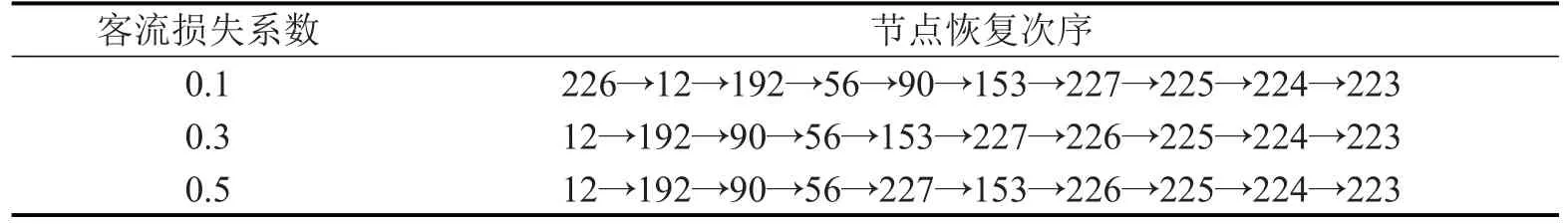
表4 扰动事件后客流分布变化对节点恢复次序的影响(情景1)Table 4 Effects of passenger flow distribution changes on node recovery order after disruption(scenario 1)
4 结论
从地铁运营实际出发,以服务效率为路网性能指标,构建基于服务效率的路网韧性评估模型,提出以路网韧性最大化为目标、基于遗传算法的最优恢复策略。研究结果表明:
(1)基于最优恢复策略,分别以服务效率和拓扑效率作为路网性能指标,获得的失效节点恢复次序明显不同,表明需根据地铁实际运营特点,合理选择路网性能指标,否则可能得到次优恢复策略,无法实现预期恢复目标。
(2)3种扰动情景下,最优恢复策略优于基于重要度的优先恢复策略、基于节点度的优先恢复策略和随机恢复策略,获得的路网服务韧性最大。如果采用除最优恢复策略之外的3种策略,仅能得到次优恢复方案,造成路网服务韧性的潜在损失。
(3)扰动事件导致部分线路停止运营后会造成部分客流的潜在损失,客流的潜在损失程度对失效节点的恢复次序会产生一定影响。
后续将考虑扰动事件对出行决策行为的影响,构建考虑决策行为影响的地铁网络服务韧性评估模型。
