金属材料织构的激光超声检测研究

2021-10-30魏伟

世界有色金属 2021年9期

魏伟

（兰州城市学院，甘肃兰州 730070）

化工设备中的压力容器、泵、管道等都是由金属材料制成，金属材料为多晶材料，晶粒较细。多晶材料的宏观力学性能与其化学成分，尺寸，取向分布，取向关系和晶界结构有关。在铸造、塑件、热处理等金属加工过程中，晶粒在尺寸、取向分布和形状上都会发生变化，从而产生不同的组织。

由于挤压板材料的织构特征，使其在轴向和横向力学性能方面存在着很大的差异，即所谓的挤压效应。大变形冷轧板在不同方向的力学性能、深冲性能和磁能都有很大的差别，当材料的晶体取向分布发生变化时，其性能也会发生变化。近几年来，由于金属材料的微观结构对材料性能的重要影响，国际上大力发展了织构测试技术。对薄板性能进行在线无损检测，是研究组织结构与性能之间关系的重要背景。由于工业生产的需要，人们致力于开发一种有效的测量和计算方法，使金属板材的性能通过测量信息直接得到。但是目前的检测方法存在一定的缺陷，为此，设计了一种基于激光超声的金属材料纹理检测方法。实验结果表明，所研究的检测方法有效解决了传统检测方法存在的不足，具备一定的实际应用意义。

1 基于激光超声的金属材料织构检测方法

1.1 信号处理

信号采集也称为信号提取，一般来说，获得完整的信息必须满足一定的条件[1]。当采样频率超过信号最高频率的两倍时，通过将模拟信号转换为数字信号，采样数据可以描述信号而不会失真，否则将发生频率折叠和频率重复。因此，当信号的最大频率小于尼奎斯特频率时，采样定理可以用采样数据不失真的方式来描述。但在一般的实际应用中，为了保证采样的顺利进行，通常采样频率是信号最高频率的5-10倍。在数据采集后需要对数据进行处理，滤波技术是信号处理中最基本也是最重要的手段，过滤信号可以从复杂信号中提取需要的超声信号，对不需要的部分进行抑制[2]。其计算表达式如下所示：

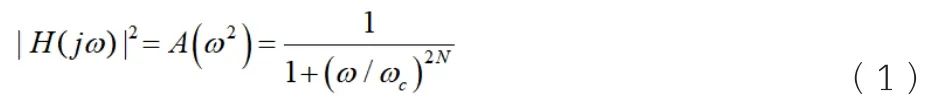
公式（1）中，ωC代表低通滤波器的截止频率，N为滤波器的阶数。

1.2 脉冲激光激发超声解析模型构建

在弹性介质中，金属材料表面受到脉冲激光射入，所出现的位移场即是激发超声的声场。试验中发现，脉冲激光仪所具备脉冲光斑直径和宽度[3]，这两个参数所存在的差异会影响试验结果。因波速直径对于金属材料的横向尺寸而言，激发超声波传播耗时要大于脉冲激光超声用时，因此我们采用点源模型描述脉冲波传播时间问题。假设一个阶跃函数H(t)来作为激光脉冲时间剖面，物质吸收部分激光能量引起的瞬态温升将使体积V增大产生体积膨胀。

公式（2）中，α代表线形膨胀系数，Cp表示比热，ρ代表样品密度，Q表示吸能转化为电磁能量。

1.3 检测数值模拟

现有的数值模拟方法主要有两种：差分法和积分法。差分法主要建立基本方程，并设定相应的定解条件，得到了近似解，该方法常用于解决空间坐标系下的流场问题。金属材料组织结构检测遇疑难问题时可以应用有限差分法进行求解，但这种方法也存在一定弊端，计算结果可能存在一定的误差。积分法是在建立基本方程基础上进行求解，此方法不能构造出近似函数，有一定规律的几何结构问题可以应用积分法进行解决。在数值计算与分析方面，有限元法也有很大的贡献，其可将连续解域离散为多个小单元，然后以某种方式合并为一组单元，全解域解中的未知场函数是由各单元内的假定近似函数表示的，无限连续自由度问题的特点是有限离散自由度。为此经过上述分析采用有限元方法，对激光激励超声在材料表面的作用进行了模拟计算[4]。

1.3.1 激光超声的有限元形式

采用有限元法进行热分析时，其瞬态过程热传导方程可表示为：

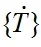
1.3.2 激光作用的力函数

在此基础上，设计激光作用的力函数。采用高斯分布函数，建立了脉冲激光作用下的等效功率函数，激光与物质相互作用时，热传导在能量交换中占主导地位。这一计算并未考虑物质本身对外界的热辐射和热对流，将激光器吸收的能量转化为热能，用激光函数的空间分布来表示高斯函数的分布，用材料吸收的能量来表示：

公式（5）中，I0是脉冲激光的功率密度，A(T)代表物料表面吸附能力，f(x,y)、g(t)脉冲激光的时空分布函数的单独表征。

1.3.3 时间步长与单元长度的选取

将材料离散成若干不重叠的单元是FEM的主要方法，建立有限元模型时，数值积分的稳定性容易受到时间步长和单元长度的影响。随时间步长减小，解的精度提高，超声高频成分识别量增加，用最少的时间步长可以得到高精度的解[5]。采用二维傅里叶变换法分析时域波形时，时间步长的选择也将影响傅里叶变换的精度，同时，也避免了重叠的发生。但是，如果时间步长过小，就会使有限元计算的计算量大大增加。构建有限元模型求解时，首先要保证较高的求解精度，尽可能选择合适的时间步长，而时间步长可以是：