直流配网用级联DC−DC变换系统稳定性分析

杨国朝，杨朝雯，刘仲英，张宏艳，杨智

（国网天津市电力公司城东供电分公司，天津 300250）

随着分布式能源技术的不断发展，如光伏、风能等越来越多的新能源以及锂电池和超级电容等储能环节被应用在电网系统中，可以预见，未来电网配用电系统中源−储−荷多为直流的用电形式。同时由于电力电子技术的不断突破，使得电力电子设备的成本与体积不再成为构建直流电网系统的限制。因此，随着电力电子技术的发展，直流配用电技术经济优势逐渐显著，采用直流配用电系统可有效减少传统交流系统中不可避免的整流和逆变等功率变换环节，从而避免了其中产生的损耗，提高了共用电系统的能效。因此，直流电网系统相关领域具有广泛的研究空间和发展应用潜力，受到了世界各国学者的重视[1−3]。

目前，直流微电网典型结构如图1所示。从图中可以看出，风电、光伏以及新能源汽车等系统源和储能单元产生的功率流通过前级直流变换器首先汇集到直流母线统一电压，再通过DC−DC将电能传输给直流用电负荷。而这种双级DC−DC变换器的级联型结构可能会引起系统内部输出电压不稳定现象，影响系统可靠工作运行。

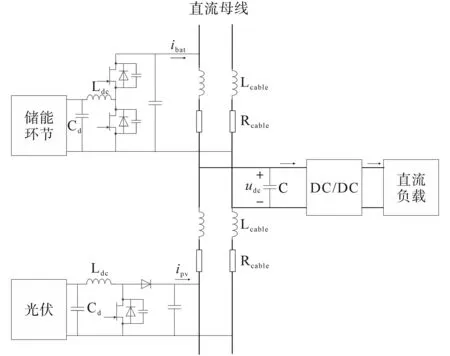
图1 直流微电网典型结构Fig.1 DC microgrid typical structure

文献[4−5]阐述了可用于判定级联直流变换器结构稳定性的主要判据，即Middlebrook判据，从而通过该方法可以判定级联系统的稳定性，保证系统可靠运行。在此基础之上，利用该判据也可以进一步优化级联型谐振变换器的参数优化设计并保证系统的动态性能。而LLC谐振变换器凭借其软开关特性，具有高增益、高效、高功率密度的应用潜力以及电气隔离的安全保障等优势越来越受到学者的广泛关注。其应用范围也在逐步扩大，近些年已经被应用于直流微网系统之中。因此，作为级联DC−DC的前级变换器可以很好地发挥其优势，具有很好的应用潜力[6−7]。

为了适应更多的应用负载电压等级，采用Buck变换器作为级联变换器的后级进行具体的调压应用。而对于较为成熟的Buck变换器，其稳定性的研究自然受到学者的重视。文献[8−9]针对Buck变换器进行了细化研究，建立了对应模型，详细分析了对变换器稳态输出有影响的干扰因素及其作用。文献［5］详细介绍了计算Buck变换器和半桥变换器的输入、输出阻抗的方式。

本文仅以单输入单输出的级联DC−DC功率变换系统为研究对象，以LLC为前级变换器，Buck拓扑为后级变换器为例展开分析。其中，后级Buck变换器通过变占空比调压来实现用电负荷的多电压等级用电需求，而前级LLC拓扑则用高压直流侧的高增益变换为Buck提供低压母线电压，采用在谐振频率点附近工作，避免波形畸变带来的无功损耗，从而使系统获得较高的工作效率。以LLC+Buck为例进行说明，介绍了含有隔离型谐振拓扑的级联DC−DC变换器的建模方法、稳定性分析方法及参数设计优化方法。采用Pisim和Matlab等电力电子仿真软件进行验证，最终通过样机验证理论分析及参数设计方法的有效性，可有效提高直流配用电系统的稳定性。

1 LLC+Buck级联拓扑

作为直流配用电系统的关键核心设备DC−DC变换器需要具有高效、稳定等特征，同时还应尽可能地提高设备的功率密度，满足用户小型化的需求节省空间成本。因此，本文选用LLC-Buck级联型拓扑作为研究目标，如图2所示。一方面前级LLC具有电气隔离的特性保证使用安全，同时可实现变换器高增益和高效率功率变换；另一方面，后级Buck可通过灵活地占空比调节实现低电平宽范围电压调节。

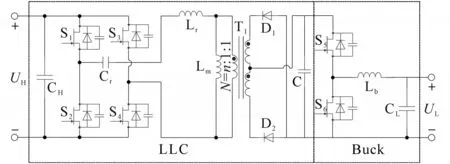
图2 LLC-Buck级联型拓扑仿真结构Fig.2 LLC-Buck cascaded topology simulation structure

图2中LLC结构由高压逆变全桥S1～S4、推挽结构D1～D2、谐振电感Lr、谐振电容Cr以及变压器T1构成；Buck结构由开关管 S5～S6、储能电感 Lb以及低压滤波电容CL构成；CH，C分别为高压稳压电容和LLC输出稳压电容；Lm为变压器T1的励磁电感；UH，UL分别为输入高压和输出低压。

2 Buck电路输入阻抗分析

Buck电路作为后级用于精确输出调压的变换器，根据Middlebrook判据描述，其输入阻抗对于整个系统的稳定性判定具有重要意义。因此，给出典型Buck电路等效小信号模型如图3所示。

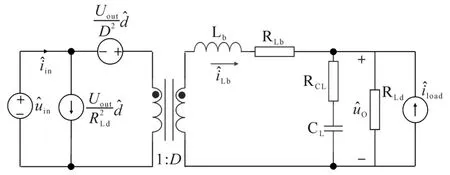
图3 Buck电路小信号模型Fig.3 Small signal model of Buck circuit

从图3中可以看出，系统所涉及的扰动包括Buck输入电压扰动 ûin、占空比扰动 d̂以及负载电流扰动îload。根据叠加定理，可以获得对应的等效结构如图4所示。

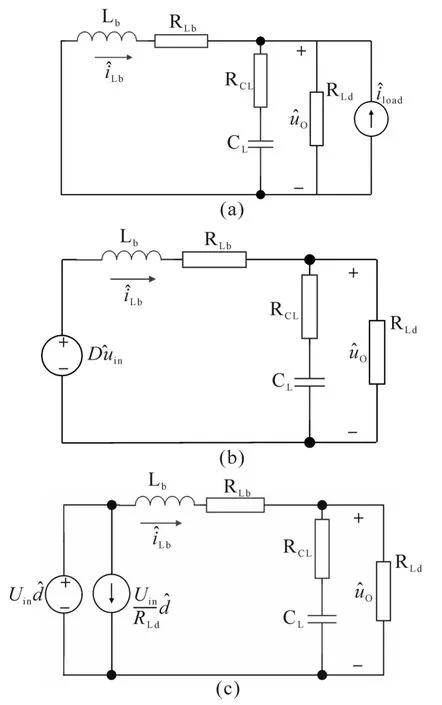
图4 Buck电路小信号模型等效结构Fig.4 Small signal model equivalent structure of Buck circuit

图 4a中，将d̂和 ûin置 0获得变换器开环工作电路，不难得到对应的输出阻抗为

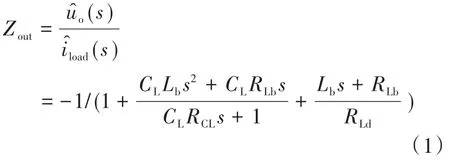
图 4b将d̂和 îload置 0 获得中给出结构，可以得到 ûin与 ûo的增益关系 Gvg；对应的图 4c中将 ûin和îload置 0，可以获得 d̂与 ûo的对应关系 Gvd，分别如下式所示，其中Z为中间变量。

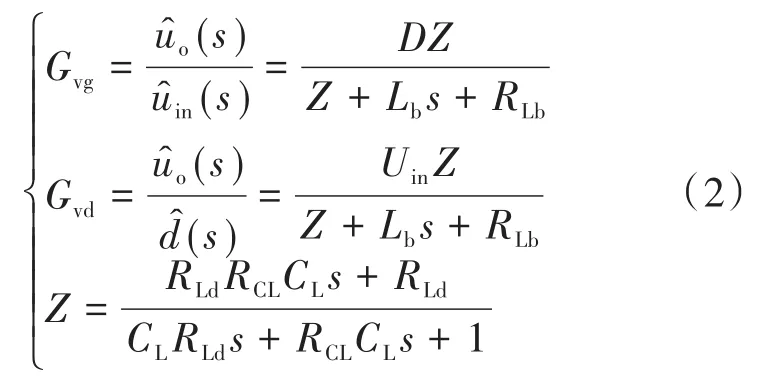
最终，可以获得ûo与各扰动的关系如下：

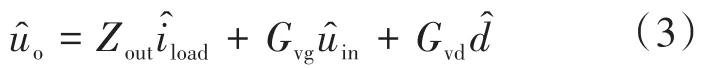
同理，可得电感电流îLb与各扰动的关系如下：

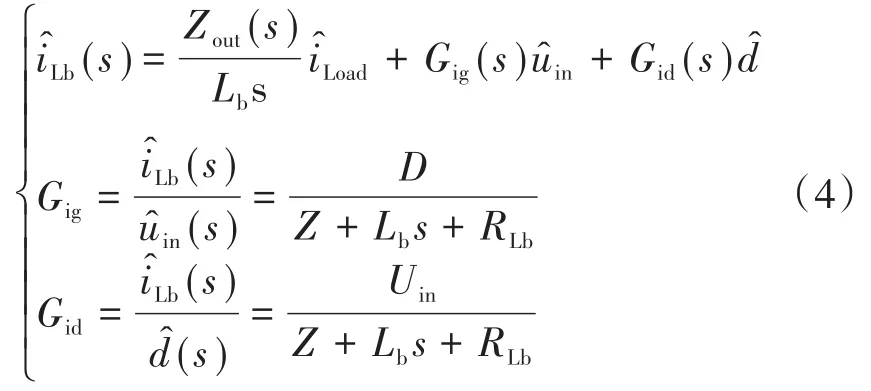
最终获得开环输入阻抗为

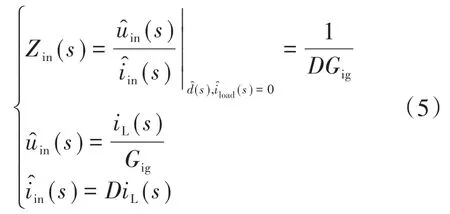
Buck电路电压闭环控制框图如图5所示。根据上述所得各信号传递函数，并结合图5可以获得闭环输出和输入阻抗，如下式：

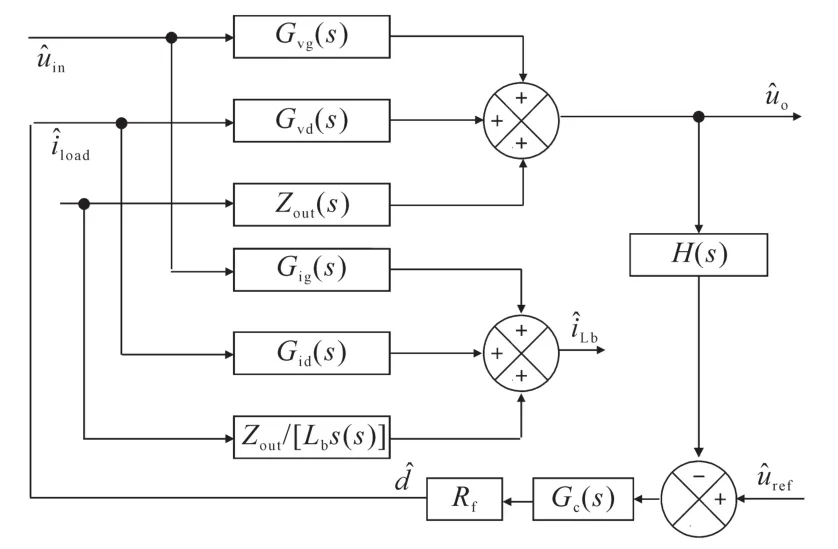
图5 Buck电路电压闭环控制模型图Fig.5 Model diagram of Buck circuit voltage closed-loop control

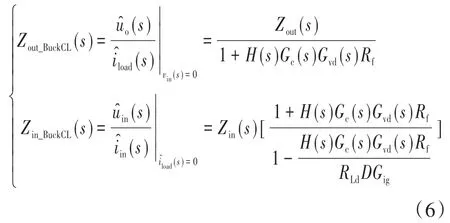
式中：H（s）为对应反馈传函；Gc（s），Rf为对应增益。

3 LLC输出阻抗分析

为了更好地分析级联系统的整体稳定性，采用相同的方法，需要对LLC拓扑进行分析，建立对应的等效小信号模型[10−13]，并计算其输入阻抗。由于LLC拓扑较之与Buck结构较为复杂，得到其稳态等效电路如图6所示。

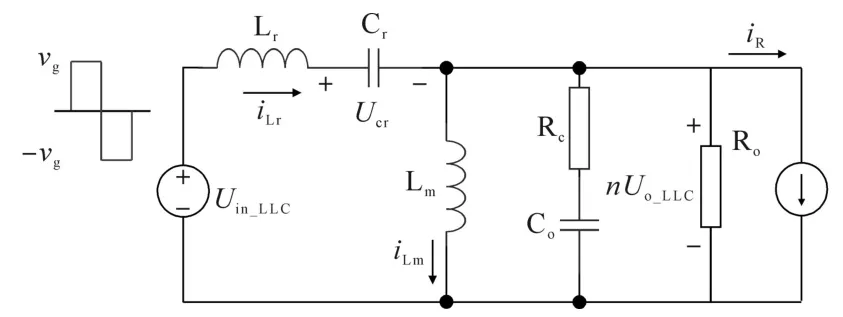
图6 LLC基波等效稳态模型Fig.6 LLC fundamental wave equivalent steady state model

图6中，Uin_LLC为等效基波输入电压，其波形如vg所示。iLr为谐振腔电流，iLm为变压器励磁电流，Uo_LLC为交流等效输出电压，Ucr为谐振电容电压，Rc为滤波电容等效串联电阻，Ro为等效基波负载。根据基波等效分析理论，非线性变量可以近似等效为直流分量或基波分量。当LLC谐振变换器稳态运行时，由基波等效分析方法和基尔霍夫电压电流定律可以近似推出LLC大信号模型的状态方程为

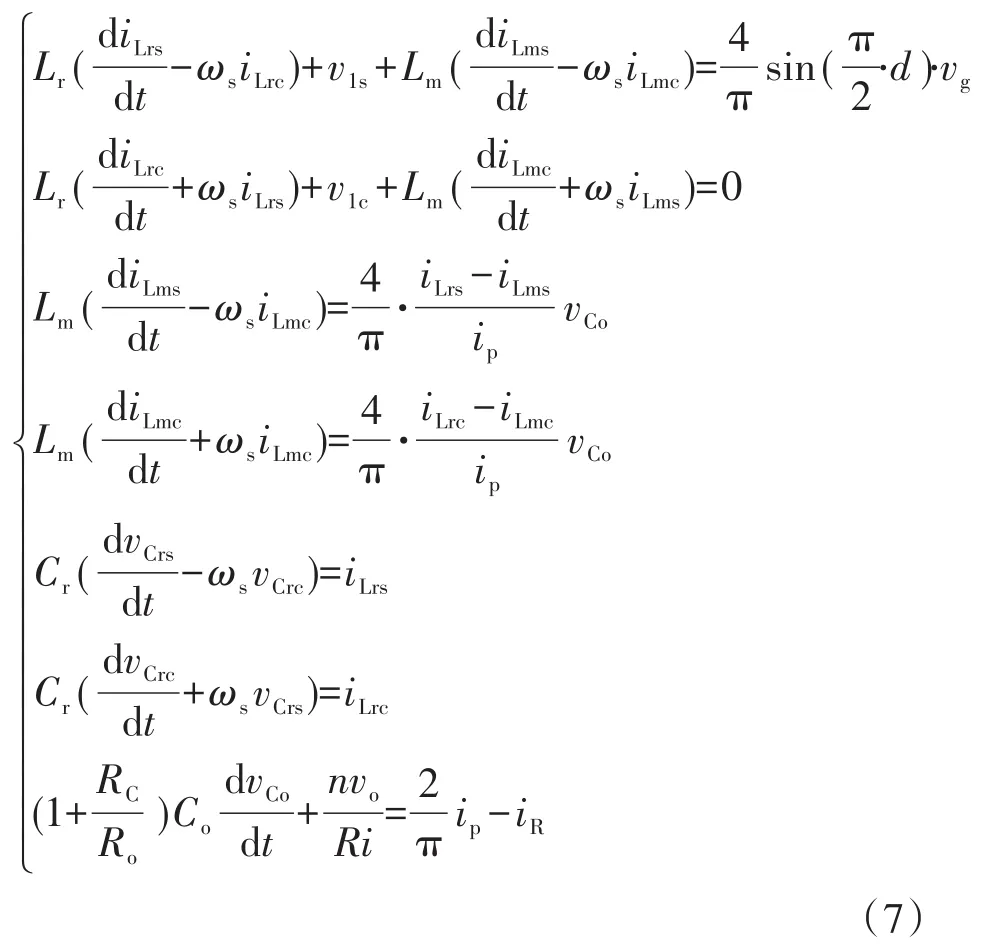
式中：iLrc，iLrs，iLms，iLmc分别为谐振电感电流与励磁电流的正弦分量与余弦分量；vCrs，vCrc为谐振电容电压的正弦分量与余弦分量；vCo为输出电容电压。对应的输出方程式如下：

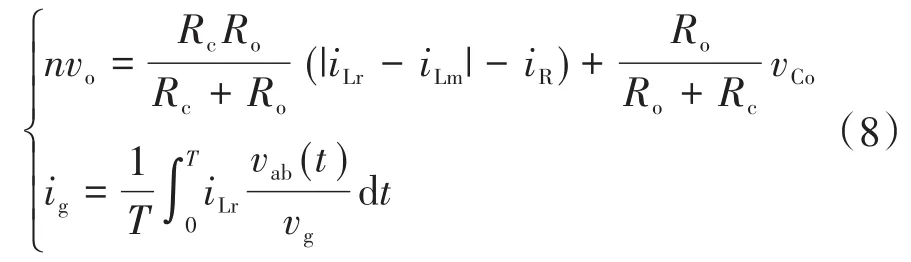
结合LLC的大信号数学模型和输出方程得到对应的稳态解。同时，加入对应的扰动量，即可获得LLC的等效小信号模型，如图7所示。

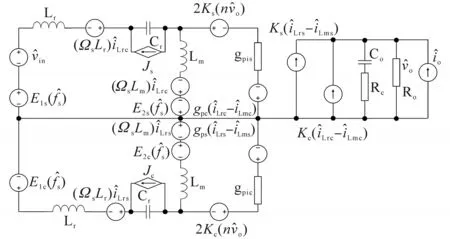
图7 LLC小信号等效模型Fig.7 LLC small signal equivalent model

闭环控制框图如图8所示。按照分析Buck电路相同的方法得到对应信号的传递函数。根据所得传递函数。图8得到LLC的电压闭环输出阻抗如下：

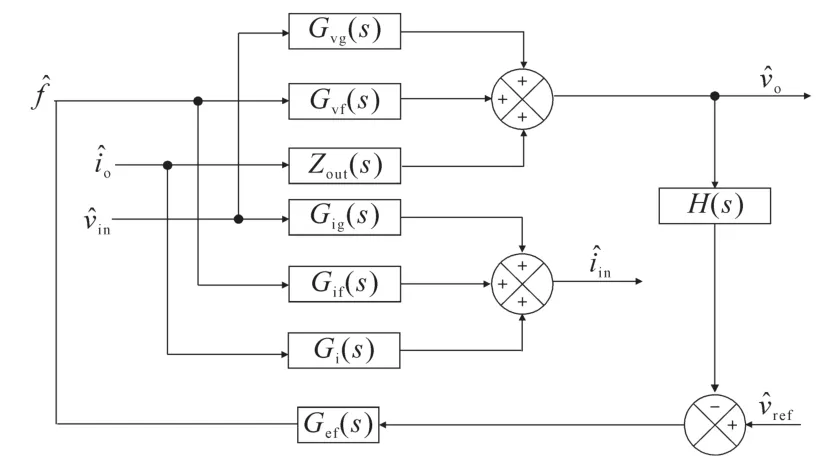
图8 LLC闭环电压控制框图Fig.8 LLC closed loop voltage control block diagram

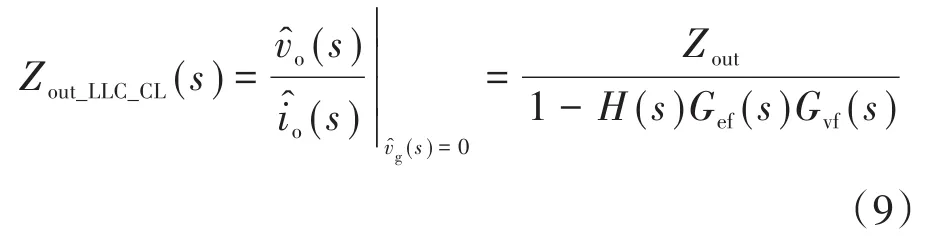
式中：Gef（s），Gvf（s）为对应的参数增益传递函数。

4 级联系统稳定性与参数设计

在满足前级LLC谐振变换器和后级Buck都能各自稳定的情况下，级联系统也仍然会出现不稳定的现象[5]。根据前文所提及的Middlebrook判据，在本系统中即可表示为

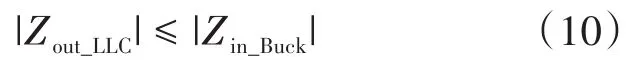
因此，基于该稳定判别标准同时结合前文分析所得的Buck输入阻抗和LLC输出阻抗，如式（6）、式（10），可以获得新的参数设计限制条件以保证系统的整体稳定性，并建立对应的参数设计方法如图9所示。参数设计流程如下：

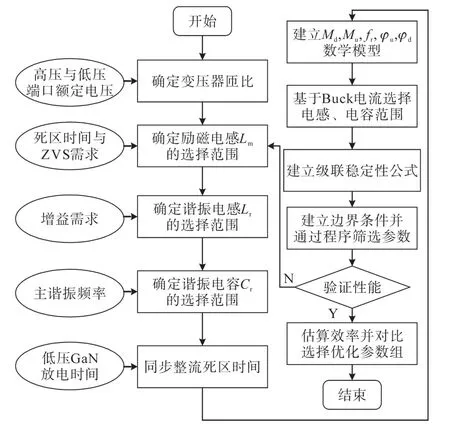
图9 参数设计流程图Fig.9 Program of parameter design

1）根据需求输入输出电压，确定变压器的匝比；

2）基于额定工作状况下实现ZVS所需时间最短时间以及死区时间需求确定Lm的取值范围；

3）根据变换器应用的增益需求和工作频率确定Lr和Cr的选值变化范围；

4）基于GaN特性获得同步整流死区时间；

5）基波等效分析法建立谐振变换器稳态分析模型；

6）基于功率级和电压确定后级电路中的对应参数的取值范围；

7）推导出前级谐振拓扑的输出阻抗和后级拓扑的输入阻抗，并基于Middlebrook判据，建立稳定性限制条件。

8）根据所得数学模型以及应用需求建立对应的M，fr，输出、输入电压，φ，ZVS实现以及稳定性等限制条件，在Matlab中建立程序进行轮寻筛选，寻找符合应用需求的参数组；

9）记录所有符合条件的参数组，并验证参数特性是否真正满足需求；

10）基于所得参数组，以效率为优化目标，分别计算获得最优的参数组。

最终获得对应的变换器设计参数如下：Lr=5 μ H，Cr=20 nF，Lm=100 μH ，n=7.8∶1∶1，vin=375 V，Co=200 μF，Rc=0.15 mΩ，Lb=1.2 μH，RLb=1 mΩ，CL=100 μF，RCL=0.3 mΩ，fLLC=500 kHz，fBuck=400 kHz。

5 仿真与实验

基于参数设计所得的对应参数搭建级联型变换器电力电子仿真模型，并进行仿真与实验验证。两级DC−DC输出输入阻抗对比图如图10所示。

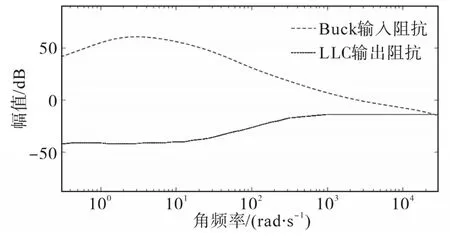
图10 两级DC−DC输出输入阻抗对比图Fig.10 Comparation of open-loop output and input impendence of cascaded DC−DC

从图10的级联DC−DC输出输入阻抗对比图中可以看出，在通过加入稳定性限制条件后所得的变换器参数具有良好的稳定运行效果。

对应的实验波形如图11所示，图11a中VLLC，VBuck分别为LLC和Buck拓扑的输出电压，可以看到其输出稳定性。图11b为LLC拓扑中高压开关管的ZVS软开关示意图，虚线圈内部分可以明显看出软开关的实现。iLr为Lr的谐振电流，VS1_GS为开关管S1的驱动电压，VS1_DS，VS2_DS则分别为S1和S2开关管的源漏极电压。

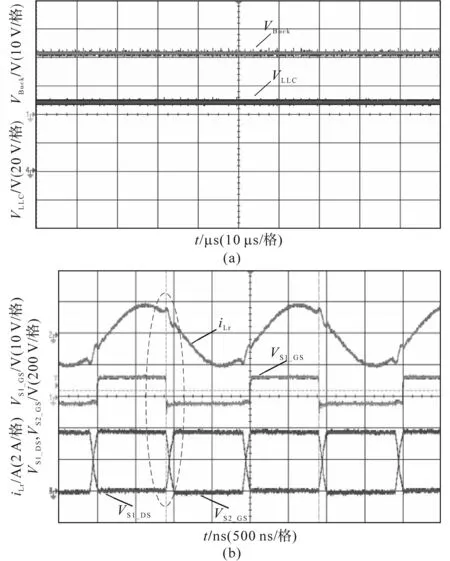
图11 两级DC−DC实验波形Fig.11 Cascade DC−DC experimental waveforms

从实验中可以看出变换器具有良好的软开关特性及输出电压稳定性。保证了变换器的高效稳定运行，同时验证了前文理论分析的准确性和正确性。

6 结论

本文主要针对直流配用电系统中所涉及的双级DC−DC变换系统稳定性进行分析。以LLCBuck的拓扑结构为例，基于Middlebrook判据进行具体的建模分析，详细地给出了Buck以及LLC的小信号建模过程，得到对应的输入输出阻抗。在此基础之上，提出了优化的参数设计方法，并结合Matlab仿真软件与实验验证了系统的稳定性与理论的正确性。