电控伺服助力器测试ADRC高速加载研究

范习谦，范伟军，孙正

（1.哈尔滨理工大学机械动力工程学院，黑龙江 哈尔滨 150080；2.中国计量大学计量测试工程学院，浙江 杭州 310018）

电控伺服助力器在进行综合性能检测时，要求输入端加载电动缸快速达到指定速度，模拟车辆快速制动时高速踩踏的工况。依据国内某厂家的技术要求，电控伺服助力器输入端的最大加载速度需达到200 mm/s，被测样件加载全行程约为43 mm。在实际试验测试过程中，加载端电缸加速过程受限于电缸自身加速度数值与较小的位移行程限制，虽可设定较大的电缸目标加载速度，往往电缸已经走完加载行程而加载速度尚未达到设定的目标值，无法满足高速加载检测需求。

在传统的工业自动化控制中常用比例积分微分控制算法（PID）来实现固定行程的速度控制，PID控制算法以结构简单、可靠性强、工作稳定等特点在工业自动化行业中占据主导地位，其主要控制原理是基于对误差的比例、积分、微分的综合调控来实现控制。PID控制算法简易可靠、鲁棒性强，但是它存在误差取法不严谨、误差相对于时间的微分取法待商榷、加权和策略未最佳、积分反馈存在副作用等问题，会在一定程度上对测试系统控制带来负面影响[1]。

为克服上述PID控制算法中的四个缺陷，系统电动缸速度控制部分引入自抗扰控制（active disturbance rejection control，ADRC）算法，分别安排过渡过程对应设置跟踪微分器合理获取误差相对于时间的微分、使用非线性组合在非线性区域获取更好的加权和策略组合、设置扩张状态观测器抑制积分反馈副作用等解决方案，同时沿用PID控制算法中的控制原理，保证ADRC自抗扰控制算法的可靠性与鲁棒性。

1 高速加载ADRC算法建模

自抗扰控制结构框图如图1所示，v为系统输入信号，v1为v的过渡信号，v2为输入信号v的微分信号，u0为矫正信号，u为系统控制信号，z1为状态量观测信号，z2为观测信号微分信号，z3为系统总扰动估计信号，b0为系统模型参数，y为系统输出信号。

图1 自抗扰控制结构框图Fig.1 Structure diagram of ADRC system

ADRC的核心有三大模块：跟踪微分器、扩张状态观测器和非线性状态误差反馈。微分跟踪器主要可以安排过渡过程，接收到期望控制信号后，控制系统可以通过微分跟踪器调整控制，获得控制系统加速度先增后减、速度单调上升、无超调量的过渡过程，加快响应速度[2]。扩张状态观测器主要是进行扰动的观测，对系统未知建模部分和外部扰动的总和控制量进行实时评估并用于补偿，能够有效处理控制系统中的各种不稳定因素。非线性状态误差反馈主要在加入扰动补偿时通过调节补偿项来提升控制系统的效率，增强系统鲁棒性。模型中两个非线性函数fhan(x,α,d)和fhan(x1,x2,r,h)的定义分别如下两式所示：

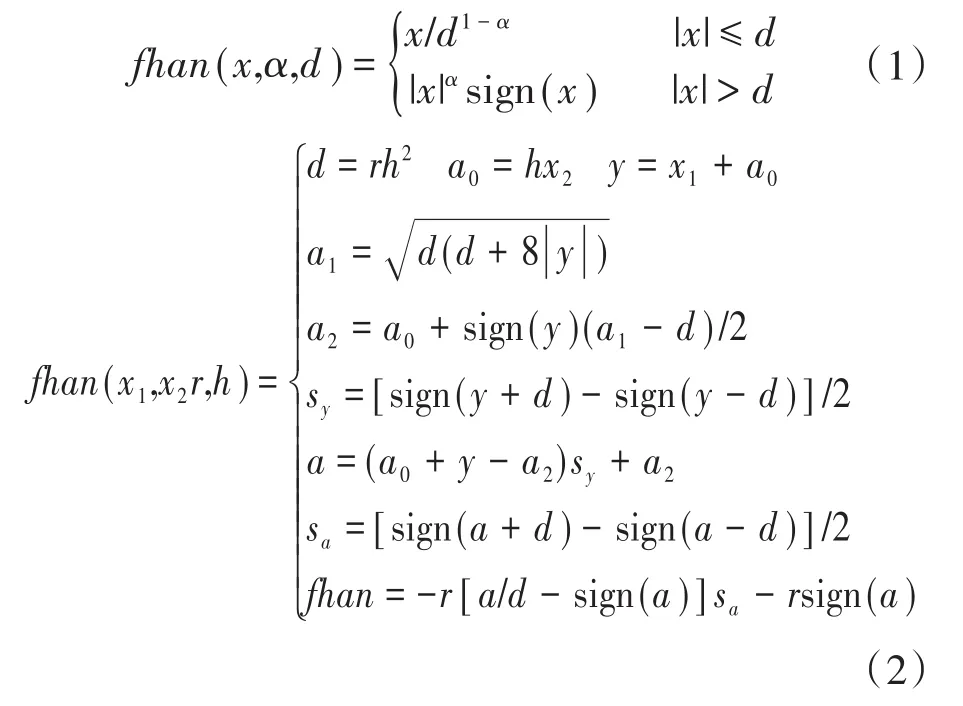
为了获得最佳自抗扰控制策略，需完成跟踪微分器、扩张状态观测器和非线性状态误差反馈的数学建模及参数整定，各模块参数整定基于“分离性原则”独立进行。

1.1 跟踪微分器建模及参数整定

跟踪微分器的设计目的在于实现系统输入信号v的实时跟随，安排相对稳定且适宜的过渡过程，减少噪声干扰信号，从而顺利获得微分de/dt，同时降低速度超调，减少电动缸加速时间。跟踪微分器数学模型可以表示为下式：

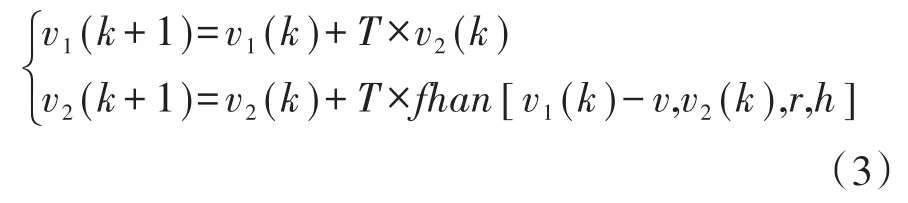
式中：v1为系统输入信号的快速跟踪信号；v2为对v1以积分方式合理提取的微分信息，为v的近似微分信号；T为跟踪微分器的采样周期；r为跟踪速度因子；h为滤波因子。

采样周期T取决于被控伺服电动缸的响应速度，考虑到快速控制，系统采样周期T为0.001 s；参考伺服电动缸以及自抗扰控制算法中的信号干扰大小，可整定获取跟踪速度因子r和滤波因子h。考虑到异常情况下，系统输入信号v中可能混入噪声信号，影响系统控制效果。为减弱噪声信号的负面影响，需要调整滤波因子h，对系统输入信号v进行滤波处理。参数整定过程中，需要控制好滤波因子h的数值大小，滤波因子h必须大于采样周期T，才会有较好的滤波效果，但过大的滤波因子h会造成跟踪信号的失相。经过多组数据的比较，滤波因子h确定为3T。

跟踪速度因子r的大小与控制系统的速度跟踪能力呈正相关关系，即增大跟踪速度因子r能够提升跟踪信号v1的跟踪速度[3−4]。过大的跟踪速度因子r会为控制系统引入一定量的超调量，影响控制效果。此时需要牺牲部分系统跟踪速度以换取系统超调量的减小，实现稳定控制[5]。根据数学模型对多组速度因子数据的仿真分析，系统速度因子r取200时，系统跟踪信号的调节时间和超调量满足控制要求。

综上所述，系统整定跟踪速度因子r和滤波因子h直至获得电动缸加速时间短、速度稳定且超调量小的运动过程，完成跟踪微分器的参数整定后，跟踪速度因子r和滤波因子h在扩张状态观测器和非线性状态误差反馈的参数整定过程中可以持续使用。

1.2 扩张状态观测器建模及参数整定

作为自抗扰控制算法的关键算法部分，扩张状态观测器的主要功能是实时监测系统环境内外部的扰动，并对系统总扰动进行计算与补偿。扩张状态观测器数学模型可以表示为下式：

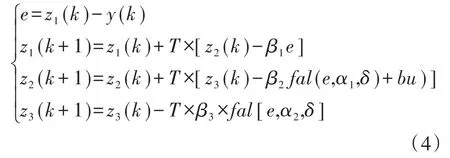
式中：β1，β2，β3为扩张状态观测器的校正增益；fal(e,α1,δ)为非线性函数；α1，α2为非线性因子；e为非线性函数误差；α1，α2为e的指数；b为补偿因子；u为非线性状态误差反馈的输出量；δ为非线性函数误差定义域的区域宽度。

校正增益β1，β2，β3主导控制扩张状态观测器的基本性能，为获得最佳的扰动补偿效果，通过反复调整校正增益 β1，β2，β3，使被控伺服电动缸系统内外的总扰动对系统产生的负面影响被基本消除。

由于扩张状态观测器的扰动补偿效果影响着自抗扰控制算法的实际使用情况，校正增益β1，β2，β3分别影响着状态量观测估计信号z1，观测估计信号微分信号z2，系统总扰动估计信号z3。参数整定过程中，需要适度调整校正增益β1，β2，β3的参数值，避免太大的增益数值过度放大被控信号幅值，保证自抗扰控制系统整体运行效果。非线性函数fal(e,α1,δ)的主要控制因素有三个，分别是非线性函数误差e，非线性因子α1，α2以及非线性区间宽度δ。其中非线性函数误差为过渡信号与状态量观测信号的差值。非线性因子α1，α2控制着非线性函数的曲线图样，在扩张状态观测器的参数整定中，选取适当的非线性因子使得α1>α2[5]。

本系统α1取值0.5，α2取值0.25，δ取值0.001。系统采用单纯型号法，基于最好点位极小值点寻优整定扩张状态观测器的校正增益[6]，β1，β2，β3的值分别为160，1 200，14 000。

1.3 非线性状态误差反馈建模及参数整定

为了提升自抗扰控制算法的稳定性能，系统引入了非线性状态误差反馈，扩张状态观测器通过获取系统总扰动，并控制调整扰动补偿，实现增强自抗扰系统稳定性与鲁棒性的目的[7]。非线性状态误差反馈数学模型可以表示为下式：

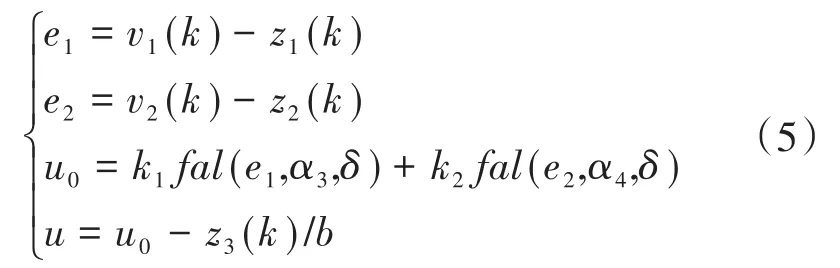
式中：k1，k2为非线性状态误差反馈的增益系数；α3，α4为非线性因子。

非线性状态误差反馈增益系数k1和k2能够以一定数值比例来控制过渡信号与输入信号微分信号、反馈系统输入信号的变化速率，参数整定过程中需要多次调整增益系数k1和k2的数值，以达到较好的控制效果。类似于扩张状态观测器中的非线性因子α1，α2和非线性区间宽度δ，非线性状态误差反馈中的非线性因子α3，α4也控制着非线性函数的曲线走势，非线性区间宽度δ也决定着非线性函数的工作区间。依据整定经验[8]，α3，α4分别取值0.75，1.25，δ取值0.001。补偿因子b决定着系统矫正信号的大小，需依据实际参数整定过程进行实时调整。

参数k1，k2的整定参照经典PID调节的经验进行，整定参数时以k2为主，并协同调整k1，参数k1，k2的整定值分别为16，4.6。

2 高速加载ADRC控制仿真

根据上述ADRC自抗扰算法建模以及主要相关参数整定，利用Simulink仿真软件，对跟踪微分器、扩张状态观测器、非线性状态误差反馈进行单独数学建模以及模型封装，如图2、图3、图4所示。

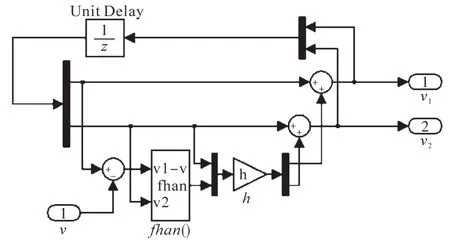
图2 跟踪微分器仿真建模图Fig.2 Simulation modeling diagram of the tracking differentiator

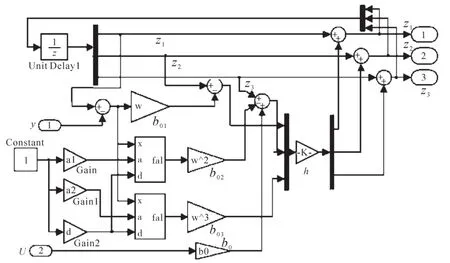
图3 扩张状态观测器仿真建模图Fig.3 Simulation modeling diagram of the extended state observer

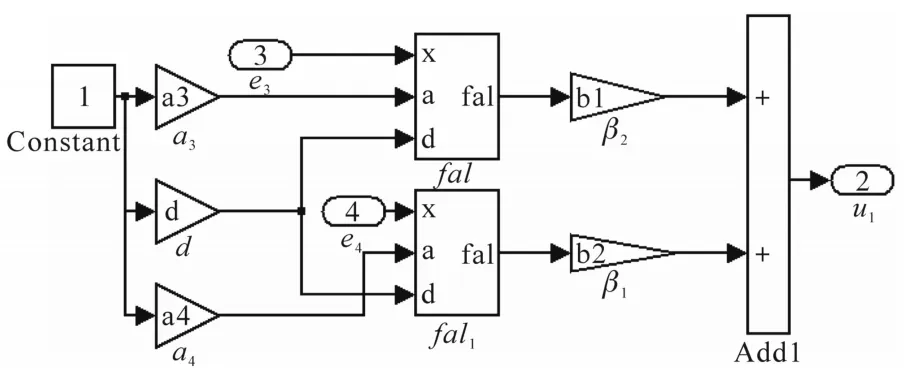
图4 非线性状态误差反馈仿真建模图Fig.4 Simulation modeling diagram of nonlinear state error feedback

通过初始参数的整定与修正，使用仿真建模模型对电动缸加载速度变化进行模拟仿真。查阅相关技术文献资料可得，电动缸控制系统主要由电流环、速度环及位置环组成[9]，其中电缸电流环传递函数G(s)[10]如下式所示：

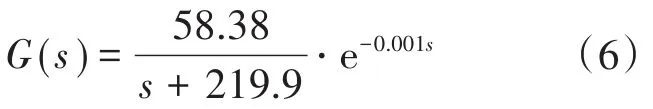
依据控制参数整定结果以及电缸传递函数等环境条件，完成ADRC自抗扰控制下的电缸控制系统仿真，仿真结构框图如图5所示。

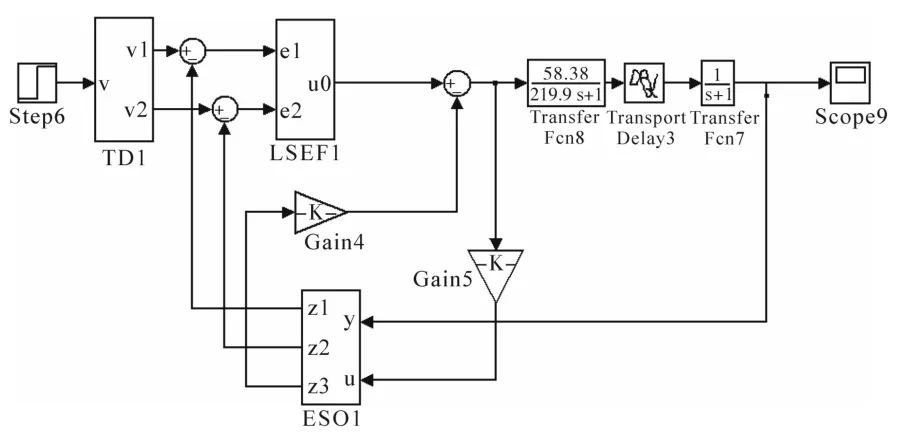
图5 电动缸自抗扰控制仿真建模图Fig.5 Simulation modeling diagram of electric cylinder ADRC

为了更加明显地展示自抗扰控制器的工作性能，利用Simulink软件中现有的PID仿真控制模块对典型PID算法下的电缸速度运动控制数学模型进行建模仿真。在对PID控制算法的控制参数进行调节时，遵循“比例、积分、微分”的先后调控顺序，在PID控制模型的建立过程中采用临界比例度法完成参数整定[11]。

以美国派克汉尼汾公司的高推力电缸ETH080为加载电缸，伺服电机使用派克无刷伺服电机SMH82为例进行加载及仿真分析[12]，该加载系统最大加载速度为200 mm/s，最大加速度为4 m/s2。以电控伺服助力器输入端最大需求加载速度200 mm/s为目标速度值，分别使用上述的在ADRC，PID控制下的电缸运动控制模型进行仿真测试。测试结束后，加入电缸实际运动速度变化曲线与仿真测试曲线进行对比，试验对比结果如图6所示。

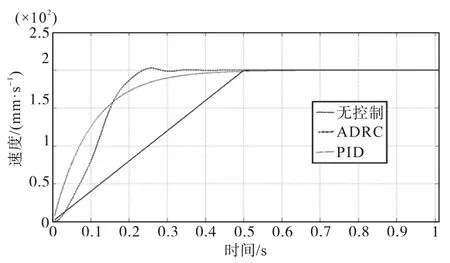
图6 速度设定值仿真响应曲线Fig.6 Simulation response curves of the speed setting value

图6中实线为实测电缸运动曲线，虚线分别为ADRC，PID算法控制下的电缸运动曲线。由仿真响应曲线对比可得，实测的电缸加载运动曲线在稳定加速度的情况下，电缸加速到200 mm/s的速度需要0.5 s的加速时间，PID控制算法下的电缸也需要消耗0.5s的加速时间才能达到200mm/s的电缸速度，而ADRC算法控制下的电缸，在加载前期缓慢增加电缸加速度，电缸加速由慢变快，加载后期电缸加速度缓慢减小，电缸加速由快变慢，到达最大需求加载速度后电缸速度趋于稳定，从电缸开始加速到实现200 mm/s的速度输出，所需加速时间约为0.3 s。相较于没有算法控制下电缸与PID算法控制下的0.5 s，ADRC控制下的电缸加速时间大大缩短，这为较小距离位移下的高速电缸加载提供了解决方案，使电缸运动控制能够满足系统设计需求。

3 试验数据分析

基于上述响应曲线分析，选用ADRC自抗扰控制算法对电缸进行控制，电缸ADRC加载仿真运动曲线与实际运动曲线如图7所示。由曲线对比图可知，电缸实际运行情况下能够按照控制算法运动策略进行加载运动，加速到指定运行速度所需时间与仿真情况下基本一致，能够满足试验测试需求。

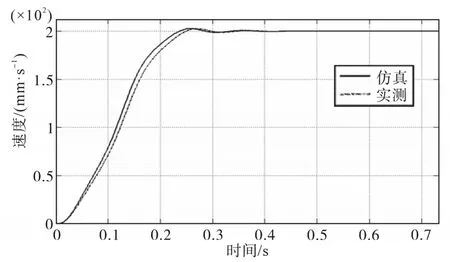
图7 电机ADRC加载仿真与实测曲线Fig.7 Simulation and measured curves of motor ADRC loading

控制电缸加载至被测样件最大全行程43 mm，设置200 mm/s的目标速度值，使用ADRC算法前后电缸加载位移随加载时间变化曲线如图8所示。由图8可得，无算法控制的电缸需要0.464 s才能完成43 mm的加载位移，但是此时电缸加载速度仅为185.6 mm/s，无法达到目标速度值200 mm/s；ADRC控制下的电缸需要0.328 s能够完成43 mm的加载位移，此时电缸加载速度已经达到200 mm/s，能够按照既定电缸加载策略进行电缸控制。

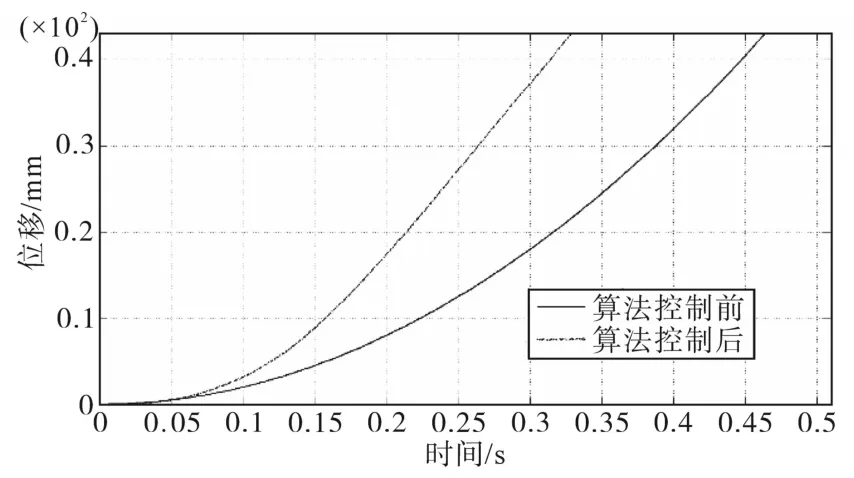
图8 200 mm/s时位移随时间变化曲线Fig.8 Curves of displacement versus time at a velocity of 200 mm/s

将电缸目标加载速度分别设置为20 mm/s，40 mm/s，60 mm/s，80 mm/s，100 mm/s，120 mm/s，140 mm/s，160 mm/s，180 mm/s，200 mm/s，分别记录PID，ADRC算法电缸加载位移达到43 mm时电缸运动所用时间。具体数据如表1所示。

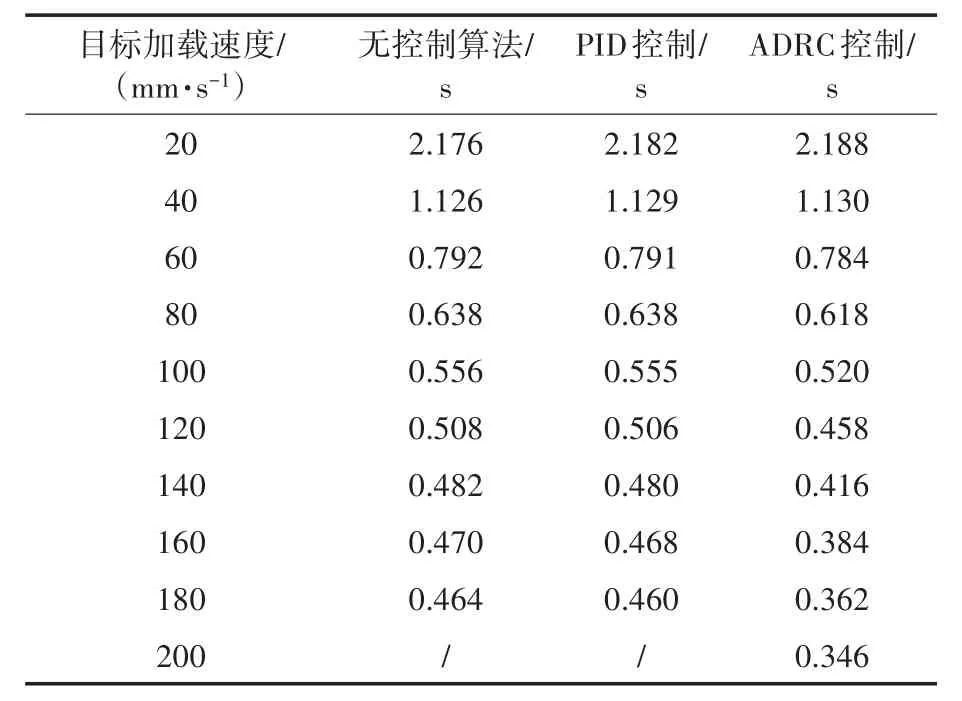
表1 不同控制算法不同速度加载到指定位移所需时间统计表Tab.1 Statistical table of time required to load to specified displacement at different target speeds under different control algorithms

根据表1数据分析可得：加入ADRC算法后，电缸能实现小位移高速度的加载动作，且以相同较大加载速度完成43 mm的加载运动时，ADRC算法下的电缸所耗时间较短，电缸加速过程得到优化，速度变化曲线平滑无速度突变。当目标加载速度大于60 mm/s时，ADRC控制下的电缸加速优化效果与目标加载速度成正比，即目标加载速度越大，ADRC算法控制的电缸速度提升越快。

4 结论

使用ADRC自抗扰控制系统控制伺服电动缸加载，相比于未加入ADRC算法，以相同大加载目标速度完成43 mm的加载运动时，ADRC控制下的电缸所耗时间较短，且以加载速度200 mm/s完成43 mm的加载运动时，ADRC控制下的电缸所耗时间仅0.328 s。试验结果表明，自抗扰算法控制下的电缸加载系统动态稳定性能较好，选用ADRC自抗扰控制算法使电动缸运动加速用时更短，可实现较小行程下的快速电缸加载，达到测试系统要求。