双三电平光伏逆变器的拓扑与控制策略研究

王宝基，张兴，曹仁贤

（1.可再生能源接入电网技术国家地方联合工程实验室（合肥工业大学），安徽 合肥 230009；2.阳光电源股份有限公司，安徽 合肥 230088）

近年来，光伏并网发电作为太阳能利用的一种重要形式得到了迅速的发展，其中大功率地面光伏电站以及分布式光伏电站占据光伏并网应用的主导地位[1]。

在大功率地面光伏电站中，三相单级集中式光伏并网逆变器以其结构简单、成本较低、易于维护等优点得到广泛应用。并且，随着对逆变器的效率、功率密度等要求越来越高，三电平逆变器拓扑已逐渐取代两电平逆变器拓扑而成为当前大功率商用光伏逆变器的主要选用拓扑。此外，为提高整个系统的电力传输效率，逆变器通常需并联后通过升压变压器接入中压电网，典型方案为两台500 kW（或630 kW）光伏逆变器并联后通过一台1 MV·A（或1.25 MV·A）双绕组变压器接入10 kV或35 kV电网[2]。既然该逆变器并联方案中变压器不可或缺，则可尝试将该方案改进为开绕组变压器双逆变器方案（简称开绕组双逆变器方案）。

开绕组双逆变器方案最早由日本学者I.Takahashi和Y.Ohmori[3]于1989年提出，其最初是应用于电机驱动领域，将电机定子绕组N线打开，分别在绕组两端串接两台逆变器，由两台逆变器共同驱动电机。通过适当地控制与调制，两台N电平逆变器可等效为一台（2N−1）电平逆变器，因而可以输出更低的谐波，减小电机转矩脉动。此外，相比于传统（2N−1）电平逆变器双N电平逆变器具有更多的冗余矢量，恰当地选取这些矢量，可以实现诸如共模电压抑制、降低开关损耗等目标。且双N电平逆变器具有比传统（2N−1）电平逆变器更高的直流电压利用率，还具有高冗余性和容错性等优势。鉴于开绕组双逆变器的这些优点，自该拓扑提出以来，已被扩展至多种应用领域，如应用于有源滤波器[4]、静止同步补偿器[5]、动态电压恢复器[6]、风力发电[7]以及光伏并网发电[8]等。当将该拓扑应用于光伏并网发电领域时，需要研究的问题主要有双逆变器拓扑的选择、独立或共直流母线（两路或单路光伏阵列供电）方案的选择、滤波器的选择、系统控制方案以及调制策略的设计等。

针对上述问题，国内外已有一些文献提出相关方案。文献[8]提出一种方案，其拓扑采用双两电平逆变器，单路光伏阵列供电，并给出一种可实现两逆变器功率均分的控制策略，该方案的不足之处很明显，系统中存在两台逆变器但仅能实现单路最大功率跟踪（maximum power point track⁃ing，MPPT），显然不利于获取更高的发电量。文献[9]给出的方案同样是采用双两电平逆变器拓扑，但两逆变器各接一路光伏阵列，从而可实现两路功率跟踪，然而其给出的控制与调制策略需要两逆变器的直流电压相等，因此两逆变器依然无法实现独立MPPT以获取更高的发电量。文献[10]所提方案主电路部分与文献[9]相同，不同之处为所采用的控制方案可实现两逆变器直流电压独立控制，即可实现两路光伏阵列的独立MPPT，但所提调制方案直流电压利用率较低，限制了逆变器MPPT工作范围。此外，文献[8−10]所提方案中均采用单电感滤波，因此需较大感值才能使并网电流满足谐波要求，这不仅增加了滤波器的体积和成本，而且也会影响逆变器的动态响应速度。为减小滤波器感量和体积，采用高阶滤波器更为合理。文献[11]提出一种应用于开绕组双逆变器的LCL滤波器方案，但其结构复杂，仍有改进空间。

综上所述，现有应用于光伏并网领域的开绕组双逆变器方案无论是主电路结构还是控制策略的选择都仍存在可改进之处，值得进一步探索和研究。为此，本文在当前已广泛商用的两逆变器并联方案的基础上，提出一种新型的开绕组变压器双三电平光伏并网逆变器拓扑。首先给出拓扑的改进思路，最终确定所提开绕组双逆变器拓扑的结构；然后建立开绕组双逆变器的数学模型，在此基础上提出一种适用于开绕组双逆变器系统的控制方案并确定合适的调制策略；最后，通过仿真和实验验证所提方案的可行性。

1 双三电平逆变器拓扑

图1为当前广泛商用的两逆变器并联方案光伏发电系统拓扑结构图。图1中，两台单级式三电平逆变器直流侧各接一路光伏阵列，通过控制可实现两逆变器的独立MPPT，交流侧各接LC滤波器，并联后通过双绕组变压器接入中压电网。

图1 两逆变器并联方案光伏发电系统拓扑结构Fig.1 Topology structure of photovoltaic power generation system with two inverter parallel scheme

在该并联方案中，变压器漏感通常作为网侧电感，与逆变器所接LC滤波器共同构成LCL滤波结构。变压器漏感值的大小与变压器阻抗电压有关，其关系式如下：

式中：Lt为变压器漏感值；vg为变压器相电压有效值；f0为基波频率；Prated为变压器额定容量；Vk为变压器阻抗电压值，对于大功率光伏用升压变压器而言，其阻抗电压值Vk一般不小于6%[8，12]。

当将并联方案改进为开绕组方案时，变压器高压侧绕组仍以星接或角接方式接入电网，而变压器的低压侧绕组中性点需打开，两端各接一台逆变器。在此方案下，两逆变器交流侧经变压器低压侧绕组串接在一起，变压器低压侧电压为两逆变器交流输出电压之差，当两台逆变器的调制波互为反相时，两台逆变器在变压器低压侧上的合成电压可达最大，为单台逆变器输出电压的2倍。为使逆变模组改动最小，两逆变器仍为原来的功率等级，其交流输出额定电流保持不变，此时需将开绕组变压器的低压侧相电压等级提高为原来的2倍。

实际上，抑制两逆变器之间的环流也可以从环流路径入手，例如通过减小光伏电池板对地分布电容也可减小环流。文献[13]详细分析了光伏电池板对地分布电容的组成和影响因素，指出常规光伏组件分布电容主要是电池元与铝边框之间的电容，而铝边框出于安全原因必须要接地，因而导致电池板对地分布电容较大，如果光伏组件无铝边框，则可极大地减小电池板对地分布电容。分析现有各类型光伏组件，双玻组件[14]的正反面盖板均为玻璃，四周无边框，因此，在开绕组双逆变器光伏发电系统中可采用双玻组件来减小电池板对地分布电容，从而抑制环流。

对于开绕组双逆变器的滤波器选择，应考虑双逆变器共滤波这一特性，原两逆变器并联方案采用的是独立LCL滤波器，需进一步改进。文献[11]提出一种LCL滤波器配置方案，两逆变器各接一组桥臂电感后，接同一组滤波电容的两端，然后通过开绕组变压器接入电网。若采用此滤波方案，并结合上面的分析，则可得到本文提出的开绕组双逆变器方案，系统拓扑如图2所示。

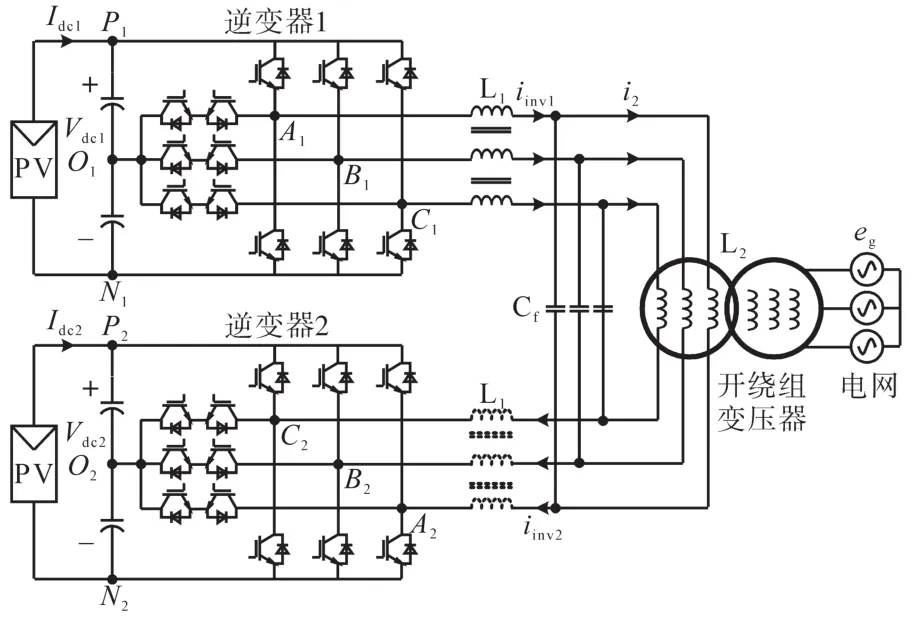
图2 开绕组变压器双三电平逆变器光伏发电系统拓扑Fig.2 Topology of photovoltaic power system with open-end winding transformer dual three level inverter scheme

根据图2可以推导出逆变器和滤波器的单相等效电路，如图3所示。图3中，vinv1，iinv1分别为逆变器1的相电压和相电流；vinv2，iinv2分别为逆变器2的相电压和相电流；L1为桥臂电感；Cf为滤波电容；L2为网侧电感，其值等于换算至变压器低压侧的等效漏感；eg为变压器低压侧相电压；i2为变压器低压侧电流。

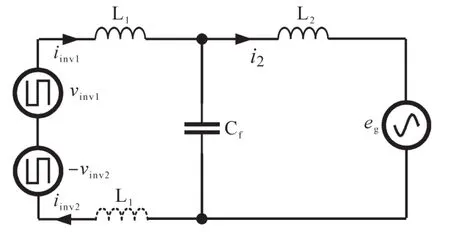
图3 逆变器和滤波器单相等效电路Fig.3 Single-phase equivalent circuit of the inverter and filter

从单相等效电路图中可以发现，两逆变器所接的两桥臂电感实际上是串联关系，因此完全可将这两个电感合为一个电感，从而节省一个磁芯，进一步降低滤波器体积和成本。相比于文献[11]提出的采用磁集成技术来减小两桥臂电感磁芯体积的方案，本文所提方案显然更易于实现。

比较所提开绕组双逆变器方案与原两逆变器并联方案，可以发现开绕组双逆变器方案的优势在于可以减小滤波器的体积和成本。首先，相比于两逆变器并联方案，开绕组双逆变器合成的输出线电压电平数增加，电压谐波降低，因此可降低滤波要求；其次，除变压器外，开绕组双逆变器方案仅需一组桥臂电感和一组滤波电容，无源器件更少；最后，开绕组变压器的低压侧电压为原双绕组变压器的2倍，且变压器阻抗电压不可改变，则由式（1）易知，其换算到低压侧的漏感值将为原来的4倍，则可进一步降低其他滤波元件的用量。

2 双逆变器系统建模

由第1节知，本文提出的开绕组双逆变器方案需要实现两路独立MPPT，即可独立控制两逆变器直流电压，并且双逆变器输出合成电压应为单台逆变器的两倍。为实现这一控制目标，需先对系统进行建模，并根据模型及相关系统参数推导两逆变器调制信号的表达式，为系统控制策略的设计提供基础。

在对图2所示的开绕组双逆变器光伏发电系统进行建模时，为便于分析，忽略线路中的电阻以及滤波电容，并将系统参数全部归算至变压器低压侧。

当系统运行在稳定状态时，定义逆变器k的x相调制波mxk为

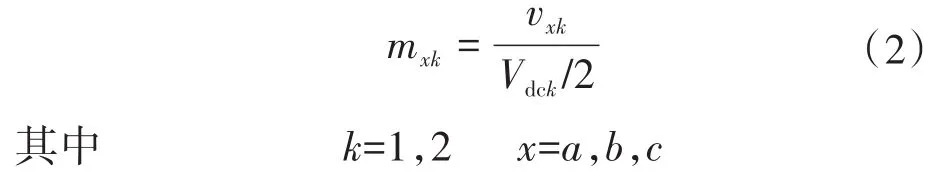
式中：vxk为逆变器k的x相交流输出电压的基波分量；Vdck为逆变器k的直流侧电容电压。

在三相静止坐标系下，根据图2，系统的交流电压方程可以表示为

式中：va，vb，vc为双逆变器交流合成相电压；ia，ib，ic为交流电流；ea，eb，ec为变压器低压侧相电压；L为交流侧总电感。

对式（3）进行Clark和Park变换，可以得到同步旋转坐标系下的表达式如下：

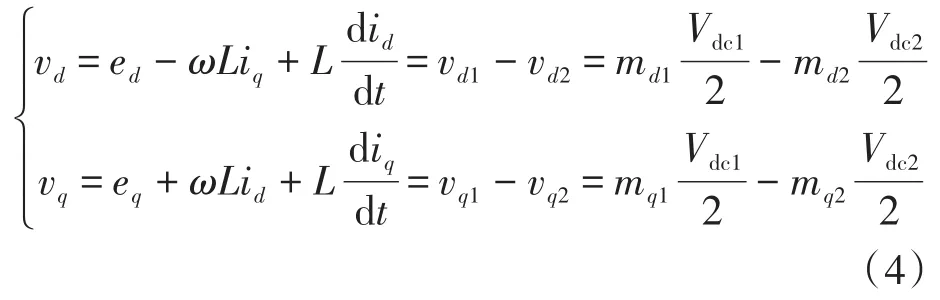
式中：vd，vq分别为双逆变器交流合成相电压在同步旋转坐标系下的d，q轴分量；id，iq和ed，eq分别为交流电流和变压器低压侧相电压的d，q轴分量；vd1，vq1和 vd2，vq2分别为逆变器 1和逆变器2输出相电压的d，q轴分量；md1，mq1和md2，mq2分别为逆变器1和逆变器2调制波的d，q轴分量。

根据式（3）和式（4）可知，双逆变器的输出合成相电压为两逆变器输出相电压之差，并且可以变换为d，q轴分量而进行分别合成。

为更直观地表征该合成关系，引入矢量对逆变器进行分析，令 v=vd+jvq，v1=vd1+jvq1，v2=vd2+jvq2，e=ed+jeq，i=id+jiq，则 v=v1− v2。由第 1 节可知本文所提方案需要双逆变器输出最大合成电压，则v1需与−v2同向。当双逆变器中各变量坐标系以电网电压定向时，eq=0，各矢量之间的关系如图4所示。

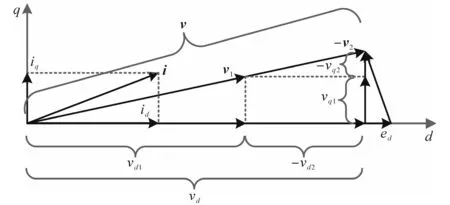
图4 逆变器运行矢量图Fig.4 Inverter operation vector diagram

根据三角形相似定理，由图4易得：

为推导 vd1，vq1和 vd2，vq2相对于 vd，vq的占比关系，还需借助于系统的功率方程。假定逆变器在工作过程中损耗为零，则两逆变器各自的输入有功功率Pdc1，Pdc2应与各自输出有功功率相等，即

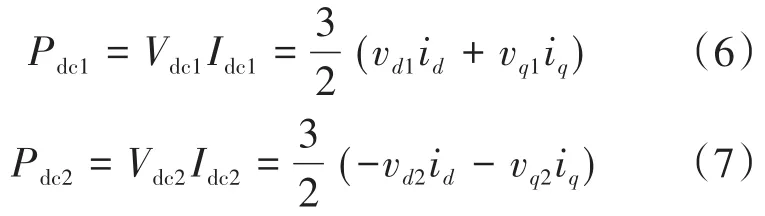
由式（6）除以式（7）并结合式（4）、式（5），可以得到关系式如下：

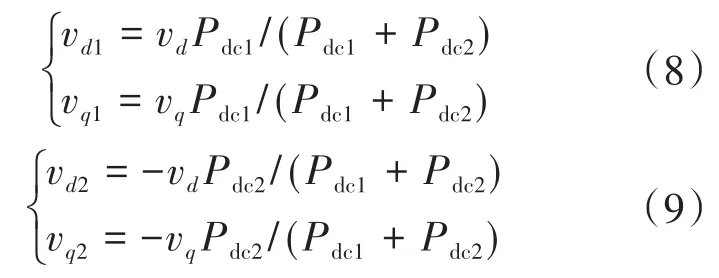
进一步地，可以得到两逆变器调制波d，q轴分量的表达式：

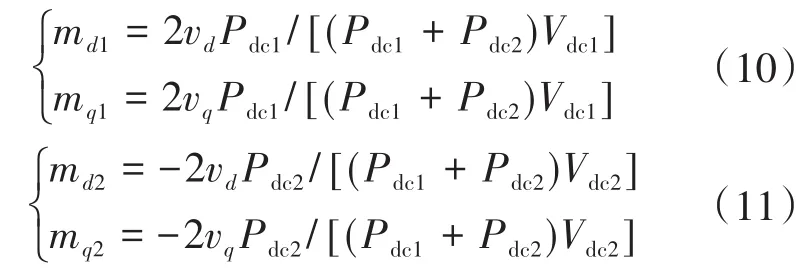
将md1，mq1和md2，mq2进行反Park和反Clark变换，即可得到两逆变器最终的调制波。

3 双逆变器系统控制方案

基于上述分析，本文给出的系统控制方案如图5所示。控制方案由3部分组成，分别为直流电压环部分、并网电流环部分以及调制策略部分，现分别对各部分进行介绍。

图5 双逆变器系统控制框图Fig.5 Control block diagram of dual inverter system

1）直流电压环部分：直流电压环的输入量为两逆变器的直流电压 Vdc1，Vdc2和直流电流 Idc1，Idc2，根据这些输入量并通过MPPT算法可得到各自的直流侧参考电压Vref1和Vref2，分别与各自的实际母线电压Vdc1和Vdc2作差后得到相应的偏差值，将偏差值经各自的PI调节器控制后得到直流电流指令值Iref1和Iref2，直流电流指令值与实际母线电压值相乘可得到两逆变器各自的直流功率指令值Pref1和Pref2，两直流功率指令值之和Pref_tot即为系统总有功功率指令。根据功率平衡关系，系统交、直流侧有功功率相等，即Pref_tot=1.5edid，则可求得直流电压环输出的系统有功电流指令值为idref=Pref_tot/（1.5ed）。

2）电流环部分：电流环的输入量为有功、无功电流指令idref，iqref以及有功、无功电流实际值id，iq。其中，idref通过直流电压环的输出得到，iqref按逆变器需求给定，当逆变器以单位功率因数并网控制且采用桥臂电流反馈时，一般取值为滤波电容上流经的无功电流，id和iq由桥臂电流值经坐标变换得到。在该环中，首先将 idref，iqref分别与 id，iq作差，再依次经各自PI调节器，电流前馈解耦环节，网侧电压前馈解耦环节后，最终得到双逆变器输出合成电压参考指令的d，q轴分量vdref，vqref。

3）调制策略部分：双逆变器的常用调制策略有统一调制和解耦式调制。统一调制是将两个逆变器看作一个整体来进行调制，常用于两逆变器直流电压和功率（或调制度）均相等的情况。对于本文提出的双逆变器方案，由于两逆变器需实现独立MPPT控制，故两逆变器的功率（或调制度）和直流电压不相等是常态，这种情况下双逆变器适合采用解耦式调制，即将双逆变器总的调制信号分为两部分，由两逆变器分别进行独立调制。本文控制方案中的调制策略环节具体为：首先由并网电流环的输出得到双逆变器输出合成电压参考指令 vdref，vqref，然后根据式（10）和式（11），将该参考指令按各逆变器有功功率占比进行分配并与直流电压解耦，得到两逆变器各自的调制波信号md1ref，mq1ref和 md2ref，mq2ref，再 通 过 反Park变换和反Clark变换，进一步获得两逆变器在静止坐标系下调制信号 ma1，mb1，mc1和 ma2，mb2，mc2，并最终经过独立的空间矢量（SVPWM）调制产生驱动两逆变器的PWM信号。

4 仿真分析

为了验证所提方案的正确性，在Matlab/Simulink平台下搭建所提开绕组双逆变器方案的仿真模型进行仿真研究，且为与实验平台相统一，采用电压源串接电阻来模拟光伏阵列，系统仿真参数如下：双逆变器额定功率30 kW，单台逆变器额定功率15 kW，开关频率5 kHz，直流电源电压660 V，直流串接电阻1.6 Ω，滤波电感2.4 mH，滤波电容5 μF，开绕组变压器变比364/380，电网线电压380 V。

图6为开绕组双逆变器在两逆变器功率平衡运行模式下的线电压仿真波形，从上至下依次为逆变器1线电压vA1B1的波形、逆变器2线电压vA2B2的波形以及双逆变器合成线电压（vA1B1−vA2B2）[10]的波形。从图6中可以发现，单台三电平逆变器的线电压为5电平，而双三电平逆变器的输出合成线电压为9电平，与传统五电平逆变器的输出线电压电平数相等，即双逆变器输出线电压具有更低的谐波，因此可以降低滤波要求，节省滤波成本。

图6 各逆变器线电压及双逆变器合成线电压仿真波形Fig.6 Simulation waveforms of the line voltage of each inverter and the combined line voltage of the dual inverter

图7为开绕组双逆变器在直流电压指令变化时两逆变器直流电压、直流功率和并网电流的仿真波形。初始时两逆变器的直流电压指令值均为621 V，此时两逆变器功率均衡运行，有功功率均约为15.14 kW。在0.05 s处，逆变器1直流电压指令值突变为640 V，此时，逆变器1有功功率变为8 kW，系统总有功功率减小为约23.14 kW，并网电流幅值也相应减小。在0.1 s处，逆变器2直流电压指令值突变为640 V，此时，逆变器2有功功率也变为8 kW，系统总有功功率减小为16 kW，并网电流幅值再次相应减小。仿真结果表明本文提出的控制方案可实现所提开绕组双逆变器方案的独立直流电压控制，两逆变器可实现独立的功率追踪。

图7 双逆变器直流电压给定变化时的仿真波形Fig.7 Simulation waveforms of the dual inverter when the DC voltage reference change

5 实验验证

为进一步验证本文所提方案的有效性，搭建30 kW独立直流母线开绕组变压器双逆变器实验平台，如图8所示。限于实验条件，直流侧采用两台15 kW整流器（最大可输出20 kW功率）串联电阻来作为直流源，以DSP TMS320F28377为控制芯片实现相关算法，采用高压探头700924、电流钳FLUKE i400s、电流钳CHAUVIN ARNOUX E3n以及横河示波器DLM2024进行电压和电流波形的采集与观测。实验参数和工况与仿真基本保持一致。

图8 开绕组双三电平逆变器实验平台Fig.8 Experimental platform for open-end winding dual three level inverter

图9为开绕组双逆变器在两逆变器功率均衡运行模式下单台逆变器以及双逆变器的线电压实验波形。通过实验波形可以看出，双三电平逆变器合成线电压（vA1B1−vA2B2）的波形可等效为单台五电平逆变器的线电压波形，为9个电平，实验结果与仿真结果一致，验证了双逆变器具有更低输出电压谐波这一特性。

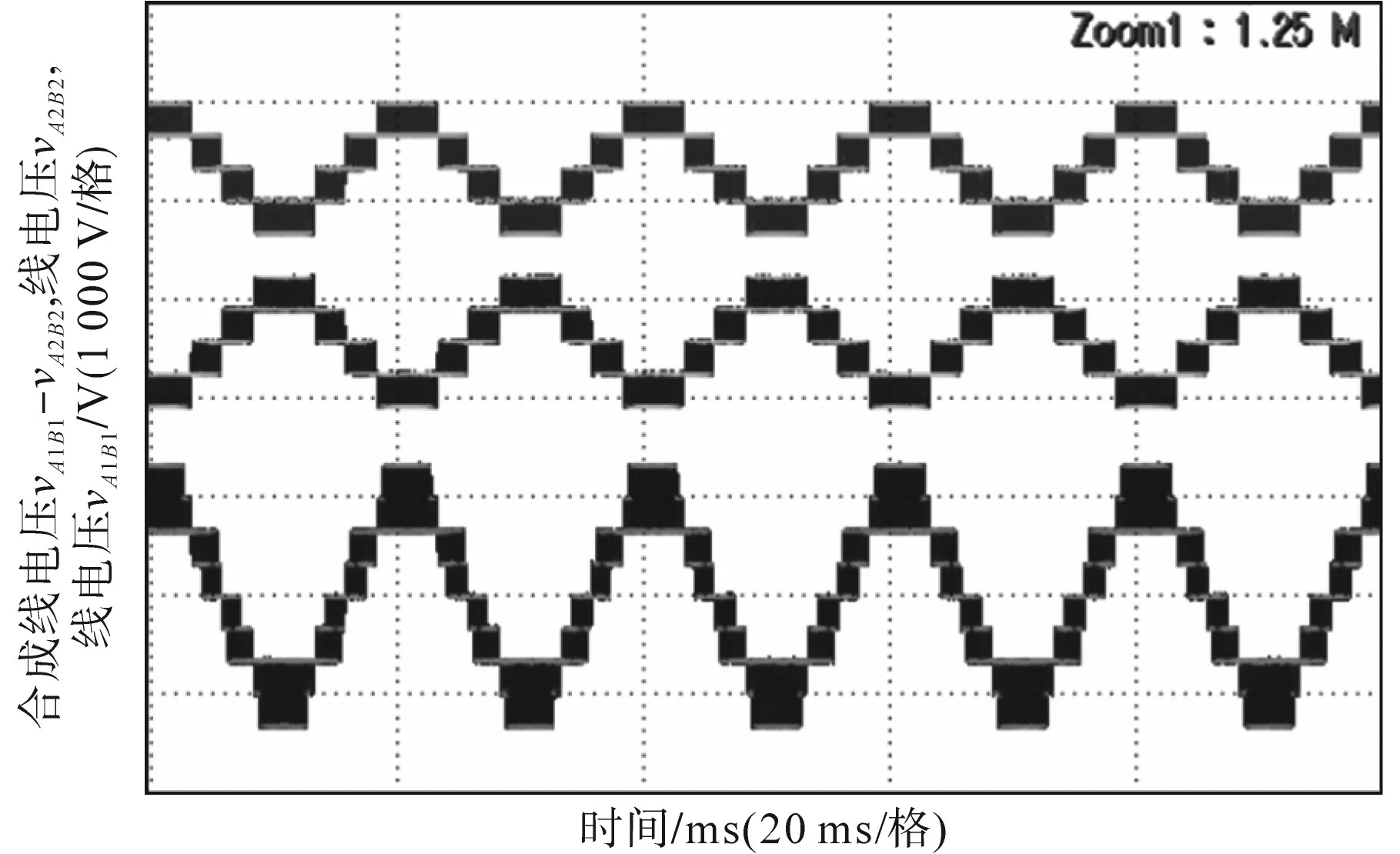
图9 各逆变器线电压及双逆变器合成线电压实验波形Fig.9 Experimental waveforms of the line voltage of each inverter and the combined line voltage of the dual inverter

图10为开绕组双逆变器系统在两逆变器直流电压指令变化时两逆变器直流电压、直流功率以及并网电流的实验波形。其中两逆变器直流功率通过程序运算得出后，再通过DSP28377的数模转换器（DAC）接口放出，然后经示波器采集得到。实验工况与仿真工况一致，初始时两逆变器均以满载15 kW功率运行，两逆变器直流电压均约为621 V，并网电流幅值约为39 A。在t1时刻，逆变器1直流电压指令突变为640 V，逆变器1直流电压快速跟上指令，其功率变为约8 kW，并网电流幅值减小为约30 A。在t2时刻，逆变器2直流电压指令突变为640 V，逆变器2直流电压快速跟上指令，其功率变为约8 kW，并网电流幅值减小为约20 A。实验结果显示双逆变器可实现两直流电压独立控制，证明了所提双逆变器方案及控制策略的有效性。

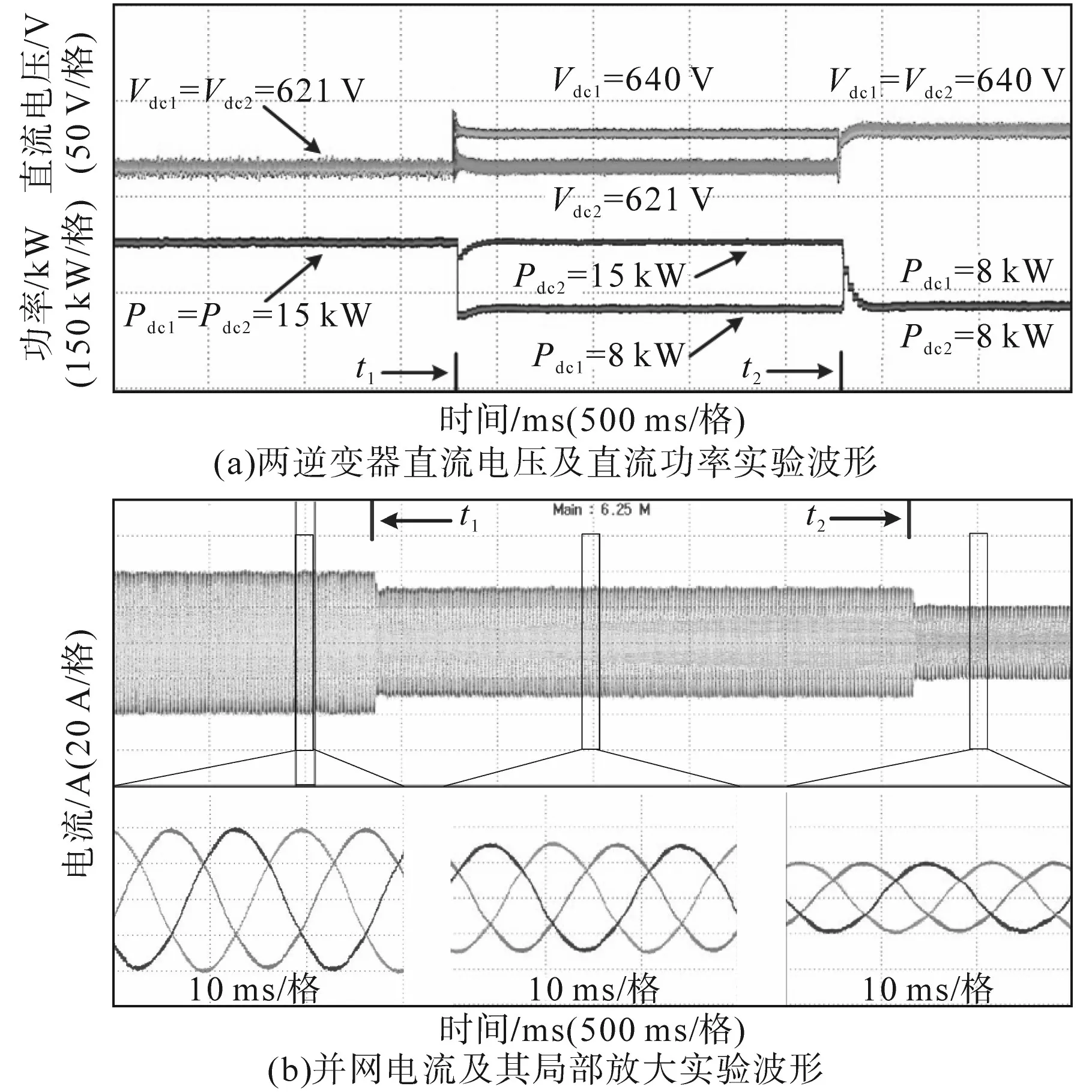
图10 双逆变器直流电压给定变化时的实验波形Fig.10 Experimental waveforms of the dual inverter when the DC voltage reference change

6 结论

本文研究了开绕组双逆变器拓扑应用在光伏并网发电领域的拓扑结构及控制策略。首先分析了现有方案的优缺点，指出现有方案仍有改进空间，值得进一步探索。进而从当前已广泛商用的两逆变器并联方案入手，探索将其调整为开绕组双逆变器方案的改进思路，提出了一种基于开绕组变压器双三电平逆变器拓扑的光伏并网发电系统方案，并指出所提方案的优势在于可以减小滤波器的体积与成本。此外，还分析了开绕组双逆变器拓扑的数学模型，并基于此提出了一种可实现双逆变器独立MPPT功能的控制策略。最后，通过仿真和实验验证了所提方案的正确性和可行性。滤波器的参数设计方法以及与现有方案的比较分析将是本文下一阶段研究内容。