快速路匝道瓶颈特性与临界流率模型

李宏海,盘意伟,王 昊

(1.交通运输部公路科学研究所智能交通技术交通行业重点实验室,北京100088;2.佛山市城市规划设计研究院,广东 佛山528010;3.东南大学交通学院,江苏 南京210096)

引 言

快速路汇入匝道合流区是城市快速路网的主要瓶颈区域,由于匝道交通流量的汇入,导致高峰时段拥堵现象频发,严重影响了快速路的整体运行效率。匝道汇入车辆对主线的干扰导致主线交通的流率、速度急剧下降,该现象称为交通瓶颈的崩溃现象(breakdown)。交通崩溃现象已成为当前交通流理论研究领域和交通工程领域的热点问题。目前,对匝道瓶颈的交通崩溃问题的研究主要以基于实测数据的经验模型为主。Banks[1]对美国圣地亚哥高速公路的多个瓶颈点的观测数据进行了分析,发现匝道流率是引起交通流崩溃的关键因素。Shawky等[2]基于高速公路匝道合流区的观测数据建立了交通崩溃概率与流量、占有率之间的关系模型,发现不同瓶颈处发生交通崩溃的概率均服从韦伯分布,加速车道长度、合流流率比对交通崩溃概率有明显影响。李林恒[3]、谢东岐等[4]基于国内快速路实测数据研究了breakdown现象,并提出了相关模型。然而,这些经验模型来源于对统计结果的分析,没有对匝道合流区复杂的驾驶行为和交通流运行特性进行深入的研究,无法解释交通崩溃现象的发生机理。本文从微观角度研究匝道车辆汇入行为对主路交通的影响,以跟驰理论与交通波理论为基础,分析了匝道瓶颈拥堵形成机理,并构建了主路与匝道临界流率模型,为快速路的匝道流量管控提供理论基础。

1 数据采集与分析

1.1 数据采集

为了分析快速路汇入匝道的瓶颈特性,本文选取了广州市内环路、东风路两条快速路上的南岸匝道、西场匝道、黄沙匝道、先烈匝道以及恒福匝道5个典型汇入匝道瓶颈点进行了视频观测。所选择的汇入匝道附近的主线道路线形均为平直路段,并且远离下游匝道,保证瓶颈处的拥堵是由匝道汇流直接造成的原发性拥堵,有利于后续对拥堵机理的深入分析。对瓶颈点的数据采集工作安排在2014年5月的5个工作日进行,观测时间为每天7:00至10:00,16:00至19:00,涵盖了早晚高峰时段,并在高峰时段前后各延伸30 min的观测时间,以便完整记录瓶颈点交通流由畅行至拥堵再至恢复畅行的演变过程。利用AUTOSCOPE视频分析系统以30 s统计间隔对调查视频进行数据提取,采集的参数包括匝道合流区主线车道和加速车道的流率、速度、密度和车头时距等。

1.2 数据分析

1.2.1 合流区拥堵特性

基于观测数据,可以研究在一次完整的交通流崩溃现象中,合流区车速演变过程及其与主线、匝道交通流率之间的关系。本文所观测的5个典型汇入匝道瓶颈点的交通崩溃现象具有相同的规律,限于篇幅此处以西场匝道的数据为例进行介绍。由图1可知,在一次交通流崩溃事件中,合流区主线车道速度经历了由高位值(大于50 km/h)骤减至低位值(10-20 km/h),持续一段时间后又重新恢复到高位值(大于40 km/h)的变化过程。

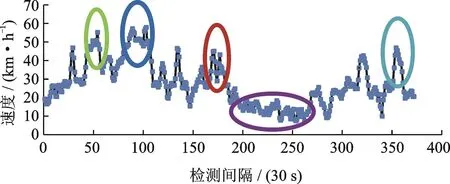
图1 西场匝道合流区交通崩溃过程车速时变图

在车速时变图中选择5个典型的速度检测区间(如图1中的圆圈所示),研究在当前速度区间下,对应的主线和匝道交通流率水平的分布规律,如图2所示。

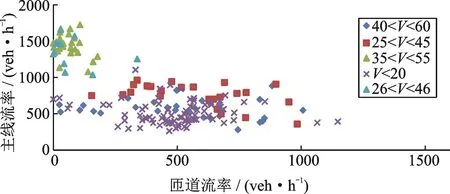
图2 西场匝道合流区车速与主线、匝道流率关系图

图1中紫色圆圈内数据和图2中紫色X形数据为交通崩溃期间的数据。结合图1和图2可知,在远离交通崩溃发生的第50个检测间隔和第350个检测间隔附近,交通流处于畅行状态(26 km/h＜V＜55 km/h),匝道流率在0-200 veh/h,主线外侧车道流率在1000-1700 veh/h。在交通崩溃发生前,速度曾出现小幅下降,其两侧对应两个速度小高峰(图1中的红色圈和蓝色圈区域),此时交通流同样处于畅行状态(25 km/h＜V＜60 km/h),主线外侧车道流率分布在500-1000 veh/h范围,但匝道流率变化范围非常广,在0-1000 veh/h之间,说明在此阶段,匝道交通需求急剧增加,频繁的匝道车辆汇入最终导致了交通流崩溃的发生。在交通崩溃发生后,合流区交通流进入了拥堵状态,速度和流量参数都保持在一个稳定的水平,其中速度分布在10-20 km/h区间内,主线流率分布在300-700 veh/h区间内,匝道流率主要分布在400-600 veh/h区间内。

总体上看,交通崩溃发生后,合流区速度大幅降低,降幅为40 km/h;合流区总流量最大值明显降低,由约1500 veh/h降低到约1300 veh/h,降幅为13%,该结论与以往的研究结果相一致。大量的研究表明,交通崩溃现象会导致通行能力下降,降幅范围为5%-18%[5]。

1.2.2 瓶颈识别

从交通流长期运行特征来看,瓶颈处发生交通崩溃现象是概率事件;而对于给定交通场景、交通状态,交通参数与交通崩溃现象之间存在确定的关系[6]。对交通崩溃现象的识别有三种具有代表性的方法:转换累计曲线法、阈值判别法和模糊集法。转换累计曲线法由Cassidy等[7]提出,通过平移得到相邻断面累计流量间横、纵向偏移,从而确定瓶颈的产生时刻和位置;阈值判别法以一个或多个交通流参数为指标来识别交通流交通崩溃,Das等[8]、Daganzo等[9]、Hall等[10]分别以速度、密度、密度与流率的比值为指标识别交通崩溃的发生;模糊集法基于Kerner[11]的三相交通流理论,采用基于规则的模糊集理论识别交通流状态的转变。这些方法中,转换累计曲线法识别效率低且计算机可操作性差;模糊集法其规则的制定对数据依赖性太强,对不同瓶颈点其规则需要调整;阈值判别法操作简单,便于自动化处理,只要阈值组合选择得当,即可准确判断交通崩溃的发生[12]。因此,本文根据AUTOSCOPE数据提取结果,选定连续10 min空间平均速度低于30 km/h,并且密度高于60 veh/km时则认为瓶颈处发生了交通流的崩溃现象。图3为南岸汇入匝道瓶颈点在2014年5月26日下午的速度、密度时变图,根据本文选定的速度、密度阈值识别到从当天下午的第90个检测间隔起发生了一次交通崩溃现象,由此引发的拥堵持续了约25 min。

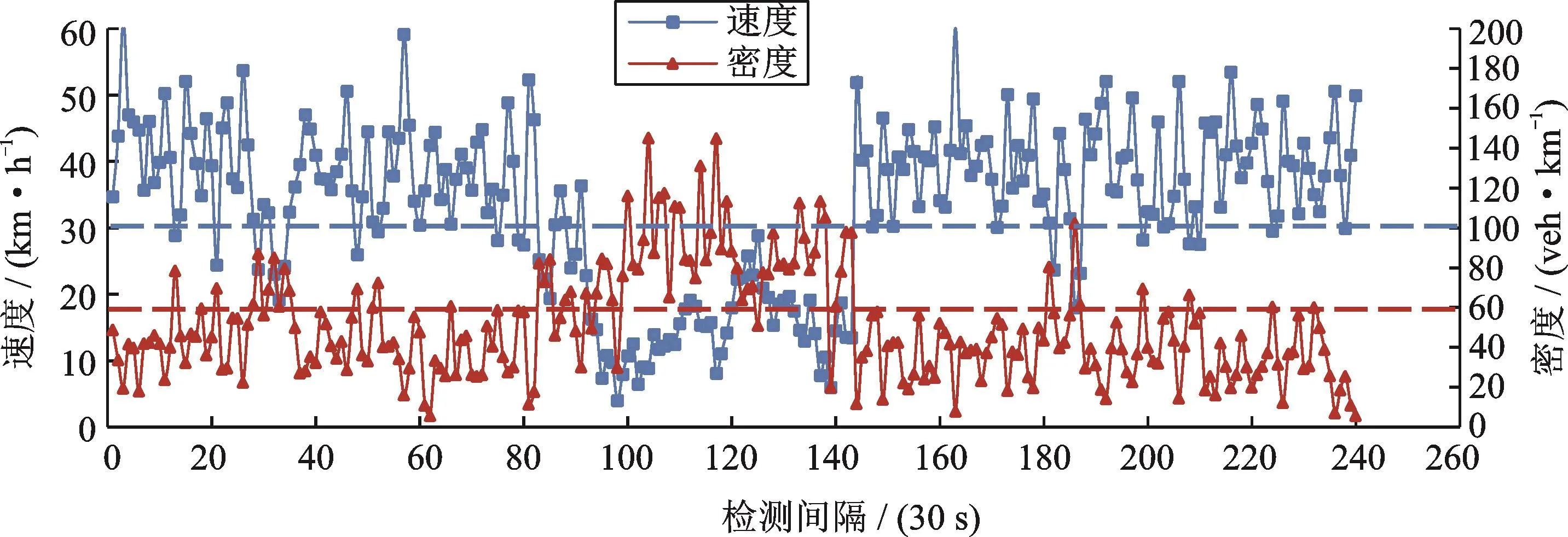
图3 汇入匝道瓶颈交通崩溃现象识别图

在快速路汇入匝道合流区,由于匝道车流持续的汇入影响,一辆匝道车辆的强行汇入或者多辆匝道车辆的成簇汇入可以使交通流在中等流量水平下发生崩溃现象。而匝道车辆强行汇入或者成簇汇入的发生概率与匝道交通流率和主路交通流率存在密切的联系,因此在识别到一次交通崩溃现象发生后,同时记录下在交通崩溃发生前5 min内合流区内主线车道和匝道的平均流率,用以表征引发本次交通崩溃现象的“主线-匝道”流量组合。图4为本次调查的5个典型匝道瓶颈在交通崩溃发生前的“主线-匝道”流率散点图。由图可知,导致交通崩溃发生的主路外侧车道流率与匝道流率之间存在明显的负相关关系,即匝道流率越大,主线爆发交通崩溃的临界流率就越小。

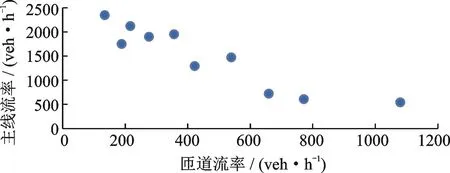
图4 交通崩溃发生时主线流率与匝道流率实测数据散点图

2 临界流率模型

通过对所采集交通流视频的分析,发现匝道合流区拥堵形成的一般过程如下:当主线车辆处于跟驰状态时,相对低速的匝道车辆汇入主线后,后随的主线车辆会依次采取减速动作,形成减速波。每一辆由匝道汇入主线的车辆都会形成一个减速波,并沿着主线上游方向传递。如果车流中上一辆汇入车辆的减速波影响尚未消散即迎来了下一辆汇入车辆的减速波,那么减速波的叠加作用将会使车流的速度进一步降低,并最终导致拥堵即交通崩溃现象的形成。

2.1 Newell低阶跟驰模型及基本图

为了描述匝道车辆汇入主线过程产生的交通影响,文本应用Newell低阶跟驰模型[13]进行建模分析。Newell用线性模型刻画交通波的动态特性,模型简单且符合实际观测,因而受到广泛的应用。该模型认为驾驶者在跟驰过程中,总是按照某个固定的时间延迟τn和空间位移d n复制前车的行驶轨迹,从而形成稳定速度的交通波。Newell模型的跟驰轨迹时空图如图5(a)所示。当假定交通流中所有车辆都遵循Newell模型时,可以获得如图5(b)所示的三角形交通流基本图。该三角形基本图由三个关键参数确定,自由流速度v f、拥挤态交通波速-W以及堵塞密度k j。

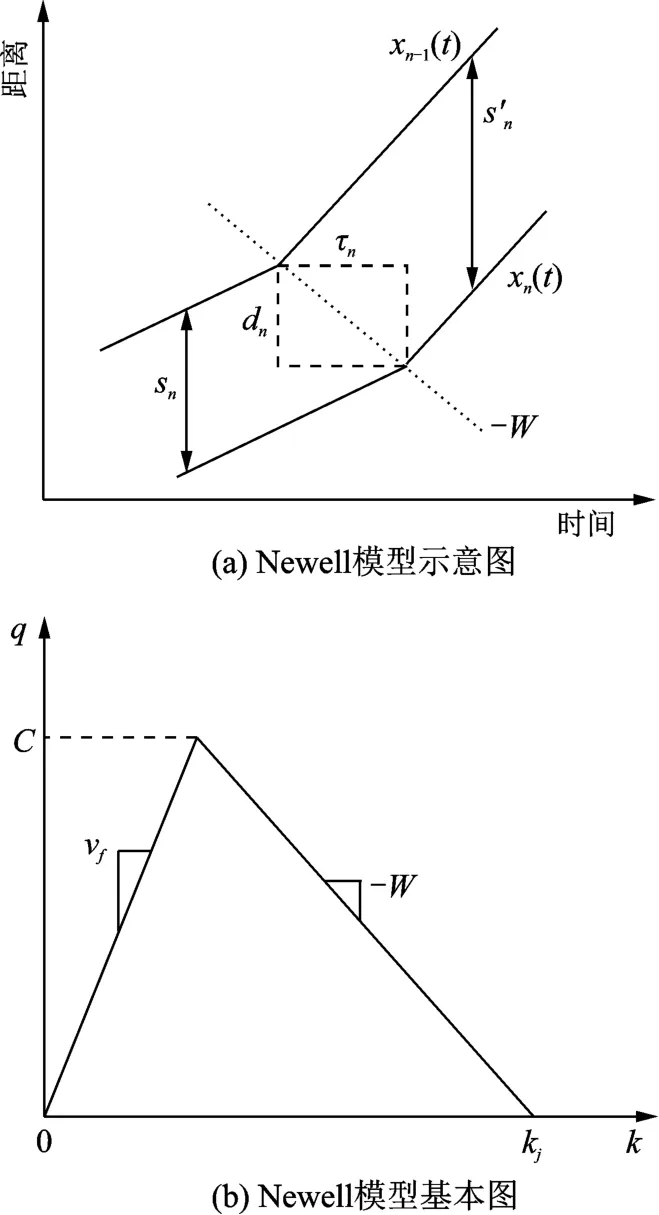
图5 低阶Newell模型的轨迹特性与基本图

2.2 交通崩溃的条件分析

如图6所示,假设主路上外侧车道一列连续车队以均衡态驶向汇入匝道合流区,速度为v1,v1＜v f。当一辆车从汇入匝道汇入,由于匝道车辆速度v2低于主路车辆速度v1,在汇入点处将产生一个减速波并向主线上游传播。经过一段时间T0的加速,汇入车辆速度提升至车速v3,此时将产生一个加速波向主线上游传播。

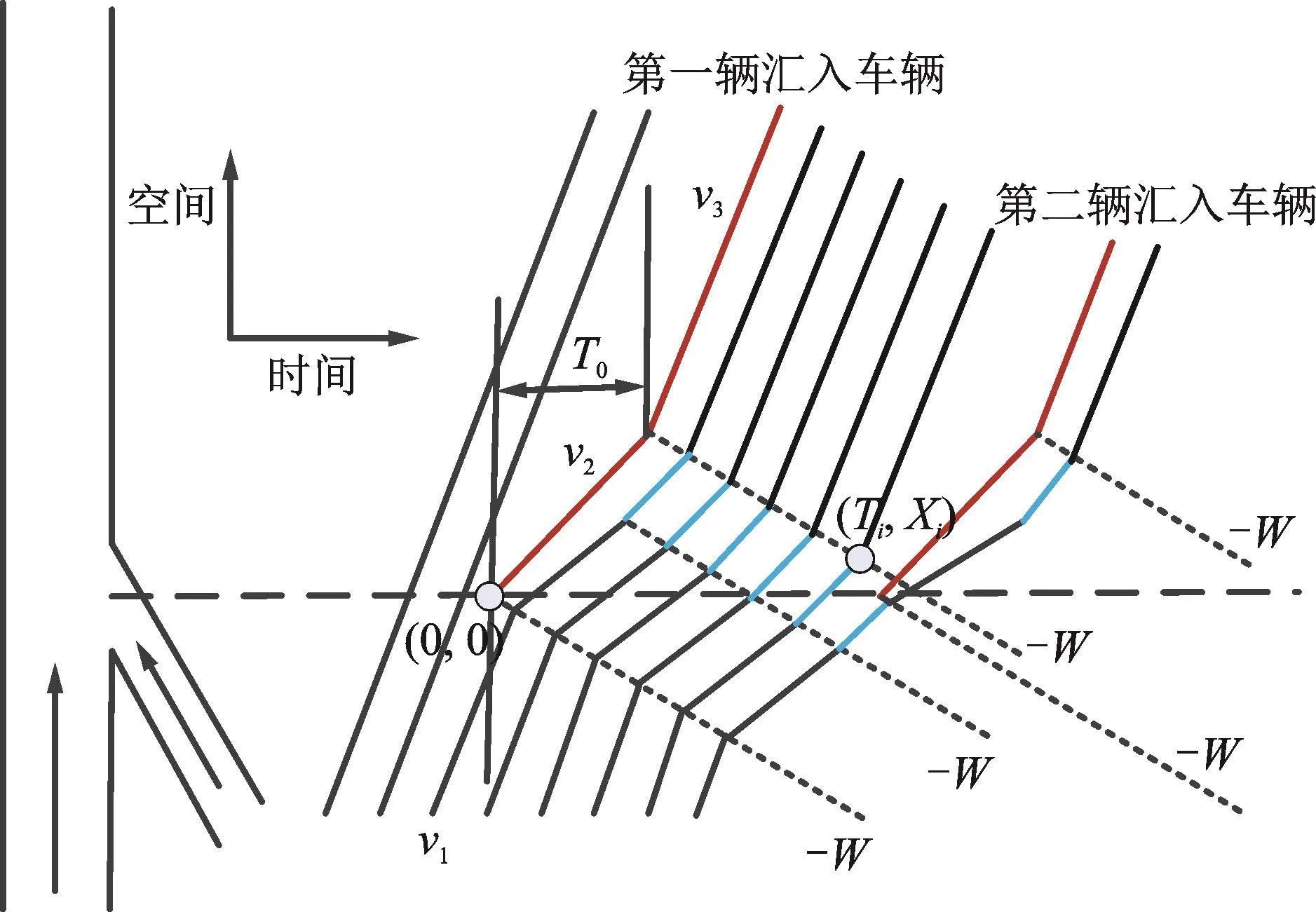
图6 匝道车流影响下的主线交通崩溃形成机理示意图

与此同时,在匝道车辆汇入时刻,受其直接干扰的主线第一辆车的跟驰间距瞬间缩短为小于平衡态的间距,使其不能按照正常的跟驰规则复制前车的变速行为,必须进一步减速以获得与汇入速度v2相适应的平衡态间距,此时该车也将产生一个加速波向主线上游传播。后续车辆都按照均衡态下的Newell模型规则,复制前车的行驶轨迹。

若以匝道汇入第一辆车的时空坐标为原点坐标(0,0),主路上第i辆车驶出扰动影响范围时的时空坐标为(T i,X i),匝道车辆的车头时距为H。则如果在H时间内,第i辆车已经驶出扰动影响范围并通过汇入匝道合流点,则扰动不扩大,交通崩溃现象不发生;否则,第二辆新增匝道汇入车辆形成的减速波将对第i辆车产生叠加影响,扰动进一步增大,并最终诱发交通崩溃现象。因此,交通崩溃现象不发生(即不会产生拥堵)的条件表达为

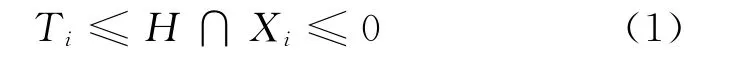
当上述条件式(1)取等号时,对应为交通崩溃的临界条件。

2.3 交通崩溃的临界流率模型

根据以上的情景分析,考虑这样一种临界条件,即在图6中第二辆匝道汇入车辆到达之前,受第一辆匝道汇入车辆减速波影响的主线车流刚好驶出扰动影响范围并通过汇入匝道合流点。此时有

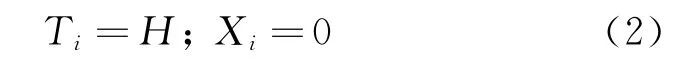
则根据图6中车流轨迹线与交通波的几何关系,不难得到临界条件(2)等价于

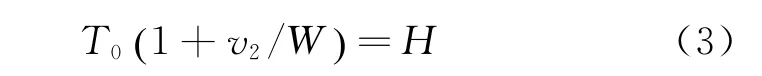
假设车辆由匝道汇入时的速度比主线交通流速度低Δv,则

将方程(4)代入方程(3),并整理得

根据图5(b)中三角形基本图模型,可以获得主线车流速度为v1时主线交通流的小时流率qm为

另一方面,由车头时距与交通流率互为倒数的基本关系可知,与匝道车辆时距H对应的匝道交通流的流率q r为

于是,将方程(6)和方程(7)代入方程(5)即可获得交通崩溃临界条件下主线流率与匝道流率的函数关系

接下来将对上述交通崩溃临界流率模型进行标定和验证。

3 模型标定

本文提出的模型共含四个参数:交通波速W、堵塞密度k j、匝道车辆加速时长T0以及匝道与主线速度差Δv。这四个参数均有明确的物理意义,均可直接通过测量获得。然而,由于本文没有足够的观测样本,无法直接测出堵塞密度和交通波速。因此,采用图4所示的实际观测获得的交通崩溃临界条件的数据对模型进行标定。

采用非线性最小二乘法搜索最优参数取值,目标函数如下

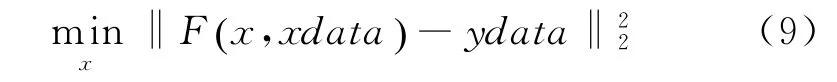
其中,x=[W,k j,Δv,T0],F(x,xdata)为方程(8)所示的临界流率函数,xdata和y data为向量,分别表示图4中交通崩溃临界条件下的实测数据点的匝道流率值和主线流率值。采用非线性最小二乘法对上述问题进行求解,各参数的初始值、可行域区间以及优化结果如表1所示。

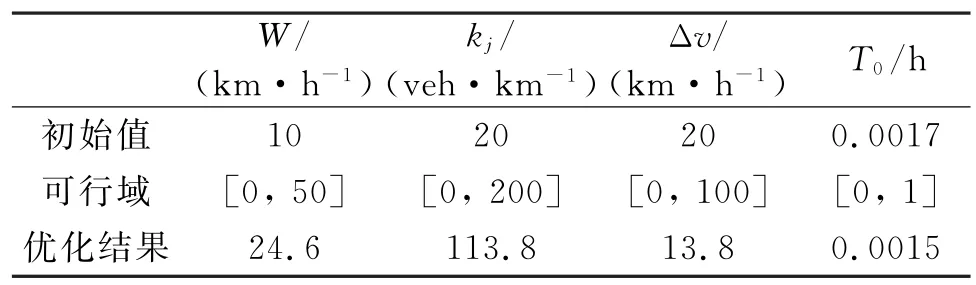
表1 交通崩溃临界流率模型参数标定结果

标定结果显示,交通波速W=24.6 km/h,堵塞密度k j=113.8 veh/km,匝道与主线速度差Δv=13.8 km/h,匝道车辆在主线的加速时间T0=0.0015 h=5.4 s。所有参数的最优解均位于可行域内部,且取值符合实测结果[14]。图7给出了标定后的模型曲线与实测数据间的对比情况。随着匝道流率的增加,诱发交通崩溃现象的主线流率临界值不断降低。总体上,本文提出的交通崩溃临界流率模型与实测数据具有很好的一致性。

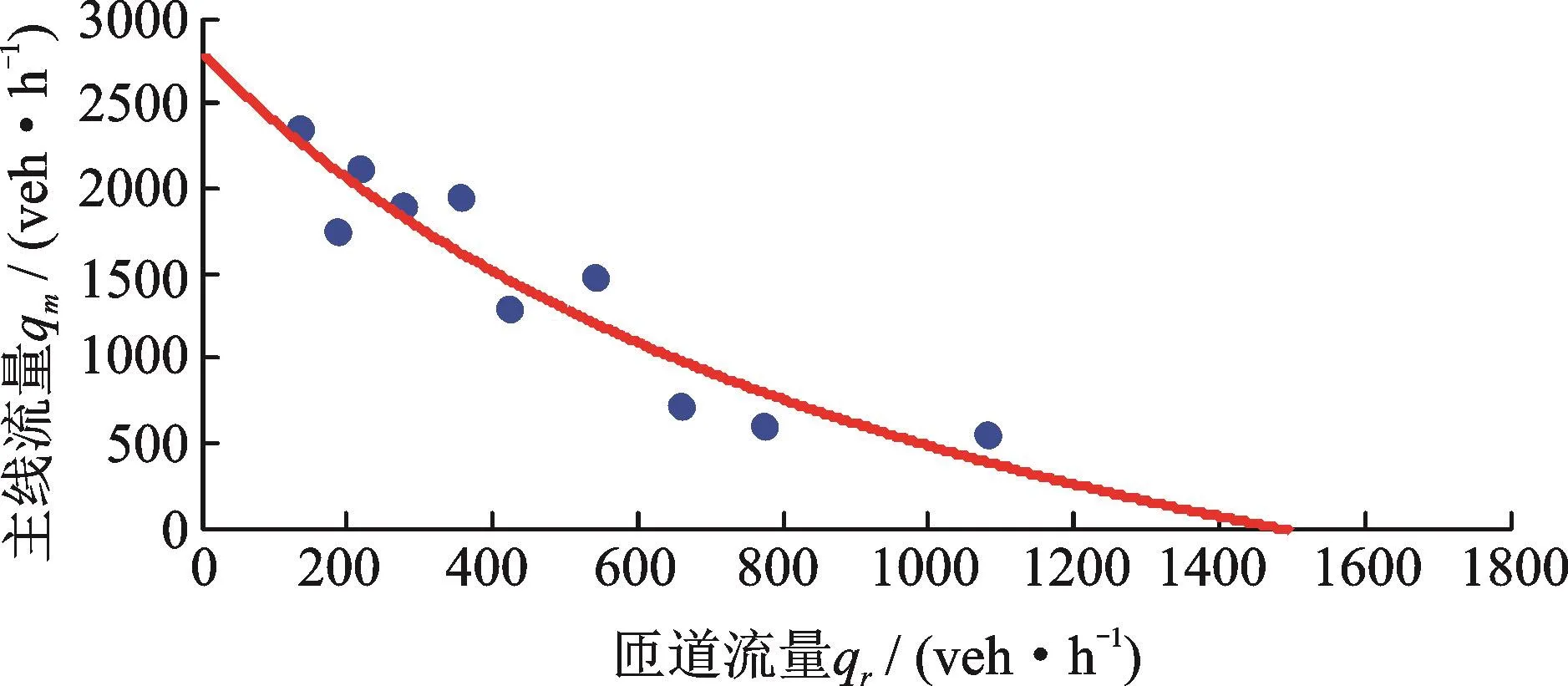
图7 交通崩溃临界流率模型曲线

4 结 语

本文应用实测数据对快速路汇入匝道合流区交通崩溃现象的特征进行了研究,基于Newell低阶跟驰模型,分析匝道车辆汇入主线过程中车辆轨迹和交通波的运动特性,提出了交通崩溃现象形成的临界条件,并建立了临界条件下主线流率与匝道流率间的关系模型。实测数据标定结果表明,该模型的参数取值在合理范围内,模型输出的结果与实测数据具有很好的一致性。不同于回归模型,文本提出的模型由交通崩溃形成机理推导而出,结构简单且所有参数都具有明确物理意义,具有很好的可移植性。需要指出的是,本文对匝道车辆做了均匀到达的假设,而实际条件下车辆到达具有一定的随机性。将随机性条件引入该模型将是下一阶段的研究方向。