数学文化视域下数学教学设计及思考
2021-10-28陈一叶
陈一叶

【摘 要】从历史的视角来看,人类创造的各种数学知识,究其本质,就是一个广泛的蕴含数学文化的知识体系。如何在小学数学设计中渗透数学文化,使学生不仅掌握数学知识,更能深刻领悟知识背后的思想和方法。教学设计要把握好三个策略:一是透视知识,充分发掘知识的文化内涵;二是厘清知识脉络,并将数学知识的相关历史融入数学教学中;三是让学生充分经历知识的再创造过程,并在其中感悟知识的文化内涵。
【关键词】数学文化 教学设计 教学策略
从历史的视角来看,人类创造的各种数学知识,究其本质,就是一个广泛的蕴含数学文化的知识体系。数学知识是人类以抽象的方式去把握世界客观规律的结果。这一过程体现人类的智慧与理性,蕴含着数学知识从产生到发展的整个过程中人类的主动性与创造性。因此,数学符号作为数学知识的载体,蕴含着丰富的文化特征。数学教学中,学生如果忽略知识的文化背景,仅仅记忆一些数学知识,不仅不能感悟内蕴于知识之中的文化内涵,也必定不能深刻理解知识的本质。
一、数学教学设计中渗透数学文化的基本策略
数学教学设计是教师对数学教学活动的预先规划,对学生已有知识经验情况的预判。教学设计是上好课的前提条件。如何在数学教学设计中进行有效的数学文化渗透?笔者以为,首先在设计时要发掘数学知识的文化内涵;其次要设计好数学知识的情境脉络;最后要让学生在知识的境脉中领悟知识的文化内涵。
(一)透视知识,发掘文化内涵
数学知识不是数学符号的堆积,数学学习也不单纯是对数学概念、定理和公式的记忆。但实际教学呈现给师生的往往是静态的知识结构,这些结构掩盖了知识长期而曲折的形成和发展过程,这个过程包括了人类在探索知识过程中的精神、数学知识背后所体现的思想方法及数学知识对人们生活的影响等。因此,从文化的视角来探寻数学知识的发展,对于数学教学有十分重要的意义。
用文化的视角来理解数学知识,关键要发掘相关知识的数学文化史。克莱因认为:历史是教学的指南。弗赖登塔尔曾说过:“儿童应该重蹈历史,尽管不是实际发生的历史,而是倘若我们的祖先已经知道我们今天有幸知道的东西,将会发生的历史。”
以圆为例。圆是基本的平面图形,看似简单却蕴含了极其丰富的内涵。从历史上看,人类对圆的认识是从圆的应用开始而逐步深入的,其中包括许多重大的发现,如圆周率、割圆术等。大约一万八千年前的山顶洞人用一种尖状的石器来钻孔,一面钻不透,再从另一面钻。石器的尖是圆心,它宽度的一半就是半径,这样以同一个半径和圆心一圈圈地转就可以钻出一个圆形的孔。
6000年前,半坡人就已经会造圆形的房顶了。古人还发现圆的木头滚着走比较省劲。后来他们在搬运重物时,就把几段圆木垫在重物的下面滚着走,这样就比扛着走省力得多。如古代金字塔的建造,古埃及人可能就是利用在巨石上装上圆轮将巨石拉上坡的。大约在6000多年前,美索不达米亚人做出了世界上第一个轮子——圆的木轮。约在4000年前,人们将圆的木轮固定在木架上,这就成了最初的车辆。
人类在生活生产中对圆的广泛应用,实际是自觉和不自觉地在应用圆的许多特性,如許多瓷器都制成圆形,是因为同样大的容积,圆形瓷器是最小的,而且相对容易制作。在2000多年前,我国的墨子给出了圆的定义:“一中同长也。”意思是说,圆有一个圆心,圆心到圆周的长都相等。这个定义抽象出了圆最本质的属性,也可以理解为古人在大量实践的基础上逐渐形成了对圆的理性认识。
圆周率的发现可以说是人类认识圆的一个里程碑。据史料记载,古代许多伟大的思想家曾致力于寻求圆周率的精确值。在众多对圆周率的探寻者中,阿基米德是第一个通过计算方法而不是测量方法得到圆周率的人。他发现当正多边形的边数增加时,这个正多边形的形状就越来越接近圆,根据这个思路,圆就相当于一个由许多极其短的边构成的正多边形,这个想法提供了计算圆周率的新途径(见图1)。如果把正六边形看作近似的圆,通过内接正六边形和外切正六边形可算得,圆周率是3<π<3.46,当正多边形边数增加到96时,就可得到3.1408<π<3.1429。我们可以发现,通过这种方法,当正多边形边数越多,算得的圆周率就越精确。
在这之后,刘徽的“割圆术”也是充分利用了内接正多边形计算出圆周率和圆面积。所谓“割圆术”,就是以“圆内接正多边形的面积”,来无限逼近“圆面积”。可见,人类在对圆逐步深入地认识的过程中,首次将极限和无穷小分割引入数学证明,成为数学史中不朽的篇章。
发掘知识的数学史是渗透数学文化的前提,圆丰富的数学文化内涵,不仅揭示了圆的相关知识的形成,更为实际的教学指明了方向。
(二)厘清脉络,实现有效融合
对内蕴于知识中的文化内涵的感悟,必须建立在学习者对相关知识的境脉的深刻理解的基础上。要让学生深刻理解知识的境脉,教师的教学设计就必须把握好两个方面:一是厘清知识的来龙去脉,明晰知识的产生和发展过程;二是要根据知识脉络进行有效的设计,使之成为适合学生学习的材料。
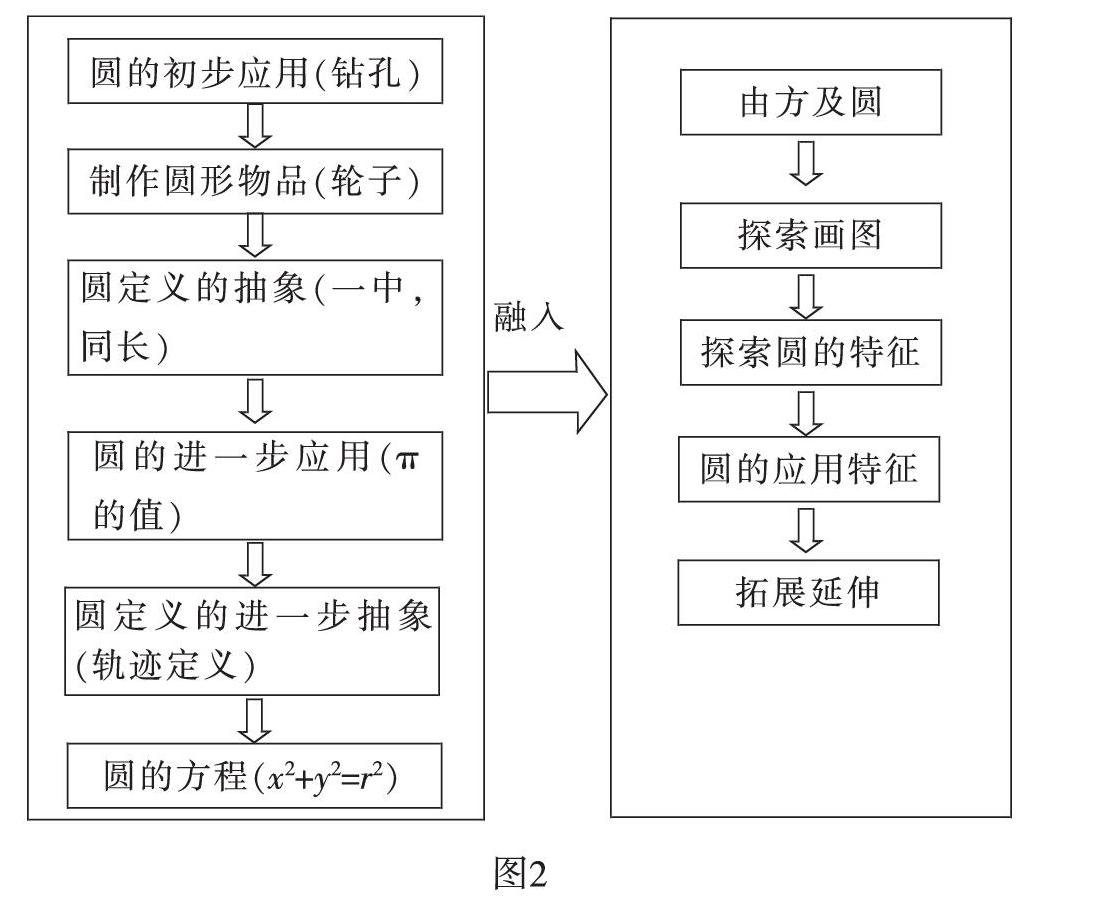
如何有效地设计,教师要关注三个方面:一是儿童的已有知识经验,如学习圆的认识,学生的已有知识是对由线段围成的平面图形的认识,经验是生活中观察到的圆形物体;二是要关注儿童的生活,要将数学知识镶嵌在学生熟悉的生活情境中;三是要关注数学知识的历史,情境的设计要围绕相关的数学史组成知识结构,使数学情境充盈着文化的积淀和历史脉络,为学生提供一种浸润式的数学学习场域。图2就是笔者在圆的认识的教学设计中的一种尝试。
(三)经历过程,感悟文化内涵
文化意义上的数学观以包容、多元和整体的视角重新审视学生的数学学习。上面提到数学文化要通过感悟获得,而要有感悟,就必须亲历过程,具体地说就是要经历再创造的过程。弗赖登塔尔曾说:“数学是系统化了的常识。”数学设计通过情境引入学习活动,让学生亲身经历将实际问题抽象成数学模型并进行解释和应用的过程。在这种深切关注学生生命体验的“再创造”过程中要注意三个方面的问题:一是正确对待差异,学生由于生活背景、知识经验及学习方式存在差异,他们对知识的探索、理解和领悟也会存在差异,教学中教师要用多元和宽容的眼光鼓励学生个性化地学习;二是及时把握动态,学生对知识的探索和感悟是一个动态的过程,教师的教学要根据学生的动态变化及时调整和改进;三是关注多元表征,数学学习过程中对数学文化的领悟往往只能意会而不能言传,这种理解和感悟往往可以通过不同的方式进行表征,肢体的、艺术的、言语的等,教师要关注每一个学生在数学学习中的各种反应。
二、“圆的认识”教学设计及思考
有关圆的知识历来都是小学数学教材中“图形与几何”领域非常重要的内容。从相关资料发现,对圆的认识,很多国家(包括我国)的数学课程标准都是这样安排的:一、二年级直观认识圆,三、四年级教学圆的特征,五、六年级教学圆的周长和面积。这是比较符合儿童的年龄特征和认知规律的。但如果從数学文化的层面,我们在教学“圆的认识”时应该有不同的意蕴。
(一)创设情境,初步感知
出示正方形花园,思考从哪一点走向四个角的距离相等?
操作:学生自己用正方形纸画一画。
出示正八边形,想想这样的路有几条?正十六边形呢?
想一想:这样一直下去会是一个什么图形,会有这样的多少条路。
学生交流,揭示课题:圆的认识。
(二)动手操作,探究画圆
我们已经能想象出这样一个图形了,你能把它画出来么?比比看谁画得最好。学生画完后全班进行交流,展示画得比较好的圆,并说说你是如何画的。
同学们刚才画了这样的图形,能保证从中心点到边上的距离都相等吗?
小组讨论:怎么画才能确保中心点到各顶点的距离相等?
用圆规画圆的同学介绍一次画法后,其他同学学着用圆规画一个圆。
设计意图:这样的设计不是简单地教学生用圆规画圆的技能,而是通过正多边形的边数无限增加,逐步逼近圆形,让学生思考如何确保中心点到顶点距离一直保持不变,这实际就是圆规画圆的本质。
(三)自主探究,合作交流
1.认识圆心、半径、直径
出示正方形和圆,小组讨论:比较它们的相同点和不同点。
相同点:都有一个中心点(圆的中心点为圆心),都是轴对称图形。
不同点:正方形是线段组成的,圆是曲线图形;正方形的中心到四个顶点距离相等,圆的圆心到边上的距离都相等;正方形有4条对称轴,圆有无数条对称轴。
圆心到圆周上的距离就是圆的半径r。
通过圆心,两端都在圆周上的线段叫直径d。
同一个圆,直径是半径的两倍d=2r。
2.做一做
学生在自己画的圆上分别画出一条半径和直径,并标上相应的字母。
通过画直径和半径,及时巩固了所学的知识。
(四)教学思考
根据以上教学,我们可以体会到,融入数学史的教学设计,有三个基本特征:一是更准确地把握数学知识的本质;二是教和学的过程实现了“再创造”;三是教学目标指向深层次理解。
当然,基于数学文化视域的数学教学与新课标提倡的教学方式是完全吻合的,从知识目标上说,数学文化可以帮助学生理解数学;从过程与方法目标上说,数学文化提供了丰富的问题解决方法,可以拓宽学生的思维;从情感、态度和价值观的目标上说,数学文化可以提高学生的学习兴趣,激发学生的学习动机,使数学变得更亲和、 更令人愉悦、更激动人心,揭示出数学作为人类文化活动的本质。
