平面图形面积公理及其单元教学内容的逻辑结构
2021-10-28刘加霞


刘加霞
北京教育学院初等教育学院院长,教育心理学博士,教授,教育部国培专家库成员;提出“把握数学本质是一切教学法的根”“实证研究学生是有效教学的根本”“培训实质是改变与创新”等观点,以及“CARE伙伴式”校本研修模式;在《课程·教材·教法》《中国教育学刊》《中小学管理》《人民教育》《小学数学教师》《小学教学》等期刊发表论文百余篇,著作有《小学数学有效教学》《小学数学有效学习评价》《小学数学课堂教学设计》等。
求平面图形面积的过程贯穿整个数学发展史,从古代数学到17世纪的微积分、现代的测度论,乃至今天的分形理论都与面积问题息息相关。解决面积问题源于田亩丈量、赋税分配、天文观测等现实需要,其中蕴含着重要的数学思想方法,是培养学生数学思维能力的重要载体。
平面图形的面积是小学数学中的基础内容,其教材内容选择和编排顺序与数学发展史存在不同。教材编排依据数学发展逻辑,还是小学生的认知基础与思维水平?抑或融合二者?本文将分析面积的本质及公理、面积公式之间的逻辑发展脉络以及学生的认知基础和不同思维水平,依此进一步解释教材的编写逻辑。
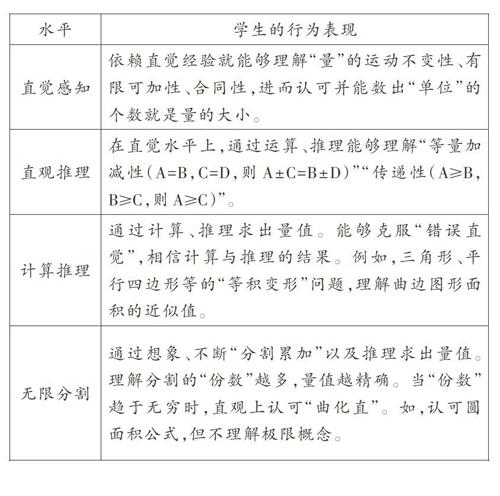
一、基于平面图形面积公理划分学生的认知水平
人对物体或图形的面积有与生俱来的直觉,早在婴儿阶段就已经能辨别两块饼的大小。比较面积大小与求出面积值是人的本能性活动。因此,学生无需花时间去理解面积的“描述性定义”,只要知道它是衡量区域大小的非负数值,即任何一个平面区域都与一个非负数建立“一一对应”关系,这个非负数就是面积单位的个數。因此,哪个图形的大小作为面积单位?是否让学生像学习长度一样经历“自创单位”到“标准单位”的过程?下述面积公理可以回答。
平面图形面积的存在是因为满足下述特性,可称之为面积公理(长度、体积、角度等都满足类似特性,这是测度论的基本性质)。
(1)正则性:规定边长为1的正方形,其面积为1。
(2)运动不变性:一个图形经过平移、旋转、反射等刚体变换后,其面积不变。
(3)合同性:完全重叠的两个图形其面积相等。
(4)有限可加性:整个图形的面积等于分割开的各部分图形面积之和。
小学生关于面积守恒性的不同理解水平是其理解面积概念、解决面积问题的前提,也是教材内容选择与编排的主要依据。根据面积公理及大量学生调研,笔者划分出以下四种水平。
无论是面积公理,还是学生的认知水平,都基于平面图形面积的本质,即覆盖住该图形的“小正方形(方格)”的个数。用“方格”作为面积单位是规定,如张奠宙所说“画方格、数方格是一切面积和体积问题的本质”,这是直觉水平的内容。如果再选其他“图形”,例如三角形、长方形甚至圆形等作为面积单位,反而显得“不自然”。教师设计用这些图形作为单位来度量不是有效、有价值的学习活动。我们学习长度单位经历“自创”(例如庹、拃、步等)到“国际标准”的过程,符合人的生活经验和历史发展,而面积单位的产生没有这个过程。
理解曲边图形面积的近似值需要学生的思维达到第三、第四种水平。小学生很难真正理解圆(曲边图形)的面积公式:“无限细分”使小方格的面积“趋于0”,全部小方格面积之和的极限是该图形的面积(用积分求面积时,面积微元不是“小正方形”,而是“小长方形”)。大多数小学高年级学生能够想象“由无限分割实现‘曲化直”,即只是认可圆面积公式,但不能真正理解极限概念。
现实中,解决图形面积问题很少用“数方格”的方法,因为不够简便,一般用面积公式计算,即计算两个“长度”的乘积。研究图形面积公式是中外数学中的重要内容。
二、数学史视角下各平面图形面积公式的推导与逻辑关系
古代各民族数学都研究面积问题,所用方法不尽相同:中国利用“以盈补虚法(出入相补)”,印度使用“面积拼补法”,希腊采用“面积贴合法”。前两者重在解决实际问题,认为“出入相补”“面积拼补”是不证自明的,后者重在推理证明。总体上看,中国古代几何一般不讨论图形离开数量关系的性质,重视计算出长度、面积、体积等,以解决现实问题,没有发展出基于公理的几何演绎体系。但也有数学家重视并给出平面图形面积公式的证明。
我国最早研究面积问题的著作《算数书》和《九章算术》,都以长方形(方田)面积公式为逻辑起点。例如《九章算术》“方田章”中的“方田术(以“步”为长度单位)、里田术(以“里”为长度单位)”、大广田术(长、宽是假分数)中给出长方形面积公式“广从(‘广指长方形的‘宽或‘东西方向线段长度,‘从指长方形的‘长或‘南北方向线段长度)步数相乘得积步、广从里数相乘得积里”,但都没有对此进行证明。“少广章”则给出该公式的实际运用:已知面积数、一边的长度(假分数),求另一边长。《九章算术》重视算法,给出了各种“术”,但没有证明过程,缺少演绎体系的构建。
刘徽在注述《九章算术》时也未证明长方形面积公式,只给出面积定义“凡广从相乘谓之幂”。唐初李淳风注述《九章算术》时有进一步证明,其推导过程与图1所示原理相同。这与当下教材中第一行摆“4个小正方形”,摆“这样的3行”不完全相同(图略)。
刘徽以长方形面积公式为逻辑起点证明其他平面图形面积公式。如运用“以盈补虚法”证明了圭田(等腰三角形)的“半广以乘正从”、邪田(直角梯形)与箕田(一般梯形)的“舌、踵和的一半乘正从”等面积公式。这与当下小学数学教材中的证明过程不同。
《九章算术》提出了圆面积的四种算法,第一种是“半周半径相乘得积步”。刘徽运用著名的“割圆术”——从圆内接正六边形出发,开始“割圆”,得到正[6·2n]边形序列,通过“割之弥细,所失弥少”的极限思想证明了圆面积公式。这个思想与古希腊阿基米德的方法异曲同工,只不过阿基米德研究的是圆的周长。郭书春教授认为,“割圆术”不仅仅是求圆周率的方法,更“证明”了圆面积公式的成立,蕴含着极限思想。祖冲之在“割圆术”基础上,得益于中国筹算的“位值制”(因为有“0”的地方就有“空格”,计算不会混淆),而使圆周率精确到小数点后第7位数字。这在世界上领先千年左右,但其思想性逊于“割圆术”。
三、教材内容选择和编排与数学发展史的异同
当下各版本教材内容选择和编排顺序与人们认识平面图形面积的发展过程基本一致,主要包括四个进程:用重叠法比较两个图形面积的大小;用“方格(单位)”测量某个图形,单位个数就是其面积;用公式计算平面图形面积;用微积分方法求曲边图形及曲面的面积。小学阶段主要学习前三个内容,第四阶段属于高等数学范畴,在小学只是略有渗透。
教材中各个平面图形面积公式的呈现顺序、推导方法与数学发展史存在不同,主要表现在以下几个方面。
1.长方形面积公式的推导过程与方法不尽相同
数学发展史上要么把长方形面积公式作为“公理”不加证明地使用,要么用“从而疏之,又横而截之”的分割方法说明;教材则采用“拼摆方格”的度量方法得出面积公式。
2.平行四边形面积公式的处理方式不同
中国古代数学中,长方形是所有图形面积公式推导的起点,然后是三角形、梯形、圆形及扇形等面积公式,没有明确提出平行四边形面积公式。1952年,由俞子夷主编、人民教育出版社出版的高级小学教材《算术课本》基本按照数学史的发展进程编排,没有编入平行四边形面积公式。20世纪60年代以来的小学数学教材都将平行四边形通过“割补”转化为长方形计算面积,然后再研究三角形、梯形的面积。
从数学学科发展角度看,不需要平行四边形公式。因为长方形与三角形面积公式是根本,其他所有平面图形都可以转化为这两个图形求面积、得出公式。从小学生知识基础、思维水平看,学生难以理解用出入相补法推导三角形、梯形面积公式,所以必须先学习平行四边形面积公式,再用“倍积法”将两个全等三角形、梯形转化为平行四边形得出面积公式。因为推导平行四边形面积公式所涉及的数学知识、“等积变形(面積守恒)”原理等,学生凭借直觉就可以接受,不需要补充其他数学概念、判定定理。
3.三角形、梯形面积公式的推导方法不同
当下教材中三角形、梯形面积公式的推导方法与刘徽的“出入相补法”不同。教材用“倍积法”(如图2)将三角形转化为平行四边形。有的教师教学时也补充转化为长方形的方法,如图3所示。
“倍积法”涉及的数学知识以及思维水平相对简单,而“出入相补法”是将一个三角形沿其高与中位线做“割补”,此方法需要做“辅助线”,要用到中位线、平行线的性质以及三角形全等的判定等知识,推理过程较复杂,不适合所有五年级学生。但对部分学生而言,出入相补法处于他们的最近发展区,更有挑战性和探究性。对五年级学生而言,“倍积法”没有知识难点但有思维难点。如果教师不提供两个全等三角形学具,学生能独立创造出“倍积法”吗?如果教师提供了学具,让学生通过操作、推导得出三角形面积公式,又容易沦为“为操作而操作”,使学生缺少数学思维的深度卷入。小学阶段用“倍积法”还是用出入相补法推导三角形、梯形面积公式,需要我们深入研究。
此外,南宋时期的秦九韶给出求三角形面积的方法——三斜求积术,即已知三角形三边求其面积的方法,用现代数学符号表示就是:
[S=14a2b2-(a2+b2-c22)2]
根号下多项式因式分解后所得到的三角形面积公式与古希腊海伦公式是等价的,小学阶段不学习该公式。
4.圆面积公式推导方法不同
各版本教材都没选用刘徽的“割圆术”推导圆面积公式。因为用内接正多边形面积与外切正多边形面积“夹逼”出圆的面积的方法,超出了小学生的知识基础和思维水平。教材采用将圆平均分成小扇形,再拼摆转化为平行四边形或长方形的方法。这是因为小学生难以理解极限思想,只能借助“想象”感受“无限分割”过程,认可“拼摆而成的平行四边形面积就是圆的面积”。
因此,小学数学教材内容的选择与编排,在遵循学科发展逻辑基础上,以学生的生活经验、知识基础以及思维水平为主要依据。这与数学史发展脉络不完全一致。
责任编辑 刘佳
