Breathers and solitons for the coupled nonlinear Schr¨odinger system in three-spine α-helical protein∗

Xiao-Min Wang(王晓敏) and Peng-Fei Li(李鹏飞)

1Department of Physics,Taiyuan Normal University,Jinzhong 030619,China

2Institute of Computational and Applied Physics,Taiyuan Normal University,Jinzhong 030619,China

Keywords: breather,soliton,nonlinear Schr¨odinger system,α-helical protein

1. Introduction

The nonlinear Schr¨odinger equation (NLS) is a wellknown nonlinear model in physics, optical fiber, fluid mechanics, biological science and Bose–Einstein condensates(BECs), which has aroused extensive research interest in recent decades. The discovery of soliton wave solutions for the NLS equations has stimulated researchers’ attention.[1–5]In the absence of optical losses, the propagation dynamics of soliton pulses are governed by NLS equation. At zero temperature,the dynamics of BEC are precisely described by the Gross–Pitaevskii equations which is similar to the NLS equation in nonlinear optics and plasma physics.[6,7]Due to the growing interest in the nonlinear phenomena, coupled NLS equations have attracted much attention,[8]which can be used to describe the interaction among the modes in the case of birefringent and other two-mode fibers.[9,10]This paper focuses on the application of coupled NLS equation in biological science,and studies it in the context of Davydov soliton inα-helical proteins.

Proteins are the kinds of important biological macromolecules existing in all organisms. Inα-helical proteins,the peptide sequence(H–N–C=O)forms the helical structure,which is stabilized by three quasi-linear hydrogen bonds between NH and CO groups in the main chain. In each peptide group, quantum transition occurs due to the vibrational structure of C=O double bond (amide-I) in the infrared region. Phonons will propagate from one group to another through the system, resulting in dispersion effect. Davydov applied Mcclare’s suggestion to theα-helical protein molecule to explain the conformational changes of muscle contraction caused by the energy, which supplied reaction to the adenosine-triphosphate (ATP) hydrolysis.[11,12]He believed that amide-I energy can be localized through the nonlinear interaction between vibration excitation and protein structure deformation due to excitation. The excitation and deformation offset each other and form solitons. Strictly speaking,solitons are localized exact solutions of integrable nonlinear partial differential equations with elastic collisions. By studying the energy dependent Hamiltonian,it is usually proposed to use the NLS equation to simulate the soliton,which was first proposed by Davydov.[11]The various properties of this unidimensional polaron-like self-trapped state are studied in discrete and continuous modes.[13–15]

Shortly after this discovery, many authors have studied the nonlinear excitation inα-helical chain.[16–20]However,in all of the above work,the dynamics of a single molecular chain was considered.Recently,considering the interspine coupling,the dynamics of a slightly modified Davydov model[21–26]on discrete and continuous levels is studied. It is found that the excitation is controlled by soliton mode. Actually,the dynamics of these soliton excitations are considered to be controlled by the coupled NLS equations. We need to regard to the nonhomogeneous nonlinearity so as to obtain the stable solution of three-spineα-helical protein,and the governing equation is the three-coupled NLS equation

where the variablesxandtrepresent the distance and time,respectively,ujrepresents the probability amplitude of thej-th spine, and the external uneven potentialV(x,t) comes from the impurity caused by the local thermal fluctuation effect and the disorder of the protein structure or the distortion of the virus infection.g(t)is a function oft,which is due to the imbalance of the parameters determined by the protein molecular structure and environmental conditions. In the ideal protein,the values of thet-related parameters are also considered to be a small fluctuation near the corresponding constant without any disorder.

The special cases of Eq. (1) have appeared in physical science and have been studied, such as the constant coefficient coupled NLS equation[27,28]and the generalized variable coefficient single NLS equation.[29–31]In addition,Qinet al.[32]studied a three-coupled NLS equation with external non-uniform potential as follows:

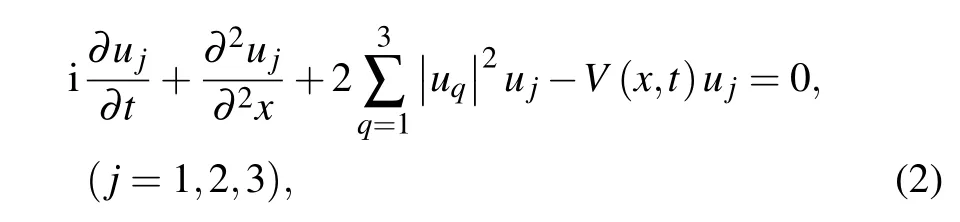
and the exact bright solutions and the shape-changing collision have been received. The bright solitons of Eq. (1) have been constructed by Konget al.,[29]and the dynamic behavior of solitons in the system with nonlinear coefficientg(t) as a periodic function ofthas been discussed. The bright and dark soliton dynamics have been discussed in Ref. [33] when the coefficient of Eq.(1)is in the form of hyperbolic secant function. However,it is poorly understood about the breather and its interaction inα-helical protein, and in fact, breathers and their collisions are very important in optics[34–36]and other systems.[37–39]Whether the breathers can be transformed into solitons has not been discussed. In this paper, breather-tosoliton conversions and the influence of the parameters on soliton distribution are studied in detail. The nonlinear wave interactions will also be analyzed.

The following is the rest of the paper. In Section 2,we construct the breather solutions of the three-coupled NLS equations.In Section 3,the breather-to-soliton conversions are constructed, several kinds of combined solitons are derived,and the characteristics of the interactions among breathers and solitons are analyzed. The influence of the parameters on soliton is also studied. Section 4 is the conclusion.

2. Exact breather solutions of the three-coupled NLS equations

In order to obtain the analytical solution of Eq. (1), the following form of similarity transformation is used:

We get a simple equation,which can be easily solved by Hirota bilinear method.

2.1. One-breather solution

By using the ansatz ofUj=Hj/F,following the steps of Hirota bilinear method, and substituting it into Eq. (4), oneand two-breather solutions of Eq.(4)can be obtained.

The one-breather solution reads

2.2. Two-breather solutions

The two-breathers solution reads

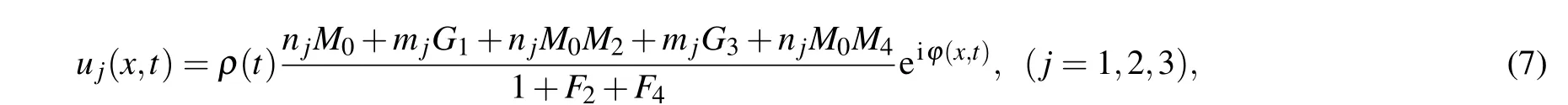
Fig.1. EvolutionofthebreathersolutionofEq.(5).Th√eparametersarechosen as k1=0.8+0.01i,γ0=1,α=5,k0=1,ρ0=1/3,g(t)=1,m1=1,n1=1,m2=1,n2=2,m3=1,and n3=−3.

Hereα1,α2,k1,k2,Ai j(i,j=1,2),κ1,µ12andµ21are all arbitrary complex parameters, whileµ11,µ22andκ2are real ones. Equation (7) is the two-breather solutions of Eq. (1).It means that two breathers are excited in the same spine for theα-helical protein. In protein molecules, energy is transferred by soliton motion. Soliton is named because the shape keeps unchanged during collision. The soliton collision happens possibly in organism, which is a basic problem in the study of protein molecular energy transfer due to it is related to whether energy can be transferred normally. The collision properties will be studied in the following section in detail.

3. Dynamic behavior of breathers and solitons and discussion

In this section, we consider an interesting example in physics,that is,the form of periodic time-varying nonlinearityg(t)=1+εsinωt,and one of the typical types of one-breather Eq.(5)and two-breather Eq.(7)is used to illustrate their dynamic behavior. And the breathers can be converted into solitons. Then we also study the effects of different parameters on the breathers and solitons dynamics.

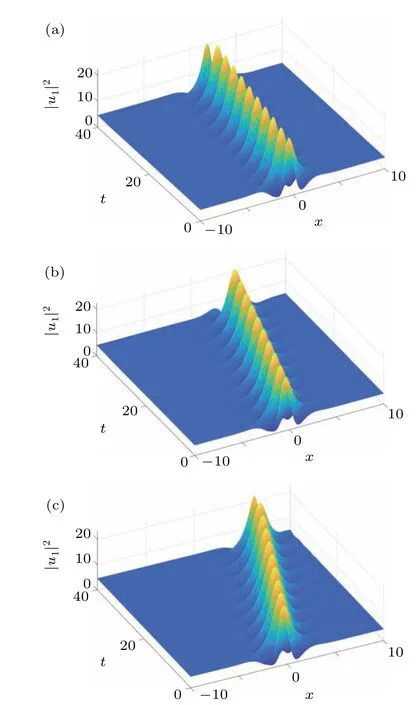
Fig.2. Evolution of the breather solution of Eq.(5). The parameters are chosen as those in Fig. 1 except (a) k1 =0.8+0.05i; (b) k1 =0.8+0.09i; (c)k1=0.8+0.13i.

3.1. The breathers and solitons on plane-wave background

Fig.3.Many types of combined solitons.The parameters are chosen as those in Fig.1 except(a)n2=0,n3=−1;(b)m2=0,n2=1,n3=−1;(c)n1=0,m2 =0, n2 =1, m3 =0, n3 =1.1; (d) n1 =0, m2 =0, n2 =1, m3 =1.1,n3=0.

We now study the wave evolution ofg(t)=1+εsinωtwithε=0, i.e.,g(t) is a constant. Solutions (5) characterizes the nonlinear waves with the breathing behavior on the plane-wave background. Figure 1 shows the dynamic behavior of three different chains in theα-helical protein. Sinceuj(j=1,2,3)changes in the same way,we only discuss the change ofu1for the sake of simplicity.As shown in the Fig.1,one can observe that the soliton of three chains in protein exhibits obvious periodic breathing behavior, and the peak and trough propagate slantingly in each circle. From Fig. 1(a),those breathers are periodic in thet-axis and aperiodic in thex-axis,that is to say,these are Ma-breather solitons can be observed. Compared with Fig.1(a),we adjust thek1I,the direction of soliton propagation has changed as shown Fig.2. The suffixes I denote the imaginary part ofk1. As time goes by,the center of the solitons moves to the positivex-axis. The larger thek1Iis,the larger the deviation between thexcoordinate of the soliton center and the linex=0 is.

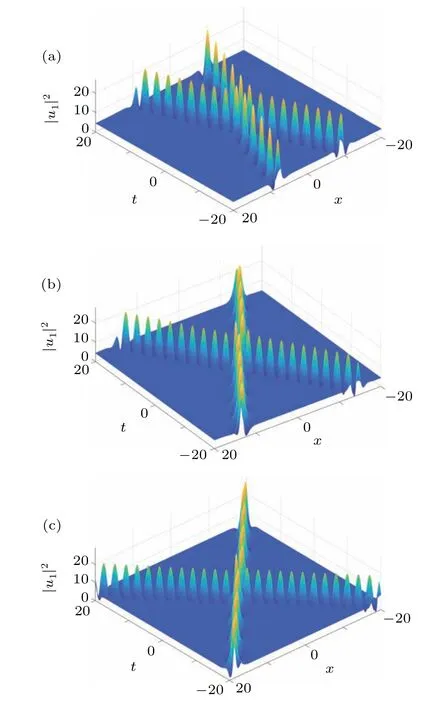
Fig.4. Evolution of the two-breather solutions of solution(7). The parameters are chosen as those in Fig.1 except α1=5,α2=5,and(a)k1=1+0.3i,k2=1−0.3i;(b)k1=1+0.5i,k2=1−0.5i;(c)k1=1+0.7i,k2=1−0.7i.

In Fig. 3, we present several types of vector solitons by choosing different forms ofmjandnj(j=1,2,3).Figure 3(a)shows 2-breather-1-bright solitons, i.e., the breathers are excited in the two hydrogen chains and the other hydrogen chain is excited bright soliton. Here,we only show that the first and the second chain are excited breathers,while the third chain is excited bright soliton. Figures 3(b)–3(d)show the 2-breather-1-dark,2-dark-1-bright and 2-bright-1-dark solitons by adjusting the values ofmjandnj. From Fig.3,we find many types of combined solitons are obtained. In other words, breatherto-soliton conversation transition can be achieved whenmjandnjtake special values. This provides a good theoretical support for soliton control. The influence of parametersk1andk2on the evolution of the two breathers,and the two solitons also have breather behavior closing to each other and then divided again after collision as shown in Fig.4. The sum of the amplitudes of the two breathers remains unchanged. It shows that there is no energy loss during the collision. Moreover,the effect of parametersk1andk2on the propagation direction of two solitons is the same as that of one soliton. The larger the absolute value ofk1Iandk2I,the larger the deviation between the center of soliton and the linex=0.

Fig. 5. Evolution of the breather on the periodic-wave background. The parameters are chosen as those in Fig.1 except g(t)=1+0.2sint.

From Figs. 1–4 we can see the breathers and solitons propagate on the plane-wave background wheng(t)is a constant. In the homogeneous case,the trajectory of the breather is in a straight line shape, as shown in Figs. 1 and 2. The breather velocity depends onk1I. By adjustingk1I, the direction of propagation can be changed. Two co-propagating breathers interact and share energy in the same spine and the collision is elastic, as shown in Fig. 4. Therefore, when the solitons propagate along the hydrogen bond spines, they will collide with each other,and their energy distribution in the adjacent spines will not change during the collision process,thus maintaining the total energy conservation.

Fig.6. Evolution of the breather on the periodic-wave background. The parameters are chosen as those in Fig. 1 except (a) g(t)=1+0.2sin2t; (b)g(t)=1+0.2sin4t;(c)g(t)=1+0.2sin6t.

3.2. The breathers and solitons on period-wave background

Fig.7. Evolution of the bright soliton. The parameters are chosen as those in Fig.1 except g(t)=1+0.2sint,m1=2,n1=0,n2=1,and n3=−1.

The intensity plots of bright-breather-breather is respectively as shown in Fig.7(a). The propagation dynamics of breather soliton are same in Fig. 5, and we only show the 1D image here. While the intensity of the bright soliton periodic oscillates due to theg(t) effect, and propagation path is also periodic as shown in Fig. 7(b). And it is found that the maximum amplitude of|u1|2increases with the increase ofα1.Whenα1are different from each other, the amplitudes of solitons are different too. This discrepancy may be due to the difference between the environment and the structure of each chain inα-helical protein. In the same way, we can get the breather-bright-breather and breather-breather-bright combined solitons whenn2=0 andn3=0,respectively.

Fig.8. Evolution of the dark soliton on the periodic-wave background. The parameters are chosen as those in Fig.1 except g(t)=1+0.2sinπt,m1=0,n1=2,n2=1,and n3=−1.

Asmj=0 (j=1,2,3), there are two-breather-one-dark solitons. Here we takem1=0 as an example, as shown in Fig.8(a). And Eq.(5)is simplified

wherel=2,3. Here, the dark soliton is excited in the first molecular chain,and the dark soliton is embedded the periodwave background as shown Fig.8(b). The dark soliton propagates in a period is shown in Fig. 9(c). At the same time,the other two kinds of combined solitons can also be obtained including 2-bright-1-dark and 1-bright-2-dark solitons.Their propagation dynamics are the same as those described in Figs.7(b)and 8(b),which will not be described here. In other words,due to the effect ofg(t),we can get the bright solitons with periodic oscillation and the dark solitons propagating in the periodic wave background from the breathers.

Fig. 9. Evolution of the two-breather solutions of solution (7). The parameters are chosen as those in Fig. 1 except k1 =0.4+0.7i, k2 =1 −0.7i,α1 =5, α2 =5, g(t)=1+0.2sint, and (a) n2 =1, n3 =−2; (b) n1 =0,n2=1,n3=−1;(c)m1=0,n2=1,n3=−1.

In Fig. 9, different types of two solitons are obtained by choosing different values ofmjandnj. Figure 9(a)shows the two breather solitons, and Figs. 9(b) and 9(c) are two bright and dark solitons, respectively. The standard elastic collision propagate only along with a center shift for the three types of solitons.

It can be seen from Figs. 5–9 that wheng(t) is a periodic function, the breathers and solitons propagate on the periodic wave background.g(t) is caused by the parameters imbalance determined by the protein molecular structure and environmental conditions. Periodic inhomogeneity arising due to periodic repetition at different locations or simple defects along the helical chain is incorporated in the form ofg(t)=1+εsinωt. The fluctuation in the local region is periodic in nature, which also leads to a disorder in the smooth functioning of the protein molecular systems. In this case,the energy can be transferred with good efficiency in theα-helical protein.

4. Conclusion

Our main attention has been focused on system(1)which describes soliton dynamics in the three-spineα-helical protein with inhomogeneous effect. The breathers and solitons on plane-wave and period-wave background for this system have been investigated. Many types of combined solitons including 2-breather-1-bright,2-breather-1-dark,2-bright-1dark and 2-dark-1-bright solitons have been constructed by adjusting parameters. We also have been discussed the propagation properties of those solitons under the influences related parameters have been discussed.