屈服准则和硬化模型对DC56D+Z钢汽车后背门内板成形仿真精度的影响
2021-10-28鄂宏伟李亚东郑学斌韩龙帅
鄂宏伟,李亚东,郑学斌,韩龙帅
(首钢集团有限公司技术研究院,北京 100043)
0 引 言
目前,计算机技术和有限元理论迅猛发展,金属板料成形仿真技术也得到广泛应用。仿真技术已成为汽车产品设计及生产过程中必不可少的辅助工具,能够大幅度缩短产品及模具的开发周期,降低研发成本[1]。金属板料成形仿真是汽车车身总体设计和部分零部件模具开发制造的关键,仿真结果的准确度对于整车设计和模具整改具有重要的指导意义。仿真结果的准确性与材料模型的选取密切相关,所述材料模型主要包括硬化模型、屈服准则等[2]。
近年来,学者们相继提出了各种硬化模型和屈服准则来描述材料的力学行为。常用的硬化模型包括Ludwik、Swift、Hockett-Sherby和Voce等[3-4];常用的屈服准则包括适用于各向同性材料的Tresca屈服准则和Mises屈服准则[5]。但大多数板料具有显著的各向异性[6],为此学者们提出了多种各向异性屈服准则,其中Hill系列屈服准则、Barlat系列屈服准则和BBC系列屈服准则都是较常见的模型,且都内嵌于大多数商业有限元软件中。Autoform软件中就内含典型的Hill′48[7]、Barlat′89[8]和BBC-2005屈服准则[9]。不同类别的硬化模型和屈服准则对于材料的适用性不尽相同,针对特定牌号的材料选择精确的材料模型,是提高其力学行为仿真精度的关键。作者基于Ludwik、Swift、Hockett-Sherby等3种硬化模型,对在汽车车身上应用最多的DC56D+Z超深冲钢进行材料性能参数解析,以确定能准确描述该钢流变行为的硬化模型;基于此,结合Hill′48、Barlat′89和BBC-2005屈服准则对DC56D+Z超深冲钢汽车后背门内板进行冲压成形仿真,研究不同屈服准则的适用性,为企业在生产中选择合适的材料模型提供参考。
1 常用硬化模型和屈服准则介绍
1.1 硬化模型
Autoform有限元分析软件[10]广泛应用于汽车行业中大型车身覆盖件的冲压成形仿真,其内含常用于描述钢材力学行为的硬化模型,包括Ludwik、Swift、Hockett-Sherby等。
Ludwik硬化模型的表达式为

(1)
式中:σ为流动应力;εp为塑性应变;k为材料参数;n为硬化指数。
Swift硬化模型的表达式为
σ=c(ε0+εp)m
(2)
式中:ε0为初始屈服应变;c,m为材料参数。
Hockett-Sherby硬化模型通过拟合流动应力-应变曲线而得到,表达式为

(3)
式中:σsat为拟合硬化曲线的屈服极限;σi为初始流动应力;a,b为材料参数。
1.2 各向异性屈服准则
1.2.1 Hill′48屈服准则
1948年,HILL[7]首次将材料各向异性参数引入到屈服准则中,提出了正交各向异性材料的屈服准则Hill′48,为板料塑性变形各向异性理论的建立奠定了基础。Hill′48屈服准则的函数表达式为

(4)

若满足3F=3G=3H=M=N,则Hill′48屈服准则转化为表征各向同性的Mises屈服准则。通常情况下,板料在成形过程中大多处于平面应力状态,即σzz,σyz,σzx均为0,则式(4)简化为
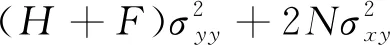
(5)
Hill′48屈服准则充分考虑材料的各向异性且囊括剪切应力元素,适用于二维和三维问题,其函数形式简单,参数求解便捷。因此,在保证精度的前提下,Hill′48屈服准则被广泛应用于解决实际工程问题,许多有限元软件都包含该准则[5]。
1.2.2 Barlat′89屈服准则
1989年,BARLAT等[8]为了更好地研究板料的各向异性,提出了各向异性屈服准则Barlat′89。Barlat′89屈服准则建立在平面应力条件下,该准则函数表达式为
a1|K1+K2|m1+a1|K1-K2|m1+

(6)

(7)
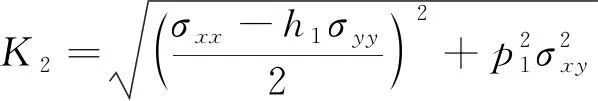
(8)
式中:a1,h1,c1,p1为相互独立的参数;m1为非二次屈服函数的指数。
对于面心立方材料,m1=8;对于体心立方材料,m1=6;而当m1=2时,Barlat′89屈服准则转化为Hill′48屈服准则。
1.2.3 BBC-2005屈服准则
综上所述,金属矿山矿下生产作业的核心实质是稳固安全。而电气自动化控制技术能有效地解决相关的安全问题。通过对矿下排水系统、通风系统与运输机械设备的远程自动化控制,可以有效预防与缓解矿下危险事故的发生,为其提高矿业产量与企业壮大发展打下坚持的保障基础
BANABIC等[9]在上述屈服准则的基础上提出了一系列BBC屈服准则,其中较为典型的是BBC-2005屈服准则,该准则具有更大的柔性,适用于钢、铝等材料的塑性成形;Autoform有限元软件也包含该准则。BBC-2005屈服准则的数学表达式为
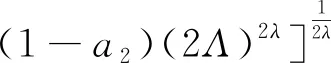
(9)
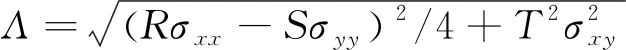
(10)
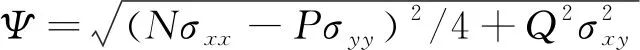
(11)
Γ=(σxx+Mσyy)/2
(12)
式中:λ为可调数,可根据材料的实际情况进行调节;Λ,Γ,Ψ是应力张量平面应力分量的函数;a2,R,S,T,N,P,Q,M为屈服准则中包含的8个各向异性系数,可由材料3个单向拉伸状态下的应力值(σ0,σ45,σ90)和塑性应变比值(r0,r45,r90),以及等双拉状态下的应力σb和塑性应变比rb通过数值计算的方法获得,下标0,45,90代表与轧制方向成0°,45°,90°角。
2 试样制备与试验方法
试验材料采用首钢生产的厚度规格0.65 mm的冷轧DC56D+Z超深冲钢。根据GB/T 228-2002,在试验钢板上分别沿轧制方向(0°方向)、与轧制方向成45°角(45°方向)和垂直轧制方向(90°方向)取标距为80 mm的“哑铃型”试样,采用Zwick-Z100型试验机进行准静态拉伸试验,拉伸应变速率为0.001 s-1,共完成9次平行试验。
3 不同硬化模型的精度对比
根据材料力学性能检测结果获取材料的力学性能参数,如表1所示,表中:Rp0.2为屈服强度;Rm为抗拉强度;n为硬化指数;r为塑性应变比。将试验获取的工程应力-应变曲线换算为如图1所示的真应力-真实塑性应变曲线,转算公式如下

图1 DC56D+Z钢0°方向的真应力-真实塑性应变曲线Fig.1 True stress-true plastic strain curve of DC56D+Zsteel in 0° direction
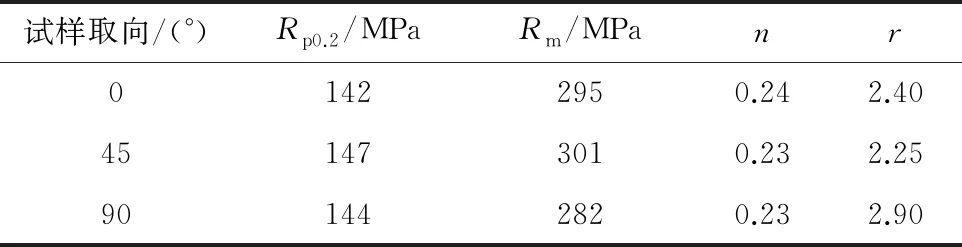
表1 DC56D+Z钢的力学性能参数
εT=ln(1+εnom)
(13)
σT=σnom(1+εT)
(14)
εp,T=εT-σT/E
(15)
式中:εnom为工程应变;σnom为工程应力;εT为真应变;σT为真应力;εp,T为真实塑性应变;E为弹性模量,取210 MPa。
基于MATLAB软件,分别采用Ludwik、Swift和Hockett-Sherby硬化模型对DC56D+Z钢0°方向的真应力-真实塑性应变曲线进行拟合计算,各硬化模型的参数和计算精度如表2所示,拟合得到的真应力-真实塑性应变曲线与试验曲线的对比见图2。由表2和图2可以看出,Hockett-Sherby硬化模型对于DC56D+Z钢的力学行为具有更高的描述精度,拟合相关系数的平方R2为0.997 9。因此,后文将基于Hockett-Sherby硬化模型并结合复杂车身覆盖件变形过程的应力、应变情况,对比Hill′48、Barlat′89和BBC-2005屈服准则的适用性。

图2 不同硬化模型计算得到真应力-真实塑性应变曲线与试验曲线的对比Fig.2 Comparison of true stress-true plastic strain curvescalculated by different hardening models with test curve
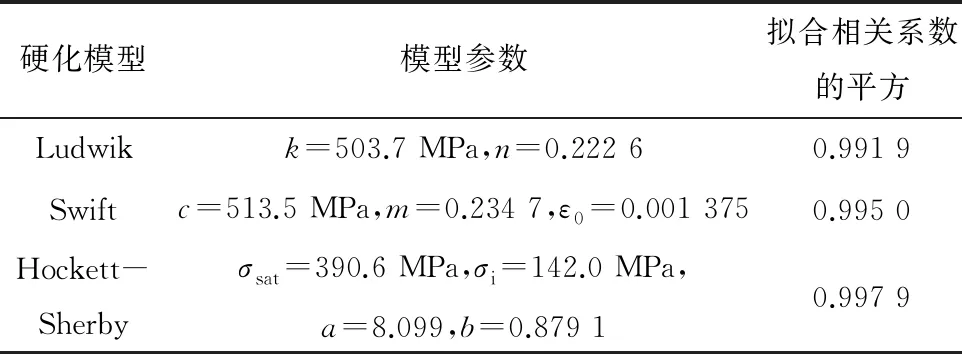
表2 不同硬化模型的参数及计算精度
4 基于不同屈服准则的后背门内板成形有限元仿真及结果
4.1 后背门内板成形有限元仿真
基于Autoform有限元软件对某车型后背门内板成形进行仿真,该后背门内板实物见图3(a)。以DC56D+Z超深冲钢制后背门内板拉延序产品为研究对象,通过Autoform有限元软件建立的后背门内板拉延序仿真模型如图3(b)所示,拉延序产品有限元模型如图3(c)所示,材料性能详见表1。有限元仿真网格单元类型设置为EPS-11,网格数为8 845个,拉延工艺参数设置与产品实际生产参数保持一致。应用Hill′48、Barlat′89和BBC-2005等3种屈服准则,对拉延成形过程进行仿真,分析材料流动状态、应变分布和减薄率,并与试验结果进行对比。

图3 汽车后背门内板实物图、拉延序仿真模型和拉延序产品有限元模型Fig.3 Physical image, drawing sequence simulation model and drawing sequence product finite element model of automobile rear door inner panel
4.2 屈服准则的适用性对比
4.2.1 材料流动量
后背门内板为对称件,因此在其一侧变形量较大区域选取5个特征点作为研究对象,取点位置如图3(c)所示。其中,点1和点2反映的是平行于轧制方向的材料流动状态,点3和点4反映的是圆角处材料流动状态,点5反映的是垂直于轧制方向的材料流动状态。通过Autoform有限元软件基于不同屈服准则模拟得到后背门内板成形后材料流动量云图,如图4所示。由有限元软件的结果后处理窗口提取不同屈服准则下的各点材料流动量,也列于图4中。试验测得对应点1,2,3,4,5处的材料流动量分别为44.84,34.87,33.91,33.58,71.82 mm,仿真结果与试验结果的相对误差见图5。
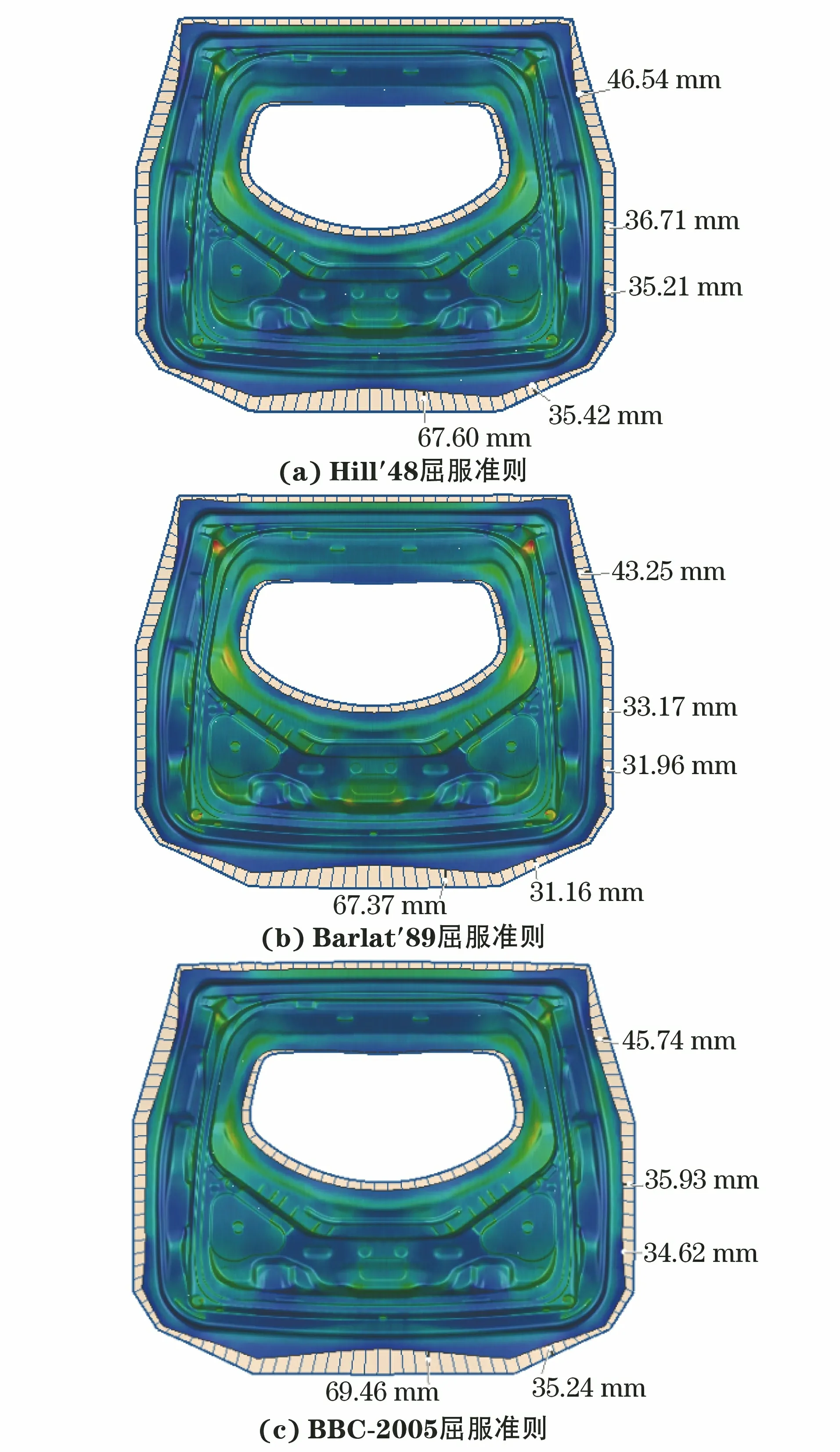
图4 基于不同屈服准则仿真得到冲压成形汽车后背门内板的材料流动量云图Fig.4 Material inflow nephogram of stamping automobile rear door inner panel by simulation with different yield criteria: (a) Hill′48 yield criterion; (b) Barlat′89 yield criterion and (c) BBC-2005 yield criterion

图5 基于不同屈服准则仿真得到材料流动量与试验结果的相对误差Fig.5 Relative errors of material inflow simulated by differentyield criteria and test results
由图5可以看出,BBC-2005屈服准则对材料流动量的预测精度最高,仿真得到的材料流动量与试验结果的最大相对误差在4.9%。这是因为该屈服准则同时考虑了材料的应力以及变形各向异性参量,对材料流动量的预测更符合实际情况。
4.2.2 最大主应变及厚度减薄率
基于3种屈服准则仿真得到的后背门内板应变云图以及利用Argus应变测量系统获取的应变云图如图6和图7所示。在图6和图7中对应的A,B,C区域提取最大主应变和厚度减薄率,结果分别见表3和表4,相对误差见图8。

图7 试验获取冲压成形汽车后背门内板的网格应变分布Fig.7 Mesh strain distribution of stamping automobile rear door inner panel by tests: (a) whole; (b) area A; (c) area B and (d) area C

表4 不同屈服准则下仿真得到后背门内板不同区域最大减薄率与试验结果

图6 基于不同屈服准则仿真得到冲压成形汽车后背门内板的应变云图Fig.6 Strain cloud diagram of stamping automobile rear door inner panel by simulation with different yield criteria: (a) Hill′48 yield criterion; (b) Barlat′89 yield criterion and (c) BBC-2005 yield criterion

表3 不同屈服准则下仿真得到后背门内板不同区域最大主应变与试验结果
由图8可以看出,BBC-2005屈服准则对最大主应变和最大减薄率的预测精度都优于Hill′48和Barlat′89屈服准则,采用BBC-2005屈服准则预测得到的最大主应变和最大减薄率与试验结果的最大相对误差分别为5.6%,10.1%。Hill′48和Barlat′89屈服准则对于材料厚度减薄率的预测精度相差不大,但Hill′48屈服准则参数求解简便,在仿真精度允许的情况下也可选用该屈服准则对材料减薄率进行分析。综上所述,BBC-2005屈服准则同时纳入材料的应力和变形各向异性等参数,能更全面描述材料的力学行为,更适用于DC56D+Z超深冲钢板的成形仿真和缺陷预测。
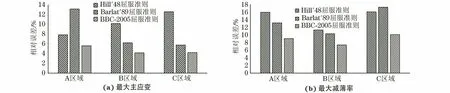
图8 不同屈服准则下仿真得到最大主应变和最大减薄率与试验结果的相对误差Fig.8 Relative errors between maximum principal strain (a) and maximum thinning rate (b) simulated with different yield criteria and test results
5 结 论
(1) 基于Ludwik、Swift和Hockett-Sherby等3种硬化模型对DC56D+Z超深冲钢进行材料性能参数解析,其中Hockett-Sherby硬化模型对该钢真应力-真实塑性应变曲线具有更高的描述精度,拟合相关系数的平方为0.997 9。
(2) 基于Hockett-Sherby硬化模型并分别搭载Hill′48、Barlat′89和BBC-2005屈服准则对某车型后背门内板进行冲压仿真,其中BBC-2005屈服准则同时考虑应力以及变形各向异性等参数,对材料流动状态、最大主应变和最大减薄率等参数的仿真精度都明显高于Hill′48和Barlat′89屈服准则,对材料流动量、最大主应变和最大减薄率的仿真结果与试验结果的最大相对误差分别为4.9%,5.6%,10.1%,说明BBC-2005屈服准则在DC56D+Z超深冲钢的冲压成形结果预测中更为适用。
