基于J-C模型的GH907高温合金动态本构关系及失效关系

董泽民，陈 伟，刘璐璐，徐凯龙，赵振华

(南京航空航天大学1.能源与动力学院，航空发动机热环境与热结构工业和信息化部重点实验室，2.机械结构力学及控制国家重点实验室，南京 210016)

0 引 言

GH907高温合金是一种以铁-镍-钴为基的低膨胀高温合金，在650 ℃以下具有很高的强度、低的膨胀系数、良好的热疲劳性能以及几乎恒定不变的弹性模量，因而在制造航空发动机机匣、隔热环等环形件上应用广泛[1]。航空发动机在运行过程中，其机匣容易受到叶片故障产生的高动能碎片的冲击，给飞行安全带来隐患。而在研制阶段，发动机机匣包容试验成本高，耗时长，因此数值模拟成为非常重要的研究方法。准确描述机匣材料在高温、高应变速率下的动态本构关系以及损伤失效关系对于航空发动机机匣的包容数值模拟至关重要。目前，在众多常用的描述金属材料的动态本构模型及失效模型中，Johnson-Cook(J-C)模型[2-3]因形式简洁、物理意义明确并且可以通过分离变量的方式标定参数而被学者们广泛采用。

国内外学者已经对航空发动机常用高温合金的动态力学性能进行了广泛的研究。刘晓等[4]对GH4169合金进行了J-C本构模型和失效模型的拟合，对本构模型中的对数应变速率项系数进行了线性修正，并通过动态压缩试验和仿真验证了模型的有效性。LIU等[5]采用2套不同参数的J-C模型描述了不同温度范围GH4169合金的本构关系，并通过数值仿真模拟了弹丸冲击靶板过程，结果表明仿真预测的弹道极限及失效模式与试验结果具有较好的一致性。KORKMAZ等[6]通过对Nimonic 80A高温合金进行不同温度、不同应变速率的拉伸试验获取了J-C模型参数，并通过数值仿真模拟动态拉伸试验验证了参数的准确性。HAQ等[7]采用J-C模型描述Inconel-718合金靶板的本构和失效行为，利用数值仿真方法探究了不同顶角的圆锥形弹体对靶板破坏模式和弹道极限的影响。WANG等[8]提出修正的J-C本构模型和失效模型来表征发动机包容环常用GH3536高温合金的动态力学行为，并利用数值仿真对该材料蜂窝结构在不同温度、冲击速度和冲击角度下的抗冲击性能进行了分析，结果表明修正的模型比原始J-C模型具有更准确的表征能力。UGODILINWA等[9]研究了新型航空高温合金Haynes 282在3种不同热处理条件下的准静态和高应变速率压缩变形行为，建立了Arrhenius和改进的J-C本构模型来描述材料在高应变速率和高温下的动态力学行为。BORA等[10]和WANG等[11]分别在J-C失效模型中引入不同表达式的Lode应变参数来表征材料的动态失效行为。

目前，有关GH907合金的研究主要集中在表面涂层的抗氧化性能[12]、耐腐蚀性能[13]、热处理工艺和显微组织[14]等方面，关于该合金在不同温度、不同应变速率下的动态力学行为研究并不多见。丰建朋等[15]在分析3种Arrhenius型方程的基础上，以Zener-Hollomon参数为主要变量，并综合考虑应变、应变速率和温度的影响，建立了GH907合金在应变速率10-2～10 s-1范围内的本构关系；但是该应变速率范围较小，且未考虑失效模型的影响。作者以GH907合金为研究对象，使用材料试验机在常温下进行光滑圆棒和缺口试样的准静态拉伸试验，并使用分离式霍普金森拉杆试验装置进行了应变速率在1 000～3 000 s-1的动态拉伸试验，还使用分离式霍普金森压杆(SHPB)试验装置进行了温度在20～400 ℃、应变速率在600～3 000 s-1的动态压缩试验，获得了用于描述GH907合金在较宽温度和应变速率范围内的力学性能的J-C模型参数，并通过SHPB仿真验证本构模型参数的有效性，拟为打靶和机匣包容数值模拟提供依据。

1 试验材料与方法

试验材料为GH907高温合金，其化学成分[1]如表1所示。

表1 GH907高温合金的化学成分

在100KN电子万能材料试验机上进行室温和高温准静态拉伸试验。室温准静态拉伸用光滑圆棒试样和缺口试样的形状和尺寸分别见图1(a)和图1(b)，为了获得较宽应力三轴度范围内合金的力学性能，设计了4种缺口尺寸，缺口半径R分别为1.0，1.5，3.0，6.0 mm。通过速率控制的方式加载，光滑试样的名义加载应变速率分别为0.000 1，0.001，0.01 s-1，缺口试样的名义加载应变速率为0.001 s-1。高温准静态拉伸用光滑圆棒试样的形状和尺寸见图1(c)，通过管式加热炉对试样及其转接段加热，外置程序控制炉温及保温时间，温度分别为80，160，240，320 ℃，保温时间为1 h，应变速率为10-3s-1。利用直径20 mm的分离式霍普金森拉杆试验装置进行室温动态拉伸试验，动态拉伸试样的形状和尺寸见图1(d)，夹持端与拉杆进行连接，并通过应变片、示波器等装置采集试验中的波形信号，试验时的应变速率分别为1 700 s-1，2 100 s-1，2 700 s-1。通过压杆直径14.5 mm的SHPB试验装置进行室温(20 ℃)和高温动态压缩试验，撞击杆长0.4 m，动态压缩试样的形状和尺寸如图1(e)所示。高温动态压缩试验中试样的温度通过热电偶测定加热炉炉膛中心温度代替，试验温度分别为200，400 ℃，通过应变片、动态应变仪等装置采集试验中的波形信号，应变速率分别为600 s-1，1 000 s-1，1 400 s-1，1 700 s-1，1 800 s-1，2 000 s-1。

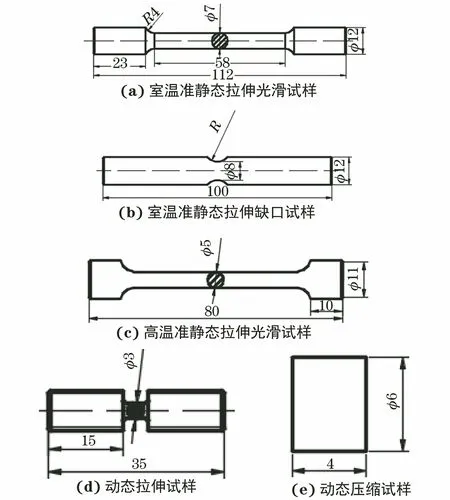
图1 试样的形状和尺寸Fig.1 Geometry and dimensions of specimens: (a) room temperature quasi-static tension smooth specimen; (b) room temperature notched quasi-static tension specimen; (c) high temperature quasi-static tension smooth specimen; (d) dynamic tension specimen and (e) dynamic compression specimen

2 试验结果与讨论

2.1 拉伸性能

由图2可以看出，GH907合金具有明显的屈服平台，是一种典型的韧性金属材料。在准静态拉伸试验中，尽管应变速率不同，但试验结果仍具有较好的重复性。

图2 光滑试样的准静态拉伸真应力-真应变曲线Fig.2 True stress-true strain curves of smooth specimens during quasi-static tension

由图3可以看出：随着缺口半径的增大，缺口试样发生破坏时的载荷整体上呈现出减小的趋势，并且发生破坏时的位移几乎相同，远小于光滑圆棒试样破坏时对应的位移。这是因为对于GH907合金这种塑性材料来说，缺口带来的三向应力状态以及应力集中现象，约束了材料内部的塑性变形。缺口试样的屈服强度和抗拉强度都比光滑试样明显提高，同时达到破坏时的变形量也更小，脆性有所增强。

图3 光滑试样和不同尺寸缺口试样的准静态拉伸载荷-位移曲线(应变速率0.001 s-1)Fig.3 Load-displacement curves of smooth and different-notch-sized specimens during quasi-static tension (0.001 s-1 strain rate)

由图4可以看出，在变形温度80～320 ℃范围内，GH907合金准静态拉伸载荷-位移曲线弹性段的斜率基本一致，进入强化段呈现出明显的软化趋势，且随着温度的升高，合金达到峰值载荷所需位移有所增大。

图4 不同温度下光滑试样的准静态拉伸载荷-位移曲线(应变速率0.001 s-1)Fig.4 Load-displacement curves of smooth specimens during quasi-static tension at different temperatures (0.001 s-1 strain rate)

由图5可以看出，在较高应变速率(1 7002 700 s-1)的条件下，GH907合金没有明显的屈服段，同时屈服应力和流动应力都表现出明显的应变速率强化效应，高应变速率下达到抗拉强度的应变远小于准静态条件下的。

图5 常温下光滑试样的准静态和动态拉伸真应力-真应变曲线Fig.5 True stress-true strain curves of smooth specimens during quasi-static tension and dynamic tension at room temperature

2.2 压缩性能

由图6可以看出，GH907合金具有明显的应变硬化效应，但是不同加载应变速率下，硬化曲线几乎平行，表明合金在压缩应变速率600～2 000 s-1范围内没有明显的应变速率强化效应。这归因于在高的加载速率下，材料内部的热量来不及散发引起的热软化效应与应变速率强化效应的相互抵消。

图6 常温下试样的动态压缩真应力-真应变曲线Fig.6 True stress-true strain curves of specimens during dynamic compression at room temperature

由图7可以看出，随温度从室温升到400 ℃，GH907合金硬化阶段的整体真应力-真应变曲线有明显的下移趋势，表现出了材料的温度软化效应，同时卸载应变也随着温度的升高呈现下降趋势。

图7 不同温度下试样的动态压缩真应力-真应变曲线Fig.7 True stress-true strain curves of specimens during dynamic compression at different temperatures

3 本构、失效模型的建立及验证

3.1 本构模型的建立

J-C本构模型[2]的表达式为

(1)

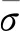
式(1)右侧3项依次表征材料的硬化效应、应变速率效应及温度效应。参数A，B，n可以通过室温下光滑圆棒试样的准静态拉伸试验获得。在参考应变速率和室温下，式(1)的后2项均等于1，则式(1)可改写为

(2)

参数A的值等于材料的初始屈服强度即塑性应变为0时的应力值，简单计算可得A=666.2 MPa；参数B，n由参数A以及拉伸试验测得的应力、应变数据根据式(2)拟合获得，并且考虑到引伸计在颈缩段剧烈变化时对应变的测定并不准确，参考文献[14]的处理方法，仅采用颈缩前的数据进行拟合，最终获得B=2 365.4 MPa，n=0.974。

参数C可以通过常温动态压缩试验获得。在常温动态压缩试验条件下，式(1)右侧第3项等于1，则式(1)可以改写为

(3)

按照式(3)，绘制应力项随对数无量纲应变速率的变化曲线，固定应变的值即可获得相应的C值，C值为曲线的斜率。计算得到C=0.005。参数m的值可以通过高温动态压缩试验获得。在固定的应变速率下，式(1)可改写为

(4)

按照式(4)，绘制不同试验温度下的对数应力项随对数无量纲温度的变化曲线，固定应变的值即可获得相应的m值，m值为曲线的斜率。计算得到m=2.0。

将由上述数据处理得到的J-C本构模型参数A=666.2 MPa，B=2 365.4 MPa，n=0.974，C=0.005，m=2.0代入式(1)即建立了GH907合金的J-C本构模型。利用该本构模型拟合不同温度和不同应变速率下动态压缩真应力-真应变曲线并与试验曲线进行对比。由图8可知，不同条件下的试验曲线与拟合曲线的塑性段基本一致，说明拟合所得的J-C本构模型能够较好地表征GH907合金的塑性流变行为。

图8 J-C本构模型拟合真应力-真应变曲线与试验曲线对比Fig.8 Comparison between fitting true stress-true strain curves ofJ-C constitutive model and test curves

3.2 失效模型的建立

J-C失效模型[3](也称为失效准则)在冲击数值模拟中应用广泛，该模型将失效应变表述为应力三轴度、应变速率和温度的乘积关系，互不耦合。该模型表达式为

(5)

σ*=σm/σ

(6)

式中：D1，D2，D3，D4，D5为材料常数；σ*为应力三轴度;σm为平均应力;σ为Mises等效应力。

参数D1，D2，D3可以通过参考应变速率(0.01 s-1)和室温(20 ℃)下光滑圆棒试样和缺口试样的准静态拉伸试验获得。在参考应变速率和室温下，式(5)的后2项均等于1，则式(5)可改写为

εf=D1+D2exp(D3σ*)

(7)

根据应力三轴度计算公式，即式(6)，光滑圆棒试样准静态拉伸试验时的应力三轴度为1/3。对于缺口试样，根据BRIDGMAN[16]的研究结果，初始应力三轴度计算公式为

(8)

式中：d0和R0分别为试样缺口截面的直径和缺口处的半径。

失效应变可以采用TENG等[17]的定义，即

(9)

式中：A0和Af分别为试样初始截面面积和断口截面面积。

将拉伸试验数据代入式(8)、式(9)，即可得到失效应变与应力三轴度数据，通过式(7)拟合后，得到失效应变随应力三轴度的变化曲线，如图9所示，拟合参数D1=0.806，D2=-2.38×10-5，D3=6.334。

图9 失效应变与应力三轴度的关系Fig.9 Relationship between fracture strain and stress triaxiality

在室温、同一应力三轴度下，式(5)右侧的最后1项为1，则式(5)可改写为

(10)

通过不同应变速率下的拉伸试验，利用式(10)拟合失效应变与对数无量纲应变速率，拟合结果见图10，获得参数D4=-0.017。

图10 失效应变与对数无量纲应变速率的关系Fig.10 Relationship between fracture strain and logarithmic nondimensional strain rate

在参考应变速率、同一应力三轴度下，式(5)右侧的中间项为1，则式(5)可改写为

εf=[D1+D2exp(D3σ*)](1+D5T*)

(11)

利用式(11)拟合失效应变与无量纲温度的关系曲线，拟合结果见图11，获得参数D5=0.163。将由上述数据处理得到的参数D1=0.806，D2=-2.38×10-5，D3=6.334，D4=-0.017，D5=0.163代入式(5)，即得到了GH907合金的J-C失效模型。

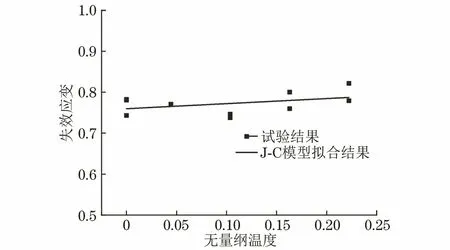
图11 失效应变与无量纲温度的关系Fig.11 Relationship between fracture strain and nondimensional temperature

3.3 本构模型的验证

通过上述分离变量法获得模型的参数之后，通过与试验结果进行比较来验证GH907合金本构模型的有效性是十分必要的，其中有限元数值仿真是一种常用的方法。针对常、高温SHPB压缩试验，在ABAQUS软件中建立与之完全相同的三维几何模型，试验用入射杆、透射杆长度均为1.5 m，直径为14.5 mm；试样尺寸为φ5.9 mm×3.9 mm。考虑到模型的对称性，试验杆与试样均只需建立1/4模型，如图12所示，该有限元模型忽略了撞击杆，选择直接在入射杆的端面施加均布的应力脉冲，脉冲的大小来自实际试验的采集。在对称面施加对称边界条件；压杆和试样之间的接触为硬接触，光滑无摩擦；应变值取自贴于入射杆和透射杆对应位置的单元，与试样接触端面相距60 cm；对接触区域网格进行加密以获得更加准确的结果。霍普金森压杆材料为60Si2MnA弹簧钢，采用线弹性模型，其弹性模量为206 GPa，泊松比为0.29。GH907合金的材料参数采用前文拟合J-C本构模型的数据。

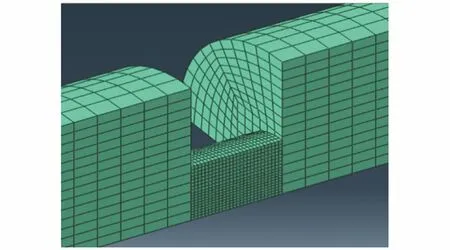
图12 SHPB压缩试验有限元模型Fig.12 Finite element model of SHPB compression experiment

图13给出了试验及仿真得到的3种条件下SHPB压缩时应变速率随时间的变化曲线。由于试样数量的限制，试验与仿真对比研究时未使用黄铜片加以整形来满足常应变速率加载。由图13可以看出，在动态压缩过程中，GH907合金应变速率变化曲线的试验结果和仿真结果在应变速率水平及持续时间上均有较好的一致性。由图14可以看出：在动态压缩过程中，GH907合金真应力-真应变曲线的试验结果与仿真结果非常接近，吻合较好。由表2可以看出，不同温度、不同应变速率下仿真得到的试样几何尺寸和最大应力与试验结果相差很小，相对误差均在2%以内，进一步验证了拟合得到的J-C模型参数的有效性。

表2 试样几何尺寸和最大应力仿真结果与试验结果的对比

图13 动态压缩过程中应变速率变化曲线的仿真结果和试验结果对比Fig.13 Comparison between simulation and test results of strain rate change curves during dynamic compression

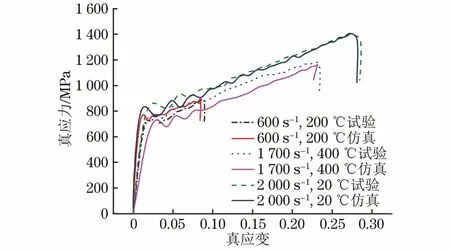
图14 动态压缩过程中真应力-真应变曲线的仿真结果和试验结果对比Fig.14 Comparison between simulation and test results of true stress-true strain curves during dynamic compression

4 结 论

(1) 常温下在0～3 000 s-1应变速率范围内，拉伸时GH907高温合金具有明显的应变速率强化效应，而压缩时对应变速率不敏感。

(2) GH907高温合金在20～400 ℃温度范围内、同一应变速率下动态压缩时产生软化效应。

(3) 基于不同的应变速率和温度下的拉伸和压缩试验数据，拟合得到GH907高温合金的Johnson-Cook(J-C)本构模型和失效模型；利用上述模型对动态压缩过程进行数值模拟，模拟得到的应变速率变化曲线、真应力-真应变曲线与试验曲线吻合较好，试样几何尺寸和最大应力与试验结果的相对误差均在2%以内，验证了拟合所得本构参数的准确性。