超声表面滚压加工纯钛梯度材料的力学性能反演与有限元分析

孙银莎，贾云飞，苑光健，李 晓，张显程

(华东理工大学机械与动力工程学院，承压系统与安全教育部重点实验室，上海 200237)

0 引 言

在工程部件的服役过程中，疲劳、腐蚀、磨损等失效与其材料表面状态息息相关；材料表面强度和质量对其可靠性和服役寿命起着至关重要的作用。近年来兴起的表面强化技术可以在保持实用性和经济性的同时显著延长工程部件的服役寿命。纯钛是一种低密度、高比强度、高耐热的材料，广泛应用于航空航天、石油化工等工业领域[1-2]。纯钛在航空领域主要应用在飞机零部件和航空发动机上。航空航天工业的快速发展对纯钛性能提出了更高的要求；然而，纯钛表面硬度低、抗疲劳性能差的劣势限制了其更广泛的应用[3-4]。

表面强化技术可以改善金属材料的表面质量，提升表面硬度，改善抗疲劳性能，对于工业纯钛等材料的广泛应用有着重要意义。表面强化技术包括激光熔覆、渗氧、渗碳以及表面纳米化技术等，其中表面纳米化技术能够在材料表面制备出一定厚度的纳米晶层，使纳米材料的优势与传统工程材料相结合，从而延长材料的使用寿命[5]。超声表面滚压加工作为一种新兴的超声辅助表面纳米化技术可以同时满足晶粒细化、加工硬化与表面粗糙度等方面的要求[6-7]。在超声表面滚压加工过程中，材料表面因受到工作头的静压力和超声振动的共同作用而发生弹、塑性变形，产生一定深度的塑性变形层；经过往复加工，材料表面的塑性变形层不断加深，晶粒尺寸不断减小，形成典型的表面梯度结构；同时，材料的塑性流动也在材料表面引入了残余压应力，残余压应力的存在有助于降低疲劳裂纹扩展速率，提高疲劳强度。因此，超声表面滚压加工可以提高材料的疲劳强度、耐腐蚀性能和耐磨性能[8]。

表面强化技术制备的表面强化层较薄，厚度一般在几十到几百微米，其力学性能难以用常规检测方法获得。有的研究人员通过将表面强化层剥离下来进行微纳拉伸获得拉伸曲线[9]，但该技术成本高，操作难度大，而且难以获取梯度层不同深度上的应力-应变曲线。如何采用更简单的方法来获取梯度强化层不同深度上的应力-应变关系，已成为表面强化层性能研究的关键问题之一。自20世纪90年代开始，一些研究人员提出了多种纳米压痕反演模型[10]。反演分析方法可以归纳为2种：一种通过对比有限元模拟结果与试验结果，不断调整模拟参数以使模拟结果更接近试验结果，从而获得材料参数。这种方法误差比较大，其准确性取决于输入材料参数是否合理。另一种利用量纲分析，通过一系列量纲函数与有限元模拟结果结合运算，求得材料参数，即利用纳米压痕试验测试的载荷-压入深度曲线，结合相关的特征参量量纲分析技术来获取材料的屈服强度、应变硬化指数等塑性参量。作者采用第二种方法，通过纳米压痕反演分析方法来获取纯钛梯度强化层距表面不同距离处的初始屈服应力和应变硬化指数，进而得到应力-应变关系，并与有限元模拟结果进行对比，以验证反演力学常数的准确性。

1 试样制备与试验方法

试验材料为TA2工业纯钛，化学成分[11](质量分数/%)为0.41C，0.17Al，0.11Si，0.26Fe，余Ti。取尺寸为80 mm×80 mm×6 mm的平板试样进行750 ℃保温2 h热处理，再进行超声表面滚压加工，进给速度为3 000 mm·min-1，工作头振幅为16 μm、频率为20 kHz、静压力为470 N，往复加工30遍。

采用线切割法切取包含超声表面滚压加工面在内的尺寸为5 mm×8 mm×6 mm的长方体试样，研磨抛光后，在试样侧面距表面距离分别为30，60，90，140，200，300，500，700 μm处选取纳米压痕测试点，采用Agilent Nano Indenter G200型纳米压痕仪进行纳米压痕试验。压头采用三棱锥形Berkovich金刚石压头，棱面与中心线夹角为65.3°，棱边与中心线夹角为77.05°，最大载荷为100 mN，加载速率和卸载速率均为10 mN·s-1。为了避免相邻压痕的应力场交叠而影响测试结果，相邻压痕之间的距离均大于10倍压痕深度。相同测试条件下至少测试3次，取平均值。

取截面金相试样，采用金相镶嵌机进行热镶，并经打磨抛光处理，使用由体积比为1…2…17的HF、HNO3和H2O组成的溶液腐蚀45 s后，采用蔡司Observer.Alm倒置式光学显微镜观察截面显微组织。使用JEM-2100型透射电子显微镜(TEM)观察超声表面滚压加工后表面及截面微观形貌。为了获得试样厚度方向的残余应力大小，采用电解腐蚀法进行剥层处理，电解液为10%高氯酸+90%甲醇溶液(体积分数)。电解腐蚀后将试样在丙酮溶液中进行超声清洗，再用酒精冲洗并吹干，采用Proto-iXRD MG40P FS STD型残余应力测试仪测定残余应力。重复上述剥层和残余应力测定工作，即可得到超声表面滚压后试样表面到次表面的残余应力场。

2 纳米压痕反演方法与有限元模拟方法

2.1 纳米压痕反演模型

弹塑性材料典型的纳米压痕载荷-压入深度曲线见图1[12-13]。图1中：P为载荷；h为压入深度；C为加载段曲率；Pmax为最大载荷；S为弹性接触刚度；hr为残余压痕深度；Wt为总功；We为弹性功；Wp为塑性功；Pu为卸载载荷；hm为最大压入深度。根据经典的Oliver-Pharr模型[14]，材料的纳米压痕硬度可以表示为

图1 弹塑性材料典型的纳米压痕载荷-压入深度曲线Fig.1 Typical nanoindentation load-indentation depth curve forelasto-plastic materials

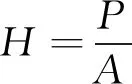
(1)

式中：H为纳米压痕硬度；A为载荷P下的投影接触面积。

等效弹性模量的求解公式为

(2)

(3)

式中：E和ν分别为试验材料的弹性模量和泊松比；Ei和νi分别为压头的弹性模量和泊松比；Er为等效弹性模量；β为压头非对称的修正系数，Berkovich压头取1.034[15]。

对于大多数应用在工程领域的纯金属与合金材料，可以用幂律关系估计其单轴应力-应变关系[13]，该关系表达式为

(4)

σy=Eεy

(5)

ε=εy+εp

(6)

式中：σ为应力；ε为应变；σy为初始屈服应力；εy为初始屈服应变；εp为超过屈服应变之后的塑性应变；n为应变硬化指数。

由式(4)、式(5)、式(6)可知，只要知道初始屈服应力和应变硬化指数就可以确定材料的塑性性能。在纳米压痕测试中，对某一种特定材料的本构关系的描述服从其特殊的无量纲函数形式。DAO等[13]经过量纲分析及系列研究获得如下5个函数：

(7)

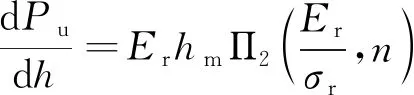
(8)

(9)

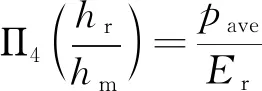
(10)

(11)

式中：σr为代表性应力；εr为代表性应变；pave为硬度；П为无量纲函数。

联立式(4)以及式(7)～式(11)，代入由纳米压痕试验获取的各参数，即可得到初始屈服应力和应变硬化指数。将初始屈服应力和应变硬化指数代入式(4)，即可得到单轴应力-应变曲线。

2.2 纳米压痕试验有限元模拟

对超声表面滚压加工后的表面梯度结构纯钛试样的纳米压痕试验进行有限元模拟。为了简化模型、缩短计算时间，采用二维轴对称结构进行建模，压头作用于结构中心位置处，如图2所示。采用二维四边形单元进行网格划分，节点数为12 940，单元数为12 761，在靠近压痕处采用加密网格以获得更精确的结果，其他地方采较疏网格以减少运算量。纳米压痕试验采用的是Berkovich压头，按照接触面积等效原则，模拟时采用等效锥角为70.3°的刚性锥形压头代替。工业纯钛的泊松比为0.32，弹性模量由纳米压痕试验测得，模拟时使用的不同深度的应力-应变曲线，由前文纳米压痕反演方法获取材料参数后推导得到。模拟时采用载荷控制，最大压入载荷为100 mN。

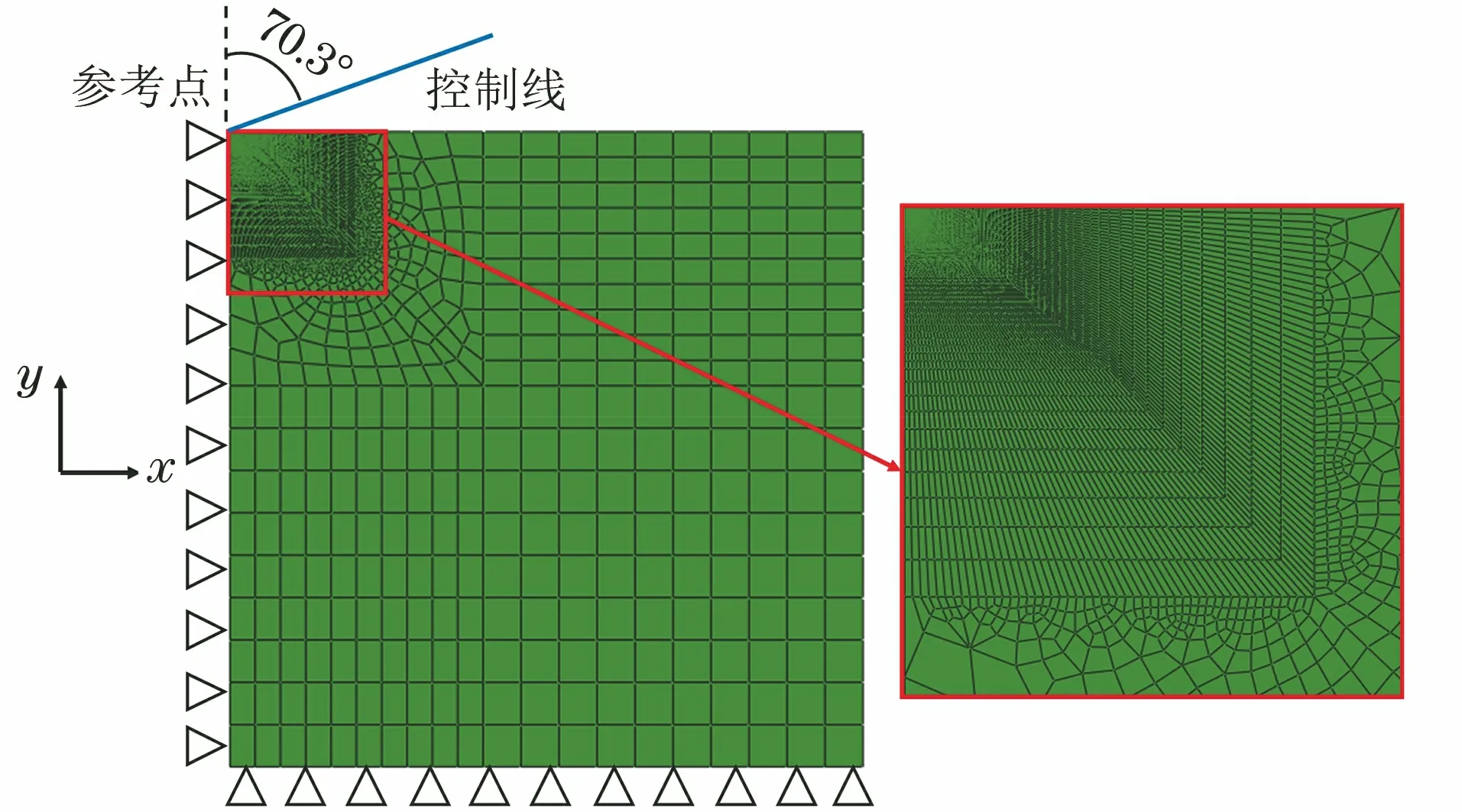
图2 纳米压痕试验有限元模型Fig.2 Nanoindentation test finite element model

经不同工艺超声表面滚压加工后，表层材料初始屈服应力相同时可能会有不同的应变硬化指数，或者初始屈服应力不同时有相同的应变硬化指数。为此，利用有限元模型进行参数化分析，通过改变初始屈服应力和应变硬化指数研究了载荷-压入深度曲线加载段曲率、塑性功与总功之比以及初始刚度的变化规律。

3 结果与讨论

3.1 截面显微组织

由图3可以看出，与具有均匀晶粒的原始试样相比，超声表面滚压后试样表面出现明显的塑性变形层，表面晶粒细化，已无法用光学显微镜观察，其变形形式在微观结构上呈现为梯度分布。最表层由于直接与加工头接触，因此首先发生塑性变形，随着滚压加工时间和遍数的增加，其塑性变形量不断增加。

图3 超声表面滚压加工前后试样的截面显微组织Fig.3 Microstructures on cross section of samples before (a) andafter (b) ultrasonic surface rolling processing

由图4可以看出：在距表面450 μm处，试样的晶粒内产生一定量的位错缠结区，并且位错分布不均匀；在该位置，超声表面滚压加工的影响略小，材料发生一定程度的塑性变形，位错胞处于形成的初始阶段。在距表面300 μm处，试样组织中出现了由一列列排序规整的位错墙构成的亚晶结构，并且晶粒尺寸相比于距表面450 μm处明显减小；亚晶组织是由位错缠结造成的。与距表面450 μm处相比，距表面300 μm处的材料塑性变形显著增大。在塑性变形过程中，微区位错不断发生湮灭和再生，进而形成位错墙结构。事实上，位错胞就是此类位错墙不断分割而组成的。位错胞的胞壁在分割后会继续滑移和湮灭重组，最终会组成图4(b)中亚晶结构的初始状态晶界。因此，在塑性变形显著增加的前提下，纯钛材料的原始组织通过位错胞的胞壁不断湮灭重组，被分割形成大量的亚晶结构。距表面70 μm处的晶粒尺寸相比于距表面300 μm处进一步减小，这是由于越接近表面，超声表面滚压加工的影响越大，发生的塑性变形越大，位错胞的胞壁湮灭和重组现象就越为明显，晶粒细化程度也更高。试样表面的晶粒尺寸已经达到纳米级(80 nm)，且晶粒为等轴晶形态。

图4 超声表面滚压加工后试样截面不同位置和表面的TEM形貌Fig.4 TEM micrographs at different locations on cross section (a-c) and of surface (d) of samples after ultrasonic surface rolling processing:(a) at 450 μm from surface; (b) at 300 μm from surface and (c) at 70 μm from surface

综上可知，经超声表面滚压加工后，纯钛试样从表面至次表面发生的塑性变形程度减小，晶粒由纳米晶向亚晶转变。

3.2 残余应力

在超声表面滚压过程中，表层材料发生塑性变形，并且材料表面的塑性变形程度远大于次表面与基体材料。这种塑性变形量的不同会造成内部结构的约束作用，从而产生内应力。由图5可以看出，从试样表面到内部，残余压应力先增大，至次表面后逐渐减小，次表面处的残余压应力最大,约为326 MPa。虽然超声表面滚压后表面材料发生的塑性变形量最大，但由于表面较自由，受到的约束较小，可以释放一定量的残余应力，因此最大残余压应力未出现在表面，而是出现在次表面处；从次表面到基体，材料受到的超声表面滚压作用减小，塑性变形量降低，因此残余压应力不断减小。

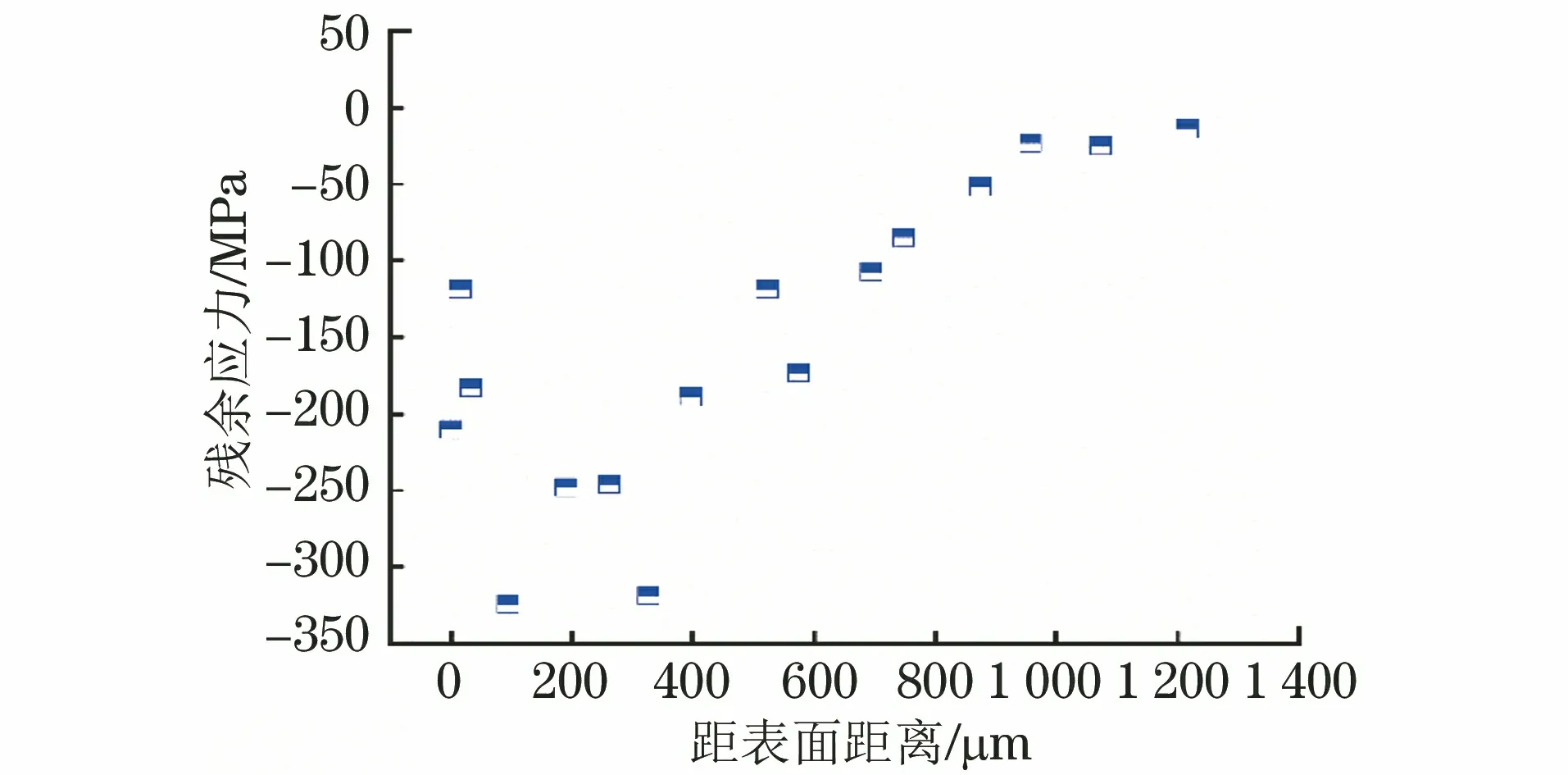
图5 超声表面滚压加工后试样中残余应力随距表面距离的变化Fig.5 Variation of residual stress with distance from surface ofsamples after ultrasonic surface rolling processing

3.3 纳米压痕力学性能及反演应力-应变曲线

由图6可以看出，经相同载荷的超声表面滚压加工后，试样的纳米压痕最大压入深度随着距表面距离的增加而增大。这是由于经超声表面滚压加工后，表面层(深度30～90 μm)形成了纳米晶结构，抵抗变形能力较高，纳米压入深度较浅；随着距表面距离的增大，试样的晶粒尺寸增大，抵抗变形能力减弱，纳米压入深度变深。对于纯钛基体材料(距表面700 μm处)来说，由于本身强度较低，抵抗变形能力相对较弱，因此压入深度比较大。

图6 超声表面滚压加工后试样距表面不同距离处的纳米压痕载荷-压入深度曲线Fig.6 Nanoindentation load-indentation depth curves at different distances from surface of samples after ultrasonic surface rolling processing

由表1可以看出，超声表面滚压加工后，试样的弹性模量随距表面距离的变化规律不明显，距表面90 μm处的弹性模量最大，为121.9 GPa，距表面700 μm处的弹性模量最小，为115.7 GPa，最大值与最小值之间的差距也并不悬殊。弹性模量变化不大说明超声表面滚压加工对工业纯钛微观结构造成的损伤较小。超声表面滚压加工后，试样表层的纳米压痕硬度明显增大，表层最高硬度达到2.625 GPa，与远离表层的基体材料(硬度2.018 GPa)相比，提高了约30%。超声表面滚压加工后纯钛试样表层晶粒明显细化，显微硬度也得到大幅度提高，符合Hall-Petch理论[16]。此外，根据位错理论，材料的塑性变形导致大量的位错运动，引起位错的切割和增殖，并且伴有微观结构缺陷，如间隙原子以及层错等缺陷；这些缺陷会大大阻碍位错的运动，在宏观层面上表现为材料产生加工硬化，因此纳米硬度增加。

表1 超声表面滚压加工后试样距表面不同距离处的纳米压痕弹性模量与硬度

结合量纲分析和纳米压痕数据得到超声表面滚压加工后纯钛试样的塑性材料参数，如表2所示。将弹性模量、初始屈服应力和应变硬化指数代入式(4)，即可绘制得到试样距表面不同距离处的应力-应变曲线，如图7所示。由图7和表2可以看出，随着距表面距离增加，应变硬化指数逐渐增大，表层应变硬化指数较小，在相同应变下产生的应力更大，均匀变形能力较差。

表2 超声表面滚压加工后试样距表面不同距离处的塑性材料参数

图7 由反演方法得到试样距表面不同距离处的应力-应变曲线Fig.7 Stress-strain curves at different distances from surface ofsamples obtained by inversion method

3.4 反演方法的验证

将由纳米压痕反演方法得到的应力-应变曲线引入有限元模型，模拟得到纳米压痕载荷-压入深度曲线，并与试验获得的曲线进行对比。由图8可以看出，试样距表面不同距离处的载荷-压入深度试验曲线与模拟曲线基本吻合，模拟得到的最大压入深度与试验得到的最大压入深度相比，相对误差均在8%以内，可见反演方法是可行的。误差产生的主要原因在于：一是反演采用的方法是基于量纲分析的，计算步骤繁多，反演得到的初始屈服应力和应变硬化指数存在一定误差；二是有限元模拟时输入的材料参数不够全面，而且网格数量有限，与实际情况相比存在误差。

图8 试样距表面不同距离处的载荷-压入深度试验曲线与有限元模拟曲线的对比Fig.8 Comparison of test curves with finite element simulation curves of load vs indentation depth at different distance from surface of samples

3.5 初始屈服应力和应变硬化指数对载荷-压入深度曲线的影响

由图9可以看出，随着初始屈服应力和应变硬化指数增大，载荷-压入深度曲线加载段曲率逐渐增大，塑性功与总功之比逐渐减小，初始刚度变化不明显。在纳米压痕试验过程中，随着工作头压入深度的增加，材料先发生弹性变形，随后发生塑性变形。初始屈服应力和应变硬化指数越大，说明材料抵抗变形的能力越强，施加同样载荷的压入深度越浅，因而加载段曲率越大。在纳米压痕卸载过程中，初始屈服应力和应变硬化指数越大，残余应力越大，材料弹性恢复做功更多，因而塑性功与总功之比越小。初始刚度变化不大，因为对于同样几何形状的压头，初始刚度与回弹量呈正比关系[17]。

图9 初始屈服应力和应变硬化指数对应的纳米压痕载荷-压入深度曲线参量对比Fig.9 Comparison in nanoindentaion load-indentation depth curve parameters for different initial yield stresses and strain hardening exponents: (a) loading curvature; (b) ratio of plastic work to total work and (c) initial stiffness

4 结 论

(1) 超声表面滚压加工后，纯钛试样表面形成了塑性变形层，并形成了从表面到次表面晶粒逐渐增大的梯度结构，最表层晶粒达到了纳米尺度；残余压应力随着距表面距离的增加先增大后减小，在次表面处残余压应力最大。

(2) 超声表面滚压加工后，随着距表面距离的增加，试样的纳米压痕硬度逐渐减小，在相同载荷下的最大压入深度逐渐增大；随着距表面距离的增加，由反演方法得到的初始屈服应力和应变硬化指数分别呈现逐渐减小和逐渐增大的变化趋势。

(3) 将反演方法得到的应力-应变曲线引入有限元模型，模拟得到的纳米压痕载荷-压入深度曲线与试验得到的曲线基本吻合，最大压入深度相对误差在8%以内，说明反演得到的数据较为准确；随着初始屈服应力和应变硬化指数的增大，载荷-压入深度曲线加载段曲率也逐渐增大，塑性功与总功之比逐渐减小，初始刚度变化不明显。