P92钢的蠕变-疲劳损伤行为及蠕变-疲劳损伤本构模型的建立

曹 宇，崔 鑫，纪冬梅

(1.上海电力大学能源与机械工程学院，上海 200090；2.国电南瑞科技股份有限公司，南京 211106)

0 引 言

为了减少煤耗及污染物排放，我国正在建设高效超超临界燃煤机组。超超临界机组在实际服役过程中不仅需要承担基本载荷[1-2]，还需要参与调峰任务，这使得其高温部件面临着比常规超临界机组更高温度及压力的考验。P92钢因具有良好的抗氧化、抗蠕变和抗疲劳等性能[3-4]而成为超超临界机组主要高温部件的首选材料。高温部件在服役过程中承受着静载荷和交变载荷作用，会发生疲劳、蠕变以及二者交互作用导致的失效[5]。因此，仅对P92钢进行简单的高温条件下蠕变性能研究以及寿命预测是片面的、不符合实际工程要求的，而应该在综合考虑各方面因素的前提下对蠕变、疲劳性能进行研究，以更好地确保相关设备的稳定、安全运行。目前，学者们对P92钢的组织和性能、蠕变-疲劳失效机理以及本构模型进行了广泛研究[6-11]，获得了很多重要的结论，为超(超)临界机组的安全运行提供了重要支撑。

自20世纪90年代开始，为了更加精确地预测高温结构的变形，学者们对Chaboche随动硬化模型进行了改进。具体的改进措施包括：引入加载频率，建立新的损伤演化模型[12]；考虑循环载荷作用下的加工硬化因素，建立Lemaitre-Chaboche非线性随动模型[13]；在等向强化和Lemaitre-Chaboche非线性随动强化理论的基础上对背应力进行修正，利用Mises屈服准则建立不同工况下非线性混合强化材料模型的弹塑性应力-应变本构关系[14]；基于Chaboche随动硬化和Voce非线性各向同性硬化理论建立新的混合硬化模型[15]；基于Chaboche混合强化模型和单轴双面模型提出适用于描述铝合金材料循环力学响应的本构模型[16]；在Haddad理论、Paris公式和Chaboche疲劳损伤累积理论的基础上，建立Chaboche-Paris全寿命模型[17]；结合单轴应力、应变的本构关系与非比例加载影响的等效应变得到等效应力，与Chaboche非线性累积损伤模型相结合，推导出多级加载的Chaboche疲劳损伤累积公式[18]；在Chaboche黏塑性统一本构理论的基础上，利用Ohno-Wang模型修正，同时耦合Kachanov损伤演化率建立新的本构模型[19]；利用Chaboche塑性模型和Fatemi-Socie准则，建立缺口构件的多轴疲劳寿命失效模型[20]；在Mises屈服准则和结合Chaboche模型的ISO-KIN强化模型的基础上，建立了不同工况下非线性混合强化材料模型[21]；利用遗传算法[22]、单目标粒子群[23]优化方法获取Chaboche模型中的参数。

超超临界机组主蒸汽温度可达到600 ℃，而目前有关P92钢在600 ℃下的蠕变-疲劳交互行为及其本构模型的研究较少。此外，本构模型的预测能力受到棘轮效应、循环软/硬化、损伤，以及高/低位保载的影响。因此，作者在600 ℃下对P92钢进行应变控制的蠕变-疲劳试验，研究保载时间和应变范围对其蠕变-疲劳性能的影响；在蠕变-疲劳试验基础上，在黏塑性统一本构理论框架下，引入修正的Chaboche非线性随动硬化率及蠕变应变，考虑损伤演化规律，构建了基于Chaboche理论的耦合蠕变-疲劳损伤本构模型。

1 P92钢蠕变-疲劳试验方法及结果

1.1 应力循环试验方法及结果

在P92钢上取尺寸如图1所示的圆柱形标准试样，标距段尺寸为100 mm，在GWT-2504型电子高温蠕变持久试验机上进行应力控制下的蠕变-疲劳试验[24]。试验温度为600 ℃，载荷波形见图2，为高位保载和低位保载两种波形。图2中：σ为加载应力；σmax为最大应力；σmin为最小应力；t为试验时间；th为保载时间。试验时加载的应力水平和保载时间见表1。在加载和卸载的转折处(非长时保载)，应力产生瞬变，为了防止应力瞬变导致的试样断裂，设置了0.03 h的保持时间；该时间对试样产生的影响可以忽略不计，但可以起到缓冲作用。

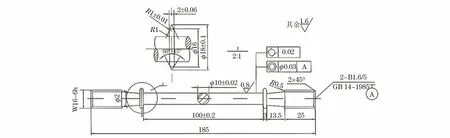
图1 应力控制蠕变-疲劳试验用试样尺寸Fig.1 Sample size for stress controlled creep-fatigue test

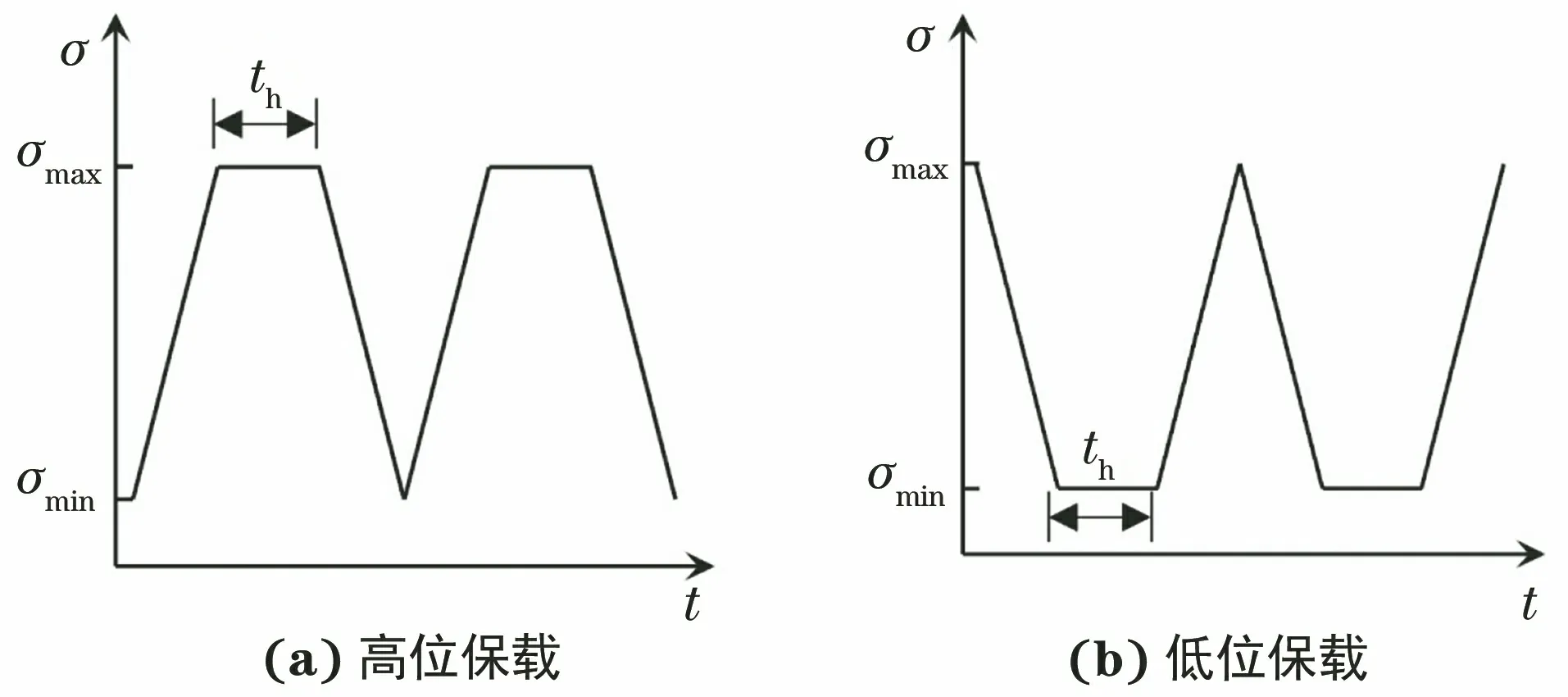
图2 应力控制蠕变-疲劳试验加载波形Fig.2 Load waveforms for stress controlled creep-fatigue test: (a) high load holding and (b) low load holding

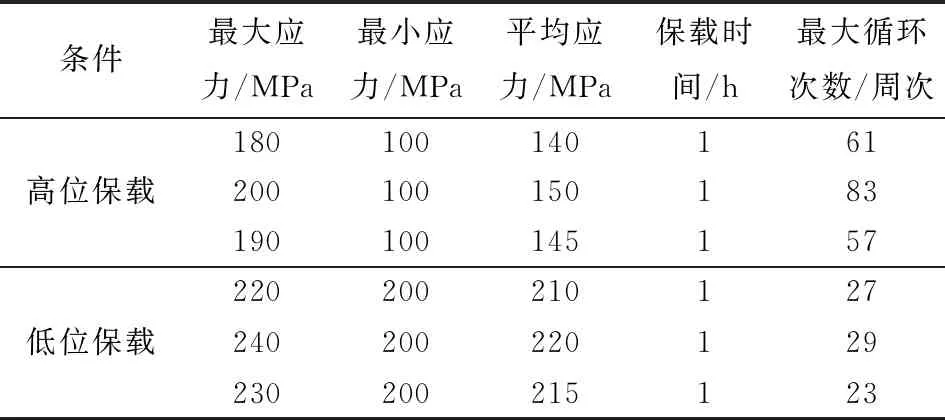
表1 高位保载和低位保载条件下应力控制蠕变-疲劳试验参数

P92钢的损伤可以认为是各向同性的，受损前后的材料在宏观上没有明显区别，很难直接对损伤进行量化表征。目前，主要通过受损后材料弹性模量、密度等物理量的变化间接地确定损伤大小。参考文献[25-26]中有关42CrMo钢的损伤定义，用平均弹性模量的变化来定义损伤变量，其公式为

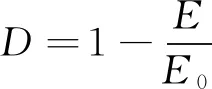
(1)

式中：D为损伤变量；E为每一个循环的平均弹性模量；E0为初始循环的平均弹性模量。

将应变控制蠕变-疲劳试验获取的每一个循环的平均弹性模量代入式(1)，得到不同循环次数下的损伤变量；以损伤变量和归一化循环次数(循环次数N与最大循环次数Nmax之商)作图，得到损伤演化曲线。由图3可以看出：随着循环次数的增加，P91钢的损伤变量先迅速增加，然后逐渐趋于稳定；在稳定阶段，高位保载工况下的损伤变量随着平均应力σm的增大而增大，在低位保载工况下则相反，损伤变量与平均应力成反比。

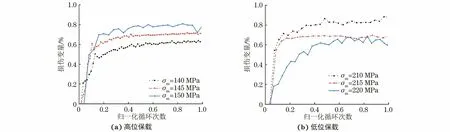
图3 高位保载和低位保载条件下应力控制蠕变-疲劳过程中试样的损伤演化曲线Fig.3 Damage evolution curves of samples during stress controlled creep-fatigue process under high load holding (a) and low load holding (b) conditions

1.2 应变循环试验方法及结果

在P92钢上取尺寸如图4所示的圆柱形标准试样，标距为41 mm，采用MTSlandmark370.10型液压伺服疲劳试验机进行应变控制蠕变-疲劳试验。试验温度为600 ℃，载荷波形见图5，加载和卸载时的应变速率均为10-5s-1。图5中：Δεfat为应变范围；σ为加载应力；ε为加载应力对应的应变；εp为塑性应变；ε1为卸载阶段应力为0时的应变；ε2表示加载阶段应力为0时的应变。试验时的应变范围Δεfat和保载时间th见表2。初期循环对整个寿命有很大的影响，甚至比半寿命处循环的影响还大[27-28]，因此重点研究了初期循环的特点。

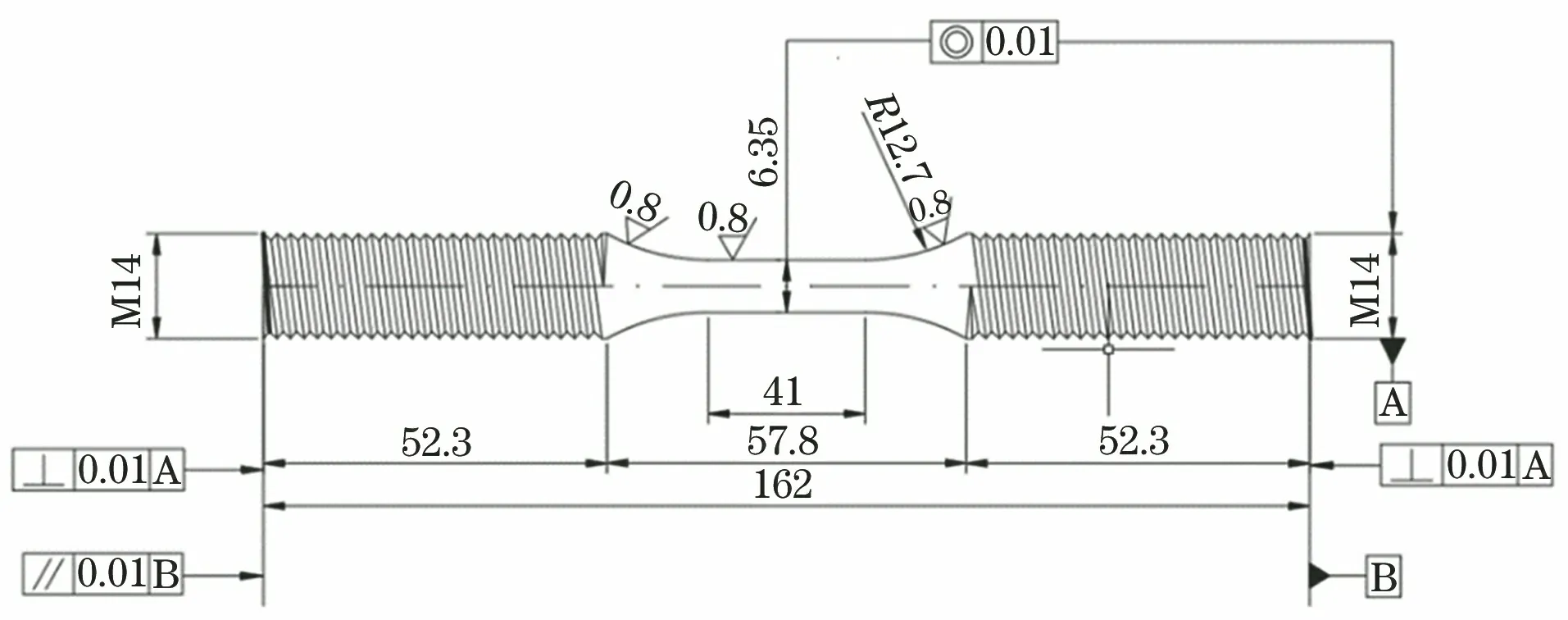
图4 应变控制蠕变-疲劳试验用试样尺寸Fig.4 Sample size for strain controlled creep-fatigue test

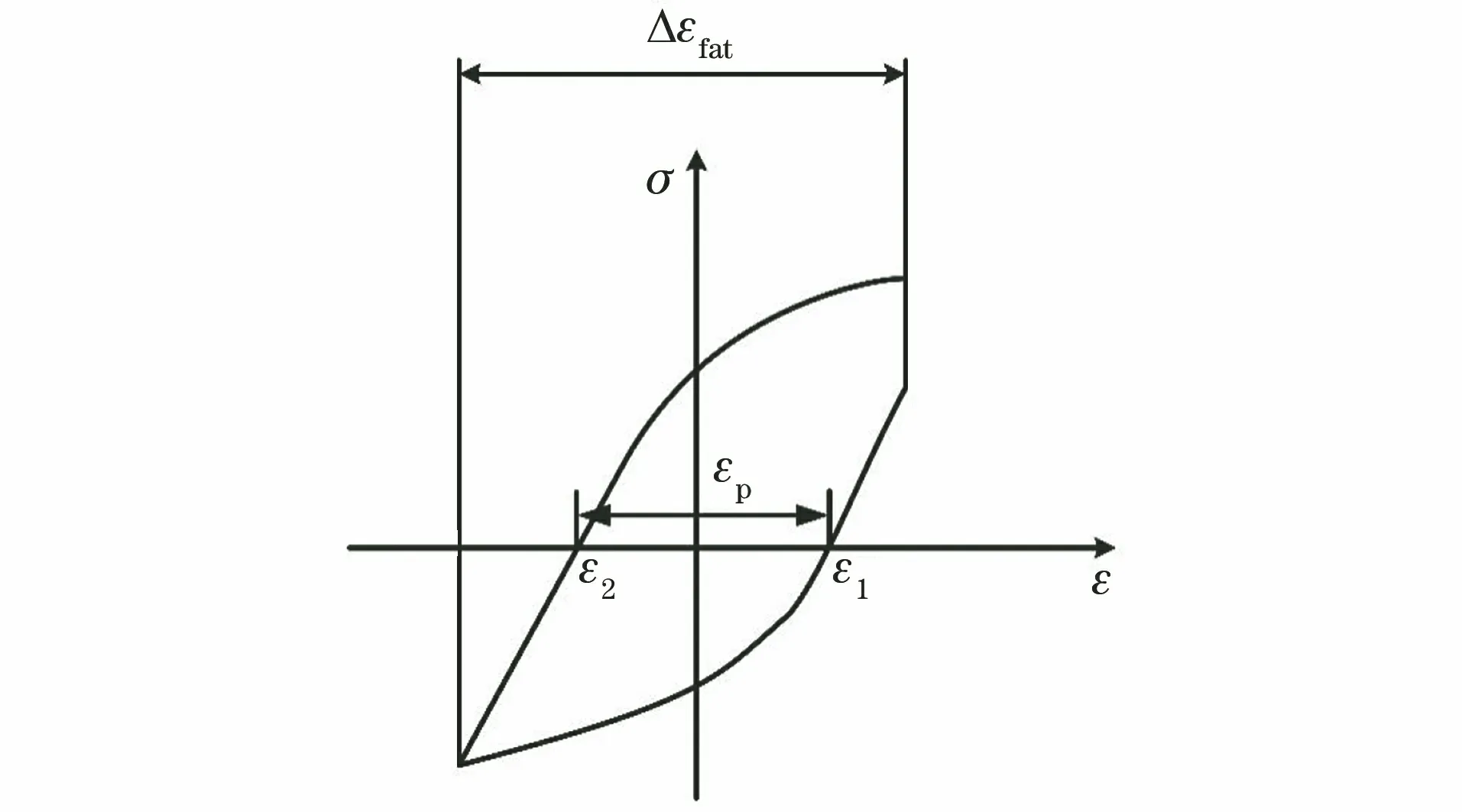
图5 应变控制蠕变-疲劳试验载荷波形Fig.5 Load waveforms for strain controlled creep-fatigue tests

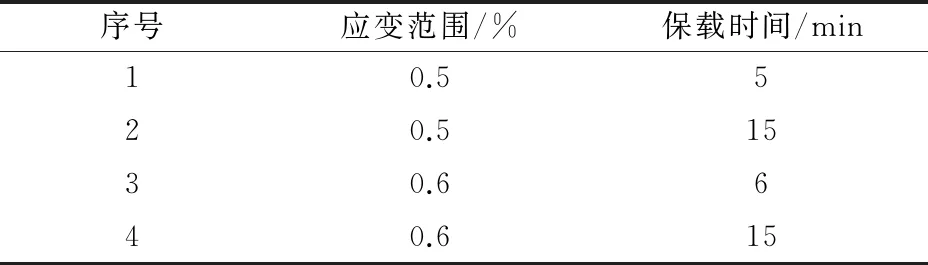
表2 应变控制蠕变-疲劳试验的应变范围和保载时间

塑性应变可有效地反映蠕变-疲劳试验过程中的损伤以及循环硬化/软化行为。应变控制下的塑性应变定义为

εp=ε1-ε2

(2)

由图6可以看出，在应变控制下，塑性应变变化速率随循环次数的增加先快速变化，随后趋于平稳。

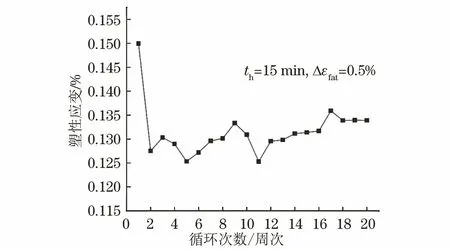
图6 应变控制蠕变-疲劳过程中试样的塑性应变变化曲线Fig.6 Plastic strain variation curve of sample during strain controlled creep-fatigue process

在应变控制蠕变-疲劳试验过程中，P92钢的循环响应可用应力范围随循环周次的变化进行表征，进而可确定该钢的循环硬化/软化行为。应力范围的计算公式为

Δσi=σmax(i)-σmin(i)

(3)

式中：Δσi为第i次循环应力范围；σmax(i)为第i次循环最大应力；σmin(i)表示第i次循环最小应力。

由图7可以看出，在应变控制条件下，试样的应力范围随着循环次数的增加逐渐降低，表现出明显的循环软化特征。

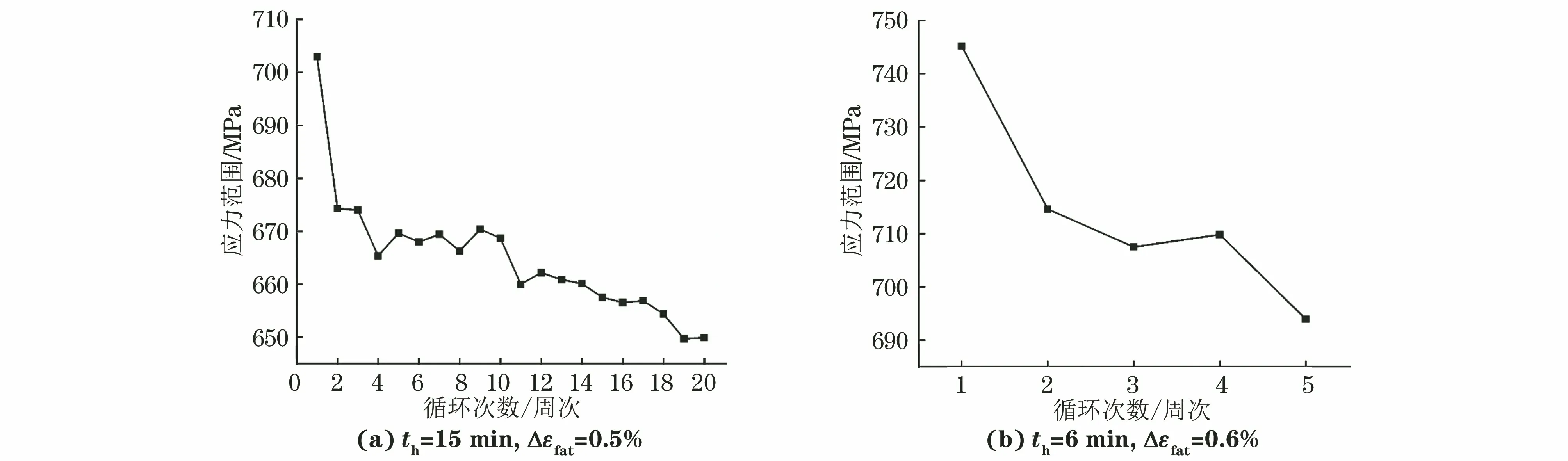
图7 应变控制蠕变-疲劳试验初期试样的应力范围变化曲线Fig.7 Range of stress variation curves of samples at early stage in strain controlled creep-fatigue test

图8 应变控制蠕变-疲劳过程中试样的应力松弛演化曲线Fig.8 Stress relaxation evolution curves of samples during strain-controlled creep-fatigue process

2 耦合蠕变-疲劳损伤的Chaboche本构模型

2.1 主控方程

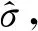
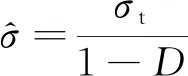
(4)

式中：σt为真应力。

循环黏塑性本构模型的构建需包含屈服条件、应变分解、硬化准则和塑性流动准则4个基本要素，且服从Von Mises屈服准则。金属材料主控方程的具体表达式为

ε=εp+εe+εc

(5)

式中：εe为弹性应变；εp为塑性应变；εc为蠕变应变。

在原有的Chaboche本构模型中引入蠕变应变，其蠕变演化率公式为

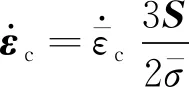
(6)

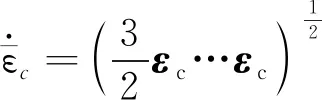
(7)

(8)

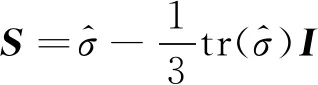
(9)

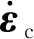
2.2 非线性随动硬化率

线性随动硬化准则无法合理地描述材料在应力控制蠕变-疲劳试验过程中的应力和应变关系，需采用非线性随动硬化准则；该准则最早由Armstrong和Frederick提出，简称A-F模型，是在线性硬化准则的基础上考虑材料硬化的动态恢复效应，加入一个动态恢复项以与逐渐耗散的应变记忆效应发生联系，使得运动硬化法则具有非线性的性质。CHABOCHE[29]对A-F模型中的背应力进行分解，所得模型可以较好地模拟各种迟滞环以及平均应力松弛行为。为了使模型更加精确，作者在Chaboche模型的基础上，将幂函数添加到动态恢复项中，同时为了更好地调控动态恢复项的作用，引入Heaviside函数。改进模型的具体表达式如下：

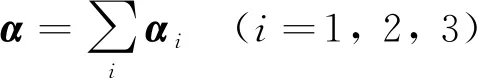
(10)

式中：α为背应力张量；αi为第i个偏背应力张量。

(i=1, 2, …,M)

(11)

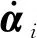
2.3 各向同性软化率

在600 ℃下蠕变-疲劳试验过程中，P92钢具有明显的循环软化特性，然而本构模型中的材料参数ri无法准确地描述这一特性，因此需在模型中引入各向同性硬化准则。目前，在黏塑性统一本构模型中通常采用CHABOCHE[29]提出的非线性硬化准则：

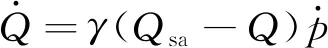
(12)

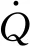
将该软化率引入Chaboche模型，使得模型可以较为合理地描述P92钢的循环软化行为。

2.4 损伤变量演化率

在600 ℃下应力控制蠕变-疲劳试验中，P92钢的峰值应力低于初始屈服应力σs(297 MPa)[24]。采用KANG等[25-26]根据42CrMo钢损伤演化规律提出的演化方程计算损伤变量演化率，该损伤演化方程为

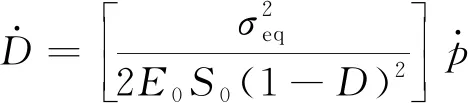
(13)

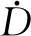
2.5 模型参数的确定

随着黏塑性统一模型的不断改进和发展，模型待求材料参数根据运动硬化内变量的不同而有所差别。虽然待求参数较多，但其求解方法较为容易，通过相关的单轴试验曲线拟合就可以得到。

2.5.1 黏塑性全局参数确定

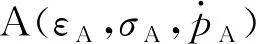
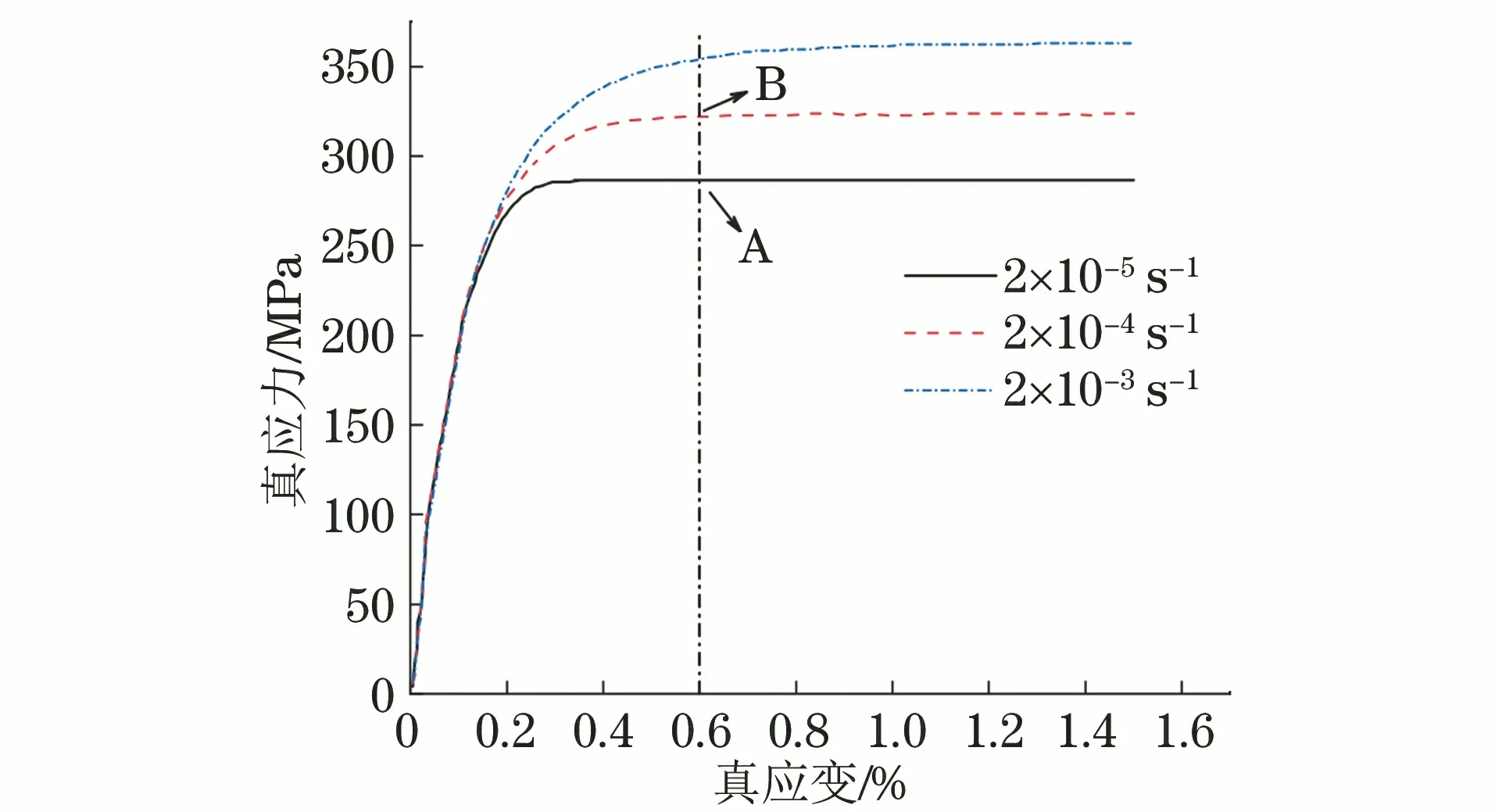
图9 600 ℃不同应变速率下P92钢的拉伸真应力-真应变曲线Fig.9 True stress-true strain curves of P92 steel at different strain rates and 600 ℃ in tension

Δσ=σB-σA

(14)

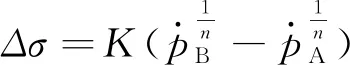
(15)

由于是单向拉伸试验，因此累计塑性应变速率就是塑性应变速率，可由塑性应变-时间曲线求得。采用最小二乘法拟合求得K和n的值。

2.5.2 硬化程度参数的确定

根据Chaboche各向同性硬化准则，应变循环下材料的最大应力与累计塑性应变的关系如下：

σmax=C+Qsa[1-exp(-γp)]

(16)

式中：p为累计塑性应变；C为常数。

根据如图10所示的σmax-p曲线，利用最小二乘法拟合就能够得到Qsa和γ的值。

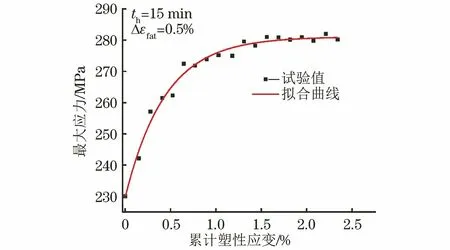
图10 600 ℃下P92钢的最大应力-累计塑性应变关系曲线Fig.10 Maximum stress-cumulative plastic strain curve of P92 steel at 600 ℃

硬化参数ζi和ri可以通过单向拉伸试验曲线来确定。为保证求解的准确性，需要去除各向同性硬化的影响。假定材料的循环软化行为完全由各向同性硬化参量的演化来反映，则可以根据循环硬化的实际演化对单向拉伸结果进行修正。对蠕变-疲劳试验得到的最大应力和累计塑性应变进行拟合；为了提高拟合精度，将原有的幂函数修改为指数函数，得到最大应力和累积塑性应变之间的关系，如下：

σmax=σmax(0)h(p)

(17)

h(p)=1.222 06-0.223 43e-2.275 45p

(18)

式中：σmax(0)为循环第1周次的最大应力。

对于单向拉伸试验，p=εp，则令σ*=σ/h(εp)，得到σ*-εp曲线，基本上可消除各向同性硬化的影响。根据得到的σ*-εp曲线，利用分段线性拟合方法确定ζi和ri，表达式为

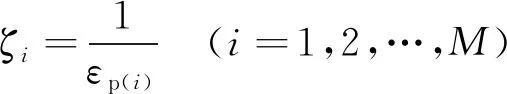
(19)

(i=1，2，…，M)

(20)

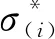
考虑到计算量以及应用的便利性，M取8。

2.5.3 棘轮效应相关参数的确定

m是与材料棘轮效应相关的参数，可使动态恢复项具有非线性，使得迟滞回线具有不封闭性质，从而能够模拟应力控制下的棘轮行为。m值大小影响棘轮应变累积速率，m越小，棘轮应变累积速率越大。m值可以利用应力控制蠕变-疲劳试验数据，采用试错法得到。

综上，得到的模型参数如下：σs=297 MPa，E0=156 GPa，ν=0.33，K=236.2 MPa，n=9，Qsa=51.38 MPa，γ=2.28，m=9，S0=20.52 MPa；ζ1～ζ8依次为2 391.66，1 195.89，607.53，402.81，279.32，139.15，96.88，75.28，73.17；r1～r8依次为9.499，15.911，26.036，22.555，10.088，1.620，6.466，65.550 MPa。

3 模拟结果与讨论

为了验证所构建的本构模型对P92钢循环特性和棘轮行为的预测能力，利用上述得到的本构模型数值解对试验进行模拟，同时将试验结果与求解结果进行对比。

3.1 应力控制下的应力-应变曲线模拟

利用得到的Chaboche模型模拟应力控制蠕变-疲劳试验过程中试样的应力-应变曲线。为了直观清晰地观察比较模拟结果，选取每隔3循环周次的应力-应变曲线。由图11可知，在平均应力140 MPa下模拟得到的应力-应变曲线与试验曲线吻合较好。不同循环周次下模拟所得应力与试验值的最大相对误差均不高于4.90%，如图12所示。

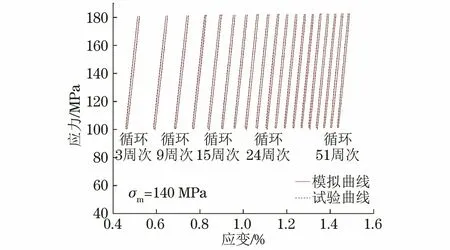
图11 高位保载条件下应力控制蠕变-疲劳过程中试样应力-应变模拟曲线和试验曲线的对比Fig.11 Comparison of simulation curves with test curves of stress vs strain of samples in stress controlled creep-fatigue process under high load holding condition

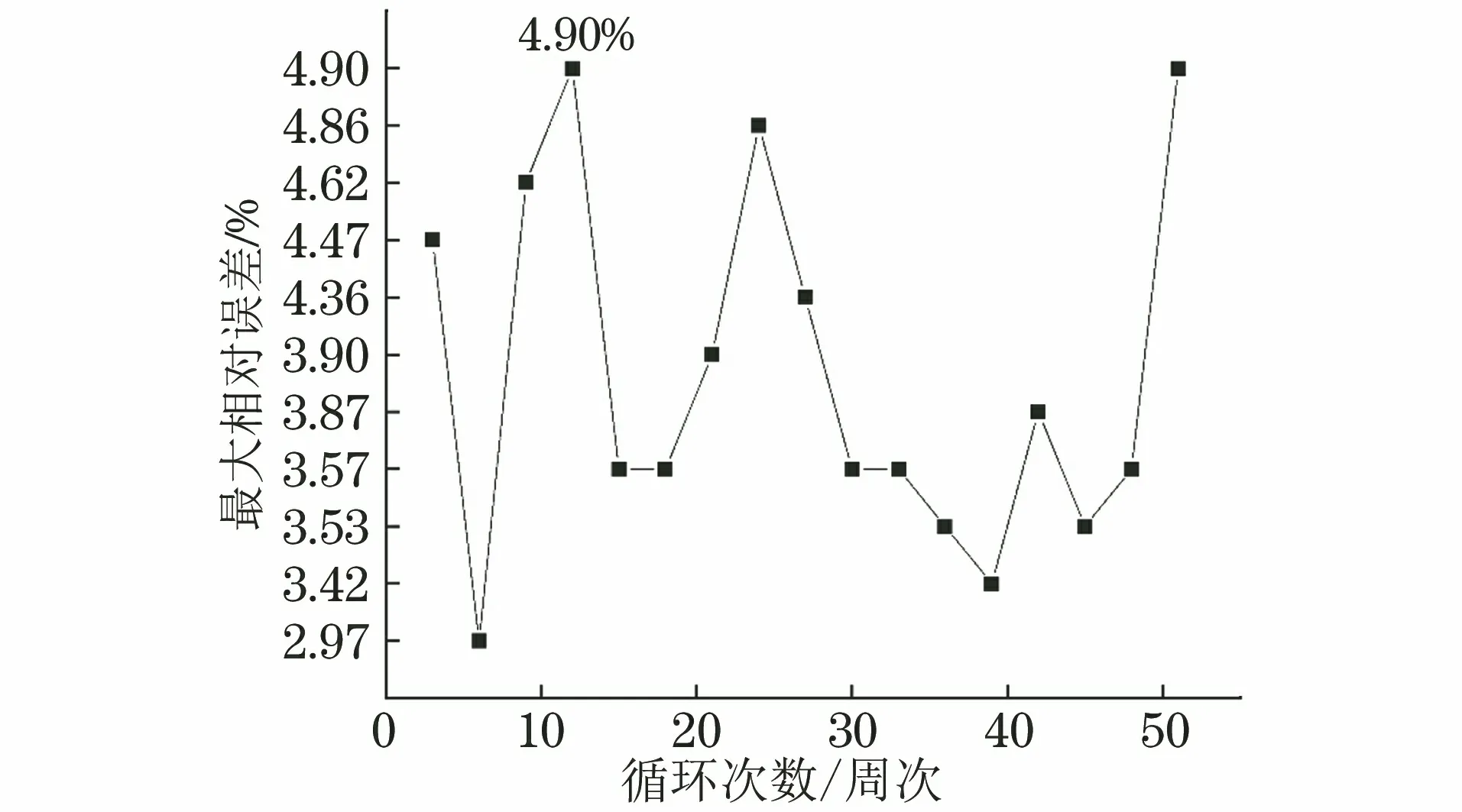
图12 不同循环周次下应力模拟值与试验值的最大相对误差Fig.12 Maximum relative errors of stress simulation and test results at different number of cycles

3.2 应变控制下的应力-应变曲线模拟

利用Chaboche模型模拟应变控制蠕变-疲劳过程中循环1，2周次时的应力-应变循环曲线，并与试验所得曲线进行对比。由图13可以看出，应变控制下，模拟得到的应力-应变曲线与试验曲线吻合较好，最大相对误差为7.30%。因此，可认为该模型可以较好地模拟P92钢在应变控制下的应力-应变曲线。

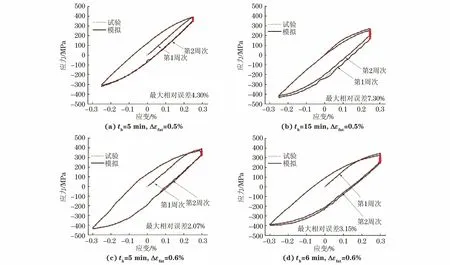
图13 应变控制下蠕变-疲劳循环1，2周次时试样的应力-应变模拟曲线与试验曲线的对比Fig.13 Comparison of stress-strain simulation curves with test curves of samples during creep-fatigue for one and two cyclesunder strain control condition

4 结 论

(1) P92钢在600 ℃下表现出循环软化特性，是一种率相关材料，具有一定的黏塑性特征；在应力控制下，P92钢高位保载的损伤与平均应力呈正相关，而低位保载的损伤与平均应力呈负相关；在应变控制下，P92钢产生应力松弛行为，保载时间越长，应力松弛越明显。

(2) 在黏塑性统一本构理论框架下，引入修正的Chaboche非线性随动硬化率及蠕变应变，考虑损伤演化规律，构建了基于Chaboche理论的耦合蠕变-疲劳损伤本构模型。该本构模型可以很好地模拟P92钢的应力-应变曲线，对应力控制下蠕变-疲劳试验时应力模拟的最大相对误差为4.90%，对应变控制下蠕变-疲劳试验时应力模拟的最大相对误差为7.30%。