基于改进蚁群算法的PID参数优化
2021-10-28郭鹏程张力平
郭鹏程,张力平,赵 顿
(长安大学,陕西 西安 710000)
0 引言
在控制方法中,PID控制器是最早的控制方法之一[1]。PID算法的性能主要依赖于控制参数的优化,传统优化方法有通过专家提供经验、Z-N法和单纯形法。前者依赖于操作者的经验,而后两者中,ZN法的控制过程复杂,普通人员难以操作,单纯形法的超调量大,达到稳定的时间比较长[2]。虽说智能算法已取得了不错的成绩,例如粒子群算法、遗传算法等。其中,粒子群算法以其实现容易、收敛速度快等优点被重视[3]。但还存在一定的缺点。
蚁群算法是基于种群的启发式仿生进化算法,该算法运用的正反馈机制与分布式并行计算机制[4],容易与其他方法相结合,具有较强的收敛性和鲁棒性[5]。本研究采用蚁群算法与模拟退火法融合的算法优化PID参数,不仅克服了传统PID调节的缺陷,还对蚁群算法调节PID进行改进。
1 基本蚁群算法
蚁群算法是由意大利学者M.Dorigo等人提出的,对自然界蚂蚁的寻径方式进行模拟而得出的一种仿生进化算法[6]。较优路径上的信息素浓度越来越高,其他路径的信息素随着时间流逝不断地挥发,最终会形成最优路径。
设蚂蚁数量和城市数量分别为m和n,城市i和j之间的距离为dij,τij(t)表示t时刻城市i和j路径上的信息素浓度。t时刻,蚂蚁k从城市i转移到城市j的概率如下所示:
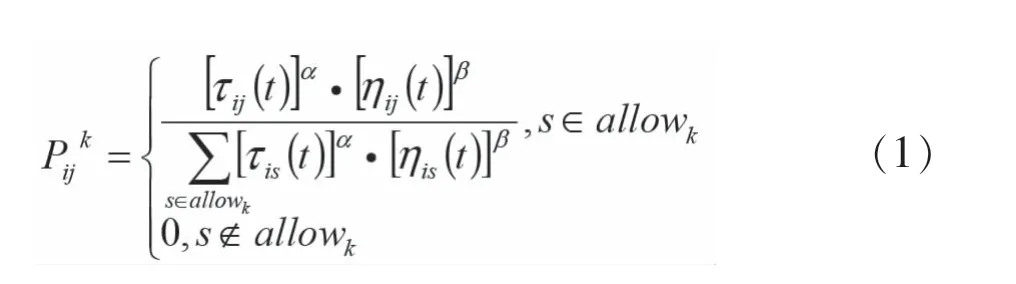
其中,α为信息素重要程度因子;β为启发函数重要程度因子。值越大,搜索随机性减弱,且可能会造成局部最优。
在蚂蚁释放信息素的同时,各个路径的信息素会逐渐消失,所以当蚂蚁完成一次循环后,信息素浓度需实时更新,即:
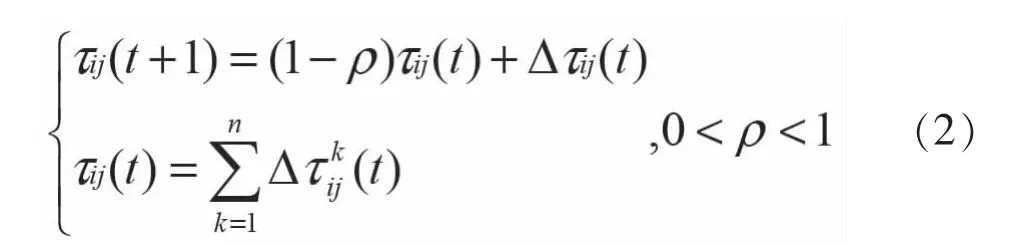
其中,ρ表示信息素挥发浓度,△τij表示所有蚂蚁在路径上释放的信息素之和,△τkij表示第k只蚂蚁在城市i和j的路径上释放的信息素浓度。ρ较小时,则搜索重复路径,直接影响算法的随机性能和全局搜索能力;ρ过大时,则信息素挥发得相对较多,会产生过多无用搜索操作,降低算法的收敛速度。
蚁群算法优化PID的步骤:
1)初始化参数。包括蚂蚁个数、最大迭代次数、信息素蒸发系数、转移概率常数等。
2)随机生成蚂蚁初始位置,计算出适应度值,设为初始信息素,计算状态转移概率。
3)更新位置。对于蚂蚁位置越界采用边界吸收方式进行处理,将蚂蚁位置控制在限定范围之内。
4)更新信息素。
5)满足终止条件,结束搜索过程,输出优化值;不满足,则继续迭代优化。
2 改进蚁群算法的PID参数优化
2.1 优化思想
由以上对蚁群算法的描述,在传统的蚁群算法中,α和ρ的取值固定,会造成在不同时段其重要性无法发挥,影响收敛速度和全局搜索能力。为了在加快收敛速度和避免局部收敛间达到平衡,将模拟退火算法(Simulated Annealing,SA)与蚁群算法相互容纳。模拟退火算法思想利用了实际物理退火的热力学过程中熔融固体粒子的统计热力学规律与数学上求解复杂组合优化问题的类似性[7]。物理退火通过加温过程、等温过程以及冷却过程使粒子热运动减弱,能量下降,得到晶体结构。具体优化方式如下:在每次迭代T中每只蚂蚁i都有初始解FV0,设定初始温度T0=TT0,从领域函数中产生新解FV,并计算目标的差值DC=FV-FV0,DC小于零,则接受新解;DC大于零,则通过Metropolis过程以exp(-DC/T)>rand的概率接受新解,然后退温T0=T0*DS(DS为0~1之间的数),温度未达到条件则重复之前的操作,温度到达则将蚂蚁数目i=i+1;再次进行搜索,一次迭代完成后T=T+1,再次迭代直到迭代结束。具体流程图如图1所示。

图1 优化流程图
2.2 控制系统及目标函数
控制系统结构如图2所示。
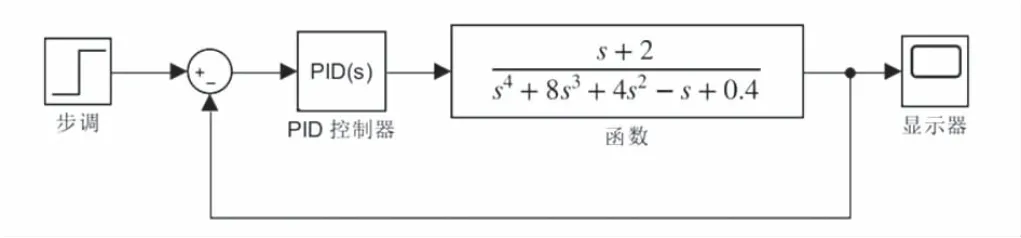
图2 控制系统结构图
3 仿真结果
为了分析算法的可行性,在MATLAB R2018b平台进行仿真测试,在Simulink中建立PID控制模型,建立蚁群算法(ANT)和蚁群与模拟退火融合算法(ANT-SA)的m文件。通过运行m文件调用PID控制系统模型,将PID的参数kp、ki、kd进行赋值,运行PID系统模型并返回目标函数,以便蚁群算法(ANT)和蚁群与模拟退火融合算法(ANT-SA)判断结果优劣,从而找出最优解。
为了验证其性能,从峰值时间tp、超调量δ和调节时间ts这三个方面进行对比。如图3所示。
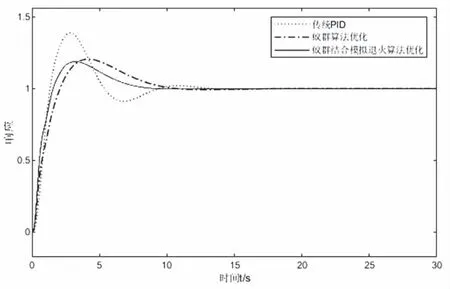
图3 仿真效果图
由图3可知,蚁群模拟退火算法融合调节PID相比使用传统方式调节PID以及蚁群算法调节PID综合性能更加优良。具体仿真参数如表1所示。
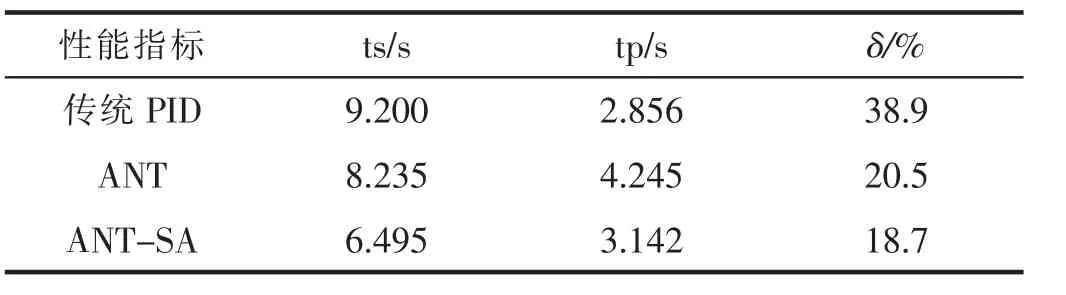
表1 仿真性能
由仿真实验结果可知,与传统PID和ANT调节PID相比,ANT-SA调节PID在超调量和调节时间方面有着明显的优势;在峰值时间上ANT-SA算法调节PID也比ANT调节PID优良,进而验证了蚁群算法和模拟退火算法融合后对PID控制的有效性。
4 结束语
针对传统PID调节方式存在的问题,提出一种将蚁群算法和模拟退火算法融合(ANT-SA)后用于调节PID参数的整定方法,使用MATLAB R2018b/Simulink进行仿真。仿真结果表明,ANT-SA算法在PID调节中体现了超调量小、调节时间短和响应时间较快的优势,控制效果理想。
