基于微分方程算法的光伏并网联络线故障定位方法研究

彭 博，张彩萍

（1.郑州电力高等专科学校，河南 郑州 450000；2.北京交通大学，北京100044）

0 引言

光伏发电作为可再生能源利用的主要形式之一，相比于传统发电机，光伏电站由于自身结构和工作特性，具有间歇性、波动性等特点[1]。故障发生时短路电流特性差异很大，这对光伏电站并网联络线继电保护提出了较大的挑战。

短路暂态特性是研究光伏电站联络线距离保护的基础。文献[2]，[3]建立了基于内部等效参数和外特性电气参数的4种光伏组件故障诊断模型。文献[4]，[5]通过故障仿真，分析了不同短路故障时光伏逆变器的输出特征。文献[6]，[7]利用Matlab/Simulink软件搭建了光伏并网发电系统模型。以上文献通过理论和仿真分析指出：光伏电站联络线在发生对称故障时，光伏电站侧的故障电流较小，而系统侧的故障电流中含有较大的衰减直流分量，使得基频分量的计算结果不准确；在发生不对称故障时，光伏电站输出的短路电流几乎不含基频电流分量，而占比较大的衰减直流分量会使基频分量的计算结果不准确。

对于光伏电站的继电保护，文献[8]分析了光伏电站的弱电源特性会导致联络线的光伏侧电流保护无法启动、差动电流保护灵敏度下降，以及距离保护误动和拒动等问题。文献[9]通过引入线路的短路阻抗，将区内、外故障下线路短路阻抗的大小差异作为保护动作的依据，以防止自适应距离保护对区外故障的误动作。文献[10]，[11]提出了基于保护安装处的正序和负序电流的自适应分支系数计算，并以此为基础确立了距离保护Ⅱ段阻抗整定值。

针对光伏电站复杂的短路电流特性对传统故障定位方法正确动作的影响，本文首先提出一种基于微分方程的故障定位方法，建立了故障前后的暂态过程；然后利用二阶巴特沃斯滤波器对测量电压和电流进行处理，并通过故障前后的节点电压重构，提高了求解微分方程迭代过程的快速性和正确性；最后结合仿真，与传统故障定位方法进行对比，验证了所提故障定位方法的正确性和优越性。

1 输电线路微分方程基本模型

以图1为示意电路，模拟发生单相接地故障时输电线路上的R-L微分方程。其中，F点为故障点，Rf为过渡电阻。

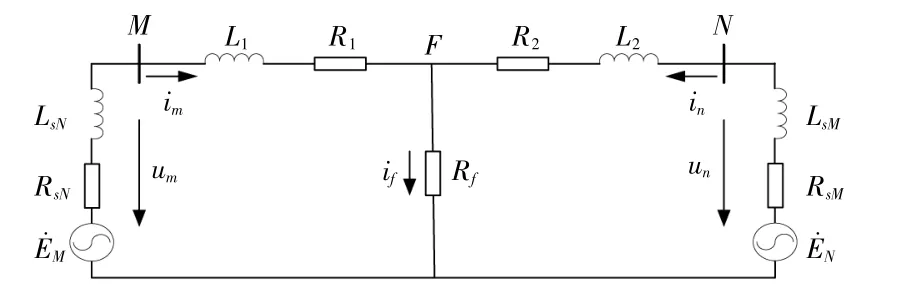
图1 简易模型示意图Fig.1 Sketch map of the simple model

以母线M为例，保护安装处M点测量得到的A相电压为

式（3）通过多点采样和迭代计算得到lf。根据电路理论基本知识，故障点电压vfa（n）是关于Rf的函数，本文将会采用故障点电压重构方法进行计算。

2 输电线路微分方程的求解

2.1 低通滤波

根据国内外对光伏机组故障暂态特性的研究，故障发生时，光伏机组输出的短路电压和短路电流均含有高频分量，这些高频分量会严重影响基于基频分量的故障定位方法的计算精度。因此，构建合适的低通滤波器滤掉高频分量，可以有效提高故障定位计算方法的正确性和有效性。二阶巴特沃斯低通滤波器[12]，[13]具有良好的线性相位特性、便于设计和最大平坦相应的特点，本文建立了如式（4）所示的低通滤波器。

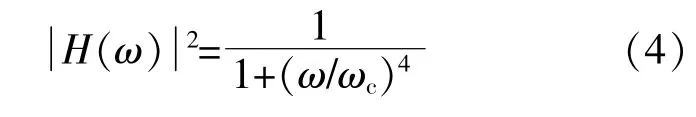
式中：ωc为截止角频率，本文取值为942.477 rad/s，即截止频率为150 Hz。

二阶巴特沃斯滤波器对处理的电气量具有相位延迟效应，考虑到故障定位需要的是阻抗角，即电压和电流的相角差，故只要故障电压和电流流经同一低通滤波器，滤波后的测量阻抗角仍为实际阻抗角。

2.2 故障点电压重构

根据输电线路等传变原理，为保证所有电气量都符合实际参数模型，重构后的故障点电压也应经低通滤波器处理，并且该滤波器的结构应和处理测量电压、电流的滤波器一致。如果重构电压没有经过同样的低通滤波器，一方面会导致相角不一致，另一方面还会引起保护装置的暂态超越等。因此，将故障点重构电压分解为故障发生前的电压和故障发生后的电压两个部分。

式中：vfr为故障点电压；vfr1为故障发生前的故障点处电压；vfr2为过渡电阻上的压降。

vfr1和vfr2的求解分为故障发生前和故障发生后两种情况。

①故障发生前

为求得准确的故障距离，根据迭代算法的基本原理，选取该线路上任一点作为起始参考点，求取正常情况下该点的电压作为故障前重构的起始电压，然后进行迭代计算。起始点电压为

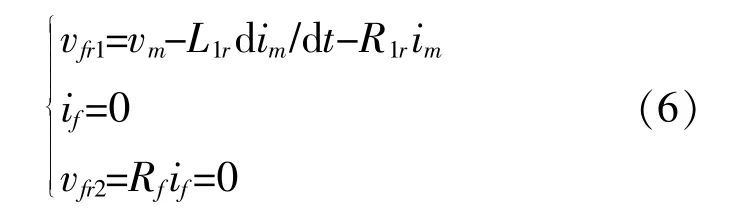
式 中：if为 流 过 过 渡 电 阻 的 故 障 电 流；L1r，R1r分 别为保护安装处到假定故障点的线路正序电感、正序电阻。

②故障发生后

单相接地故障和相间故障的特点有所区别，在故障节点电压重构时也应分别考虑。对于单相接地故障，可以认为故障点量测的零序阻抗几乎相同，故可以近似认为流过Rf上的I0相位和流过m处的I0相位相同，即：

式中：C0为保护安装处零序分流系数。

基 于 上 述 分 析，可 得 式（8），其 中Rfr=C0Rf。

3 基于微分方程算法的故障定位迭代方法

为了提高故障距离的计算精度，须要制定相应的迭代计算方法，实现故障点电压重构，具体步骤如下：

①定义t0和tcal分别为故障发生时刻和采样时刻。设置迭代起始点为线路中点，即liter=0.5lwhole；

②获取各关键电气量，并将得到的各电压、电流流经相同的低通滤波器处理，得到滤波后的电气量采样值；

③结合重构原理，计算各采样点的重构电压值；

④如 果tcal-t0≥T1，其 中T1设 为5 ms，转 至⑤，否则转至⑧；

⑤将tcal-T1～tcal内各电气量的重构值代入式（3）；

⑥通过迭代算法，求解重构差分方程组，得到故障距离lcal，并以此作为下一次迭代的起始点；

⑦如果tcal-t0≤T3（即已迭代总时长，如40 ms），转 至⑧；否 则，转 至⑨；

⑧进行下一次采样，重复②～⑦过程；

⑨迭代结束。

通过上述迭代计算，可得故障发生后一段时间内的故障距离。

4 仿真分析

本节主要研究故障后光伏电站复杂的故障电流特性对联络线保护的性能影响，考虑到故障持续时间较短，故假设光伏电站的辐照强度保持不变。仿真平台采用PSCAD/EMTDC软件，仿真硬件 配 置 为Intel（R）Core（TM）i5.3470 CPU@3.20 GHz，内存容量为4.00 GB，仿真模型如图2所示。

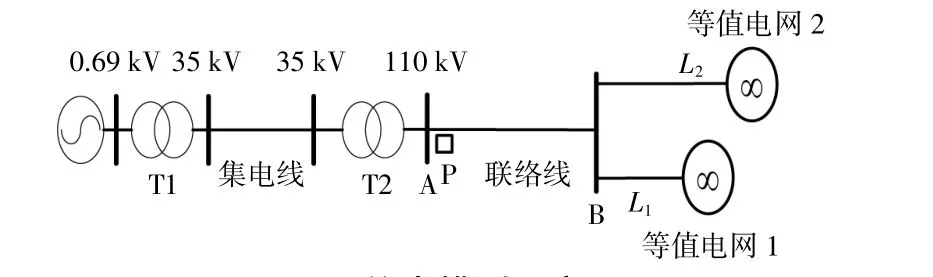
图2 仿真模型示意图Fig.2 Sketch map of simulation model

对于图2仿真模型，在PSCAD/EMTDC软件中选取对应的原件库，建立各元件的连接关系。对于复杂的光伏机组，PSCAD软件中有相应的光伏机组库，将选中的光伏机组与其他元件相连即可。

建模所需的参数包括：光伏电站总的额定容量为100 MVA，额定线电压为690 V；定子绕组电阻、定子漏电抗、转子绕组电阻、转子漏电抗、定转子互感和转子额定转速分别为0.007 56，0.142 5，0.005 33，0.142 5，2.176 7和1.2，均 为 标 称 值。变压器T1的容量、变比、联结组别和漏电抗分别为120 MVA，0.69/35.0 kV，Yn/d和8.95%；变 压 器T2的容量、变比、联结组别和漏电抗分别为120 MVA，35.0/110.0 kV，d/Yn和10.5%；联络线总长度为100 km，正序电阻和电抗分别为0.081Ω/km，0.401Ω/km；零序电阻和电抗分别为0.463Ω/km，1.209Ω/km。此外，系统内线路L1、集电线和L2的阻抗参数与联络线相同，总长度分别为40，50 km和60 km。传统故障定位方法是通过阻抗测量元件比较测量阻抗和整定阻抗的相对大小，来判断故障发生的位置和保护动作的逻辑。因此，阻抗测量元件的计算精度将直接影响故障定位的动作特性。为此，本文通过引入故障距离曲线，一方面验证本文所提算法在区外故障和区内故障的动作性能；另一方面在性能优劣上与传统距离保护方法进行对比。

4.1 区内故障动作性能验证

对于区内故障，本文在联络线上选取了3个故障点，位置分别距该侧母线10，50 km和80 km。分别在这3个故障点，模拟单相AG（AG）、A相经50Ω过渡电阻接地[AG（50Ω）]、BC相间故障（BC）和 三 相 对 称 故 障（ABC），仿 真 结 果 见 图3。

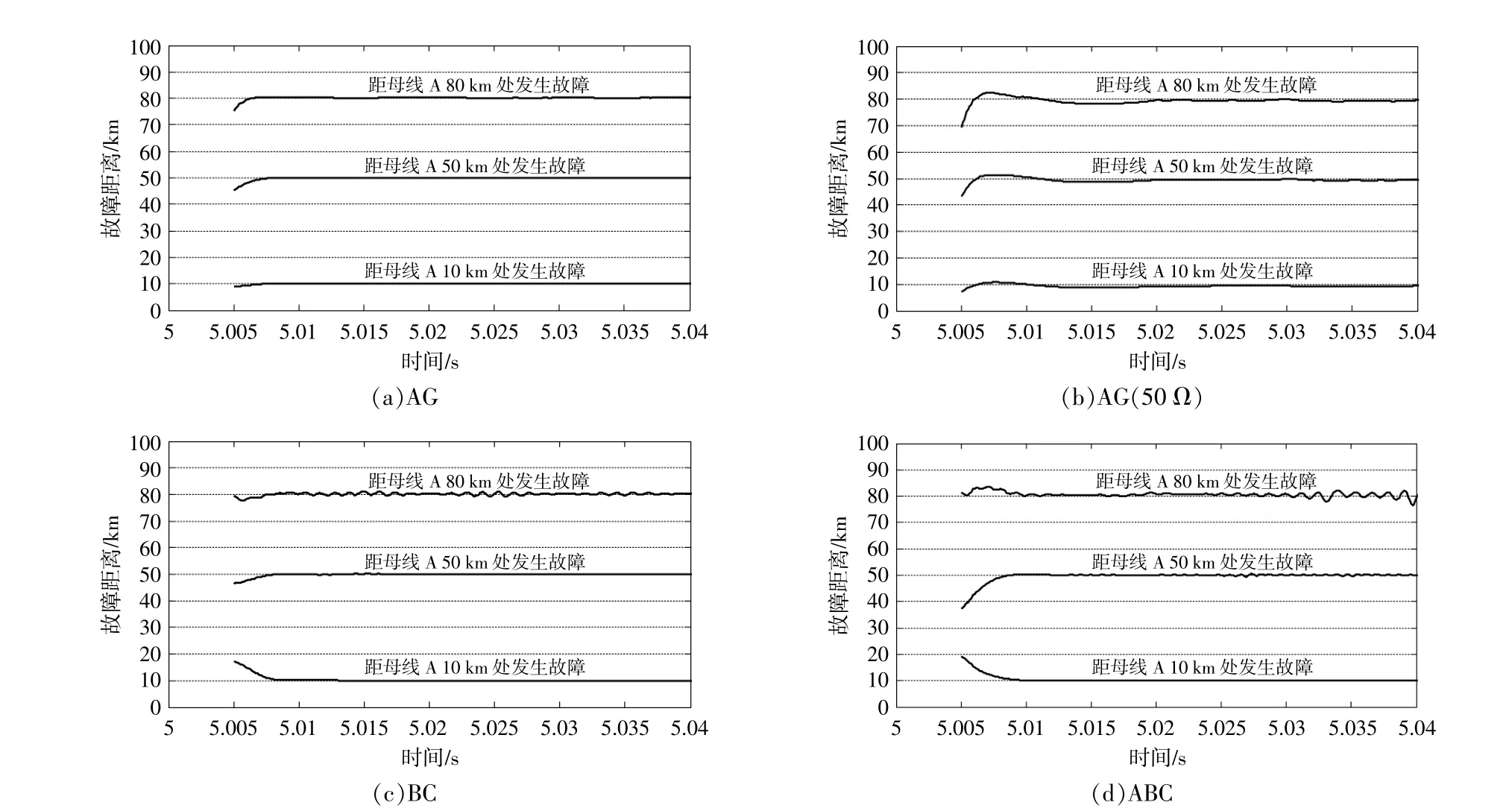
图3 区内故障仿真结果Fig.3 Simulation results of close-zone faults

从图3可以看出，对于区内故障，在3个故障点位置的不同故障类型均可以较快地得到稳定的故障距离，并且仿真得到的故障距离与实际故障点位置几乎一致。仿真结果表明，所提故障定位方法对于区内故障有较好的动作性能。

4.2 区外故障动作性能验证

对于区外故障，在图2中分别设置了F1和F2两个故障点，其中：F1距母线B 10 km处，为正向区外故障点；F2位于变压器T1的高压侧母线附近，为反向区外故障点。

（1）正向区外故障点F1

在F1处模拟了4种不同故障类型，其故障距离仿真结果见图4。由图可以看出，对于正向区外故障，经过短暂的暂态过程后，稳态得到的故障距离均大于实际故障距离（110 km）。这说明当发生正向区外故障时，本文所提方法不会误动作。

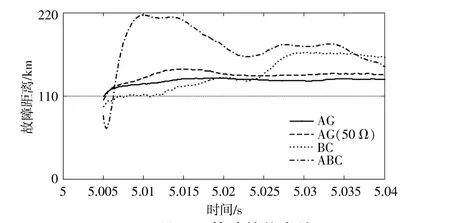
图4 F1处不同故障的仿真结果Fig.4 Simulation results of different faults at F1

（2）反向区外故障F2

对于反向区外故障，本文着重对BC相间故障和三相对称故障开展仿真分析，结果见图5。

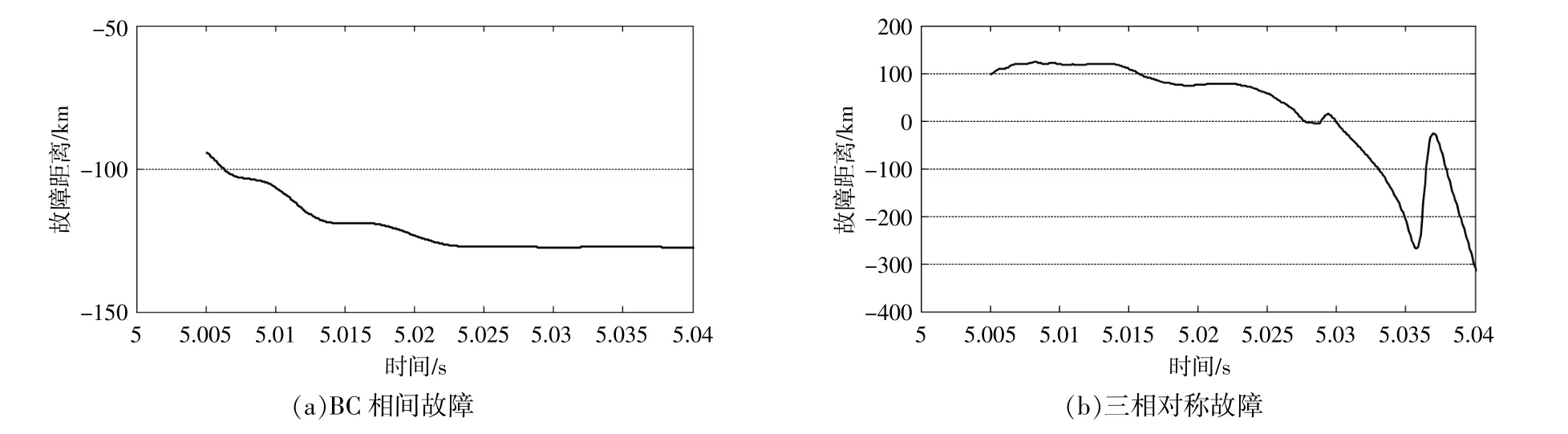
图5 F2处不同故障的仿真结果Fig.5 Simulation results of different faults at F2

由图5（a）可以看出，对于反向区外的BC相间故障，本文所提方法能够得到一个收敛的故障距离值，故障距离比实际故障点位置更远，不会导致本线的距离保护误动作。对于图5（b），反向区外发生三相对称故障时，虽然本文所提方法无法得到一个收敛的故障距离，但得到的故障距离也不会使本线的距离保护误动作。

综上所述，无论是正向区外故障还是反向区外故障，本文所提方法均不会误动作。而对于区内发生不同类型的故障，本文所提方法均能快速收敛出较为准确的故障距离，即能够正确动作。

4.3 与传统距离保护故障定位方法的性能对比

本文选取三相对称和BC相间故障，对所提方法与传统距离保护故障定位方法的性能进行比较。

（1）三相对称故障

假设在0.5 s时刻，图2中的联络线中点位置发生了三相对称故障，图6给出了传统距离保护和本文提出的新型距离保护方法计算得到的故障距离曲线。图6中，曲线1，2和3分别对应本文提出的新型故障定位方法、未经故障点电压重构的微分方程算法和传统故障定位方法。

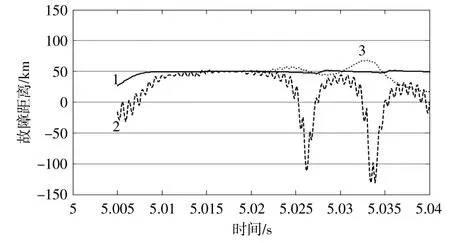
图6 三相对称故障性能对比结果Fig.6 Performance comparison results of 3-line fault

对于曲线1，由于故障时光伏机组输出的衰减直流分量对微分方程算法的影响非常小，并且通过故障点电压重构解决了跨数据窗的问题，因此计算结果的精确度和稳定性很高，收敛速度也够快。对于曲线2，由于缺少故障点电压重构的过程，虽然能短时得到正确的故障距离，但计算结果的稳定性非常差，并且随着时间的推移，计算结果的精度也较为糟糕。对于曲线3，由于传统故障定位方法是基于工频相量，受占比较高的衰减直流分量的影响较大，因此计算结果精度较差，无法满足应用要求。通过对图6中3条故障距离曲线的对比可以看出，对于三相对称故障，本文提出的新型故障定位方法的计算精度和稳定性都更好。

（2）BC相间故障

假设在0.5 s时刻，图2中的联络线中点位置发生了BC相间不对称短路故障，图7给出了传统故障定位和本文提出的新型故障定位方法计算得到的故障距离曲线。图7中，曲线1，2和3分别对应本文提出的新型故障定位方法、未经故障点电压重构的微分方程算法和传统故障定位方法。

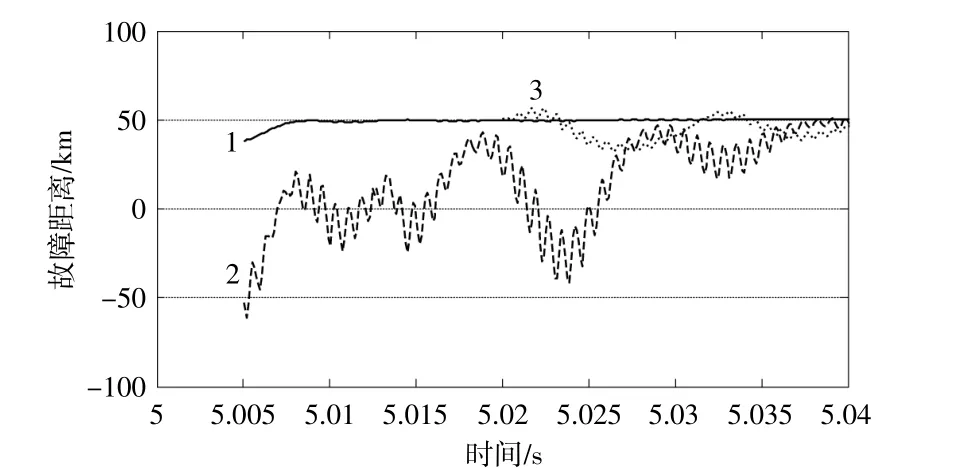
图7 BC相间故障性能对比结果Fig.7 Performance comparison results of BC fault

图7的仿真情况与图6类似：曲线1的计算精度和稳定性都很好，收敛速度很快；曲线2的计算精度较差，并且无法收敛于一个稳定值，这是由于不对称故障使得缺少故障点电压重构的微分方程算法无法得到一个准确的故障距离；曲线3的计算结果精度较差，收敛速度较慢。

综上所述，相比于传统故障定位方法和缺少故障点电压重构的微分方程算法，本文提出的新型距离保护方法计算结果较为精确，稳定性较好，并且收敛速度较快，能够较好地满足工程应用要求。

5 结论

①微分方程算法不受光伏系统运行方式和特殊短路特性的影响，能较好刻画故障前后的电气量变化过程。引入二阶巴特沃斯低通滤波器对测量电压和电流进行处理，消除了光伏机组短路故障馈出的高频暂态分量对计算结果精度的影响。

②将故障点电压分解为故障前和故障后，通过故障点电压重构，对测量电压和电流进行迭代计算，提高了计算结果的有效性和精确性。

③仿真结果表明，所提故障定位方法在区内故障和区外故障均能正确动作，并且相比于传统故障定位方法，所提故障定位方法的整体性能更好，可更好地满足电网安全稳定运行要求。