低计算复杂度模块化多电平换流器电容均压算法

王 录，张新燕，2，周 鹏，岳家辉，邢 琛，童 涛

（1.新疆大学 电气工程学院，新疆 乌鲁木齐 830047；2.可再生能源发电与并网技术教育部工程研究中心，新疆 乌鲁木齐 830047；3.中国航空工业集团公司 第六三一研究所，陕西 西安 710068）

0 引言

模块化多电平换流器（Modular Multilevel Converter，MMC）具 有 低 谐 波、易 于 扩 展 等 优 点，解决了传统电压源换流器（Voltage Source Converter，VSC）耐 压 低、开 关 频 率 高 等 问 题[1]，[2]。

近年，MMC柔性直流输电在可再生能源并网领域得到广泛应用[3]～[5]。文献[6]提出一种基于MMC的光伏并网系统。该系统具有无功补偿功能，在光照变化时仍可以实现稳定运行，提高了太阳能利用率。文献[7]提出了基于模型预测控制的MMC控制方法，并将其应用于海上风场汇流HVDC输电系统，消纳了海上风电，提高了系统的动态响应速度和鲁棒性。由于MMC子模块较多，其级联结构的电容均压问题成为研究热点，目前均压控制主要有排序算法和载波移相技术的均压策略[8]。文献[9]采用最近电平逼近调制（Nearest Level Modulation，NLM）技术，得到桥臂所需投入的子模块数；然后对全部子模块电压冒泡排序，根据桥臂电流方向投入相应数目的电压最大或最小子模块。该算法时间复杂度大，开关器件的投切频率高。文献[10]设置电压上、下限并引入保持因子，增加了未越限子模块保持原有投切状态的概率，降低了开关频率，但须要对所有子模块排序。文献[11]设置组间最大允许偏差值，通过交换投入组与切除组电压越限子模块投切状态，降低了器件的开关频率。文献[12]通过降低排序频率降低了器件的开关频率，但对于排序频率的确定较为困难。文献[13]通过设置一组子模块电压上、下限来控制子模块电压的波动范围，同时降低了器件的开关频率，但存在电压离散度大的缺陷。文献[14]采用最优分解顺序的质因子分解法对子模块进行多层分组排序，降低了排序运算量，所提出的组间电容均衡方法提高了电压一致性。文献[15]引入希尔排序，确定了排序步长的最优选择，进一步降低了排序次数，但优化效率受到分层数的约束。文献[16]采用限制步数的插入排序，对投入组电压序列修正为有序序列，然后进行2路归并排序，算法时间复杂度进一步降低，但均压算法基本均须对全部子模块电压排序，算法时间复杂度仍有改进的空间。

本文基于NLM调制技术，提出了一种时间复杂度较低的电容均压算法。在桥臂工作状态变化时，该算法对所有子模块电压进行希尔排序，而各工作状态下其它控制周期并不对全部子模块电压排序；根据投入组和切除组子模块电压的变化规律，个别子模块开关状态的交换只须以维持投入组或切除组电压的有序性为条件 （对于投入组须要附加限制步数的插入排序），使得下一控制周期子模块投切状态的变动不排序，大大降低了算法时间复杂度与开关频率。引入子模块状态交换偏差值使开关频率、电压波动可根据需要调节，最后在PSCAD/EMTDC中建立单端逆变侧模型，仿真验证本文提出均压算法的正确性和有效性。

1 MMC拓扑结构与传统均压策略

1.1 MMC拓扑结构

本文以工程上广泛使用的半桥子模块结构MMC在光伏并网中的应用为例，两级模块化多电平光伏并网拓扑如图1所示。

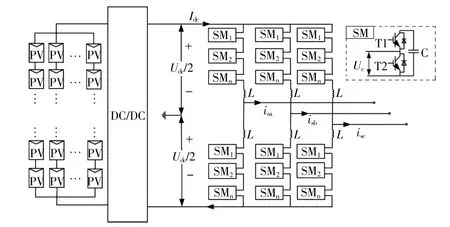
图1 两级模块化多电平光伏并网拓扑结构Fig.1 Two stage modular multilevel photovoltaic grid connected topology

由图1可知，MMC三相中每个相单元包含上、下两个桥臂，n个相同的半桥子模块级联后与桥臂电抗器L串联组成单个桥臂，桥臂电抗器抑制环流。半桥子模块的拓扑结构为图中虚线框所示，通过控制T1，T2两个IGBT，得到投入、切除和闭锁3种子模块工作模式，从而控制子模块电容的充放电。子模块电压值在额定值附近波动，上、下桥臂子模块的导通个数决定上、下桥臂电压以及MMC的交流侧输出电压，通过控制上、下桥臂子模块导通个数之和始终为n，以维持直流侧电压Udc的稳定。

1.2 传统均压策略

子模块较多时，传统MMC采用NLM技术与冒泡排序算法相结合的均压策略。该策略首先根据桥臂电压参考值，计算出上、下桥臂应投入的子模块数Nref；再将桥臂全部子模块电压进行冒泡排序，若桥臂电流大于0，则投入电压最小的Nref个子模块进行充电，若桥臂电流小于0，则投入电压最大的Nref个子模块进行放电。根据NLM技术，上、下桥臂应投入的子模块个数为

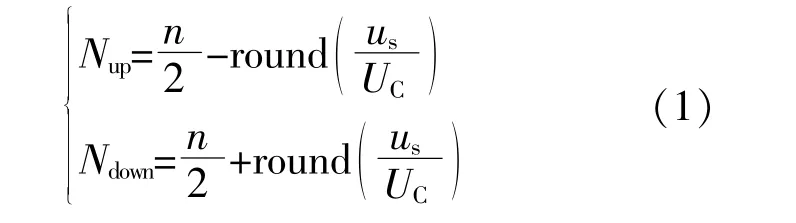
式中：Nup，Ndown分别为上下桥臂应投入的子模块数；n为单个桥臂的子模块总数；round为取整函数；us为换流器阀基控制器得到的调制波电压；UC为子模块电压参考值。

实际工程中，时间复杂度是影响系统运行效率 的 关 键 因 素，常 用O[f（n）]表 述，f（n）为 与 最 坏情况复杂度T（n）同数量级的辅助函数。当桥臂子模块数为n时，使用冒泡排序算法的排序次数为

式中：T（n）为情况最差时冒泡排序的排序次数。

当桥臂子模块个数增加时，排序次数呈指数倍增长，且每一控制周期都将所有子模块的电压排序，提高开关器件的投切频率，增大系统损耗。

2 改进电容均压策略

2.1 希尔排序原理

希尔排序算法原理是先设置一个小于序列个数n的增量d，所有距离为增量倍数的分为一组，每组使用插入排序算法排序，排序后继续缩小增量分组，重复分组和插入排序步骤直至增量为1，即可得到有序数列。希尔排序实现了相距较远元素的比较，一次比较可能使元素朝最终位置前进一大步，消除了元素的多次交换。当增量取值为2k-1（k∈Z）时，其 时 间 复 杂 度 能 够 达 到O（n1.5）[15]。

2.2 改进电容均压算法的实现

传统电容均压策略根据桥臂投入子模块数的增减和电流方向，将桥臂分为6种工作状态，如表1所示。

表1 现有均压策略桥臂的工作状态Table 1 Operating status of the bridge arm of the existing voltage equalization strategy

MMC稳态运行时，设控制器的控制周期为Tc，调制波电压增量为

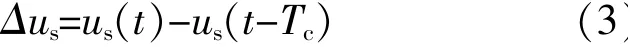
式 中：us（t）为t时 刻 的 桥 臂 调 制 波 电 压。

由 式（1）可 知，当 Δus＞0，则 上 桥 臂 投 入 子 模块参考值Nup与上一控制周期相比减少或不变，反之Nup增加或不变。本文根据桥臂电流的方向和每一阶段 Δus的正、负，将桥臂的工作模式分为4种工作状态进行控制，如表2所示。

表2 改进电容均压策略桥臂的工作状态Table 2 Operating status of the bridge arm with improved capacitor voltage equalization strategy

在理想情况下，子模块电容参数、开关器件的漏电流及电容放电电阻相同，如果投入组与切除组子模块个数不变，在电容充、放电后的组内电压大小顺序将不变。但实际工程中，以上子模块参数很难保证一致[16]。切除组的子模块电容电压大小顺序不变，投入组的顺序受子模块电容大小不一致的影响，会出现个别顺序的改变。若采用插入排序对其简单微调，即可使投入组有序。另外，根据文献[16]，对于投入组的插入排序还可做限制步数的进一步优化。

为降低开关频率，交换投入组与切除组个别子模块的状态，使上一控制周期的投切状态的改变尽量少。根据Nref增加、减少投入子模块数对投入组的有序性也无影响，而子模块状态的交换将会使投入组与切除组无序，因此每一控制周期都须要对组内电压进行排序。通过上述子模块电压变化规律分析可知，Δus＞0（即桥臂投入子模块增加或不变），若切除组已有序，则不须要进行组内排序即可投入新的子模块；Δus＜0时，若投入组已有序，将同样不须要进行组内排序即可进行切除子模块操作。基于此，个别子模块投切状态的交换若能以维持投入组或切除组的有序性为条件，可使各桥臂工作状态下一控制周期子模块投切状态的变动不再排序。

改进电容均压策略将桥臂子模块分为投入组和切除组，根据NLM计算出所需投入子模块数Nref，投入组序列始终放置切除组序列之前。桥臂状态改变后的第一个控制周期子模块电压序列有序性较差，且控制方式须要改变，此控制周期对全部子模块电压希尔排序。对于子模块电压的排序须要将子模块电压存入数组中并编号，本文称此数组为电压储存数组。为了便于叙述，引入指针P，每个控制周期开始时P=0，文中ui为电压储存数组下标为i的子模块电压，m为上一控制周期桥臂所需投入子模块数。以上桥臂为例，算法在每种桥臂工作状态下的详细步骤如下。

状 态1：桥 臂 电 流＞0且-Δus＞0，第 一 个 控 制 周期对所有子模块电压希尔排序为升序，须要维持此工作状态下切除组的有序性。由于投入组子模块充电，除第一个控制周期外，其余每个控制周期以切除组最后一位电压值un+P加一定值作为投入组电压上限Uou，此定值为子模块状态交换偏差值Ue。上一控制周期的投入组子模块电压ui（i∈[1，m]）依次与此上限值比较，若越限则与切除组子模块电压最小值uNref+1+P（即切除组第一位）交换，并将交换至切除组的越限子模块电压放置切除组序列最后一位，指针P加1后更新投入组电压上限（Uou=un+P+Ue），投入组下一位子模块电压与新的切除组上限值进行比较。若没有越限则直接进行投入组下一位的比较，直至第m位比较完成，子模块的状态交换过程结束。

状 态2：桥 臂 电 流＜0且-Δus＞0，与 状 态1的 步骤类似，所不同的是第一个控制周期对所有子模块电压希尔降序排列，设置投入组电压下限Uol=un+P-Ue。

模 式3：桥 臂 电 流＞0且-Δus＜0，第 一 个 控 制 周期对所有子模块电压希尔升序排列，为维持投入组的有序性，其余各控制周期开始时先对投入组进行限制步数的插入排序，再以投入组第一位电压值un+1-P减Ue作为切除组电压下限Ufl，上一控制周期的切除组子模块电压ui（i∈[n+1+m，2n]）依次与此下限值比较，若越限则与投入组子模块电压最大值un+Nref-P（即投入组最后一位）交换，并将交换至投入组的越限子模块电压放置投入组序列第一位。指针P加1后更新切除组电压下限（Ufl=un+1-P-Ue），切除组下一位子模块电压与新的下限值进行比较。若没有越限则直接进行切除组下一位的比较，直至切除组最后一位比较完成。

状 态4：桥 臂 电 流＜0且-Δus＜0，与 状 态3的 步骤类似，不同之处在于第一个控制周期对所有子模块电压希尔降序排列，设置切除组电压上限Ufu=un+1-P+Ue，此处不再赘述。

桥 臂 工 作 状 态1，2，3，4的 子 模 块 状 态 交 换如图2所示，图中深色部分框图表示电压越不同限值的子模块电压。

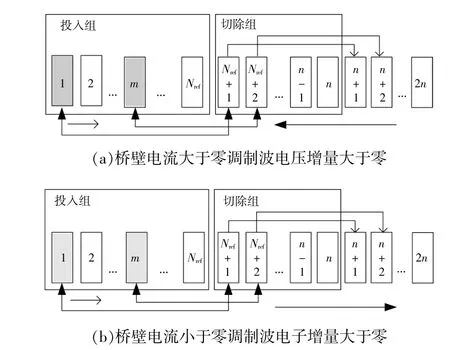
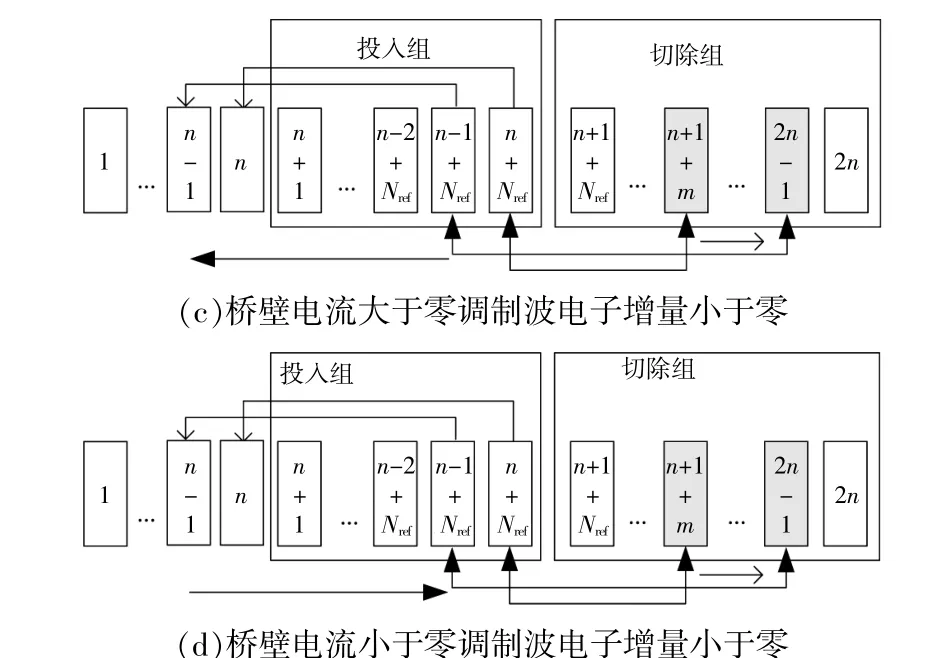
图2 各工作状态下子模块状态交换示意图Fig.2 Schematic diagram of state exchange of submodules in each working state

由图2可知，本文所提算法将电压储存数组的数量增大至2n，可根据指针P的最大值做相应减小。子模块进行一次移位即维持投入组或切除组电压序列的有序性，增大了算法的空间复杂度而减小了算法时间复杂度。

改进电容均压算法的流程如图3所示。

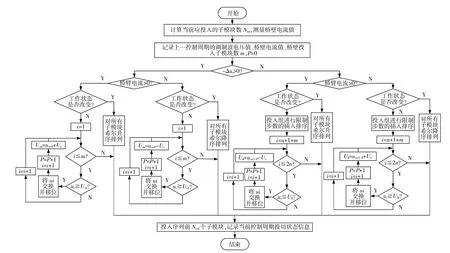
图3 算法流程图Fig.3 Algorithm flowchart

3 仿真验证

在PSCAD/EMTDC环境下搭建了单端逆变侧MMC模型，分别与传统冒泡排序算法、文献[11]的均压算法仿真比较，逆变侧换流器采用电压外环和电流内环的双闭环控制，仿真模型主要参数如表3所示。

氩弧焊打底加手弧焊填充盖面的焊接工艺，经过各专业公司多年的理论指导和实践研发已经能够熟练掌握，合格率高，焊接设备简单，相对于现场的施工条件能够更好的接受和使用。不过对于一些返修无法进行背面充气保护的位置，就增大了氩弧焊焊接工艺的难度和易出现缺陷的几率。对此为了能够更好地适应现场焊接环境的多变性和不可确定性，提出使用焊条电弧焊打底的焊接工艺，并进行试验。

表3 仿真模型参数Table 3 Simulation model parameters

3.1 算法时间复杂度

本文从单位时间比较次数、离线仿真时间两方面与传统冒泡排序算法进行比较。本文所提均压算法在多数控制周期并不排序[14]，或只对投入组进行限制步数的插入排序，故以单位时间内算法进行的总比较次数作为时间复杂度衡量指标，计算了两种算法在不同桥臂子模块数下1 s内的总比较次数。控制周期为20μs，仿真时长为5 s，本文所提算法子模块状态交换偏差值取0，插入排序的限制步数取Nref/3，两种算法的单位时间比较次数和仿真耗时如表4所示。

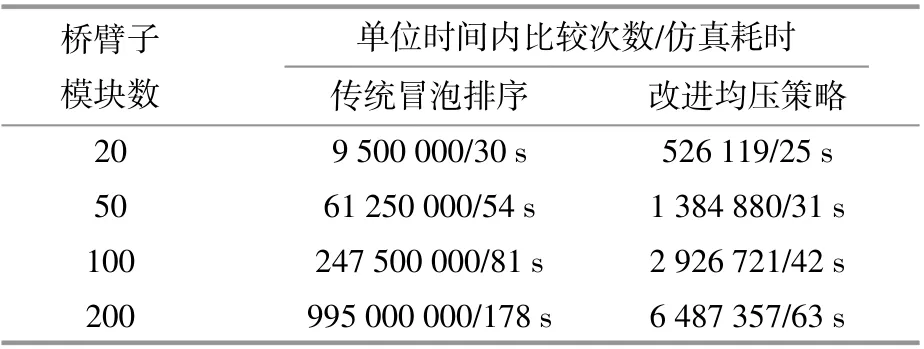
表4 单位时间比较次数与仿真耗时Table 4 Comparison times per unit time and simulation time

由表4可知，随着桥臂子模块数的增大，本文所提算法单位时间所需的比较次数远小于冒泡排序，桥臂子模块数由20增加至100时，比较次数增加至原来的26.05倍。当桥臂子模块数增至200时，比较次数增至原来的104.74倍，增幅符合O（n2）的关系，而改进控制算法比较次数是原来的5.56倍和12.33倍，比较次数增涨较为缓慢且呈线性O（n）阶。在21～201电平时，比较次数与数据规 模 的 关 系 为T（n）≈1.1n，这 低 于 文 献[18]所 提均压算法的1.45n和文献[5]线性时间选择算法的1.9 n。随着模块数的增加，改进均压算法相比冒泡排序算法仿真时间明显缩短，模块数为200时，改进均压算法的仿真时间约为传统冒泡排序算法的1/3，表明本文所提算法能够显著提升系统的运行效率。

3.2 电容均压效果

从电压波动、平均开关频率两方面与设置组间最大允许偏差值的均压算法进行比较分析。桥臂子模块数量为20，控制周期为20μs时，本文所提算法Ue取1，5 V与文献[11]所提算法组间最大偏差值取30 V的子模块与电压仿真波形如图4所示。

图4 桥臂子模块电压仿真波形Fig.4 Bridge arm submodule voltage simulation waveform

平均开关频率定义为[19]

式中：nswitch为单位时间内一个桥臂所有子模块的开关次数总和；n为桥臂子模块总数。

子模块投入触发值为1，切除为0，当子模块触发值与上一控制周期触发值的和为1，即子模块的投切状态发生变化，计数器加1，计算子模块单位时间所有子模块的总开关次数nswitch，从而得到平均开关频率。取稳定后2～5 s的子模块电压最大值和最小值，计算电压波动百分比，取3～4 s的总开关次数计算出平均开关频率。

图5为电压波动、平均开关频率随子模块状态交换偏差值Ue取不同值时的变化情况。由图5可以看出，当Ue为0时，电压波动百分比为7.67%，开关频率为3 303.8 Hz。未加入Ue=0时，随着Ue的增大，电压波动百分比增大而平均开关频率下降。因此，在电压波动允许的范围内，选择尽量大的子模块状态交换偏差值，可以有效降低开关频率，同时验证了所提均压算法调节电压波动、开关频率的有效性。

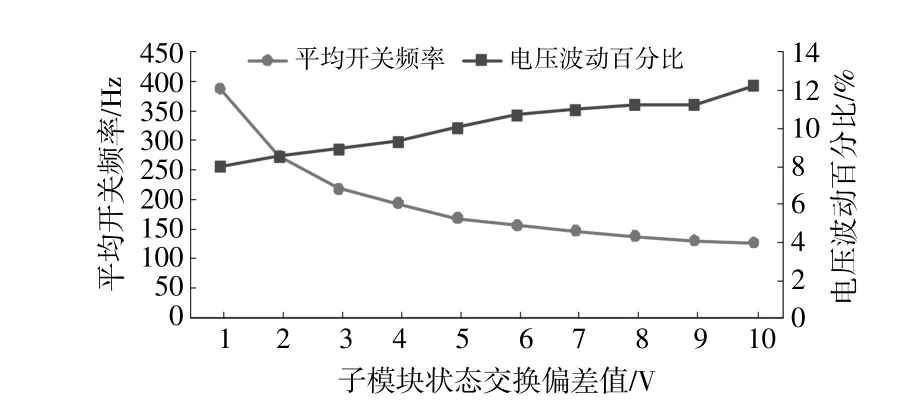
图5 电压波动、平均开关频率与Ue的关系Fig.5 Relationship between voltage fluctuation，average switching frequency and Ue

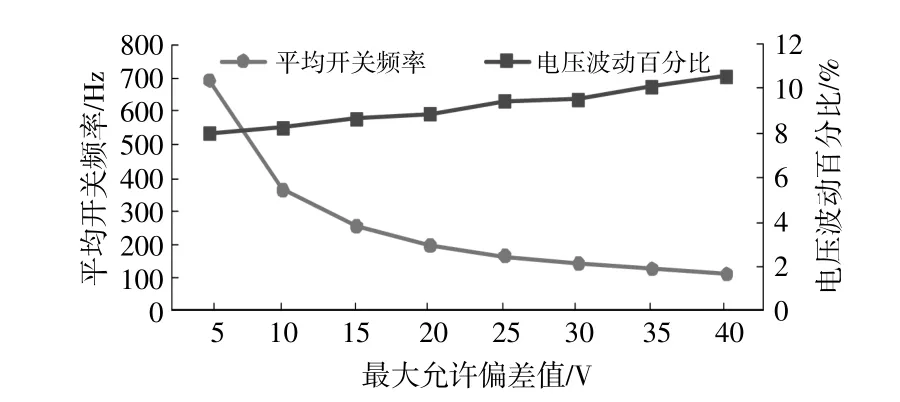
图6 电压波动、平均开关频率与最大允许偏差值的关系Fig.6 Relationship between voltage fluctuation，average switching frequency and maximum allowable deviation

去除此最大允许偏差值下的坐标点，本文算法在Ue为1 V时，与文献[11]所提算法组间最大允许偏差值取5 V时的电压波动百分比相同，约为7.93%，文献[11]的平均开关频率为689.5 Hz，本文算法平均开关频率为387.15 Hz。本文所提算法在Ue为3时的电压波动百分比为8.8%，平均开关频率为218.35 Hz，文献[11]算法在组间最大允许偏差值为17 V时，具有相同电压波动百分比，而平均开关频率为222.55 Hz。可以看出，文献[11]算法的平均开关频率随电压波动的增涨降幅较大，但在电压波动较小时具有较高的开关频率。这表明本文所提算法在电压波动百分比小于约8.8%时，都具有小于文献[11]的平均开关频率。

本文方法在子模块电容电压波动为8.8%的参数下，换流器出口处a相电流谐波总畸变率（THD）如 图7所 示。

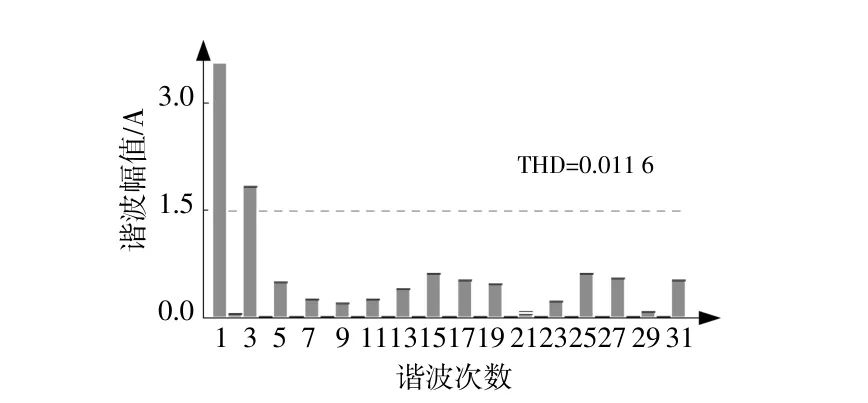
图7 换流器出口处a相电流FFT分析Fig.7 FFT analysis of a-phase current at the outlet of the converter

由图7可知，换流器出口处电流THD为0.011 6，输出谐波含量较少。

4 结论

本文提出一种时间复杂度较低的模块化多电平换流器电容均压算法，通过仿真对比和分析，得出以下结论：①桥臂的工作状态能够以桥臂电流和调制波电压增量的正负分为本文所述的4种状态进行控制；②该算法的时间复杂度较低，通过仿真结果可知，在21～201电平时，平均最大时间复杂度约为1.1n，在降低时间复杂度的同时也降低了开关频率；③本文所提算法设置的子模块状态交换偏差值能够调节电压波动和换流器开关管的开关频率，与增设组间最大偏差值的电容均压算法相比，能够在较低的子模块电压波动下，同时具有较低的器件开关频率。