基于熵值修正G2赋权-Mamdani模糊推理的风电场选址研究

吴梦成，孙 燕，刘 倩

（中国海洋大学 工程学院，山东 青岛 266100）

0 引言

风能是一种清洁可再生能源，风能利用有巨大的发展潜力。风电场选址问题是风力发电的前期工作和首要任务，直接影响风电场的经济效益，对风电的可持续发展具有重要意义[1]。风电场选址须要综合考虑经济、自然等因素，具有复杂性和不确定性。因此，如何对风电场的候选场址进行客观的评估决策逐渐成为研究的热点[2]～[4]。

针对风电场选址问题，文献[1]利用层次分析法（AHP）构建了选址的递阶层次模型，通过评价得分描述了侯选场址的优劣，但这种方法在构造判断矩阵时依赖专家判断，导致结果受主观因素的影响。针对这一不足，文献[2]，[3]在使用AHP时考虑了模糊因素，减少了主观判断引起的影响，但随着决策目标和影响因素数量的增加，计算会变得更加复杂。文献[4]使用模糊TOPSIS和灰色关联度相结合，有效处理多准则问题，但模糊化及去模糊化处理简单，未能良好地体现不确定性。

对于具有多影响因素和决策目标的多准则决策（MCDM）问题，一些学者提出了Mamdani模糊推理方法。模糊推理是一种非线性方法，它使用模糊规则来对人类知识的各个方面进行建模，整合定性和定量因素。该方法可以采用语言变量来处理不精确的信息，由于其灵活和便捷的评估，该方法已广泛应用于复杂的系统和决策过程，例如风险 评 价[5]、安 全 评 价[6]～[8]和 机 械 控 制[9]等，但 很 少 有研究人员使用模糊推理方法来选择风电场址。

鉴于以上分析，风电场选址问题具有系统性，须综合考虑各因素的模糊性。语义等级的划分和评价标准具有不确定性，Mamdani模糊推理方法计算过程简洁，符合人们的逻辑思维，相较于传统MCDM方法，更适宜解决多输入多规则的不确定性问题，但该方法未确定指标权重。为此，本文提出了基于Mamdani模糊推理和修正赋权的方法。首先，通过分析各影响因素，构建风电场选址指标体系；其次，引入专家判断，将主观赋权法-G2法和客观赋权法-熵权法相融合，采用定性定量结合分析，基于熵值修正G2赋权综合确定权重；再次，依据模糊逻辑，通过模糊规则及隶属度函数推理出各准则层模糊推理值，即定义为综合评价值；最后，将综合评价值和权重结合得出候选场址的优劣状况及排序。

1 风电场选址决策模型的建立

1.1 构建风电场选址指标体系

遵循科学性与实用性、特殊性与统一性、主观性与客观性的原则，通过文献分析法和专家调查法选取影响风电场选址的各项因素，建立选址指标 体 系（图1）。

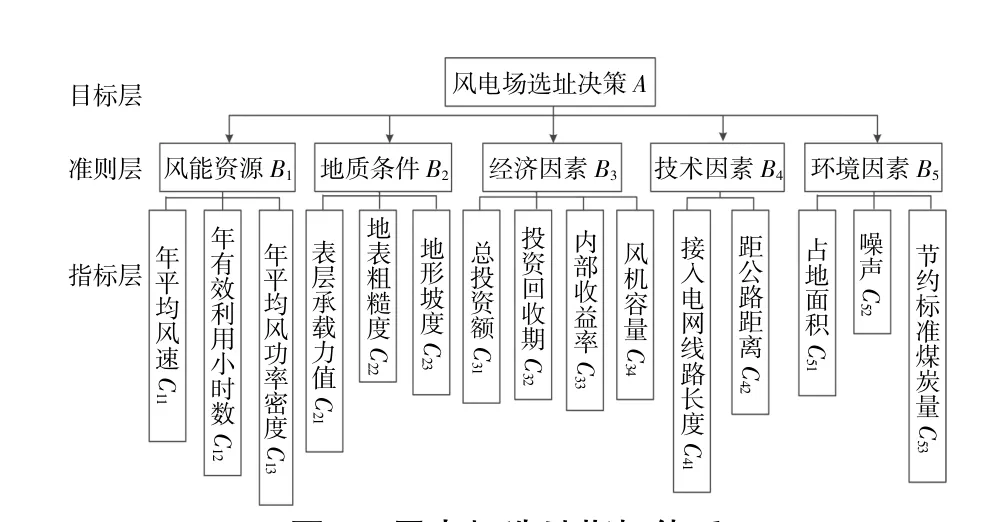
图1 风电场选址指标体系Fig.1 Index system for wind farm site selection

1.2 基于Mamdani算法的模糊推理系统

模糊推理用语言变量来表达专家知识，通过条件语句来描述变量间的关系，其中Mamdani型模糊推理系统是最常见的推理算法[10]。

1.2.1 语言变量及隶属度函数

在综合评价的过程中，为便于模糊规则的建立，须要将准则层的各输入变量及输出变量划分为若干等级。考虑到风电场选址决策各指标的不同要求，通常选用连续型隶属度函数。其中标准三角函数和高斯函数的表达式分别为

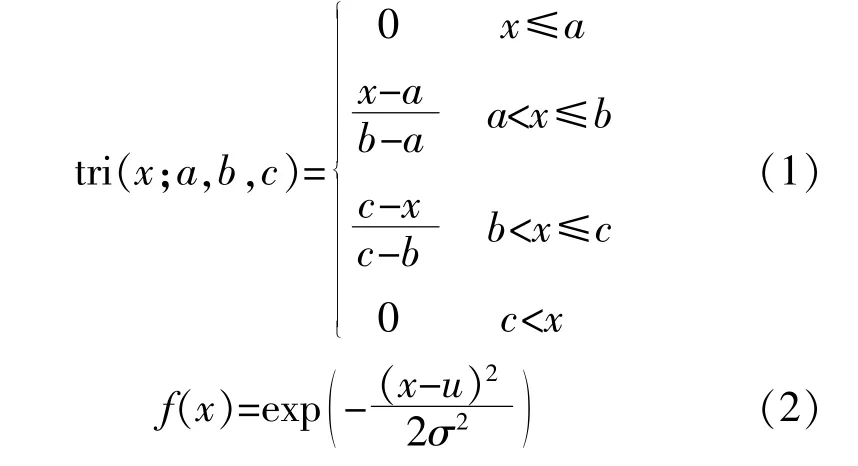
式中：a，b，c均为定义在相应数值区间上划分的间隔；u为高斯曲线的中心，决定了函数的平均水平；σ为影响曲线的陡峭程度，σ越小，曲线越陡。

1.2.2 Mamdani型模糊推理

模糊规则库是模糊推理系统的核心部分，一般MCDM问题均需以多前件多规则为前提，其逻辑示意如下：

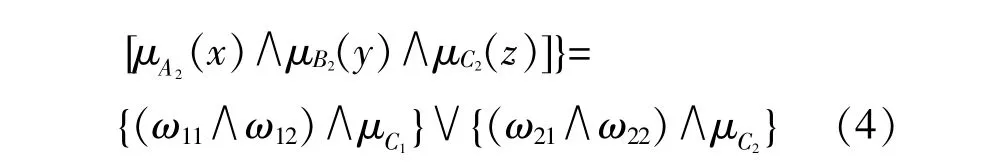
式中：C′为最终模糊化后的模糊集；∧为取小蕴涵算 子；（ω1∧ω2）为 刻 画 了 模 糊 集 合A与A′，B与B′之间的贴近度。

贴近度越大则结论模糊化程度越高，其反映在图像上为交集取小部分，该方法被形象称为Mamdani推理削顶法[7]，如图2所示。

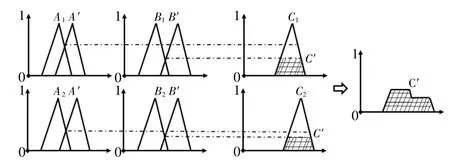
图2 Mamdani推理削顶法Fig.2 Mamdani reasoning method

1.2.3 去模糊化

重心法是最常见的去模糊化方法，取隶属度函数曲线与横坐标围成面积的重心为模糊推理最终的输出精确值，其具有更平滑的输出。重心法计算式为

式中：G*为输出模糊集C′的重心值；g为输出变量。

1.3 修正赋权确定指标权重

本文依据一种新的熵值修正G2赋权方法，该方法能够同时利用指标熵值与专家经验得到指标间相对重要程度的刻画，减少了G2法受主观因素影响较大和熵值法受数据变异程度影响较大的劣势，使赋权过程综合主客观两方面的有效信息，兼具两种赋权法的优点，还规避了组合权重如何分配的难题[11]。

通过对m个评价指标和n个评价对象的原始数据矩阵规范化和无导向化，定义第i个指标的熵值为

2 实例分析

本文对广东省茂名市电白区放鸡岛岛屿进行风电场宏观选址决策，通过排除不适宜区域（生态保护区和旅游开发区），在风资源丰富区域预先选取了6个候选场址。通过搜集历史风速资料、远景GREENWICH风电场设计平台、实地调研等渠道获取了上述方案各评价指标客观数值。

2.1 熵值修正G2赋权

引入专家判断，决策组成员由1位教授兼风能专家、2位副教授和2位高级工程师构成。由专家从评价指标集中挑选出最不重要的元素xim，将其作为唯一参照物，如准则层的B2，指标C12等，将其放置最底层再重新排序。

通 过 式（6）～（8）得 到 最 终 的 修 正 准 则 层 权 重（表1）。

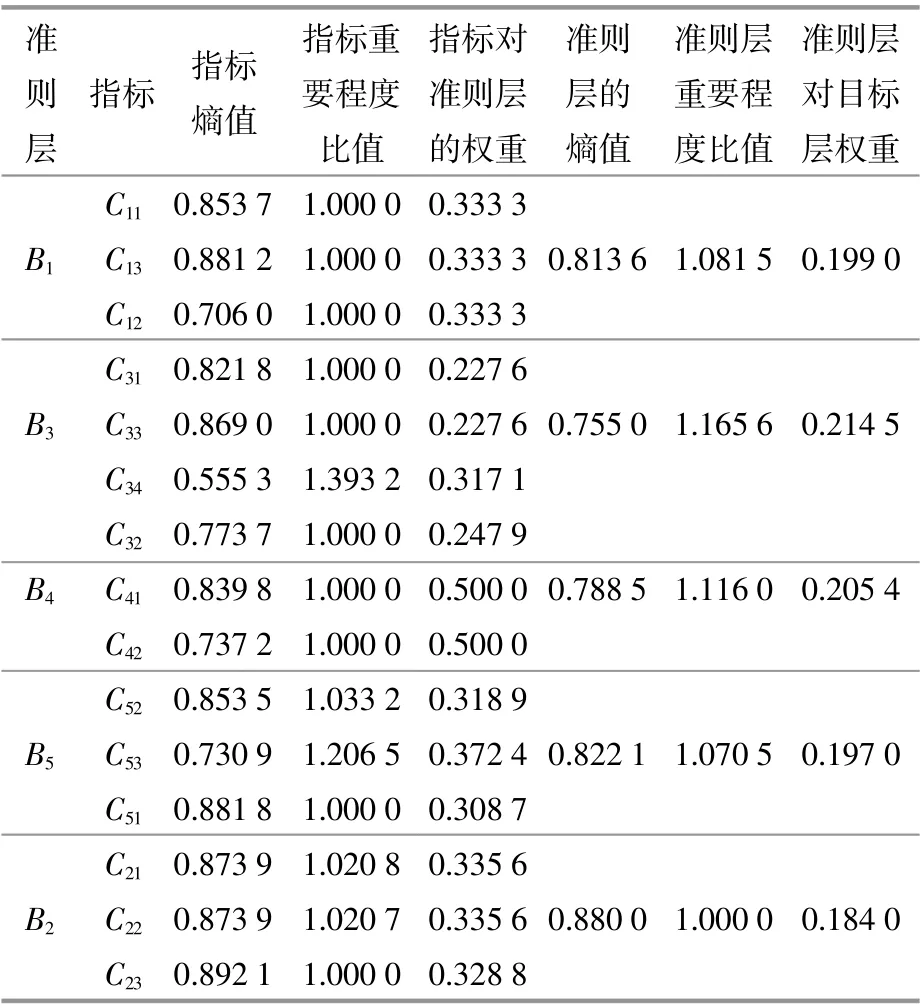
表1 指标熵值及修正权重列表Table 1 List of index entropy and correction weight

2.2 Mamdani模糊推理过程

将6个候选场址的指标层模糊化处理，采用标准三角形、高斯、梯形隶属度函数分布，语言变量 设 置 为5等 级{极 低（VL）、低（L）、中 等（M）、高（H）、极 高（VH）}，经 计 算 可 得 所 有 影 响 因 素 的 模糊化分布。B1的模糊化分布和解释见表2。

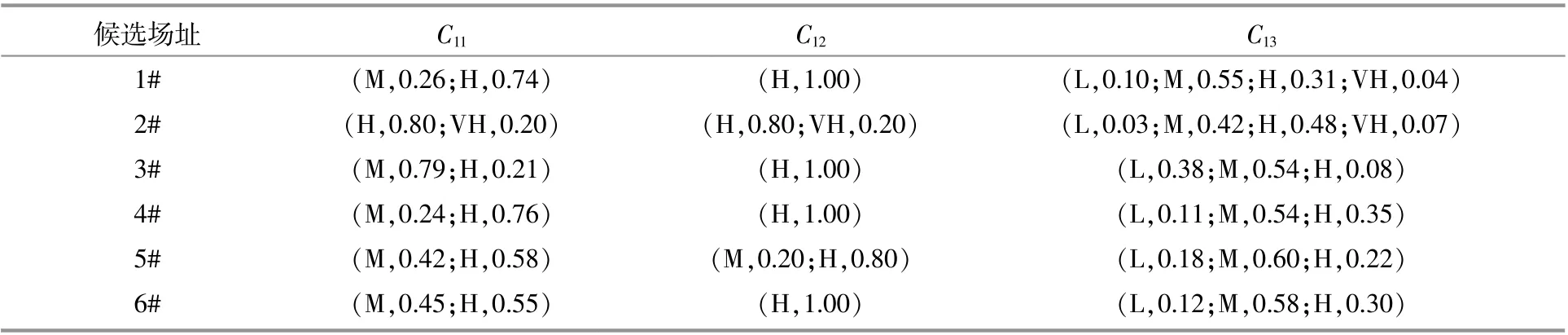
表2 风能资源影响因素的模糊化分布Table 2 Fuzzy distribution of factors affecting wind energy resources

由于本文选取的指标层均为定量数据，属于输入变量，须定义在相应的数值区间内。图3为输入输出变量的隶属度函数图像。

图3中隶属度大小分析如下。

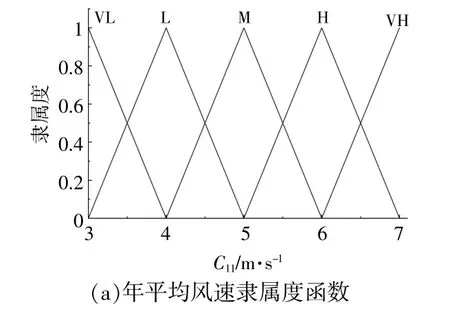
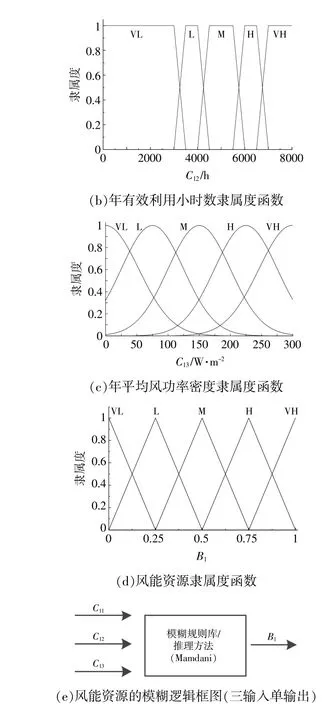
图3 输入输出变量的隶属度函数及推理逻辑Fig.3 Membership function of input and output variables and reasoning logic

①C11

风能资源B1各项数据于测风塔80 m处采集，由于C11较为稳定，采用标准三角形隶属度函数。从实地调查数据来看，其论域定义在[3，7]m/s。其中，1#场址指标C11属于H的模糊隶属度为（5.74-5）/（6-5）=0.74，属 于M的 模 糊 隶 属 度 为（6-5.74）/（6-5）=0.26，其 他 类 似。

②C12

通过相同的调查，C12指标具有相似的属性区间，采用梯形隶属度函数来平滑过渡。其论域定义在[0，8 000]h，区域年平均风力持续时间集中在6 000 h左右。

③C13

通过相同的调查，对风功率密度采用高斯型隶属度函数，此类正态分布图像可以灵活地反映系统的复杂性和非线性。隶属度函数的参数分别设 置 为[50 0]，[50 75]，[50 150]，[50 225]和[50 300]，其论域定义在[0，300]W/m2。采用单值模糊化的方式得出相对于各等级的隶属度大小，再将其标准化。

④B1风能资源

输出结果属于定性评判，采用5等级的标准三角形隶属度函数，定义在区间[0，1]，数值越大，表明选址结果越优。

借助Matlab软件的模糊控制工具箱，推理出各准则层的综合评价值。本文选取风能资源B1的模糊推理过程叙述。通过表2的模糊化分布，建立三输入单输出（5×5×5=125种）的模糊推理系统，逻辑流程见图3（e）。建立起风能资源评价“If-Then”规则库如下，其中每条规则的权重相同。

图4为候选场址1#的风能资源部分“If-Then”规则推理过程，可得1#的B1模糊推理值WER为0.607，处于M和H之间。

图4 风能资源（WER）的模糊推理过程Fig.4 Fuzzy reasoning process of wind energy resources

图5为风能资源的模糊推理控制面。图5说明了输入和输出之间的关系和交互作用，可知指标C11，C12和C13皆与准则 层B1成 正比，且C11影响最大。

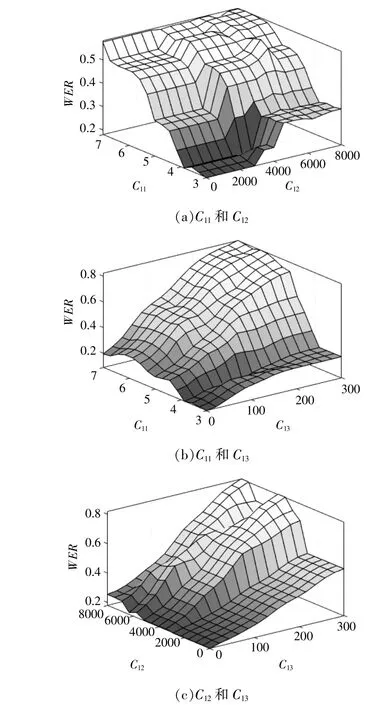
图5 风能资源（WER）的模糊推理控制面Fig.5 Control surfaces of wind energy resources

2.3 结果分析

综上可得所有候选场址准则层的模糊推理值，即定义为综合评价值，结果如表3所示。

由表3可知：1#场址各方面条件均衡；2#场址的风能资源丰富，地质条件较好，经济效益最佳，但与电网距离较远，对环境影响较大；3#场址地质条件相对较差；4#，5#和6#场址各方面条件均比较优秀，难以抉择。故需结合准则层权重加以评价。

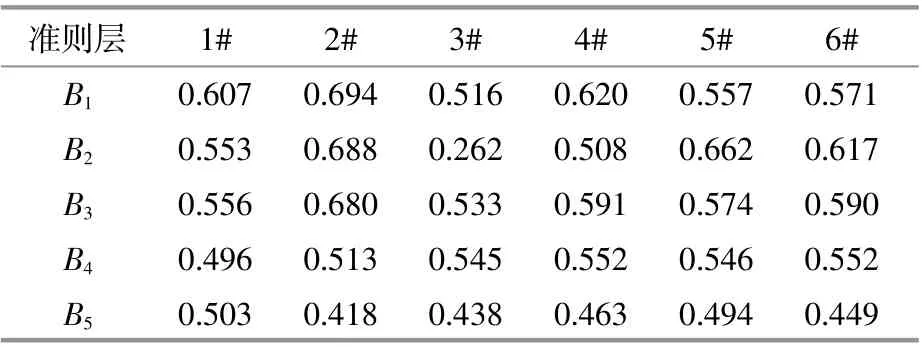
表3 候选场址综合评价值Table 3 Comprehensive evaluation value of candidate sites

通过与熵值修正G2赋权权重{wb=0.199 0，0.184 0，0.214 5，0.205 4，0.197 0}复 合，得 到 赋 权得分和候选区域排序，其值越大，表明选址方案越优。最终得出2#场址的综合评价结果最优，为最佳 候 选 区 域，且 方 案 排 序 为2#＞5#＞6#＞4#＞1#＞3#，说明专家在选址时更注重蕴藏的风能资源和经济效益。

2.4 比较分析与灵敏度分析

将本文排序结果与模糊综合评价法和TOPSIS方法相比较，结果见表4。3种方法所求最佳和最差场址的排名一致，进而验证了本文方法的可行性。

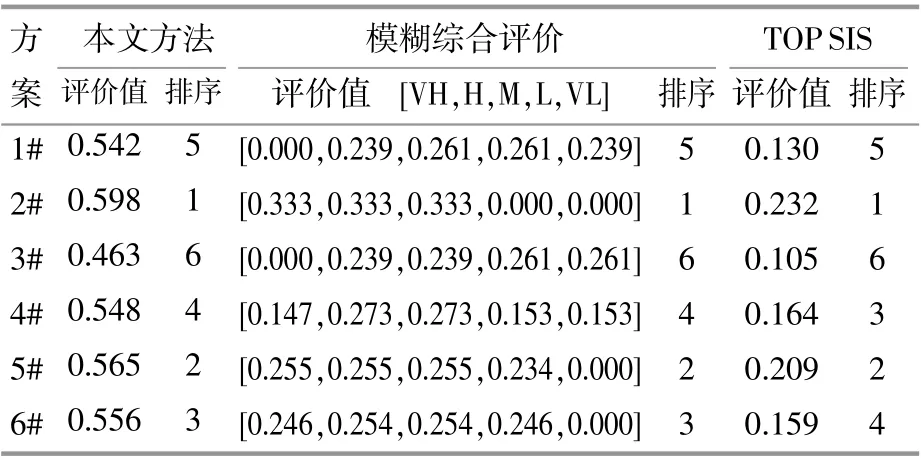
表4 比较分析结果Table 4 Comparative analysis results

根据决策者的偏好对指标权重进行灵敏度分析（图6），以检查态度变化会在多大程度上影响排序顺序并了解决策结果的稳健性。

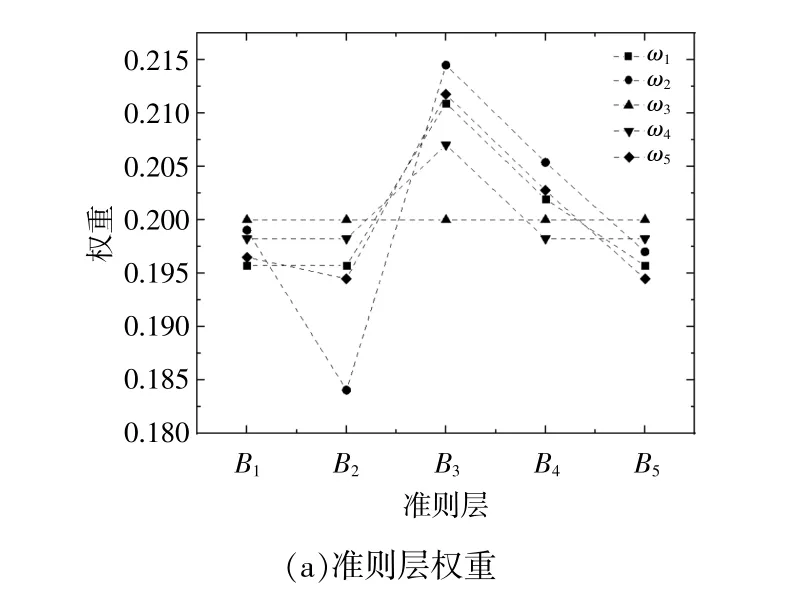
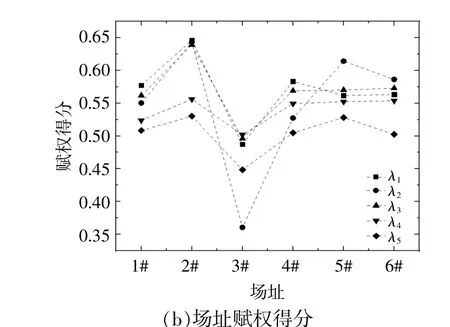
图6 灵敏度分析Fig.6 Sensitivity analysis

前述研究中运用了熵值修正G2赋权，将准则层的B2作为最不重要的元素放置底层再重新排序。现由专家分别将其余准则层作为最不重要元 素，得 到 权 重 如 图6（a）所 示，其 中wj（j=1，2，3，4，5）为5次不同的评判，发现权重大小集中在0.18～0.22，较为稳定。其本质是因为熵值修正G2赋权综合考虑了主观和客观因素，且客观数据相差不大，修正后的权重所受影响较小。

场址赋权得分的灵敏度分析如图6（b）所示，令 λi=0.6（i=1，2，3，4，5）为 分 别 考 虑 不 同 准 则 层为最重要的图像，其余权重认定为0.1，如将B1准则层看作为最重要时，令wB赋权为{0.6，0.1，0.1，0.1，0.1}。从分析结果可以看出，随着专家态度的变化，场址4#，5#和6#排序有所变动，但最佳和最差场址的排名没有改变。这证明了本文所使用方法得到的排序结果是可靠和稳定的，受权重变化的影响较小，提高了决策结果的有效性。其本质是在模糊推理过程中，已经考虑了影响因素的重要性和相关性。

3 结论与建议

①针对风电场实际情况，本文建立了选址评价体系，运用Mamdani型模糊推理得出准则层的综合评价值，考虑了各因素的模糊性，采用“If-Then”推理法则，避免复杂的数学公式推导，利用Matlab工具箱，使评价过程方便快捷。

②采用熵值修正G2的方式分配权重，综合专家的主观信息与数据的客观信息，使赋权更贴合实际。实例表明，文中建立的评价方法有效，提高了选址的可靠性和适用性。

③对于隶属度函数的确定和模糊规则的最优数量，尚无明确的规定，一般通过综合考虑原始数据和专家经验来确定。可以通过构建神经网络，从案例中学习不断调整权重，达到不断完善模型的效果。