基于致动线和大涡模拟的不同入流风况下的风力机尾流特性研究

2021-10-28陈安新

可再生能源 2021年10期

陈安新，孙锐，王凯，许昌

（1.山东电力工程咨询院有限公司，山东济南 250013；2.河海大学能源与电气学院，江苏南京 211100）

0 引言

随着计算机技术的发展，CFD方法在风电场空气动力场的计算中得到了广泛应用。在动量方程中添加源项，利用致动类方法模拟风力机叶片对气流的阻碍作用时，不需要建立实体网格，降低了网格划分难度并提高了计算速度。致动线模型将体积力分布于叶片轴线上，由于考虑了体积力沿叶片展向和旋转方位角的变化，从而更容易捕捉到风力机非定常流动时的尾流特性，尤其是叶尖涡和叶根涡的发展变化[1]。文献[2]～[4]采用AL/NS-LES耦合模型对MEXICO实验风力机进行了数值模拟研究，该模型能够较好地预测MEXICO风力机尾流的扩散、涡核半径、环量以及轴向和切向速度分布。朱翀[5]以NH1500叶片为研究对象，采用k-ωSST湍流模型，从叶片载荷分布和功率系数两个方面比较了致动线方法、叶素动量理论、直接模拟以及风洞试验，验证了致动线方法用于风力机气动数值模拟的可行性。Qian Yaoru[6]采用ALM-LES方法证明了致动线模型在风力机尾流模拟中能够提供准确的载荷预测和高精度的湍流流动。Sarlak H[7]研究了在致动线模型中叶素长度、体积力分布尺度、雷诺数以及亚格子尺度模型对于流动结构和风力机载荷的影响，相比于叶素长度和体积力分布尺度，亚格子尺度模型对于尾流和功率预测的影响较小。卞凤娇[8]在OpenFOAM平台上对比了PISO求解的致动线模型和多重参考稳态求解的CFD实体模型，进而采用致动线模型数值研究了NREL 5 MW风力机在均匀来流中的尾流场特性，包括涡结构、尾流速度亏损、拟涡能等，验证了致动线模型的准确性。

在致动线模型的研究中，对风力机致动线模型进行叶尖、叶根损失修正和三维延迟失速修正的研究较少，也未考虑机舱和塔筒对风力机尾流的影响。本文建立修正后的风力机致动线模型，结合大涡模拟方法，以NREL 5 MW风力机为研究对象，建立包含叶片、机舱和塔筒在内的全尺寸风力机致动线源项模型，研究风力机尾流在不同入流风况下的尾流特性，为风电场微观选址、风力机尾流控制策略等提供理论支持。

1 数学模型

1.1 风力机致动线模型

致动线模型是利用分布在叶片上的体积力模拟叶片对气流的作用，其中叶片体积力利用叶素理论（BEM）计算确定。

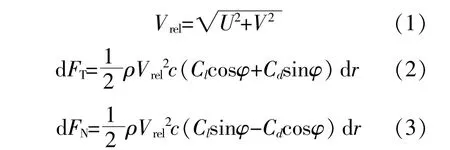
式中：U为来流风速；V，Vrel分别为叶素上气流的切速度和相对风速；FT，FN分别为叶素受到的轴向力和切向力；ρ为空气密度；c为叶素弦长；Cl，Cd分别为叶素的升力系数和阻力系数；φ为入流角，是Vrel与风轮旋转平面的夹角。

采用Shen叶尖、叶根损失修正模型对叶尖、叶根损失进行修正，引入修正系数F1对升、阻力系数进行修正。

1.2 大涡模拟方法

大涡模拟采用滤波函数对连续性方程和N-S方程进行滤波处理，将尺度小的亚格子涡过滤，并在方程中引入亚格子应力项以考虑亚格子涡对大涡运动的影响，而对于网格尺度大的大涡运动，可通过瞬时N-S方程直接求解得到。

对于不可压缩流动，滤波后N-S方程为

2 模型可靠性验证

本文选取风洞试验风力机G1作为致动线模型数值模拟验证的研究对象。R为0.55 m，叶片选用RG14翼型，塔筒高度为0.8 m，额定转速为850 r/min。

计算域长、宽、高分别为30R，6R和6R，其中对转子平面所在的区域进行加密处理（图1），加密区网格单元边长为0.025 m，加密区以外的网格单元按照一定的比例逐渐向外拉伸。整个计算域总网格单元数为1 760 248个，均为六面体结构化网格。入口边界给定恒定的x正方向入流速度U0为5.0 m/s，湍流强度TI为5.5%，出口边界设置为压力出口，上下和左右边界设置为对称边界。

图1 计算域网格划分Fig.1 Grid division in calculation domain

为了研究大涡模拟中亚格子尺度模型对风力机致动线模型数值计算的影响，分别研究SM模型、WMLES模型、KET模型以及WALE模型对均匀入流风速为5.0 m/s下的G1实验风力机尾流流场的影响和对比分析。

图2所示为不同亚格子尺度模型计算得到的风力机旋转平面前1D和尾流区不同位置（-1D，2D，3D，4D，6D和9D）风力机轮毂高度处水平方向轴向速度轮廓线与实验值的对比情况。由图可知，不同亚格子模型的计算结果差别很小，且与实验值吻合度较高，其中图2（d），（f）中SM模型和KET模型的计算结果与实验值相差较小，计算精度相对较好。本文后续将采用SM模型作为大涡模拟的亚格子尺度模型。

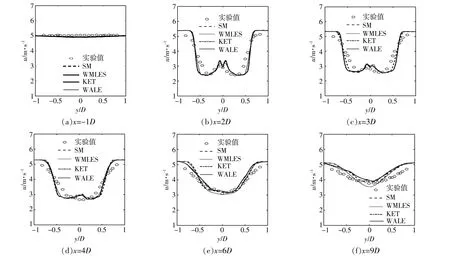
图2 尾流区不同位置轮毂中心水平方向轴向速度廓线Fig.2 The axial velocity profiles in the horizontal direction of the hub center

3 不同入流工况下风力机尾流特性

以NREL 5 MW风力机作为数值计算对象，研究其在不同入流工况下的单台风力机的尾流特性和影响机理。NREL 5 MW风力机R为61.5 m，额定转速为12.1 r/min，塔筒高度为90 m。

计算域示意图如图3所示，设置计算域长、宽、高分别为12D，3D和3D，风轮平面距离入口约为2D。

图3 计算域示意图Fig.3 Schematic diagram of calculation domain

对转子平面所在的区域进行加密处理，风力机位于长、宽、高分别为0.5D，1.5D和1.5D的网格加密区中，加密区网格单元边长为3 m，加密区以外的网格单元按照一定的比例逐渐向外拉伸。整个计算域总网格单元数为4 175 604个，网格均为六面体结构。通过网格无关性验证，网格精度已达到计算要求。计算域的入口设置为速度入口，出口设置为压力出口，左右两面以及顶面设置为对称面，底面设置为无滑移壁面。风力机在额定转速12.1 r/min下运行，计算时间步长设置为0.035 s，整个计算时间持续大约238 s。

3.1 基于不同入流风速的均匀入流风况

在均匀入流条件下，研究工作在相近转速不同叶尖速比状态下的单台风力机的尾流特性。计算时分别取来流风速为3，5，7 m/s和11.4 m/s，对应的叶尖速比分别为15，10，8和7。

图4所示为计算稳定后不同入流风速工况下计算域轮毂中心水平截面的瞬时速度云图。

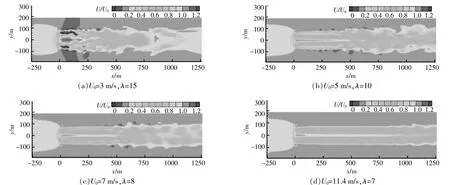
图4 不同叶尖速比工况z=0速度云图Fig.4 Contour of velocity at z=0 under different tip speed ratio conditions

由图4可知：随着入流风速的增大，由风轮阻滞作用造成的尾流长度增加，尾流速度恢复减慢；当轴向入流风速增大时，风力机的相对入流速度增大，从而导致风力机的轴向推力增大，在一定程度上阻碍了气流经过风力机后的恢复能力。从图4（b），（c）可以看出，在离风力机较远的区域，自由流区高速流动的空气在压力的作用下逐渐流向尾流区，引起尾流区和自由流区的空气相互掺混，尾流区的速度开始逐渐恢复，速度亏损逐渐减少，风轮径向方向上的轴向速度梯度逐渐减小。

图5为不同来流风速工况下风力机尾流轮毂中心水平截面的涡量云图和三维涡量（Velocity Invariant Q，Q=0.000 5）等值面图。

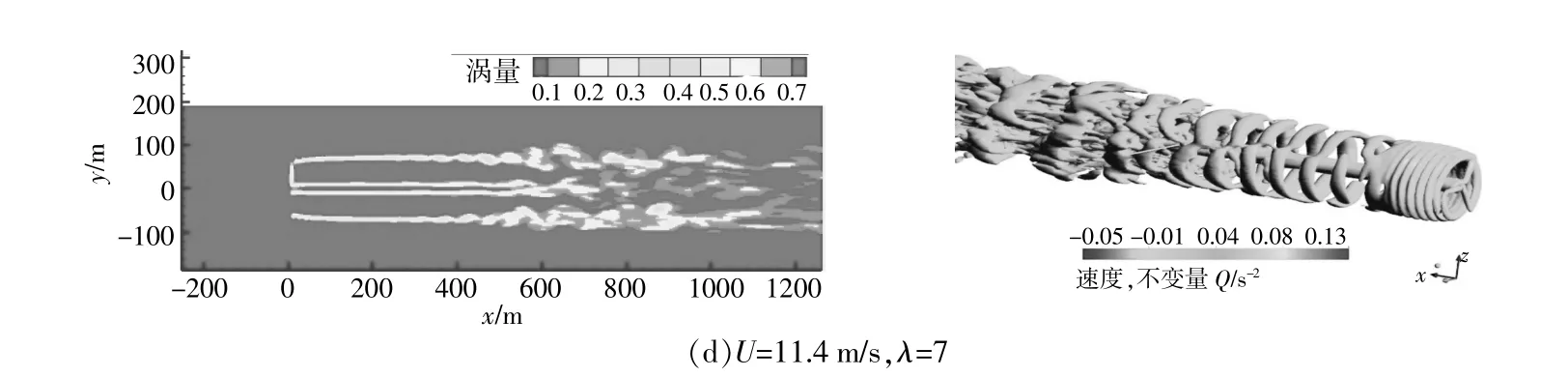
图5 风力机二维涡量云图和三维涡量等值面图Fig.5 2D vorticity contour and 3D vorticity isosurface of wind turbine

由涡量云图可知：来流经过风力机之后，随着入流风速的增加，风力机尾流涡量耗散速率变慢，且不同叶尖速比工况下尾涡开始发生耗散的位置与图4中的瞬时速度云图中速度开始紊乱的位置是一致的；随着入流风速的增大，螺旋状尾涡的涡间距增大，叶尖涡脱落的耗散速率变慢，尾涡向下游持续发展的距离越远；对于同一入流风速，尤其是入流风速较大工况，风力机尾流向下游发展的过程中，螺旋状尾涡的涡间距逐渐增大，叶尖涡核半径也逐渐增加，导致涡与涡之间的干扰作用更强，更容易引起叶尖涡的破裂、脱落。

3.2 基于不同地表粗糙度的切变入流风况

对进口入流风速采用中性大气边界层对数垂直风速轮廓[9]。

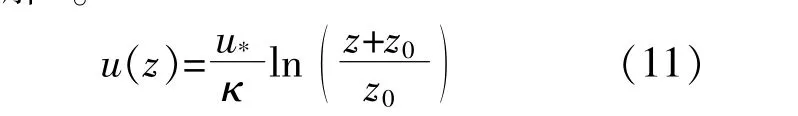
式中：z为离地高度；κ为Von Karman常数，κ=0.418 7；u*为摩擦速度；z0为地表粗糙度长度，共设置4种粗糙度长度，0.001，0.01，0.1和0.7。

设置风力机转速为额定转速12.1 rpm，在轮毂高度处入流风速为额定风速，U（H）=11.4 m/s。

在对风力机致动线模型的研究中，往往忽略了机舱和塔筒对气流的阻碍作用。本文在研究不同地表粗糙度切变大气来流工况风力机尾流特性时，建立了机舱和塔筒的源项模型。

考虑到风力机机舱阻力对来流的影响：

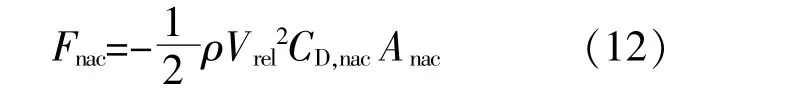
式中：CD，nac为机舱阻力系数，本文取值1.0；Anac为机舱截面积。

参考叶素理论，将风力机塔筒沿塔高方向上同样分成一系列塔筒微元段，每段高度为dh，则任意一个塔筒微元段中心处的气流轴向阻力为

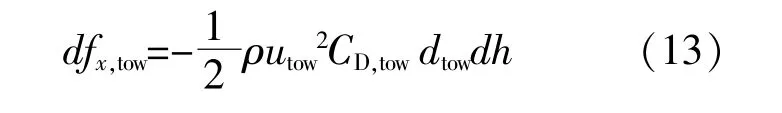
式中：utow为该塔筒微元段中心处来流风速；dtow为该塔筒微元段中心处塔筒直径；CD，tow为塔筒阻力系数，本文取值1.0。

图6为不同地表粗糙度下风力机轮毂中心垂直截面的平均风速云图，图中标尺保持一致。

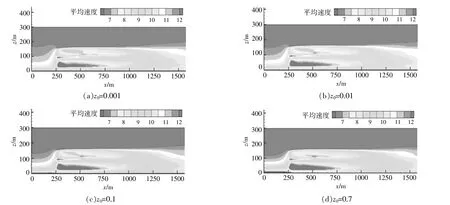
图6 风力机轮毂中心垂直截面平均风速云图Fig.6 Contour of average wind speed in vertical section of wind turbine hub center

由图6可知：受切变来流和塔筒阻力的作用，在离风力机转子平面较近区域，轮毂中心下侧的尾流速度明显低于上侧，而在远尾流区未观察到该现象；不同地表粗糙度下轮毂中心垂直截面平均速度云图差别很小。

图7为不同地表粗糙度下轮毂中心垂直截面涡量云图。

图7 轮毂中心垂直截面涡量云图Fig.7 Contour of vorticity in vertical section of hub center

由图7可知：在考虑风力机塔筒之后，在塔筒后方出现明显的脱落涡，且在下游约1D后消失；不同的地表粗糙度长度引起了涡量云图的细微差别，随着地表粗糙度长度的增加，在塔筒竖直方向内相同高度对应的风速减小，导致塔筒产生的阻力减小，风力机塔筒形成的涡更容易发生脱落和破裂，进而导致脱落涡的涡量值增加。

图8为不同地表粗糙度工况下，风力机各尾流位置轮毂中心处垂直平均风速轮廓线，其中平均风速已做归一化处理，图中点划线所包含的区域代表风轮旋转平面，点线所在高度为轮毂中心高度。

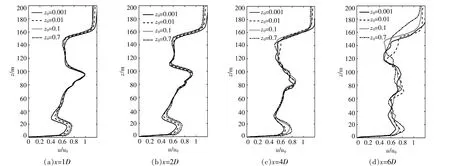
图8 尾流垂直风速廓线Fig.8 Vertical wind speed profile of wake

由8图可知：受到切变来流和塔筒阻力的影响，风力机尾流垂直平均风速廓线呈现不对称性，尤其是在较近尾流区（1～4D）不对称性较为明显；轮毂中心下侧的速度亏损大于上侧，而随着尾流向下游发展，垂直方向上的叶尖涡和塔筒产生的涡系充分掺混，导致在一个风轮高度上平均风速差别较小，表明风力机塔筒的存在增加了尾流区湍动能，从而加速了轮毂中心下侧的尾流速度的恢复。与入口风廓线特征相似的是，随着地表粗糙度长度的增加，较近尾流区中的垂直风廓线轮毂中心高度以下的平均风速减小，而在轮毂中心以上高度的平均风速大小受地表粗糙度长度变化的影响较小，且在远尾流区，整个风轮高度的平均风速开始不受地表粗糙度长度变化的影响。