基于聚类和长短期记忆神经网络的光热电站并网电力预测

余 洋，陈 庚，余佳磊，李连坪，师进文，李明涛

（1.中国平煤神马集团尼龙科技有限公司，河南 平顶山 467000；2.西安交通大学动力工程多相流国家重点实验室国际可再生能源研究中心，陕西 西安 710049）

太阳能光热发电技术清洁高效，易于推广，市场潜力巨大[1]。据中国气象科学研究院数据，中国不同地区每年总太阳能辐射量最低为3 340 MJ/m2，最高为5 852 MJ/m2。丰富的资源保障了中国进行太阳能开发利用的广阔前景。然而，光热发电受天气因素影响具有明显的间歇性和波动性，这种特性在发电系统并网后，会对电网的稳定性带来冲击。对光热电站的并网电量（简称发电量）进行预测，有助于电网提前制定调度计划，有效减轻光热发电并网造成的不利影响[2-4]。

在太阳能电站发电量预测方面，当前国内外研究多聚焦于气象参数的变化预测及发电量与气象参数的联系[5-7]。Voyant 等人[8]将太阳能预测方法分为传统的物理模型预测方法和机器学习预测方法。其中物理模型预测方法包括间接预测天气的外推法[9]以及利用数值天气预报（NWP）[10]进行分析的数值天气预报模型法；机器学习预测方法主要有人工神经网络（ANN）、差分自回归移动平均模型（ARIMA）等[1]时序数据连续预测方法。外推法主要是根据历史数据寻找数据间的联系与规律，包含太阳辐照度的预测、天气的预测等。Yang 等人[11]利用回归模型对光伏发电数据进行统计分析，获得未来1 h 的温度、降水概率和太阳辐照度，最后再运用模糊推理方法对发电量进行精确预测。Cao 等人[12]针对太阳总辐照度的影响因子，利用相关系数法对太阳辐照度影响进行排序得出主要影响因子，再利用折现系数法修正偏差，改进辐照度的预测方法。数值天气模型法是根据数值天气预报的情况，将其直接作为输入参数再结合统计学对发电量进行建模和预测[13-14]。这些方法都是基于太阳能电站的特性以及不同的天气预报变量如水平辐照度、相对湿度、云量[15]等，当天气稳定时，如晴天，其预测性能较高[16]。德国的Lorenz 等人[17]提出利用天气预报的太阳辐照度预报值提前3 天对欧洲国家的光伏电站进行发电量预测，其平均绝对误差百分比在40%以上。

机器学习预测方法主要运用时间序列模型以及早期的神经网络进行预测研究。Kasburg 等人[18]使用循环神经网络（RNN）模型，将其加入太阳能发电的预测中，改变了传统的使用有源太阳能跟踪器提高发电量的方式，该方法具有较好的非线性处理能力，能更好的预测太阳能发电。Ashraf 等人[19]利用ANN 方法对Lakshadweep 群岛上的光伏并网系统进行预测，利用ANN 将太阳能光伏发电输出与太阳辐射、组件温度、清洁度指数等相关参数进行插值，得出3 个相关模型并加以对比，但预测准确度缺乏实际验证，且输入参数的相关性缺乏分析。此外，Diagne 等人[20]对混合模型展开了深入研究，将传统的时间序列模型（如ARIMA 和自回归AR 模型）与气象数据结合，得出一个更加复杂但是更加精确的模型。但是该模型要求输入数据的时间和空间的分辨率极高，并且对计算机的计算能力要求极高，限制了该方法的推广应用。

综上所述，当前太阳能电站发电量预测从传统的物理模型方法发展到现在的机器学习预测方法，其预测精度在不断提升。但在当前的研究中，通常对气象因素的相关性分析比较宽泛，很多工作仅将太阳辐照度、温度作为输入量。此外，大量研究集中于不同预测模型的尝试，而忽略了对数据内在逻辑的挖掘，未能将模型与领域知识深度耦合，限制了其预测精度。

对此，本文以美国加利福尼亚州（简称加州）光热发电系统并网电力预测问题为例，首先研究气象参数与发电量之间的相关性，进而利用近邻传播（AP）聚类算法对比不同发电模式下气象参数对发电影响差异，挖掘数据间的深层联系。然后，基于此建立长短期记忆（LSTM）神经网络基准模型对光热系统发电量进行预测，并根据聚类结果针对性地改进预测模型，以此提高特殊天气条件下的预测精度。

1 数据及处理

1.1 数据描述

本文选取美国加州境内光热电站并网电力总量数据作为研究对象。该数据为加州ISO 项目[21]公开数据，数据时间分辨率为1 h，单位为MW·h。通过美国国家可再生能源实验室（NREL）公开的光热电站数据获得加州的全部14 座光热电站信息。对其运行时间进行梳理，发现从2014年12月1日至2017年1月31日期间既没有新建电站投入运营，也没有已运营电站停止发电，系统运行稳定。因此将该时间段内的发电数据作为本文研究的数据样本。该时间段内共有13 座电站处于发电状态，其中包含solar electric generating station（SEGS）项目的全部9 座电站，电站数据信息见表1[22]。

从表1 电站建设位置来看，SEGS 项目的9 座电站地处2 个不同区域，因此可将其总体看成2 个发电位置，加上其余4 座电站总计可分为6 个不同的发电位置。图1 为美国加州光热电站地理位置。

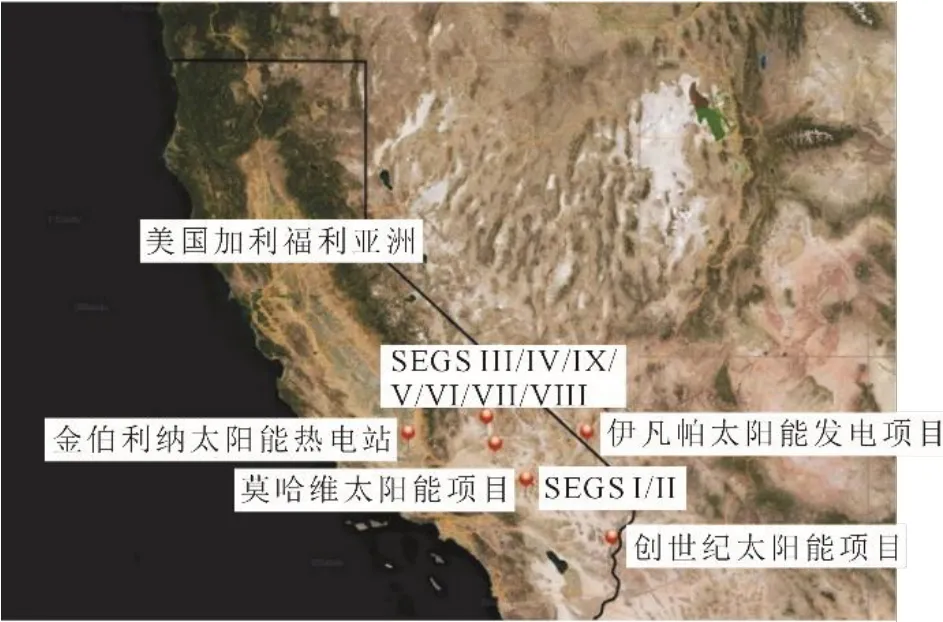
图1 美国加州光热电站地理位置Fig.1 Location of the CSP plants in California,USA

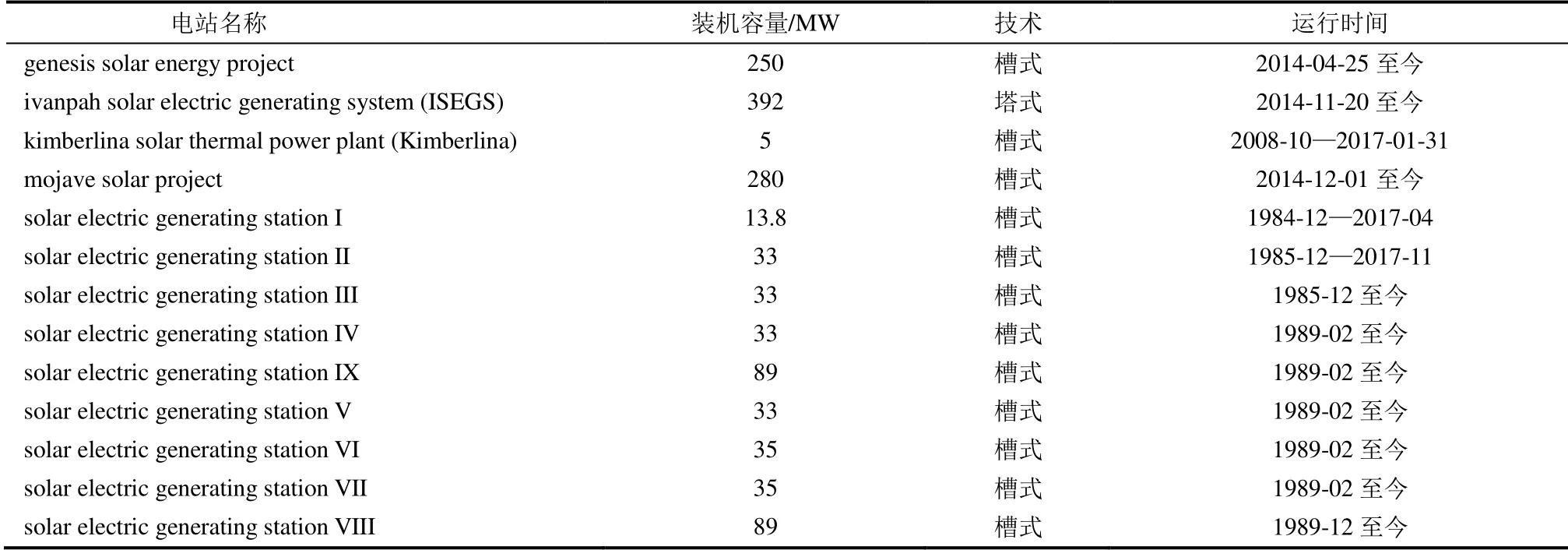
表1 电站数据信息Tab.1 Data information of the power plants

根据上述6 个位置，从NOAA[23]获取附近气象站在该时段的气象数据，包括8 大气象参数：温度（℃）、降水量（mm/h）、降雪量（mm/h）、积雪量（kg/m2）、空气密度（kg/m3）、地面太阳辐照度（W/m2）、大气顶部太阳辐照度（W/m2）以及云量（pu）。天气数据时间分辨率为1 h，与发电数据完全对应。

1.2 数据预处理

数据清洗过程中发现该电力数据集缺少2015年5月8日和2016年3月13日数据，观察上述2 天前后的发电数据，均无异常。由于当前可用数据量较大，因此忽略上述2 天的缺失数据。同时，删除上述6 个位置这2 天的所有天气数据。

针对聚类分析，本文将电力数据分割为24 h 的日发电样本，得到共计791 个样本，并将其转换为小时发电量的日百分比，以此观察发电模式的日内与日间变化。针对发电量预测，本文以给定回溯时间步长的历史气象参数和发电量作为特征构建模型输入，然后对各输入特征数据进行标准化，即转换为标准正态分布，以平衡特征间的数值差异，提高模型训练的速度与稳定性。

2 方法

2.1 近邻传播聚类算法

AP 聚类算法通过数据点间的信息传递，按照给定规则经过多次迭代来确定适合成为聚类中心的数据点，进而完成聚类[24]。与其他聚类方法相比，AP 聚类算法的运算效率较高且结果稳定，聚类质量高于K-means 聚类算法，且无需事先确定需要聚类的数量[25]。

AP 算法的核心为更新2 个矩阵：吸引度矩阵R，r(i,k)代表从i到k的消息，用来判定点k是否适合作为数据点i的聚类中心；归属度矩阵A，a(i,k)代表从k到i的消息，用来判定数据点i选择数据点k作为其聚类中心是否合适。最终，对点i，满足的点k即为其类中心。此外，算法还用到相似度矩阵S，s(i,k)代表点i和点k的相似度，一般采用2 点之间欧氏距离的相反数，而s(i,i)称为参考度，一般将其设为S的中位数。

算法具体实施步骤如下。

1）将吸引度矩阵R和归属度矩阵A都初始化为0，计算相似度矩阵S。

2）按照式(1)迭代吸引度矩阵：

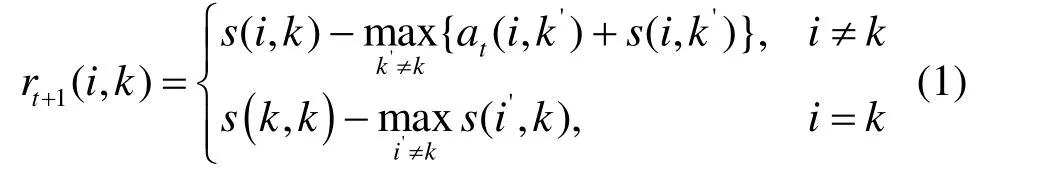
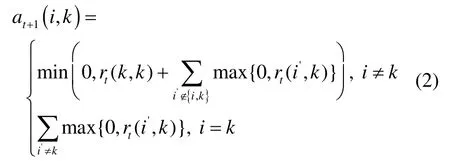
3）按照式(2)迭代归属度矩阵：

4）引入阻尼系数λ，以增强计算的数值稳定性：

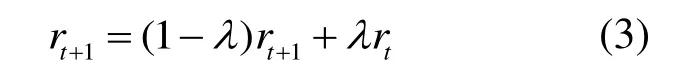
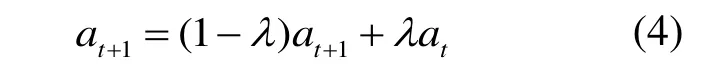
重复迭代上述步骤2）、3）、4），直到类中心稳定或者达到设定的迭代次数。

根据本文数据情况，选取算法的参考度为欧氏距离相似度S的中位数，阻尼系数为0.5，最大迭代步数为200，且当类中心保持15 次迭代不发生改变时认为算法收敛。

2.2 长短期记忆神经网络

RNN 包括输入层、隐藏层及输出层，隐藏层内的节点相互连接，其当前时间的输入包含来自输入层的输入以及上一时刻隐藏层的输出，因此RNN 能对历史信息进行有效记忆[26]。图2 为典型RNN 结构。

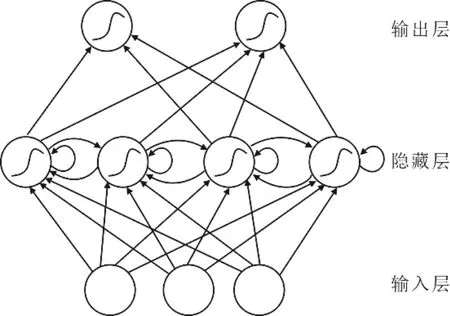
图2 RNN 结构Fig.2 The RNN structure

RNN 在遇到时间序列较长的数据时，由于隐藏层神经单元之间连接紧密，会出现梯度消失或爆炸的情况，因此不适于较长时间序列的数据处理[27]。对此，LSTM 神经网络在RNN 的基础上加入新的神经单元，解决了梯度爆炸的问题[28]。LSTM 神经网络包括记忆单元、输入门、输出门以及遗忘门，其神经网络结构如图3所示。

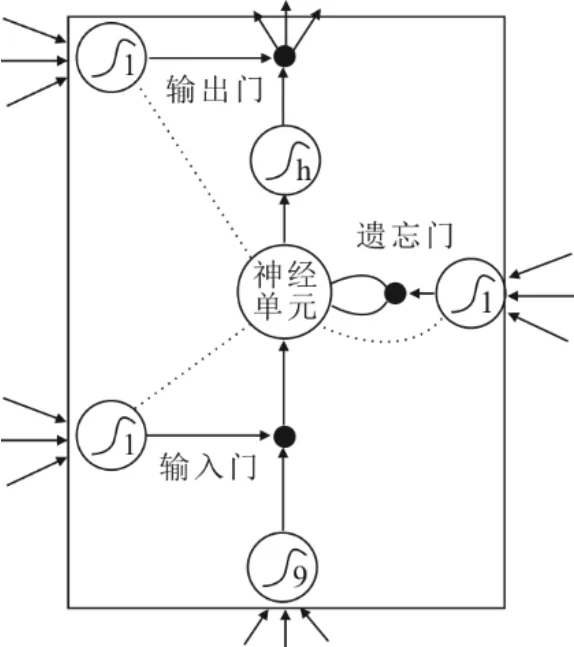
图3 LSTM 神经网络结构Fig.3 The LSTM neural network structure

LSTM 神经网络的前向与反向传播计算已经非常成熟，在此不再赘述。根据本文数据情况，选取输入特征的时间步长为1 h，并根据网格搜索优化神经网络超参数。

3 实验与结果

3.1 气象参数与光热发电相关性分析

气象参数对光热发电具有决定性的影响。在以往的太阳能电站发电量预测研究中，往往只针对少数参数如环境温度、太阳辐照度进行分析，对其余天气因素的影响分析较少[29-30]。这在很大程度上影响了光热电站发电量预测的准确度，尤其在连续阴雨、降雪以及极端天气的情况下。

为了研究1.1 小节6 个地理位置的气象参数对光热电站发电量的影响，本文计算各气象站气象参数与发电量、小时发电量日百分比之间的皮尔森相关系数，根据计算结果筛选有效特征。6 个气象站气象参数与发电量（散点）和小时发电量日百分比（柱状）的相关系数如图4 图所示。

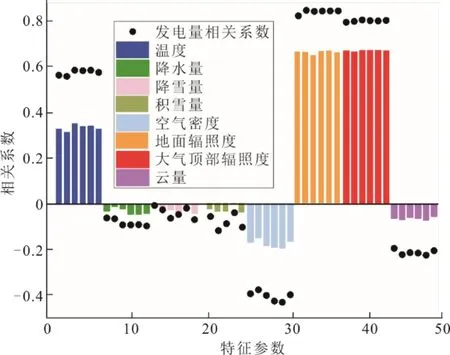
图4 6 个气象站气象参数与发电量（散点）和小时发电量日百分比（柱状）的相关系数Fig.4 Correlation coefficients between the meteorological parameters of 6 meteorological stations and the power generation(scatter diagram),the daily percentage of hourly power generation(columnar diagram)

由图4 可见，6 个气象站的气象参数与发电量间的相关性强于其和小时发电量日百分比之间的相关性，但各气象参数的相关性强弱排序基本一致：地面太阳辐照度>大气顶部太阳辐照度>温度>空气密度>云量>降水量≈积雪量≈降雪量。

3.2 聚类分析

为了更好地挖掘光热发电的行为特征及其受气象参数的影响差异，本文运用AP 聚类算法对小时发电量日百分比数据样本进行聚类，得到85 个类别。聚类结果的评价指标中轮廓系数（SC）、Calinski-Harabasz 指数（CH）和戴维森堡丁指数（DB）分别为146.06、0.76 和0.26，表明聚类质量高。进一步，根据类样本的数量将85 个类分为代表类A 类、少数类B 类以及异常类C 类。其中：代表类A 类满足类内样本数量大于总样本数的1%，即类内样本数量≥8；少数类B 类的类内样本数量在2～7 之间；异常类C 类的类内样本数量仅为1。图5 为A、B、C 类日期分布。

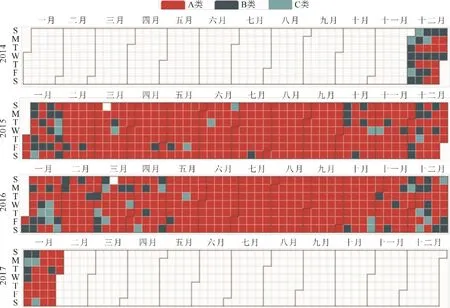
图5 A、B、C 类日期分布Fig.5 The type A,B and C date distribution map

通过对比气象参数与所有样本和A、B、C 类样本相关性变化（图6）。由图6 可见：A 类进一步强化了发电模式与强相关气象参数（地面太阳辐照度、大气顶部太阳辐照度、温度和空气密度）的相关性，结合其样本占比83.8%（24 类），可认为A类代表了主流发电模式；B 类则明显弱化了发电模式与气象参数的相关性，其样本占比11.6%（25 类），说明该部分数据更多地体现了气象条件以外的其他系统因素，如人为操作对发电情况的影响；而C类不仅数量最少，样本占比4.6%（36 类），也进一步减弱了气象条件对发电的影响，可能代表了发电系统所经历的各种意外状况。

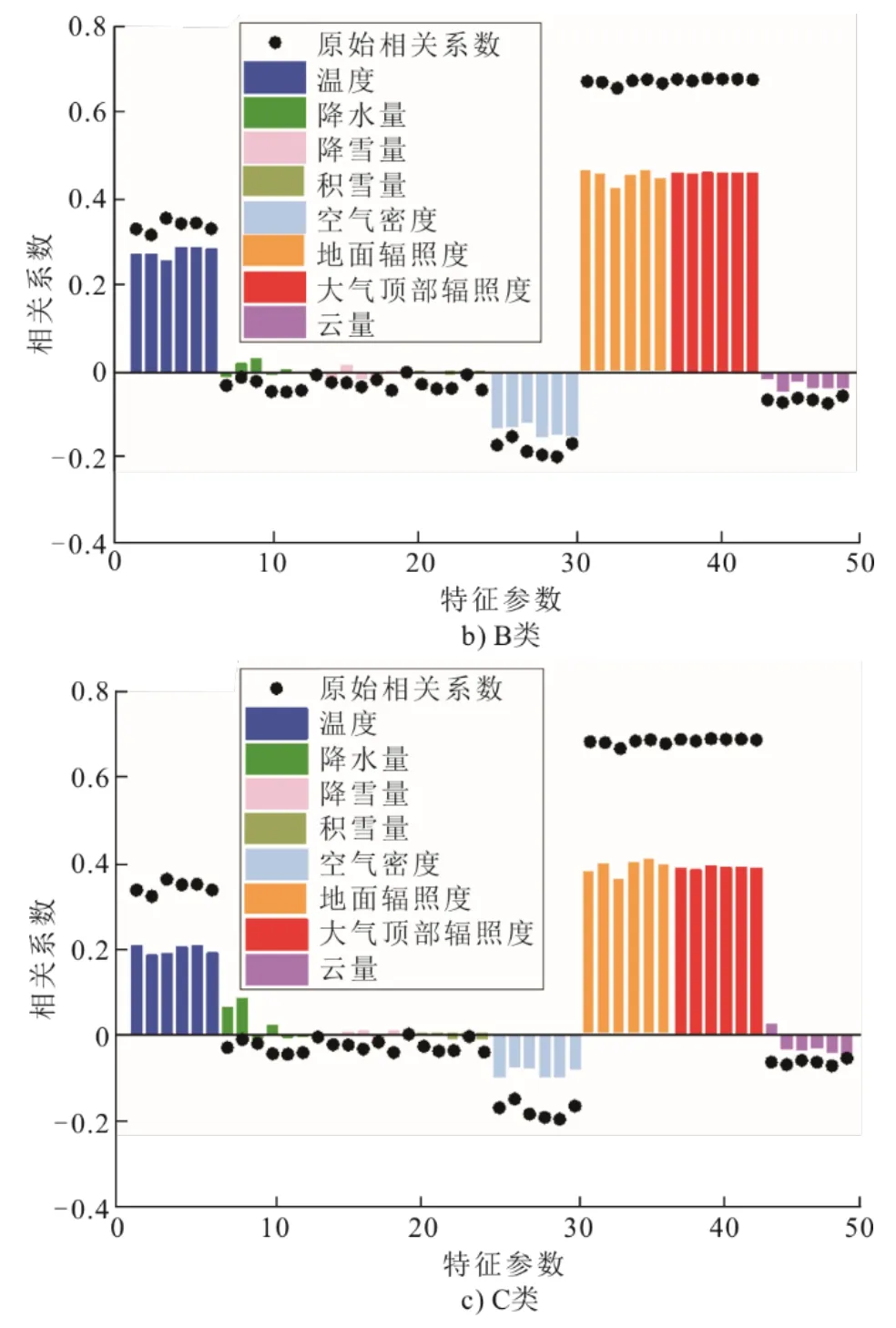
图6 气象参数与A、B 和C 类样本相关系数Fig.6 Correlation coefficient diagram of meteorological parameters and type A,B and C samples

根据聚类结果，本文选取A 类中日发电量为0的发电模式（A0）和典型晴天发电模式（A1）为例来说明不同类别发电模式下气象参数对发电的影响差异。图7 为影响0 发电量模式（A0）的主要气象参数箱线图，图中红色曲线为平均值。由图7 可以看出，在A0 中，云量、降水量、降雪量和积雪量4 个与总体样本相关性最低的气象参数值明显比其他发电模式下大。这与物理常识相符，但是在以往大样本数据的分析中并没有得到体现，这直接影响后续预测模型对气象参数特征的选择，进而影响预测精度。

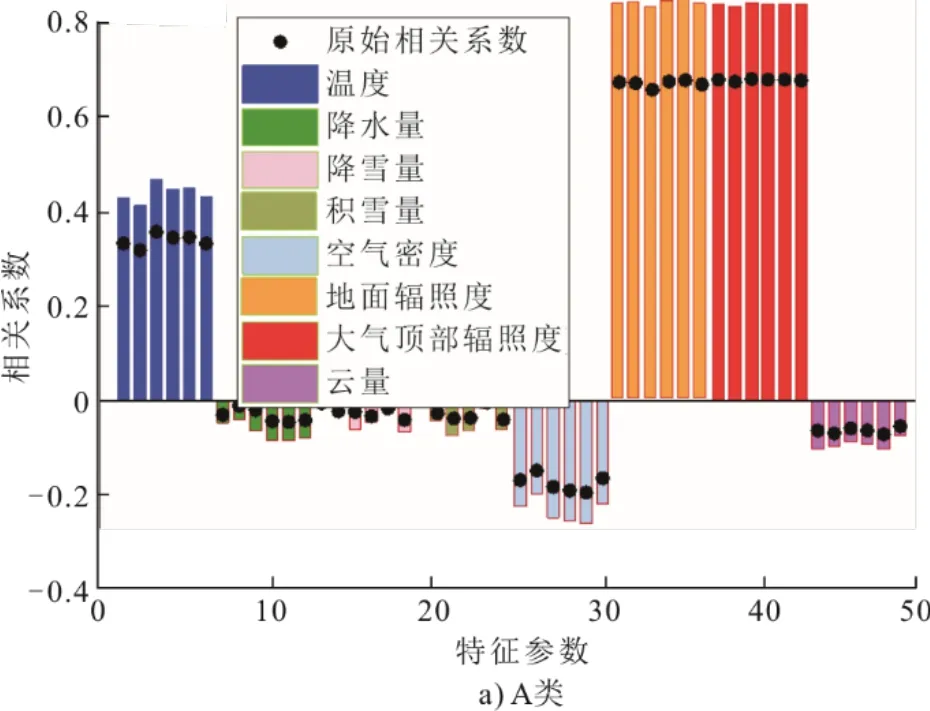
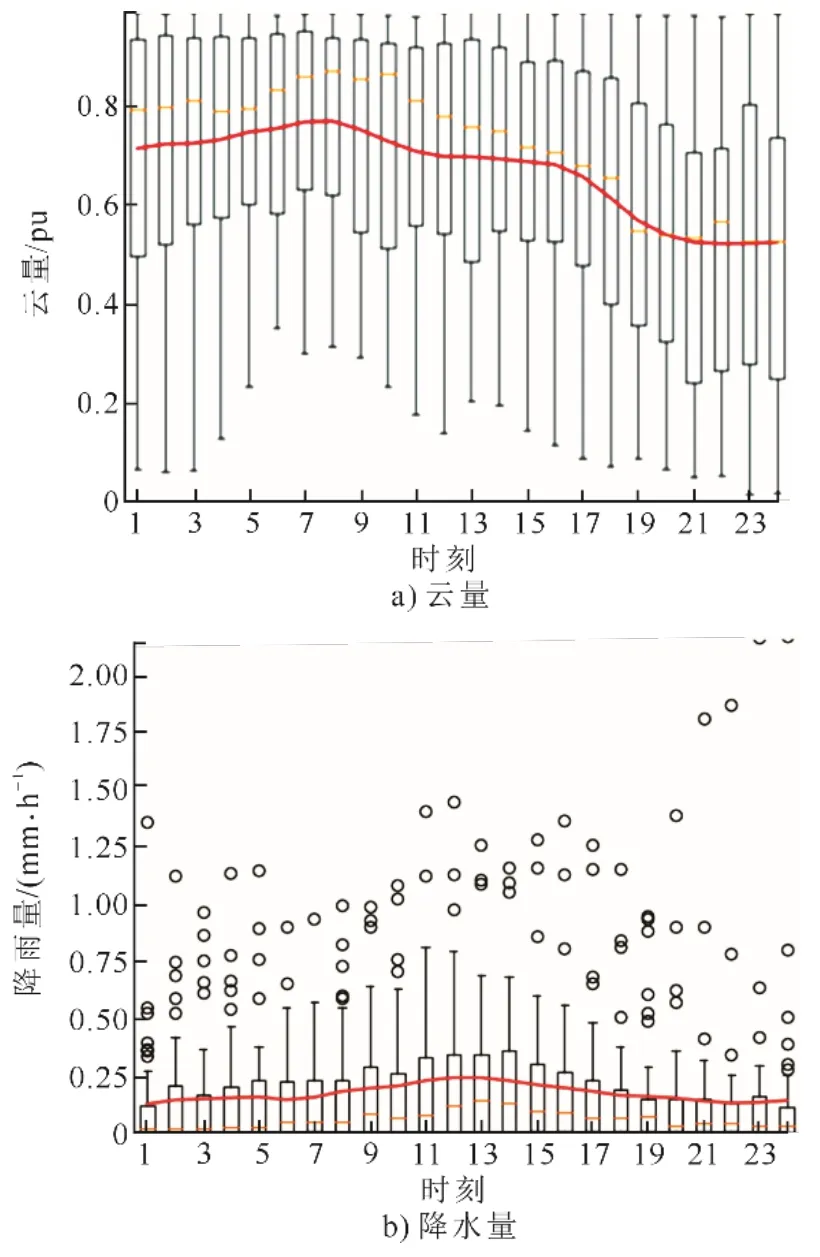
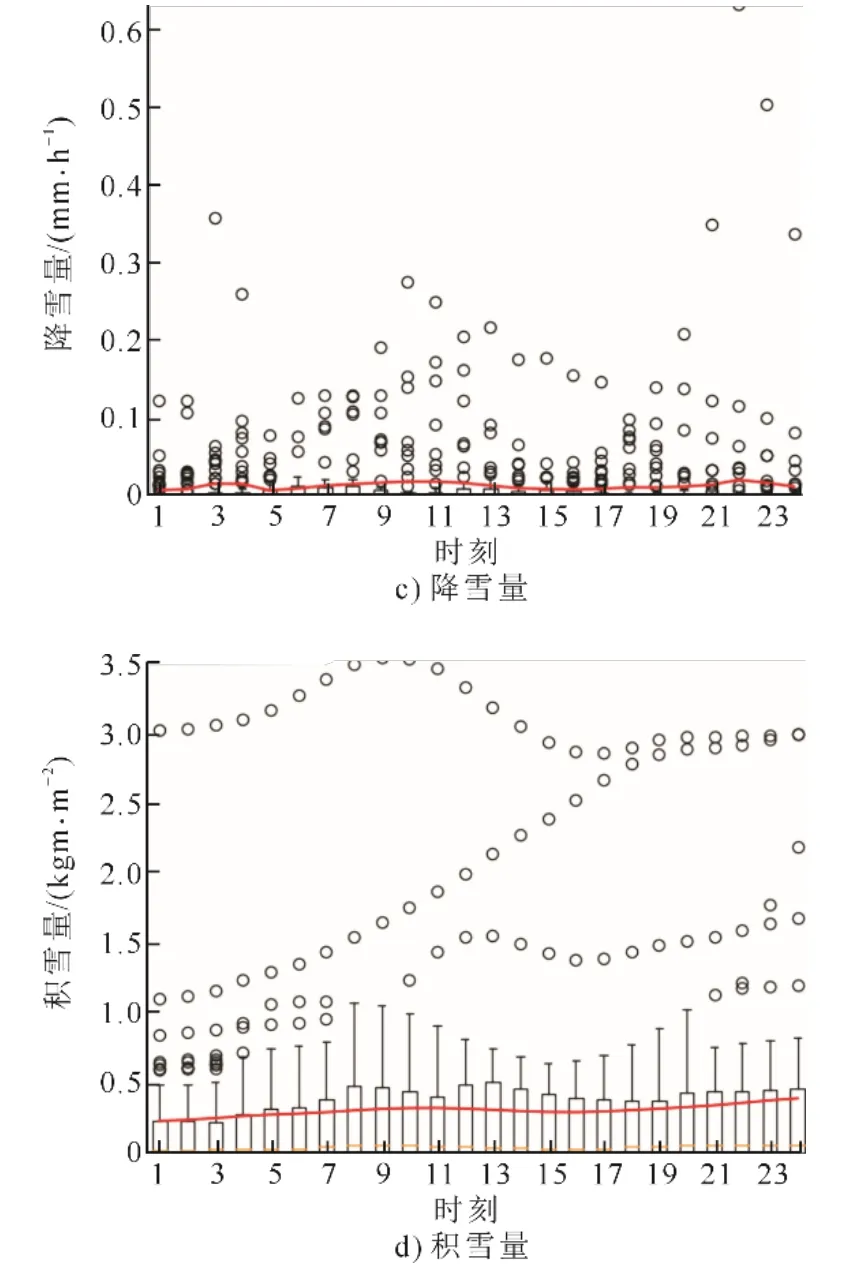
图7 影响0 发电量模式（A0）的主要气象参数箱线图Fig.7 Box plot of main meteorological parameters affecting 0 generation model(A0)

图8 和图9 分别为典型晴天发电模式（A1）的样本箱线图以及与气象参数的相关系数对比。由图8和图9 可见，典型晴天条件下，发电模式与地面太阳辐照度、大气顶部太阳辐照度、温度和空气密度这4 大气象参数间的相关性得到了进一步强化。因此，众多研究的预测模型在晴天条件下均表现较好[26]。2 种发电模式下气象参数对发电的影响差异反映了面对不同发电模式或者气象模式时，灵活选取气象参数特征，构建相应预测模型的重要性。

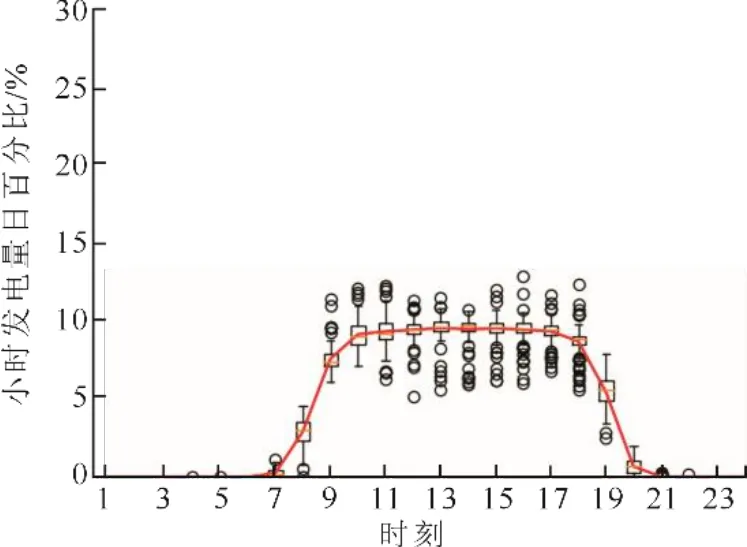
图8 典型晴天发电模式（A1）的样本箱线图Fig.8 Sample box plot of typical sunny day power generation model(A1)

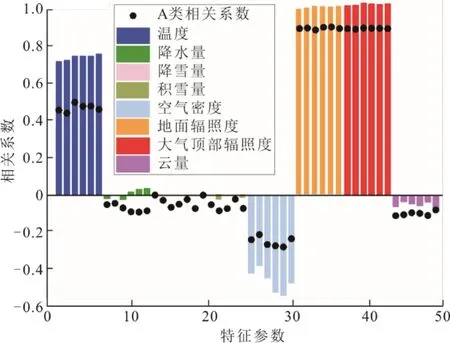
图9 典型晴天发电模式（A1）样本与气象参数的相关系数对比Fig.9 Correlation coefficients of the samples of typical sunny day power generation model(A1)and meteorological parameters

3.3 LSTM 神经网络预测模型

根据上文相关性分析与聚类分析的结果，本节构建LSTM 神经网络基准模型和LSTM 神经网络增量特征模型。在基准模型中，以地面太阳辐照度、大气顶部太阳辐照度、温度、空气密度和云量这5 大与发电量相关性较高的气象参数，外加历史发电量构建LSTM神经网络时序样本作为模型输入特征；而增量特征模型除基准模型的输入特征外，加入降水量、降雪量和积雪量这3 个弱相关性气象参数作为模型输入特征进行训练。

本文以2014年12月1日至2016年12月31日的发电数据与气象数据作为模型的训练集，其中训练集数据的后10%作为验证集，以2017年1月1日至1月31日的数据作为测试集。本文选择2017年1月的发电数据作为测试集的原因是该月同时含有聚类结果中的代表类A 类（23 天）、少数类B 类（5 天）和异常类C 类（3 天），其中0 发电量日期为9 天，具备发电模式的典型性和代表性，可充分检验预测模型效果。

输入特征的时间步长为1 h，即根据前1 h 的发电量和气象参数预测下1 h 的发电量。采用tanh作为模型的激活函数，Adam 为模型训练的优化器，均方差作为损失函数，训练样本的批量更新大小为1 898（训练集数据量的10%），最终输出为发电量的预测值。采用网格搜索优化模型超参数，确定基准模型隐藏层为2 层，单元数为200。

基准模型在上述参数设置下调参训练过程损失函数如图10所示，由图10 可以看出，训练损失和验证损失都下降并且最终稳定至接近重合，这说明在该参数设置下，运行1 000 次迭代的训练效果较好。故将所有训练数据（包括验证集）用于模型的训练，并在1 000 次迭代后停止，得到训练模型。

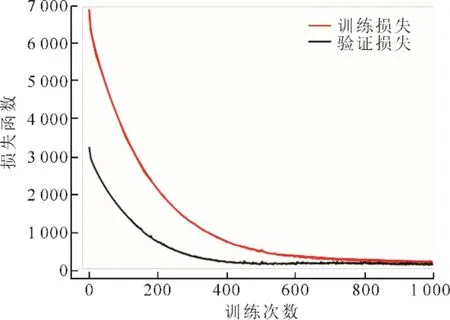
图10 调参训练过程损失函数Fig.10 Loss function diagram of parameter adjustment training process

对LSTM神经网络增量特征模型进行与基准模型相似的参数调试和训练。使用训练得到的LSTM神经网络基准模型和LSTM神经网络增量特征模型对2017年1月1日至1月31日每小时的发电量进行预测。发电量的预测值与实际值，以及不同类别下的日绝对误差如图11所示。

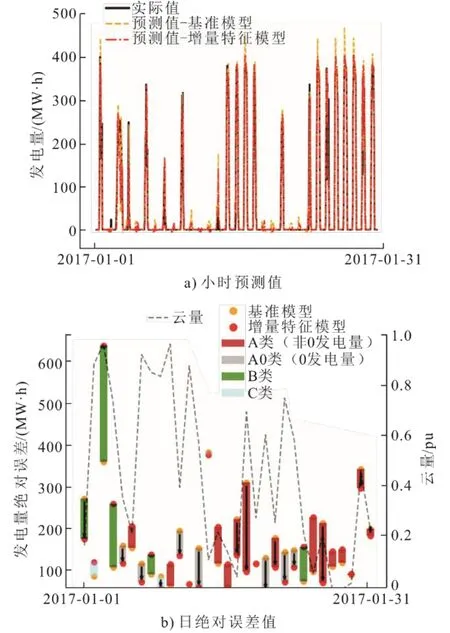
图11 测试集LSTM 神经网络基准模型和增量特征模型预测结果Fig.11 Prediction results of the LSTM benchmark model and the incremental feature model in test set

整个测试集内1月份31 天的实际总发电量为41 744.0 MWh，LSTM 神经网络基准模型与LSTM神经网络增量特征模型日发电量预测结果见表2。

由图11 和表2 可见，尽管总体预测精度只有微小改进，但在发电量为0 的日期中（A0），增加降雪量、降水量和积雪量作为模型输入特征的LSTM 神经网络增量特征模型，其日发电量总绝对误差由LSTM 神经网络基准模型的839.96 MW·h下降到373.32 MW·h，日发电量绝对误差占比由22.81%下降到10.41%，均下降2 倍以上。但是对于少数类B 类，增量特征模型的表现较基准模型反而总体降低。这反映模型在引入增量特征后，重新分配了对不同输入特征的拟合权重，使得模型对特定情况（如A0 类）的拟合能力有所提高，但由此也损失了对其他情况的泛化能力。由此可见，针对不同发电模式或者气象模式，应当灵活选取气象参数特征，构建相应预测模型，以提高预测精度。

表2 LSTM 神经网络基准模型与LSTM 神经网络增量特征模型日发电量预测结果Tab.2 Daily power generation prediction results of the LSTM benchmark model and the LSTM incremental feature model

4 结语

针对美国加州光热电站并网电力预测问题，本文提出了LSTM 神经网络预测模型构建方案，并实现91.41%的日发电量预测精度，可服务于实际电站。此外，根据聚类分析的结果，发现不同发电模式类别下，气象参数对发电的影响存在显著差异。而不同特征组合构建的预测模型，对不同气象条件下的光热电站发电预测能力同样存在差异。因此，根据聚类得到的发电模式类别，构建相应的特征组合预测模型，利用集成学习方法，有望进一步提高光热电站发电预测精度。