稳健最小二乘法在风电塔筒垂直度分析中的应用
2021-10-28李晓博汪俊波
程 帅,米 珂,李晓博,舒 进,陈 仓,兰 昊,汪俊波
(西安热工研究院有限公司,陕西 西安 710054)
随着风能开发利用技术的逐渐成熟,风电已成为目前最具规模的可再生能源之一,是我国能源转型的重要方向[1-2]。风电塔筒作为整个风电机组的支撑结构,具有重心高、承受水平力和倾覆弯矩较大等特点,其垂直度对机组安全及稳定性具有较强的敏感性[3],塔筒垂直度超标轻则导致风机塔筒驱动侧加速度超限,达不到设计运行标准,重则造成塔筒倾覆、倒塔等严重后果[4-5]。因此,提高风电塔筒垂直度分析精度并定期监测,对机组的安全稳定运行具有重要意义。
风电塔筒垂直度监测的主要方法有工程测量法、固定监测仪器在线监测法及三维激光扫描法等。郭倩倩[6]、曾群意[7]等利用工程测量法得到建筑物的特征点坐标,通过直接拟合法分析类似风电塔筒的高耸柱状结构垂直度,但该方法仅在人工剔除明显偏差测点的情况下,用原始测量数据直接拟合得到最终结果,其计算精度完全取决于测量点的误差大小。付晓敏[8]、李智峰[9]等分别发明了一种风电机组塔筒垂直度的在线监测装置,将静力水准仪与激光垂准仪分别应用在塔筒内部作为倾斜传感器监测风机塔筒的垂直度。丁克良[10]、王二民[11]等引入三维激光扫描技术测得建筑物表面的三维空间点云数据,经过简单去噪处理后,对高耸柱状结构进行垂直度分析,并与工程测量法结果进行了对比分析。
上述针对柱状结构垂直度监测分析中,核心都是获取表面特征点,拟合特征截面圆心后计算其偏移量,针对原始数据仅进行简单的去噪处理或人工剔除存在明显偏差的测点,计算精度对原始测量点的误差依赖较大。然而,由于现场测量条件复杂,加之塔筒结构受自然环境的侵蚀、安装工艺误差,以及人为损坏或其他异物撞击的影响所带来的表面损伤、结构不均匀等问题,使得原始测值序列存在粗差等异常测点,且数据偏离正态分布[12],诸多存在误差的测点在去噪处理或人工剔除时不易发现,最终导致计算结果失真。上述处理方法中均未考虑此情况,在拟合圆心时不具备消除此类误差的能力。故甄别粗差观测值并消除其影响,是提高分析精度的关键所在。
稳健估计作为一种具有较强抗干扰性、可识别观测值中偶然误差和粗差的数据处理方法,已广泛应用于诸多行业。陶叶青等[13]将稳健估计应用于测绘数据的处理中,解决了我国参心坐标系中控制点已知坐标含粗差、精度差等问题。陈开端[14]采用稳健总体最小二乘拟合,建立了地铁施工监测数据预测模型,该模型精度较高。李刚等[15]将稳健估计用于火电机组设备的状态评估模型中,解决了模型参数的偏差污染问题,参数具有较强稳健性。马洪磊等[16]在铁路平面线形拟合中以稳健估计为基础,采用选权迭代法识别并剔除非拟合线形内的粗差测点,显著提高了拟合参数的可靠性。此外,稳健估计理论与最小二乘法相结合在信息检索[17]、流程监控[18]、沉降预测[19]等多个领域得到广泛应用。
基于此,本文将稳健估计应用至风电塔筒的垂直度分析中,结合最小二乘圆拟合,通过Huber 选权迭代法,逐步消除测值序列存在的粗差、偶然误差等异常测点的影响,并结合实例对其分析过程和效果进行阐述,提高了拟合参数及垂直度分析的可靠性。
1 风电塔筒垂直度分析
1.1 垂直度监测特点与原理
垂直度指结构中心线在不同高度处相应底部点的偏移现象,又称为倾斜度[20]。风电机组塔筒是由多节塔段组成的高耸圆台状结构,在安装阶段法兰平面度细微偏差、接触面清理不到位、螺栓预紧力不均匀等,运行阶段基础不均匀沉降、长期风载或其他人为因素等情况都会造成其垂直度超标。
风电塔筒垂直度的工程测量法包括极坐标法和偏心测量法。其中,偏心测量法通过观测偏心点距离和角度得到圆心坐标,因其多余观测量少,测量结果易受偏心点选取、测距及仰角大小的影响,精度较低[5,10]。故本文以极坐标法测得塔筒特征截面原始坐标。
极坐标法是以测站点为中心,后视点定向,测定塔筒特征截面坐标点的方法(图1),其计算原理见式(1),坐标测量与计算过程此处不再赘述。
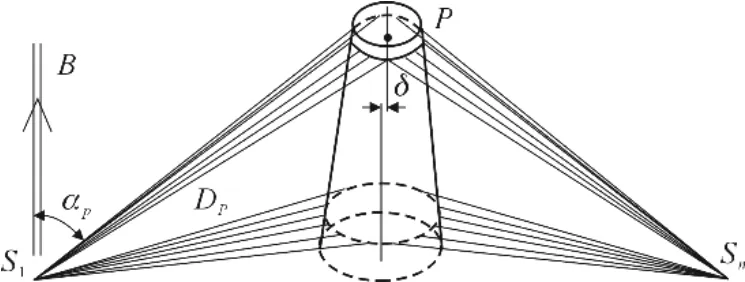
图1 极坐标法测量原理示意Fig.1 Schematic diagram of polar coordinate measurement principle
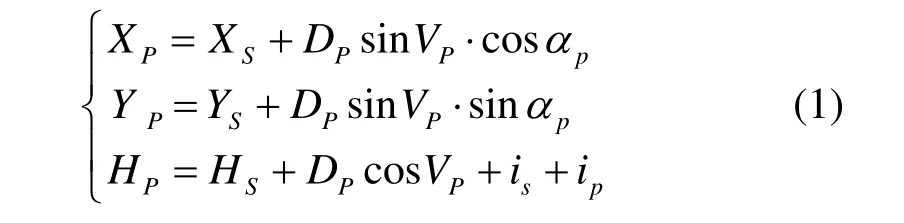
式中,XP、YP、HP分别为待测点坐标,XS、YS、HS分别为测站点坐标,DP为斜距,VP、αP分别为测站点Sn至待测点P的天顶距和方位角,is、ip分别为仪器高和棱镜高。
将原始测量数据处理,拟合得到各特征截面圆心坐标(XTi,YTi,HTi)及(XBi,YBi,HBi),按照式(2)进行风电塔筒垂直度计算(图2)。
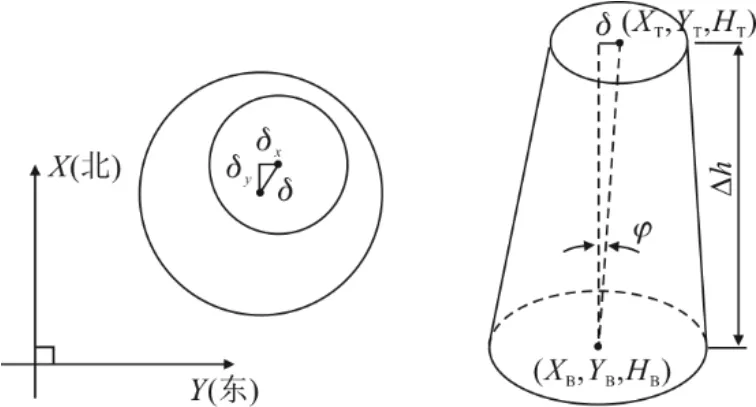
图2 垂直度计算示意Fig.2 Schematic diagram of perpendicularity calculation
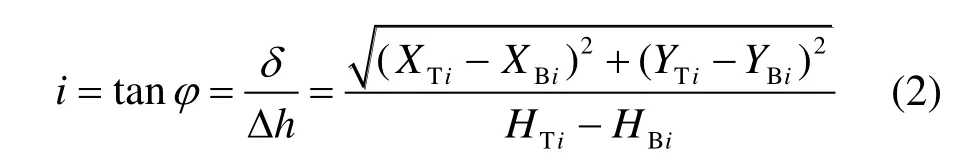
式中:i为风电塔筒垂直度(倾斜率),φ为倾斜角度,Δh、δ分别为两特征截面高度差及其圆心位移偏移量。
1.2 塔筒垂直度国家标准
针对风电机组塔架的垂直度限值,目前国内标准尚未统一,《风力发电机组塔架》(GB/T 19072—2010)及《风力发电机组装配和安装规范》(GB/T 19568—2017)规定在安装完成后其垂直度应不大于0.1%,而在《风力发电机组验收规范》(GB/T 20319—2017)规定机组验收时塔架总体倾斜度不大于8 mm/m。随着风电行业的发展和相关技术的进步,标准规范不断完善,最新《高耸结构设计标准》(GB 50135—2019)中新增了风力发电塔塔架倾斜率(垂直度)最大允许值为0.4%,根据笔者对甘肃及内蒙古地区风电场超过500 台风机塔筒垂直度的统计,认为其最大允许值定为0.4%较为合适。
1.3 误差来源
在风电塔筒垂直度监测中,原始特征点坐标测量存在的具有定量特性的系统误差如仪器照准误差、大气折光差、温湿度偏差等,可通过一定方法消除[20]。但由其他因素带来的偶然误差或粗差,无规律可循,其消除手段较为有限。如塔筒结构在长期风力、雨水等环境的侵蚀下,出现表面保护层剥落导致表面凹凸不平;制造及安装工艺问题导致法兰交界面存在细微的台阶状突变;塔筒受到人为损坏或其他异物撞击,在特征截面上留下凹陷印记等现象,诸如此类由自然因素或人因素所带来的塔筒表面损伤、结构不均匀的部位会直接导致特征点坐标失真,从而带来原始数据的粗差,最终导致特征截面拟合圆心的精度不稳定。传统最小二乘无法对原始坐标序列进行筛除,在拟合圆心时不具备消除此类误差以及其他异常误差的能力。
2 稳健估计最小二乘圆拟合
2.1 最小二乘圆拟合原理
最小二乘圆拟合是以观测数据为基础采用最小二乘法拟合得到圆曲线方程,最小二乘法以观测值残差的平方和最小作为最优估计准则,是迄今为止最主要、应用最广泛的参数估计方法[20-21]。设B为自变量x的系数矩阵,β为参数矩阵,L为观测值y的列向量,则误差估值V的方程为

最小二乘法原理为

风电塔筒外壁测量在同高处符合圆形分布,为得到其特征截面圆心,本文采用最小二乘圆拟合法对一系列观测数据进行预处理,根据圆参数方程构建多变量的二次目标函数
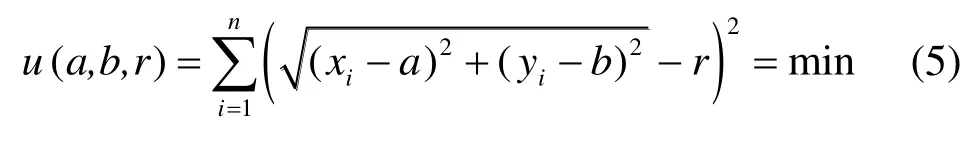
式中:(a,b)为圆心坐标;r为圆半径;(xi,yi)为所测特征截面圆弧采集点坐标;n为测点数量,测点数量即参与拟合的点数,为计算出参数a、b、r,测点数n应大于待估参数个数,即n≥3。
因目标函数u(a,b,r)中含有根号,计算极为复杂,令,则将此非线性的最小二乘问题转换为式(6)求解(d2–r2)最小值的线性问题。
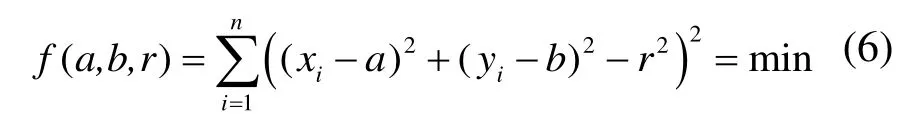
根据最小二乘法原理求相应参数,使得目标函数f(a,b,r)取得最小值,因平方和函数f(a,b,r)≥0,存在非负极小值,分别对目标函数式(6)的各参数求偏导,上述问题可转化为
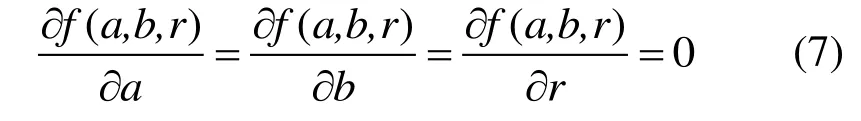
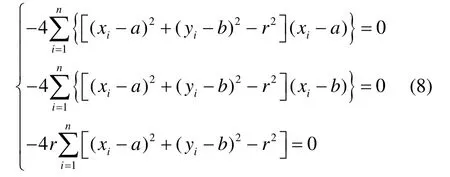
即可得到方程组
为求解式(8),引入新参数c,令c=r2–a2–b2,代入简化后,可将其优化成自变量为(a,b,c)的一阶线性方程组。
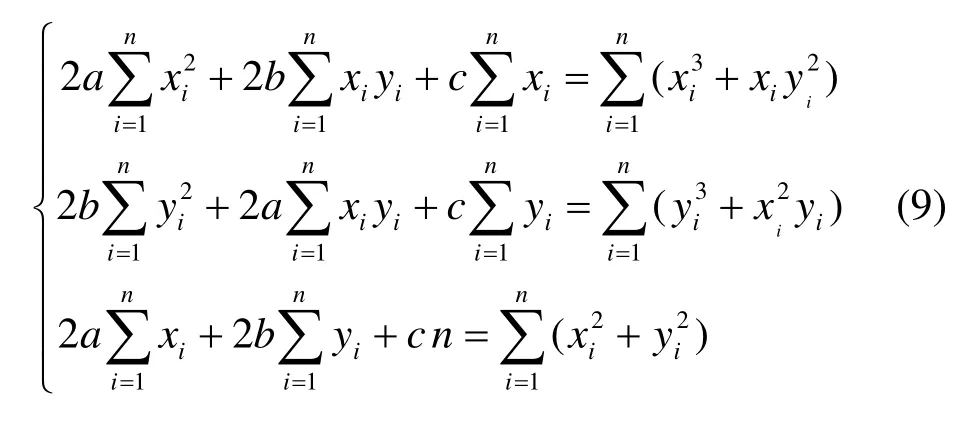
将各测量点(xi,yi)代入式(9)中,即可求得特征截面圆的拟合参数a、b、r。
2.2 稳健估计理论
最小二乘法是基于原始观测数据服从正态分布的前提,抵御粗差的能力有限。在实际观测中,粗差及偶然误差的出现无可避免,其概率最大约占观测总数的10%[21]。原始观测数据中存在此类误差会使拟合参数失真,极大降低垂直度监测精度。传统最小二乘法用统计及残差检测方法来剔除此类误差,具有很大局限性。针对最小二乘抗差性不足的缺陷,1953年GE.P.BOX 首先提出了Robustness概念,后经过Huber 等人[22-23]的研究发展,奠定了稳健估计理论的基础。稳健估计理论的原则是充分利用原始数据的有效信息,限制和排除有害信息,尽可能减弱实际观测中存在的粗差和偶然误差对参数估值的影响,进而得到最优参数估值。
稳健估计理论主要分为M 估计、L 估计和R 估计3 种类型,本文采用最具实用价值、应用最为广泛的M 估计法[23],即极大似然估计准则。为估计参数矩阵β,进行多次观测,得到观测值列向量L,f为随机向量L的密度函数,则有
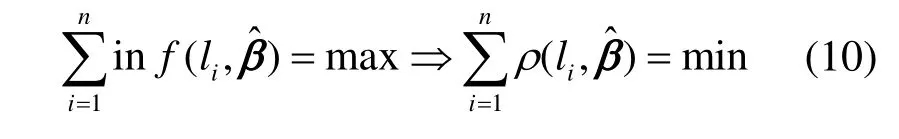
对式(10)求导,可得
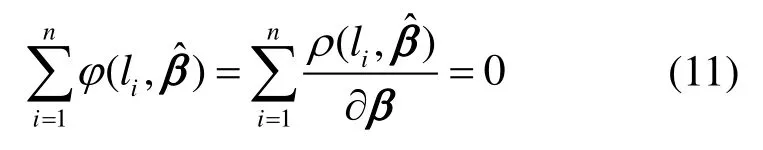
由式(10)—式(11)求出参数矩阵β的估值,即为M 估计。M 估计的方法有多种,本文选取易于编程实现、抗粗差能力强、应用最广泛的选权迭代法[24],其误差方程与式(3)一致,权函数矩阵为式(12),各权因子初始值为1,则
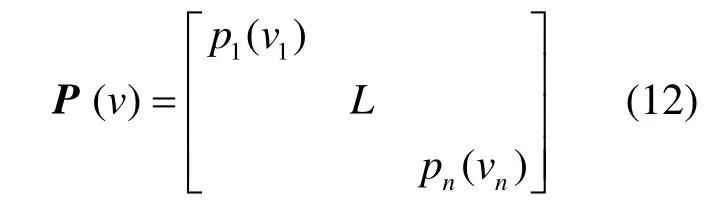
限制条件为
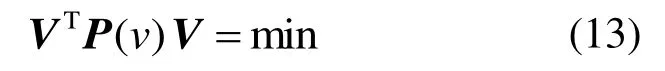
则法方程为

求解式(12)—式(14),得到待求参数和残差的第一次估值:
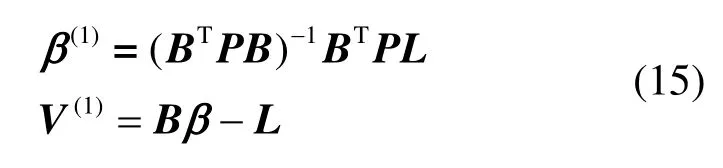
由初值V(1)确定各观测值新的权因子,实现粗差定位,构成新的等价权矩阵,再次解算算法方程式(14),如此迭代直至满足终止条件,得到最终的参数估值为:
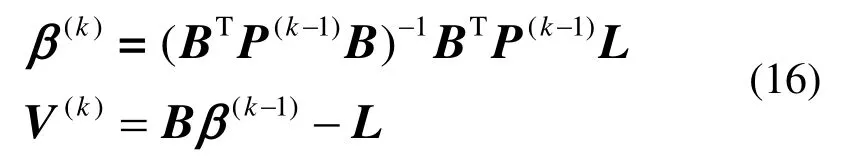
整个迭代过程中,含有粗差的测值的权值会逐渐减小,通过各测点残差值的大小可直观了解粗差等异常误差的大小及其测点位置。
2.3 Huber 迭代权函数
极大似然估计中的选权迭代法,其迭代权函数有多种选择,本文选用相应的Huber 迭代权函数,选取不同ρ函数,其φ函数及相应权函数也随之变化,且在迭代过程中,权函数也随改正数的更新而变化,根据Huber 法,ρ函数和φ函数[19,21]为:
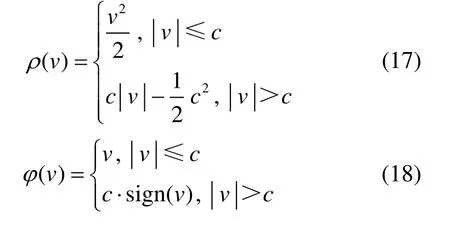
式中:v为误差函数,c为调和系数,按照“2σ准则”一般取2σ,对应的权函数为
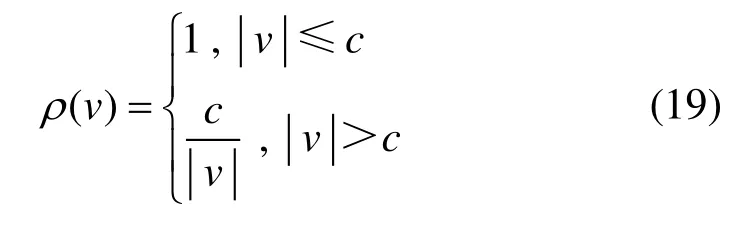
3 稳健最小二乘法计算塔筒垂直度
测得塔筒各特征截面测点原始坐标后,用所有测点参与拟合,采用最小二乘法计算各截面的圆心坐标和半径的拟合初值。由于各截面测点沿圆周均匀布置,高程坐标zi基本处于同一高程,为简化计算,在拟合过程中仅采用平面坐标(xi,yi)得到圆心平面坐标(a,b),高程坐标h由各拟合点的高程均值代替。取得圆心坐标及半径的初值后,计算各测点至拟合圆距离即拟合误差di,以此误差初值确定各观测值新的权因子,构成新的权因子矩阵,如此迭代直至满足迭代终止条件,即可实现逐步弱化和剔除粗差等异常误差测点的影响,得到各截面最终拟合圆心(a,b,h)及半径r的稳健结果。图3 为稳健最小二乘法计算风电塔筒垂直度算法流程,该算法采用Excel 内嵌VBA 语言编程实现。
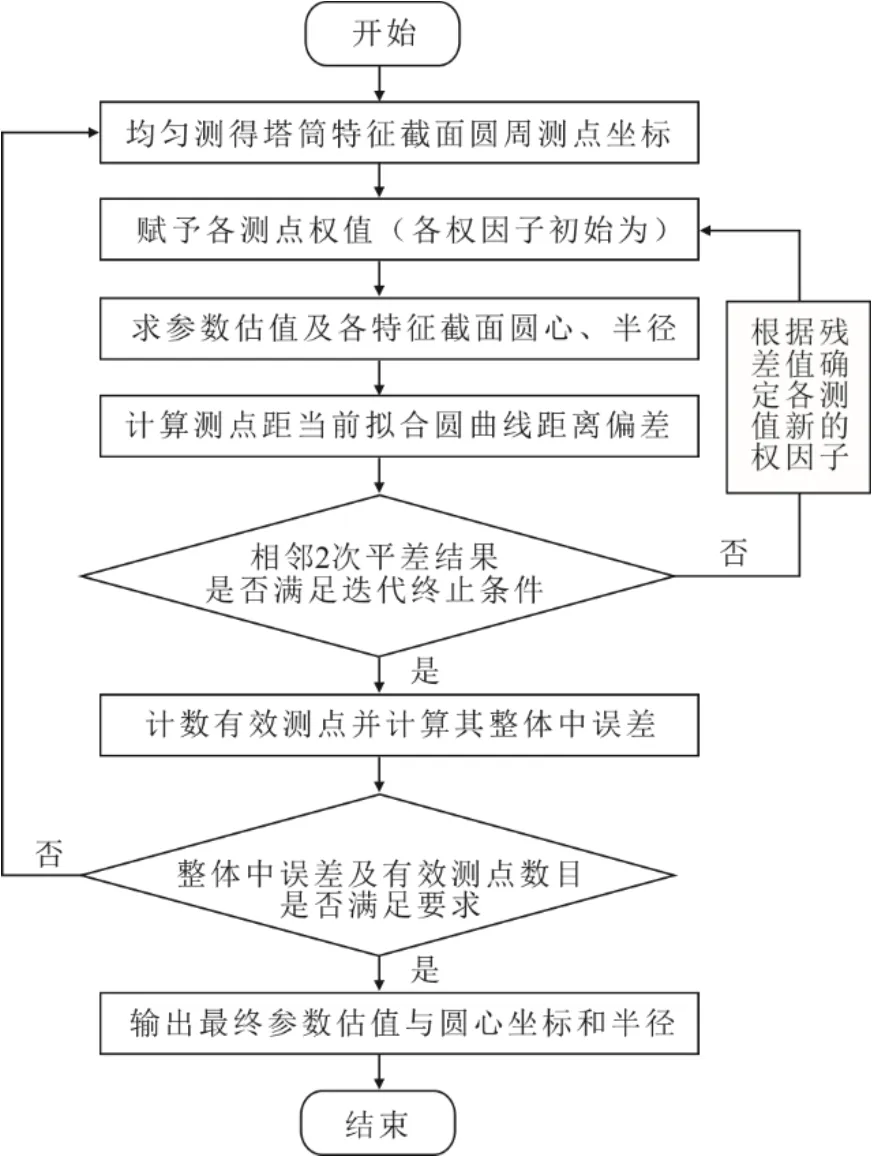
图3 稳健最小二乘法计算风电塔筒垂直度算法流程Fig.3 Flow of least-square in perpendicularity calculation of wind turbine tower
稳健估计选权迭代法的迭代终止条件一般以待估计参数平差值、观测值残差或单位权中误差作为判断基础。本文在垂直度分析算法流程中以相邻2 次待估参数平差值作为终止迭代条件,认为相邻2 次参数估计值差异小于10–4便可停止迭代。
若原始观测数值整体误差较大,虽经多次迭代后满足终止条件。但此时观测点权值接近0(小于1×10–3)的数目较多,有效测点数不足,最终估计值不可信。鉴于此,在分析算法流程中加入对整体测点中误差及有效点数的限制条件。当满足终止迭代条件后,考察整体测点中误差是否满足《工程测量规范》(GB 50026—2007)中关于高耸构筑物结构变形测量精度等级及相应测量点位中误差要求,且有效测点数目是否大于20 个,满足条件后方可计算最终风电塔筒垂直度。
4 应用实例
4.1 研究对象概况
以甘肃某风电场三期工程为研究对象,该工程安装风电机组单机容量为2.5 MW,采用圆柱形钢塔筒,由基础环和5 节塔筒组成,轮毂高度120 m,叶片长度70 m,风轮直径143 m,各节塔筒间的连接采用高强度螺栓连接。风电场地处典型的黄土高原地区,机组沿黄土梁顶布置,地质较为疏松,部分区域水土流失严重,垂直度监测尤为重要。
4.2 实例分析与验证
采用全站仪均匀测得塔筒底部、中部及顶部特征截面圆周各点坐标,各截面测点数量不少于40 个。采用上述稳健最小二乘法对原始数据进行处理,以其中某一台风机为例。为直观描述特征截面在稳健最小二乘法下的迭代过程与收敛情况,选择该风机的顶部截面,将各次迭代拟合得到的圆心坐标统一绘制在同一坐标系下(图4),图4 中序号为迭代次数,每次迭代得到的截面半径及其变化过程如图5所示。
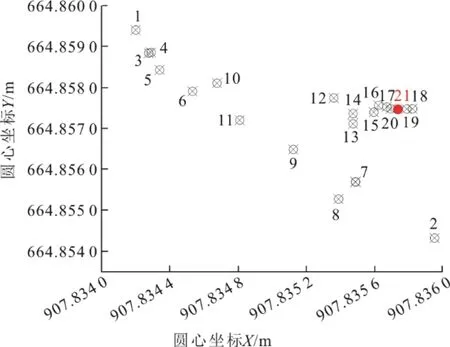
图4 截面圆心拟合过程Fig.4 The fitting process of section center
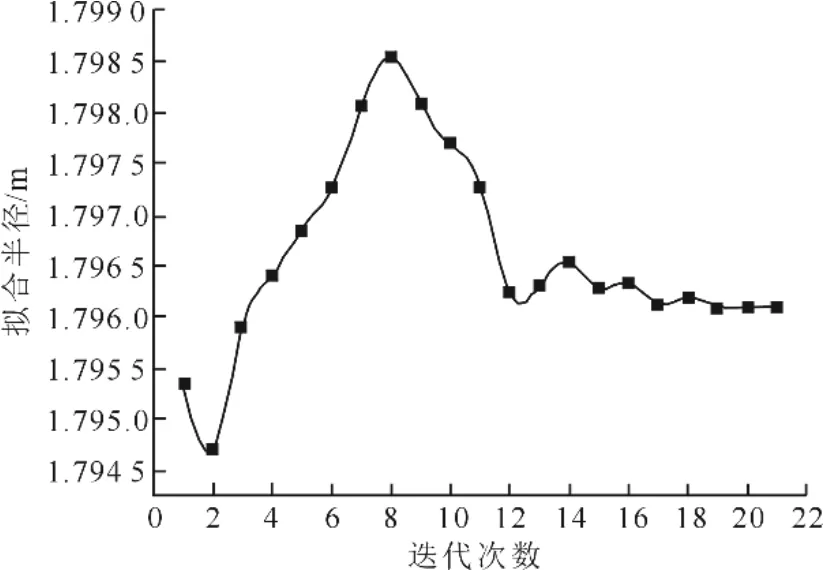
图5 拟合半径变化过程Fig.5 The change process of fitting radius
由图4 可知,空心圆点为迭代终止前圆心拟合结果,经过21 次迭代后满足迭代终止条件,最终圆心位置如实心圆点所示,坐标为(907.835 7,664.857 5),可见稳健估计过程中,圆心拟合结果在一定范围内不断变化,随着迭代次数增加,逐渐向最终圆心位置处靠拢。图5 中截面半径的拟合变化过程也同样反映此规律,迭代初期受异常测点影响,拟合半径在终值附近变动较大,随着迭代次数增加,半径的拟合结果逐渐趋于稳定。底部和中部截面与此类似。
为描述稳健估计最小二乘法在塔筒拟合过程中的精确性,绘制迭代过程中测点截面圆心拟合偏差均值与中误差的变化(图6),测点拟合最大偏差及平均偏差对比如图7所示。
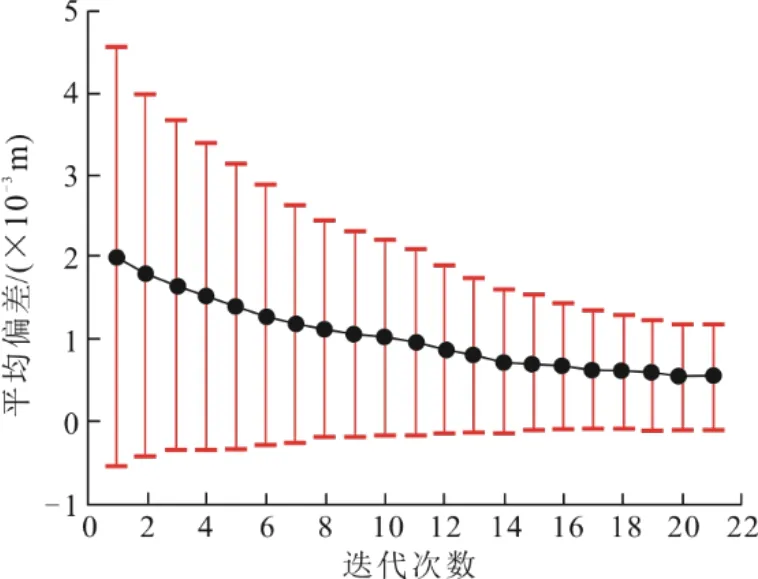
图6 拟合偏差均值与中误差变化Fig.6 Changes of the fitting deviation mean and its mean erro
由图6—图7 可知,在整个迭代过程中,测点拟合平均偏差及拟合中误差呈均匀下降趋势,平均偏差由2.1 mm 减小至0.5 mm,减小76%;中误差由2.6 mm 减小至0.6 mm,减小77%。测点拟合最大偏差由6.9 mm 降低至1.2 mm,降低83%,最大偏差在迭代初期降低速率较高,后续降低速率逐渐减小。总之,随着迭代次数的增加,测点拟合最大偏差、平均偏差及拟合中误差都逐渐减小,最后收敛稳定并达到迭代终止条件,得到误差更小、更为精确的圆心坐标及半径的最终拟合值,提高了截面圆心拟合精度。
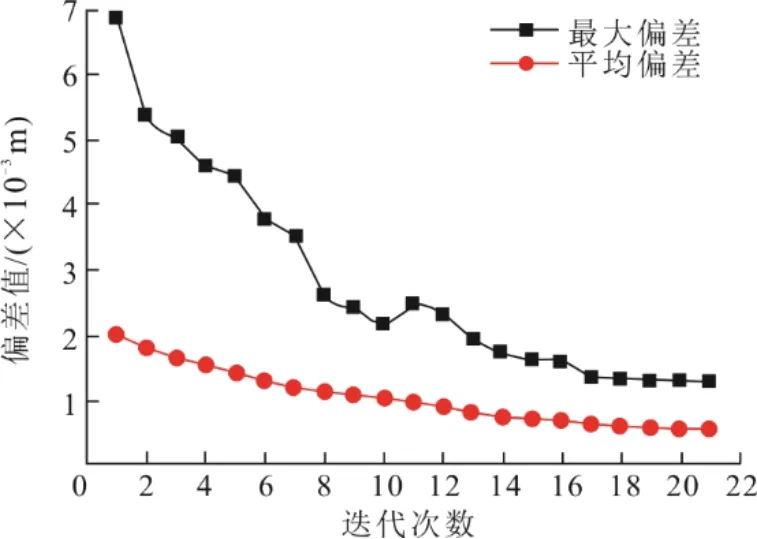
图7 最大偏差及平均偏差变化Fig.7 Variations of the maximum and average deviation
利用传统最小二乘法与稳健最小二乘法分别计算该风电塔筒垂直度,结果见表1。
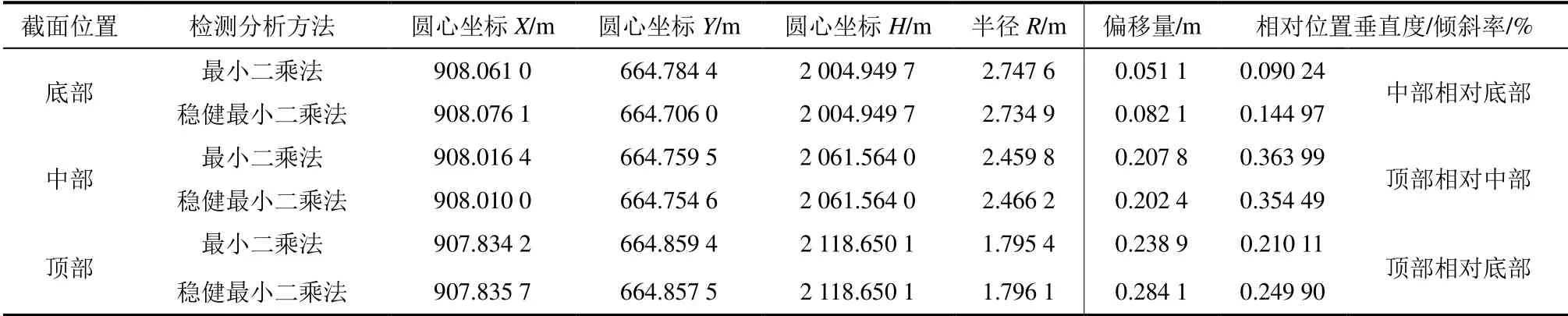
表1 塔筒垂直度计算结果对比Tab.1 Result contrast of the perpendicularity calculation for the tower
由表1 可知,采用稳健最小二乘法进行数据处理后塔筒拟合圆心坐标及半径都有不同程度的差异,由于底部存在粗差点较多,2 种方法坐标拟合结果相对较大。对比塔筒整体垂直度(顶部相对于底部)计算结果,稳健最小二乘法所得偏移量及垂直度与传统最小二乘法的相差约19%,可见,稳健最小二乘法对截面圆心的拟合精度有较大提高。
4.3 权函数简化与粗差点识别
根据迭代权函数式(19),经过多次迭代后,含有粗差或偶然误差的奇异测值的权值逐渐减小,直至趋近于0,则可将权函数简化为
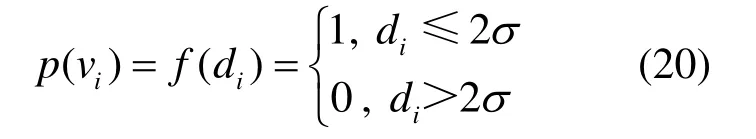
式中,di为各观测测点的残差值,即测点距拟合圆的距离。
以权函数式(20)进行迭代,在迭代过程中权值为0 的点即为粗差点或奇异测点,即可识别并剔除误差点,剔除时采用最大残差逐步剔除,即每次迭代后在di>2σ的所有测点中,剔除di最大的测点后继续迭代直至满足终止条件。
对比简化权函数计算结果,进一步说明稳健最小二乘在识别和剔除粗差测值的优越性。以上述风机顶部截面为例,统计有效测点(权值小于1×10–3的测点)数目为24 个,在此24 个有效测点中随机选取3 个点加入1~2 dm 的粗差。采用简化权函数及残差逐步剔除法,经过4 次迭代,逐步将粗差测点赋权值为0,各次迭代结果见表2。由表2 可知,权函数简化后可快捷有效识别并剔除粗差测点,对最终计算结果无影响,也进一步说明稳健最小二乘圆拟合法基本不受粗差、偶然误差等异常测值的影响。
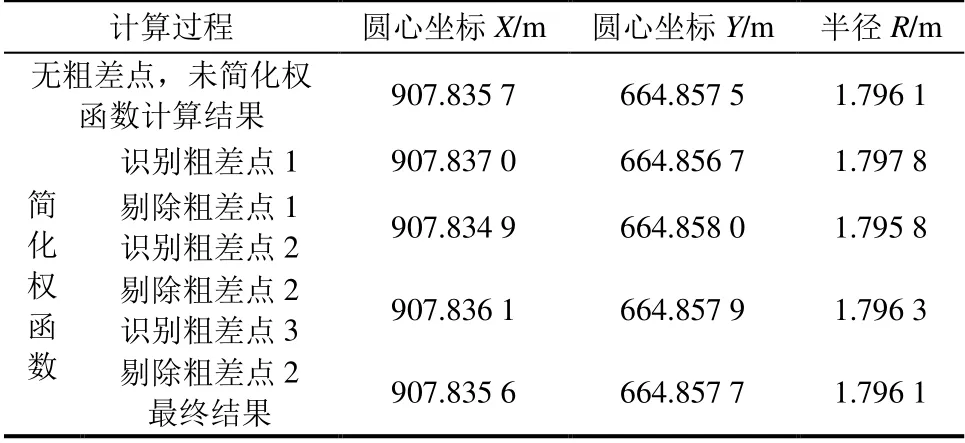
表2 简化权函数各次迭代结果Tab.2 The results of each iteration of the simplified weight function
5 结语
稳健最小二乘拟合法在截面圆心坐标和半径的拟合过程中能有效避免粗差、偶然误差等异常测点的影响,随着算法迭代次数的增加拟合结果逐渐趋于稳定,测点拟合最大偏差、平均偏差及拟合中误差都逐渐减小,有效提高了拟合参数及塔筒垂直度的计算精度。
简化权函数可快速识别并剔除原始测值序列中存在粗差、偶然误差等异常误差的测点,由自然或人为因素所带来的塔筒表面损伤、不均匀部位所导致的个别测点坐标失真的情况对最终计算结果无影响,基于稳健最小二乘法的垂直度分析具有较强的抗差能力。
本文方法易于编程实现,可推广应用于火电厂冷却塔、水塔、烟囱等其他类似高耸塔筒结构的垂直度分析中,对处理相关监测数据,提高监测精度具有一定参考价值。
