自然通风湿式冷却塔雨区阻力与变工况特性研究

余兴刚，宾谊沅，李 旭，陈 文，谢诞梅

（1.高效清洁火力发电技术湖南省重点实验室（国网湖南省电力有限公司电力科学研究院），湖南 长沙 410007；2.湖南省湘电试验研究院有限公司，湖南 长沙 410004；3.武汉大学动力与机械学院，湖北 武汉 430072）

自然通风逆流湿式冷却塔是火（核）电厂冷端系统中的重要热力设备，循环水在冷却塔内与空气接触发生对流传热传质，将从凝汽器中吸收的废热排入大气，达到维持凝汽器真空的目的[1-3]。冷却塔的热力性能直接影响机组凝汽器的真空，对机组的发电效率甚至运行安全性具有重要影响[4]。

冷却塔正常运行中，其出塔水温将随着机组负荷、循环水流量及环境气象条件等的变化而变化[5]。对于采用闭式循环水系统的机组，现有文献在开展循环水优化时大都忽略了冷却塔的影响而假定凝汽器入口循环水温度不变，将导致循环水优化的结果与实际存在一定偏差。郑姗[6]、王乾[7]等在开展机组冷端优化时虽然耦合了冷却塔的变工况计算，但文中均未给出塔内通风量的确定方法。曾德良等[8]基于进塔风速软测量方法构建了闭式循环水系统优化模型，提出了基于环境温度确定循环水泵的最优运行方式。鉴于循环水在线优化对计算结果的实时性要求较高，而冷却塔的二维和三维计算方法因计算过程复杂、计算量大导致实时性难以满足要求[9]。因此，有必要研究准确、快速的冷却塔热力计算方法。许多学者已在这方面开展过一定的研究。赵振国等[10]基于一维方法构建了冷却塔拟二维计算模型；张志刚等[11]提出了一种进塔风速的软测量方法，但该方法在计算进塔风速时假定条件较多；夏林等[12]基于由实测数据获得的塔内阻力系数构建了冷却塔的一维热力计算模型，但该模型中未考虑淋水密度对塔阻力系数的影响；李琦芬等[13]运用麦克尔焓差法和传统阻力系数计算公式对冷却塔的变工况特性进行了研究，然而传统阻力系数计算公式未考虑风速和淋水密度对阻力系数的影响。余建航等[14]提出了一种同时考虑喷淋区和填料区的湿式冷却塔一维热力性能预测模型。

本文以某自然通风湿式冷却塔为研究对象，通过对雨区气流阻力的计算得到了适用范围更广的该冷却塔雨区阻力系数计算公式，在此基础上运用麦克尔焓差法构建了冷却塔一维热力计算模型，并基于此模型研究了该冷却塔的变工况特性。

1 冷却塔热力计算模型

1.1 麦克尔焓差法基本原理

冷却塔内的热水主要通过接触和蒸发来散热，热水与空气之间既有热量传递又有质量传递，麦克尔在假设路易斯系数为1、冷却塔出口气态达到饱和及忽略冷却塔热质交换过程中水量的变化引起热量变化的前提下，推导出了麦克尔焓差方程[15]：

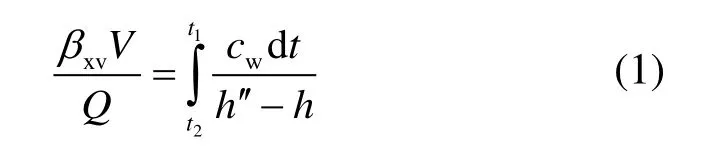
式中，βxv为淋水填料的容积散质系数，V为淋水填料体积，Q为冷却水流量，cw为冷却水的比热容，t1、t2分别为进出塔水温，h′′为与水温t相应的饱和空气比焓，h为湿空气比焓。

式(1)右侧可采用辛普森近似积分法求解，从而可简化为

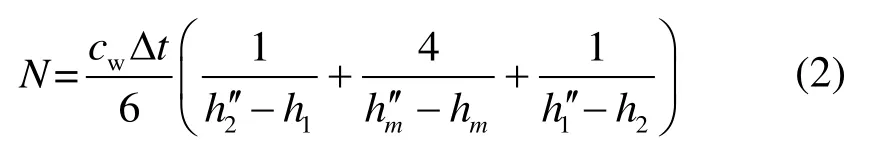
式中，N为冷却塔的冷却任务数，Δt为冷却水温差，h1和h2分别为进出塔湿空气比焓，h′′1、2h′和mh′分别为温度相当于进出塔水温和进出塔平均水温的饱和空气比焓，hm为进出塔湿空气比焓的平均值。

式(1)左侧为冷却塔的特性数，表征了在一定淋水填料和塔型下冷却塔所具有的冷却能力，一般由填料厂家提供，表示为

式中，Ω为冷却塔冷却特性数，A、n分别为常数，λ为气水比。

1.2 冷却塔抽力和阻力的计算

自然通风冷却塔内空气的流动依靠塔内外空气密度差形成的抽力驱动，空气在穿过塔内各部件时也会产生通风阻力，气流稳定时抽力和阻力应相平衡。冷却塔的抽力Z计算式为

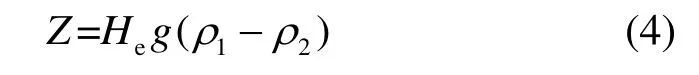
式中，He为塔的有效抽风高度，g为重力加速度，ρ1和ρ2为进出塔湿空气密度。

冷却塔的阻力H计算式为

式中，ζ为塔总阻力系数，ρm为进出塔湿空气平均密度，νm为填料层平均风速。

文献[16]给出的冷却塔总阻力系数计算方法为：

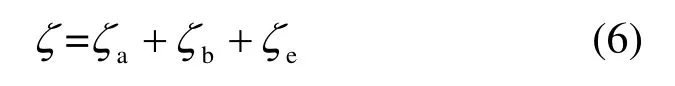
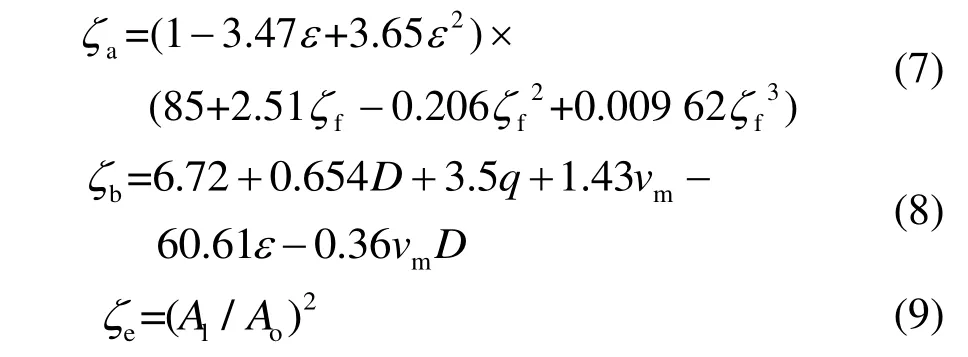
式中，ζa为不淋水时的气流阻力系数，ζb为淋水时雨区阻力系数，ζe为塔筒出口阻力系数，ε为塔进风口面积与进风口上缘塔面积之比，ζf为填料阻力系数，D为填料底部塔内径，q为淋水密度，Al为冷却塔淋水面积，Ao为塔筒出口面积。

1.3 雨区阻力系数计算方法

式(8)是文献[16]根据不同填料断面风速、淋水密度、塔内径和进风口高度组合的雨区阻力系数计算结果拟合得出。其适用范围为淋水密度 6～8 t/(m2·h)和填料断面风速1.0～1.2 m/s。现代大型冷却塔的淋水密度和填料断面风速实际运行范围通常超出了其适用范围，此时若仍采用式(8)计算雨区阻力系数将导致计算结果错误。因此，构建冷却塔热力计算模型时需要重新获取适用范围更广的雨区阻力系数计算公式。

对于一个直径为d的球形水滴，空气流过水滴时作用于水滴的力为：

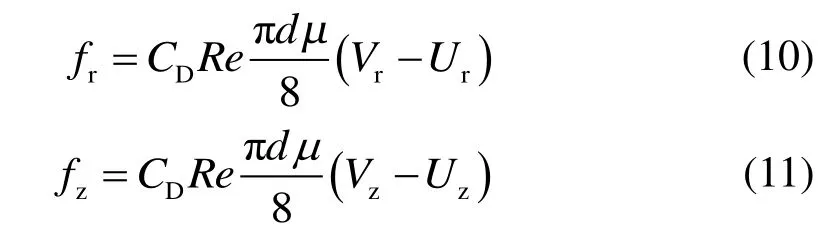
式中，fr和fz分别为气流作用于单个水滴的径向力和垂向力，CD为气流作用于水滴的阻力系数，Re为气流通过水滴时的雷诺数，ρ为气体密度，μ为气体动力黏度，Vr、Vz和Ur、Uz分别为气流和水滴的径向和垂向速度。

从式(10)和式(11)可以看出，求解气流作用于水滴的力需了解雨区气流和水滴的速度场。文献[16]对比了根据k-ε方法和简化气流流场计算得到的雨区阻力系数，结果表明二者相差仅3%。故本文将采用简化气流流场计算雨区阻力系数，并参考文献[16]对计算结果做3%的修正，进而得到最终雨区的阻力系数。简化流场中气流的垂向和径向速度计算公式为：

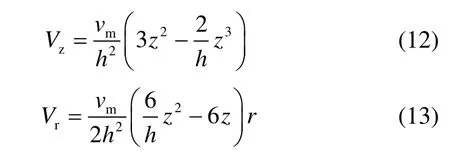
式中，h为冷却塔进风口高度，z 和r 为计算点的垂向和径向位置。

参考文献[16]，计算雨区气流阻力系数时忽略通风引起的淋水倾斜，即认为Ur为0，水滴的垂向速度Uz采用式(14)计算。

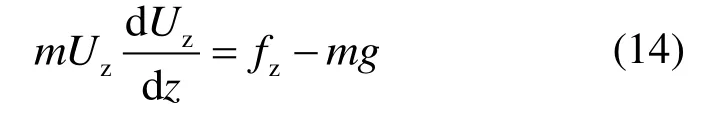
式中m为水滴的质量。

采用四阶龙格-库塔方法求解式(14)即可获得雨区水滴垂向速度的分布。

有了雨区气流和水滴的速度场即可根据式(10)和式(11)计算得到气流作用于水滴的力（即水滴作用于气流的阻力）。由于力为矢量不能直接相加，需先求出各点功率后再相加，雨区气流的径向和垂向阻力的功率计算公式为

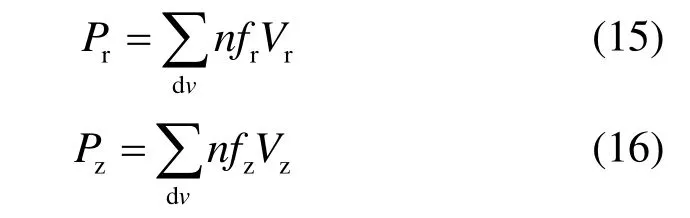
式中，dv为每一微元体的体积，n为每一微元体dv内水滴的数量。

由于冷却塔的阻力系数以填料层风速为基准，所以在计算阻力系数时需先将阻力功率除以填料层风速。雨区气流径向、垂向阻力系数计算公式为：

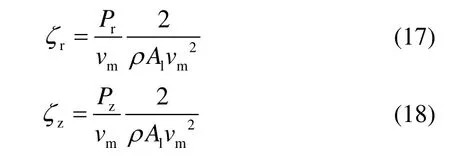
雨区气流的总阻力系数等于径向和垂向阻力系数之和。

2 冷却塔热力计算方法

冷却塔热力计算的目的主要是求解出塔水温，计算已知条件一般为环境气象状况（干球温度、相对湿度和大气压力）、循环水流量、冷却塔热负荷（或进塔水温）以及填料的热力和阻力特性。热力计算遵循的原则为冷却塔的冷却任务数和特性数相等、冷却塔的抽力和阻力相平衡，当计算出塔湿空气状态参数时假定出塔湿空气为饱和状态[15]。由于式(2)为非线性方程，与冷却塔冷却特性数相等对应的解可能有多个，但其真实解需同时满足3 个焓差均大于0，因此，在迭代计算过程中为获取真实解应加上这3 个限定条件。冷却塔热力计算流程如图1所示。

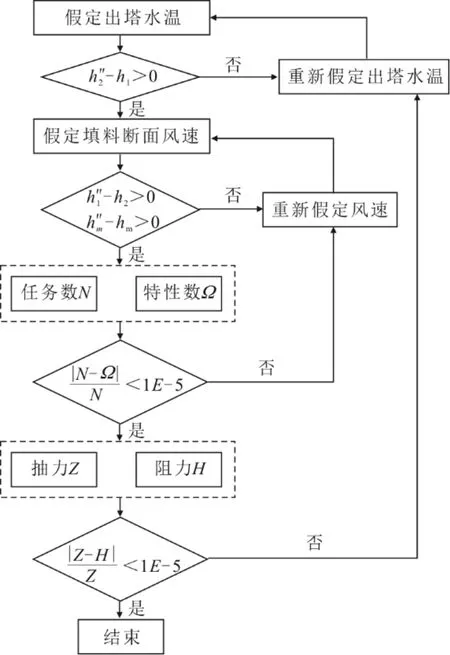
图1 冷却塔热力计算流程Fig.1 Flow chart of thermal calculation for the CT

3 计算模型准确性验证

本文选取某660 MW 火电机组配备的自然通风逆流湿式冷却塔为研究对象。冷却塔的淋水面积为10 000 m2，塔筒进风口标高为10.8 m，塔高为160 m。该机组冷却塔于2020年5月进行了改造，对填料、喷溅装置等进行了更换。

采用1.3 节方法计算了当淋水密度为3～8 t/(m2·h)和填料层风速为0.7～2.2 m/s 时该冷却塔雨区的阻力系数，选取的淋水密度和风速范围可覆盖冷却塔所有运行工况，计算结果如图2所示。

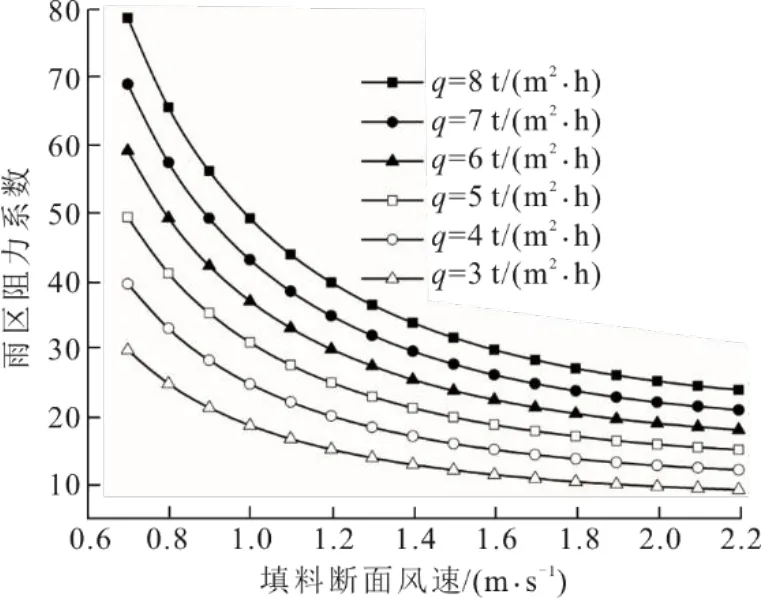
图2 雨区阻力系数计算结果Fig.2 Calculation results for rain zone resistance coefficient

文献[17]的实验结果表明当水滴的降落高度为8～10 m 时，水滴当量直径为2.8～3.0 mm。鉴于本文所研究冷却塔进风口高度为10.8 m，因此在计算雨区阻力时，水滴当量直径取为3.0 mm。

从图2 可以看出，雨区阻力系数随着淋水密度的增大而增大、随着填料层风速的增大而逐渐减小。不同淋水密度下雨区阻力系数随填料层风速的变化规律基本相同。

根据图2所示结果可拟合得到该冷却塔雨区阻力系数的计算公式，如式(19)所示。式(19)拟合结果的最大相对误差仅1%。

对于该冷却塔，当淋水密度分别为4、7 t/(m2·h)时不同填料层风速下式(8)和式(19)计算得到的雨区阻力系数如图3所示。从图3 可以看出：当淋水密度为7 t/(m2·h)、风速介于1.0～1.2 m/s 时，式(8)和式(19)的计算结果基本相同；而当水密度为4 t/(m2·h)或风速不在1.0～1.2 m/s 时，两式的计算结果则存在较大偏差。

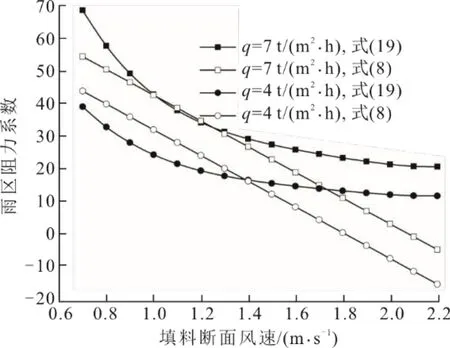
图3 雨区阻力系数计算结果对比Fig.3 The rain zone resistance coefficients calculated by different formulas

所研究的冷却塔在改造完成后进行了性能验收试验。采用所建立的冷却塔热力计算模型对试验工况进行了计算，计算结果和实测结果对比见表1。

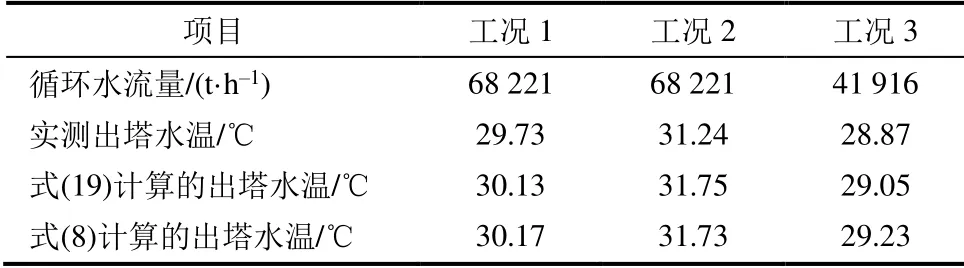
表1 计算结果与实测结果对比Tab.1 The calculated and measured values

由表1 可以看出，当采用式(19)计算雨区阻力系数时模型计算得到的出塔水温与试验实测数值相比偏高0.18～0.51 ℃，最大相对偏差为1.6%。可见，所建立的冷却塔热力计算模型可以准确地预测冷却塔的出塔水温，对于开展机组在线循环水优化和冷却塔性能诊断具有实际意义。

对于表1 中3 个试验工况，采用式(19)和式(8)计算得到的填料层风速见表2。

表2 塔内风速计算结果Tab.2 The calculated results of airflow velocity

当机组循环水泵运行方式为一机两泵时，冷却塔淋水密度为6.82 t/(m2·h)，处于式(8)的适用范围内，工况1 风速的计算结果也处于式(8)的适用范围内，工况2 风速的计算结果虽然超出了式(8)的适用范围，但从图3 可以看出此时风速偏离造成的阻力系数计算结果偏差较小，因而式(19)和式(8)计算得到的出塔水温偏差最大仅为0.04 ℃。而当循环水泵运行方式为一机一泵时，冷却塔淋水密度为4.19 t/(m2·h)，超出了式(8)的适用范围，从图3 可以看出此时式(19)和式(8)计算得到的雨区阻力系数存在较大偏差，进而导致两式计算得到的填料层风速和出塔水温的偏差增大。

4 冷却塔变工况特性分析

冷却塔正常运行过程中，其运行边界条件处于不断变化的状态，鉴于现有文献在研究冷却塔变工况特性时所采用的阻力系数计算模型存在一定局限性，有必要运用所得适用范围更广的阻力系数计算模型重新研究循环水流量、冷却塔热负荷、环境气象参数对冷却塔出塔水温的影响。

4.1 循环水流量

不同冷却塔热负荷、大气干球温度和相对湿度下循环水流量对出塔水温影响的计算结果如图4所示。图4 所考虑的循环水流量最大值和最小值分别对应表1 中一机两泵和一机一泵运行时的循环水流量。图4 中纵坐标为不同循环水流量工况下（其他条件均相同）的出塔水温与一机一泵工况下出塔水温的差值，100%热负荷对应表1 工况1 时冷却塔的热负荷。从图4 可以看出，冷却塔出塔水温将随着循环水流量的增加而升高，这主要是因为循环水流量增大后，塔内气流阻力将增大，使冷却塔的气水比降低，进而导致塔的冷却性能下降。循环水流量对出塔水温的影响将随冷却塔热负荷、大气干球温度、相对湿度的变化而变化。冷却塔热负荷越高，循环水流量的变化对出塔水温的影响越大，100%热负荷时一机两泵与一机一泵工况的温差比50%热负荷时的温差大0.55 ℃（图4a)）。大气干球温度越低，循环水流量的变化对出塔水温的影响越大，大气干球温度为10 ℃时一机两泵与一机一泵工况的温差比干球温度为30 ℃时的温差高0.58 ℃（图4b)）。循环水流量对出塔水温的影响还将随着大气相对湿度的降低而增大，大气相对湿度为0.60 时一机两泵与一机一泵工况的温差比相对湿度为0.90 时的温差大0.35 ℃（图4c)）。

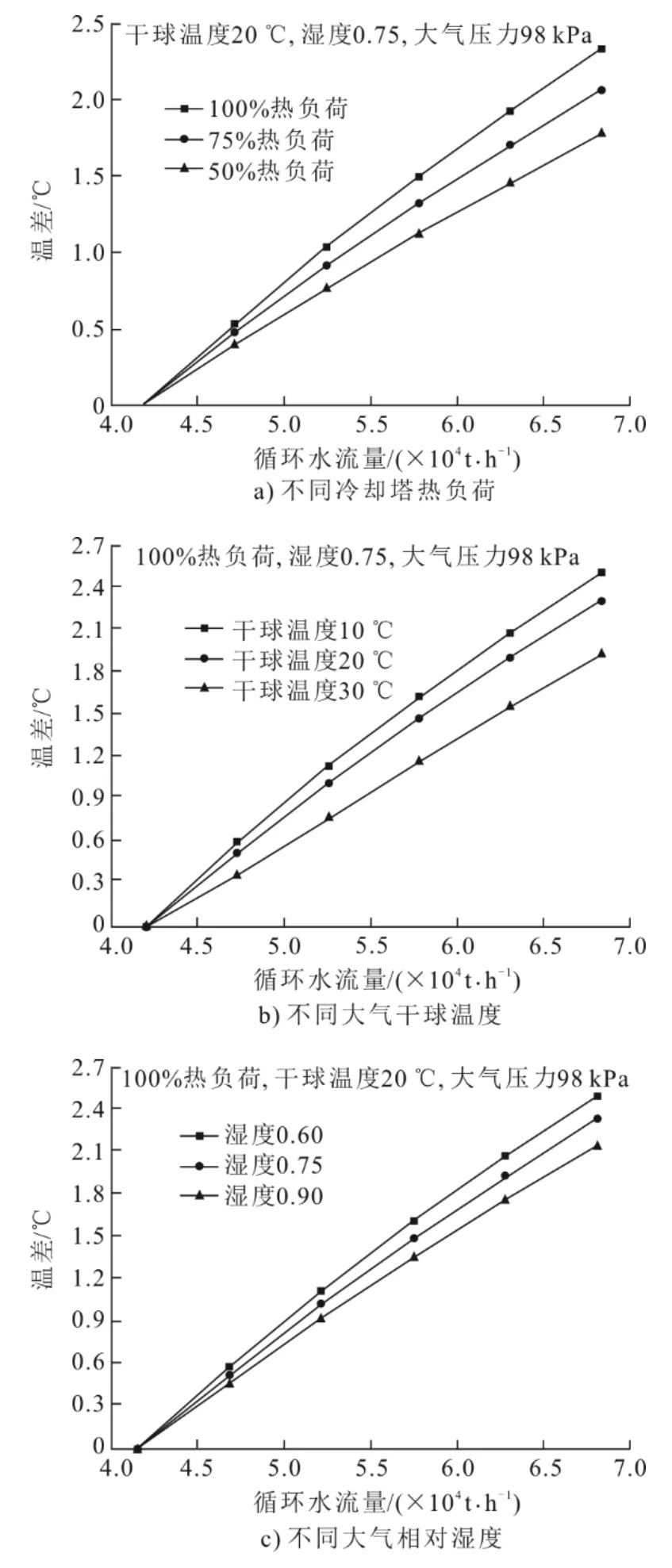
图4 循环水流量对出塔水温的影响Fig.4 Effect of circulating water flow on CT outlet water temperature

文献[18]在开展机组循环水泵运行方式优化时假定一机一泵、一机两泵和一机三泵工况下冷却塔出塔水温差为恒定值。从以上分析可以看出，这一假定将导致优化结果与实际存在一定偏差。

4.2 冷却塔热负荷

冷却塔的热负荷主要影响进出塔水温差。不同大气干球温度、相对湿度、循环水流量下冷却塔热负荷的变化对出塔水温的影响如图5所示。图5 中纵坐标为不同热负荷下的出塔水温与50%热负荷下出塔水温的差值。

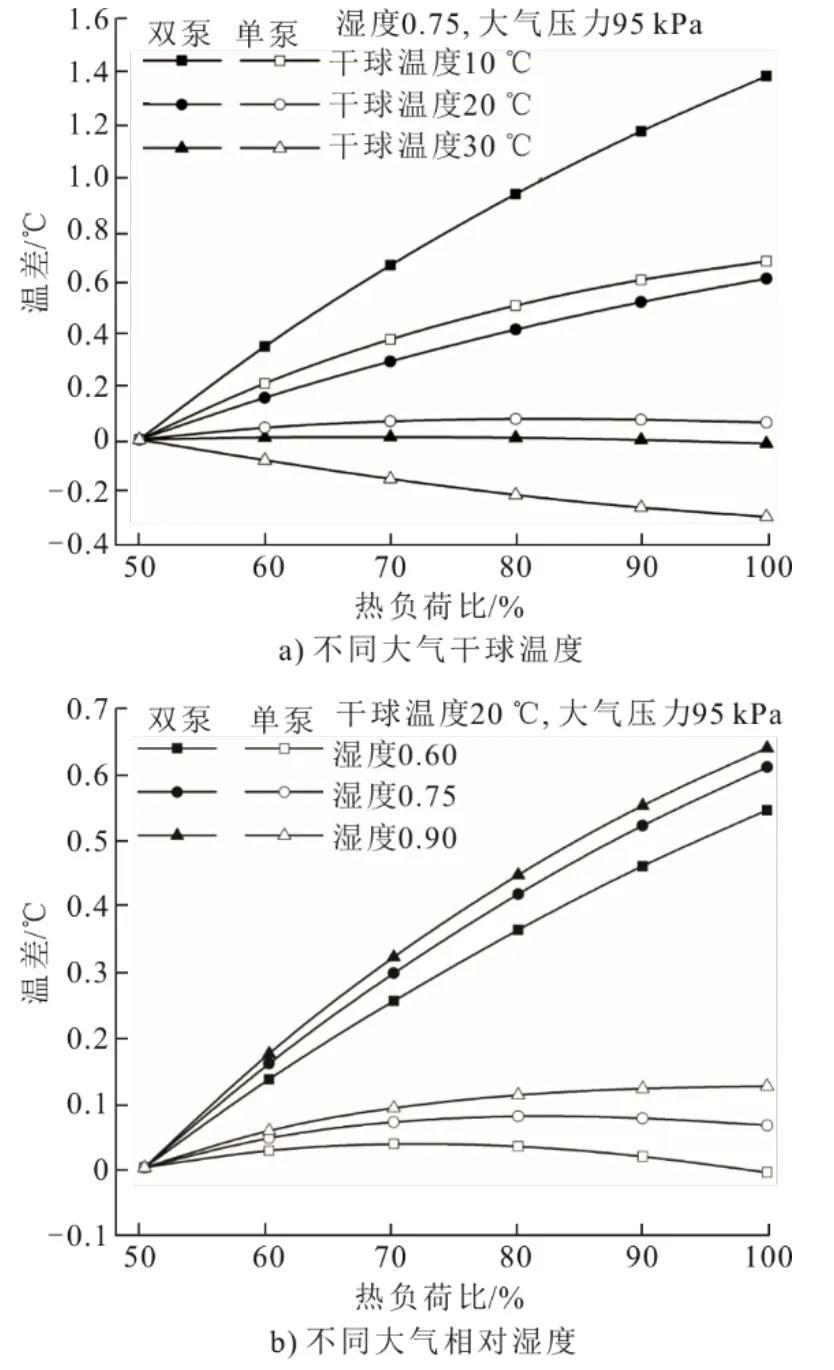
图5 冷却塔热负荷对出塔水温的影响Fig.5 Effect of heat load on CT outlet water temperature

相同循环水流量条件下，随着大气干球温度的升高，出塔水温随热负荷的升高先后呈升高、基本不变、降低的变化趋势，存在一临界干球温度值使热负荷对出塔水温基本没有影响，对于一机一泵和一机两泵工况，这一临界值分别约为20、30 ℃（图5a)）。热负荷对出塔水温的影响还将随着相对湿度的变化而变化（图5b)）。考虑到当地大气相对湿度的变化通常为0.60～0.90，热负荷对出塔水温的影响受相对湿度的影响远小于干球温度和循环水流量的影响（图5）。

4.3 环境参数

大气干球温度和相对湿度对冷却塔出塔水温和冷却幅高的影响如图6所示。从图6 可以看出，冷却塔出塔水温和冷却幅高随着干球温度和相对湿度的增大分别呈升高和减小的变化趋势，且大气相对湿度对出塔水温和冷却幅高的影响随着干球温度的升高而增大。

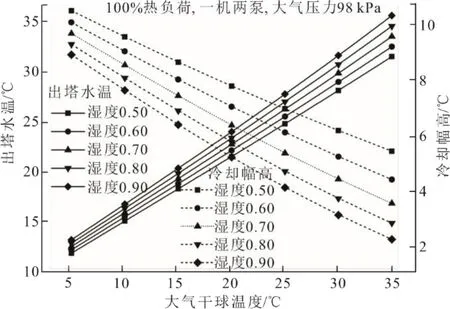
图6 干球温度和相对湿度对出塔水温和冷却幅高的影响Fig.6 Effects of dry bulb temperature and relative humidity on CT outlet water temperature and cooling approach

图7 为大气压力对冷却塔出塔水温和冷却幅高的影响。由图7 可以看出，不同干球温度下大气压力对冷却塔出塔水温和冷却幅高的影响均较小。当干球温度为30 ℃时，大气压力从95 kPa 升高至105 kPa，出塔水温仅升高0.2 ℃，冷却幅高仅增加0.1 ℃。考虑到一年四季中大气压力的变化幅度通常只有2～3 kPa，因而实际运行中可以忽略大气压力变化对出塔水温的影响。

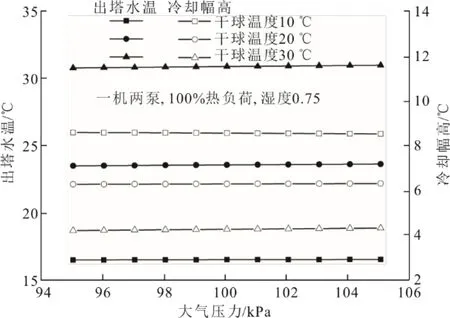
图7 大气压力对出塔水温和冷却幅高的影响Fig.7 Effects of atmospheric pressure on CT outlet water temperature and cooling approach

5 结论

1）本文拟合得到了雨区阻力系数的计算公式，可克服现有雨区阻力系数计算公式对淋水密度和填料层风速适用范围较小的弊端。

2）基于麦克尔焓差法建立了冷却塔一维热力计算模型，模型计算得到的出塔水温与试验实测结果相比最大偏差仅为1.6%。

3）出塔水温随着循环水流量的增大而升高，但循环水流量对出塔水温的影响将随着热负荷、大气干球温度和相对湿度的变化而变化；热负荷对出塔水温的影响受循环水流量、大气干球温度变化的影响较大，而受大气相对湿度变化的影响相对较小；出塔水温和冷却幅高随着大气干球温度和相对湿度的增大分别呈升高和减小的变化趋势，而大气压力的变化对出塔水温和冷却幅高的影响可忽略。