改进变指数趋近律直线伺服系统位置滑模控制

白喜强,崔皆凡,金少山

(沈阳工业大学 电气工程学院，辽宁 沈阳 110000)

0 引 言

近年来，永磁同步直线电机(PMSLM)得到了快速发展，尤其广泛应用于数控机床、数字化生产线等高精密的工业领域[1-2]。但直线电机直接带动负载运动，电机性能易受负载变化影响，且电机运行时会受参数变化以及一些非线性因素的影响，使得提高电机性能难度大。传统的 PID控制难以满足高性能控制的要求[3]。因此,需要设计一种控制器使系统具有较强的鲁棒性以及较高的响应速度。

滑模控制(SMC)本质上是一类特殊的非线性控制，其非线性表现为控制的不连续[4]。其结构简单，具有很强的鲁棒性，然而，在电机起动过程中SMC需要较长的时间才能使系统达到稳定状态，而且还存在抖振现象[5]。文献[6]采用加权积分增益与指数趋近律结合来减小抖振加快响应速度，但其抑制抖振效果不好。文献[7]设计了新的滑模趋近律，并且与模糊控制结合来减小滑模抖振，但其稳态时速度响应仍存在明显抖振。文献[8]采用线性矩阵不等式(LMI)来设计滑模等效控制律，并用扩张状态观测器(ESO)对各种干扰进行实时估计补偿，来增强系统鲁棒性。文献[9]通过对滑模趋近律进行改进以提高电机参数变化的鲁棒性。文献[10]在传统指数趋近律的基础上引入双曲正切函数、终端吸引子等来削弱抖振水平。

为了改善PMSLM的控制性能，减小滑模变结构控制引起的抖振问题。本文设计了基于ESO的改进变指数趋近律位置SMC。在传统指数趋近律的基础上，引入状态变量变指数积分幂次项、幂次趋近律和饱和函数,有效地减小滑模引起的抖振问题，提高了电机稳定性。引入了ESO，对外界负载扰动进行实时观测，增强系统鲁棒性。

1 PMSLM数学模型

基于d-q坐标系下PMSLM的数学模型：

ud=Rsid+pψd-ωψq

(1)

uq=Rsiq+pψq+ωψd

(2)

ψd=Ldid+ψf

(3)

ψq=Lqiq

(4)

式中：uq、ud为d、q轴电压;iq,id为d、q轴电流;ψq、ψd为d、q轴的励磁磁链；Lq、Ld为d、q轴电感；ω为电角速度；Rs为定子电阻；p为微分算子。

PMSLM电磁推力方程可表示为

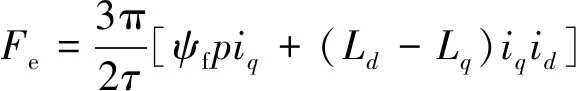
(5)

式中:τ为极距;p为极对数。对于表贴式PMSLMLd=Lq。

电磁推力表达式可以表示为

(6)

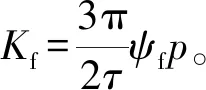
PMSLM机械运动方程可表示为

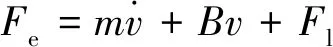
(7)

式中:m为动子质量;B为黏滞摩擦因数；Fl为广义负载扰动。

将式(6)代入式(7)可得：

(8)

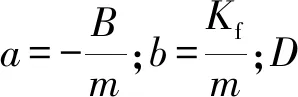
2 位置SMC设计

2.1 改进变指数趋近律

传统指数趋近律：

(9)

改进的变指数趋近律：

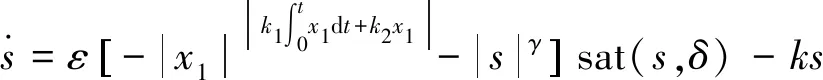
(10)

式中:k、k1、k2均为大于0的常数；0<γ<1；sat(s,δ)为饱和函数。

(11)

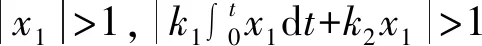
该趋近律充分结合幂次项和指数项的特点，在不同趋近阶段具有不同的快速趋近特性，较好地控制收敛速率。

2.2 改进SMC设计

为了实现对系统状态的完全跟踪，定义电机动子位置误差为控制器的状态变量：

x1=pf-p*

(12)

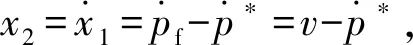
(13)

传统的滑模面函数中包含微分分量，容易引起系统抖振[11]，积分滑模面函数具有平滑推力、减小系统稳态误差、削弱抖振、增强控制器稳定性的良好品质，本次控制器设计采用积分滑模面：

(14)

其中,C0、C1>0。

结合式(10)、式(14)设计改进SMC，等效控制律设计为

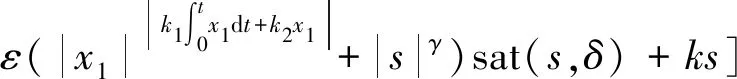
(15)

切换控制律为

(16)

与式(16)联立的控制律为

u=ueq+uvss=

khs+βhsat(s,δ)]

(17)

根据控制律所设计的SMC如图1所示。

图1 改进变指数趋近律SMC

构造李雅普诺夫函数:

(18)

对式(18)求导得：

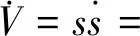
(19)

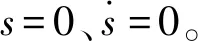
3 基于ESO的新型SMC设计

ESO实际上是通用的扰动观测器[12]，不依赖于系统的数学模型[13],可以实时估计控制系统的外界负载扰动,增强系统鲁棒性。

对于非线性系统：

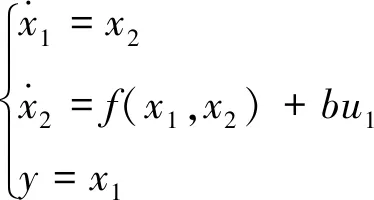
(20)

建立ESO：

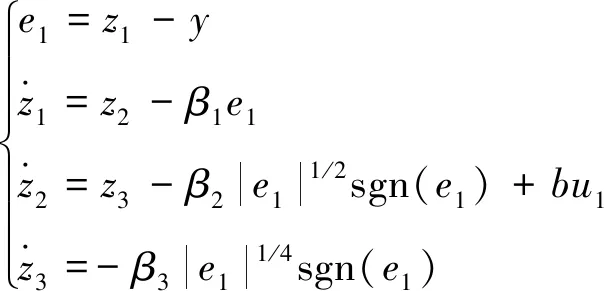
(21)

其中选择合适的β1、β2、β3的值，就可以很好地估计出x1、x2、x3[14]。即：

z1→x1、z2→x2、z3→x3

针对PMLSM的ESO：x1=pf、x2=v、u1=iq、z3为扰动观测值。

4 仿真分析

为了验证改进变指数趋近律积分SMC以及与ESO结合的控制效果，进行了仿真验证。所采用的电机参数如表1所示。

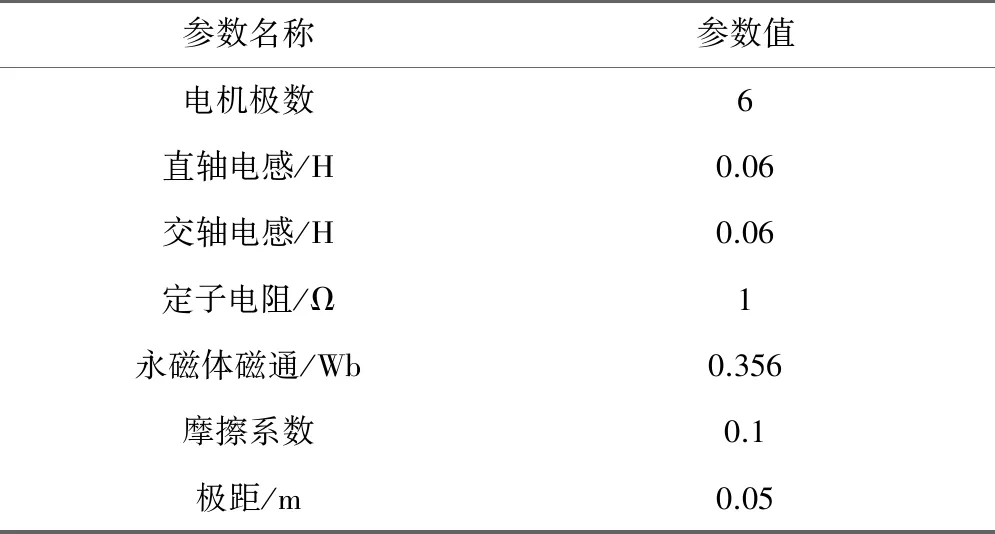
表1 PMLSM参数

针对上述电机，设计基于ESO的改进变指数趋近律SMC如图2所示。

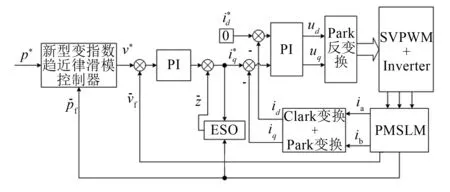
图2 PMSLM控制系统模型

仿真分别对电机进行了空载和突加负载仿真试验，电机线速度为1 m/s，仿真时间为0.5 s。改进SMC参数如表2所示。

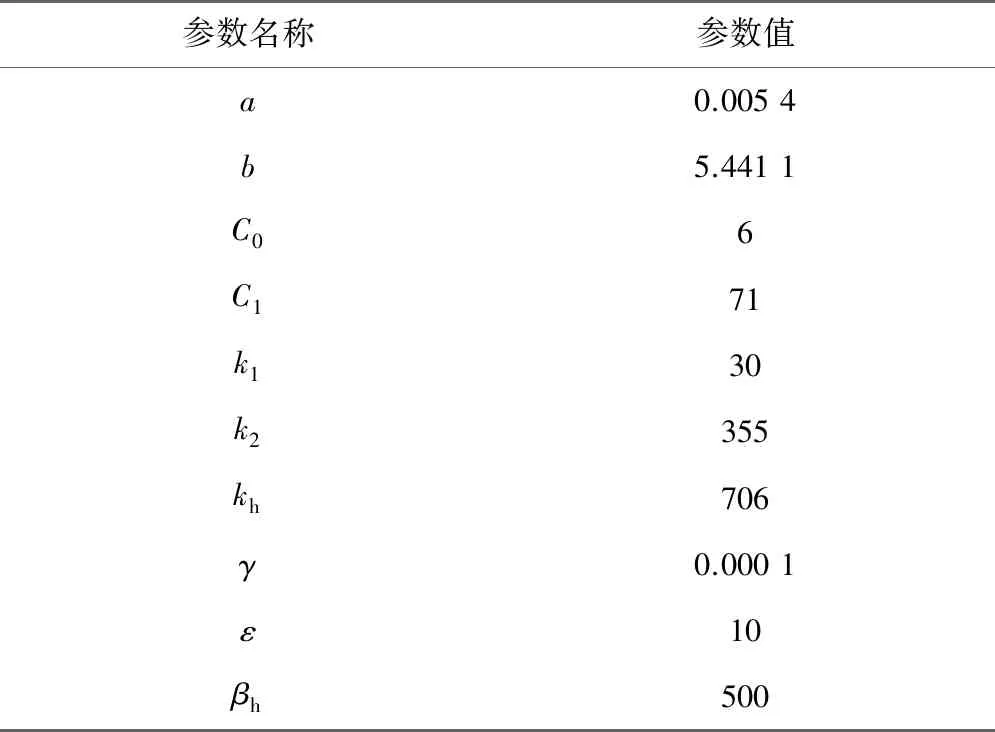
表2 改进SMC参数

根据图3所示的电机位置误差波形来看，改进变指数趋近律的SMC响应时间较短，减小了0.15 s。在系统达到稳态时，改进SMC抖振明显减小，且控制精度也有所提高，稳态时误差达到0.5 μm，而传统指数趋近律平均稳态误差在2 μm。

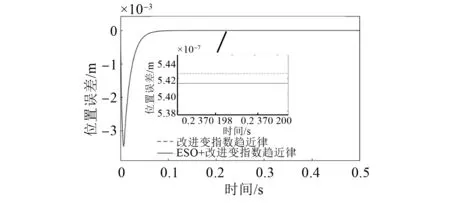
图3 位置误差波形

图4、图5分别为传统指数趋近律和改进变指数趋近律SMC的电机速度波形。从图5可以看出，改进后的SMC速度超调略大，但抖振现象明显减小。

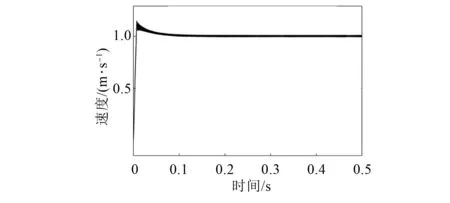
图4 传统指数趋近律SMC速度波形

图5 改进变指数趋近律SMC速度波形

图6、图7分别为2种控制方法空载时的q轴电流波形，从波形可以看出，0.08 s后，改进后的SMC的电机电流波动明显减小。

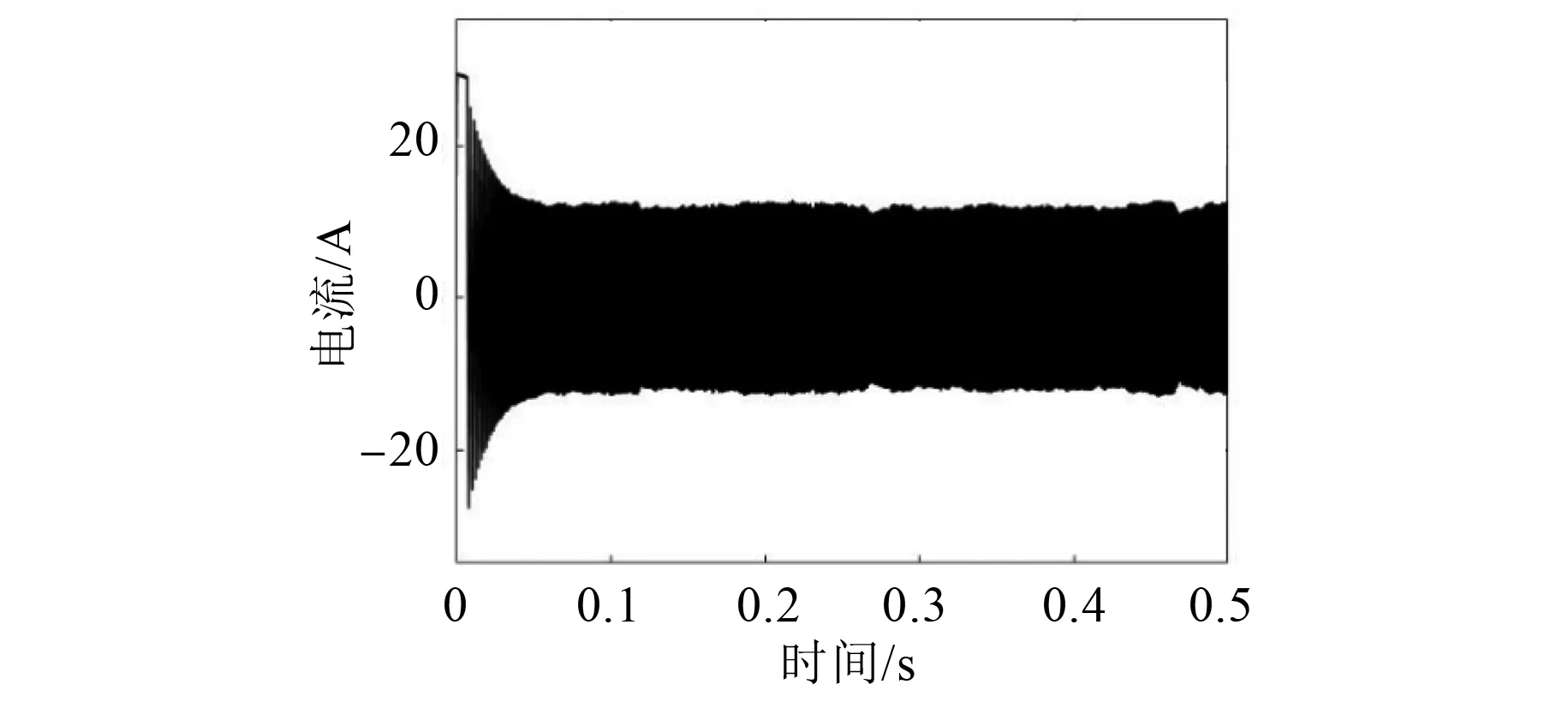
图6 传统指数趋近律SMC iq波形

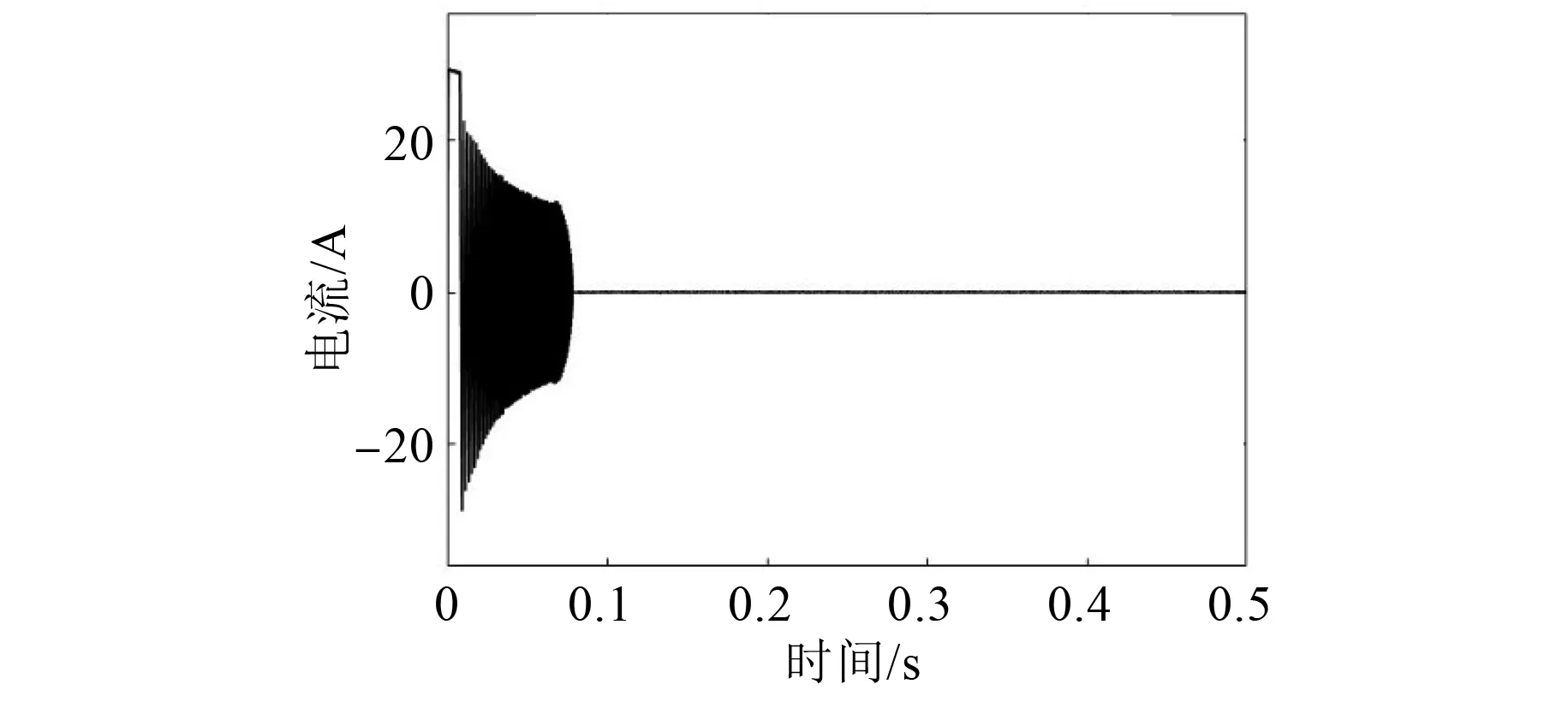
图7 改进变指数趋近律SMC iq波形

图8为控制系统有无ESO的电机位置误差波形对比图。加入ESO的控制系统稳态误差比未加入ESO的SMC系统减小了0.001 μm，可以看出ESO的观测误差对系统的跟踪误差几乎没有影响。在0.3 s突加100 N负载后，如图9所示，ESO可以使电机在突加负载后可以很快地回到突加负载前的状态，提高了电机系统的鲁棒性。

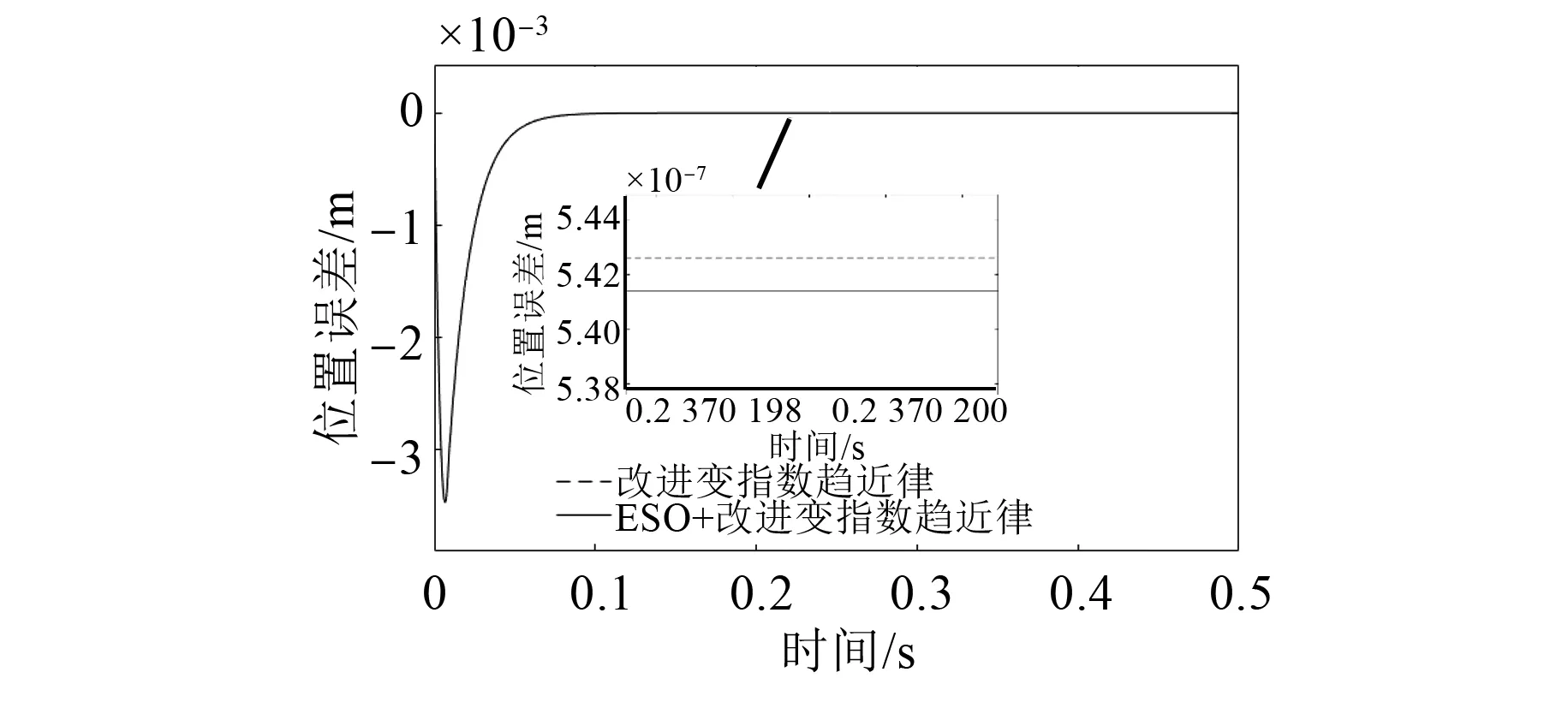
图8 位置误差波形

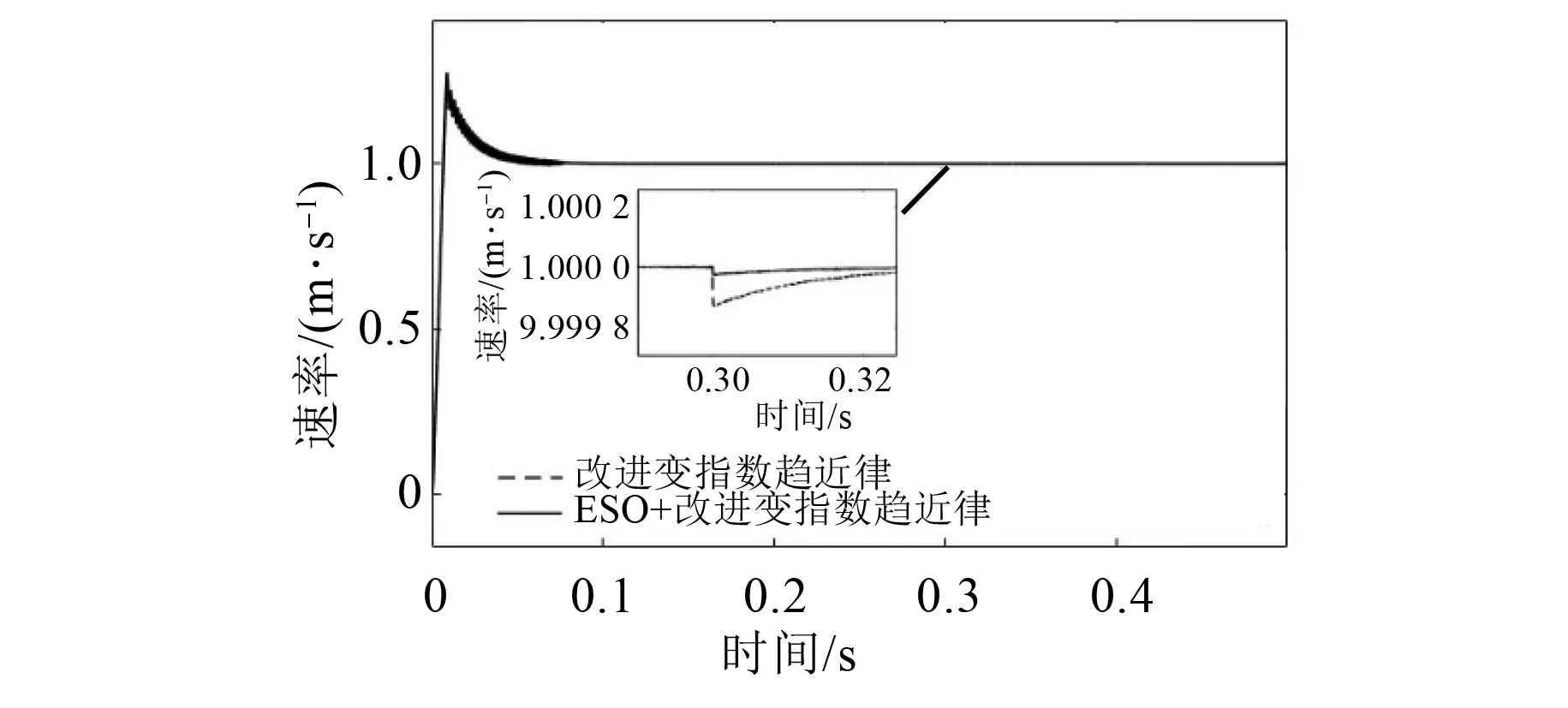
图9 电机速度波形

图10为改进后的SMC电机动子实际位置与给定位置的波形。可以看出，改进后的控制器可以使动子很好地跟随给定位置，电机的稳态误差从2 μm减小到0.5 μm。

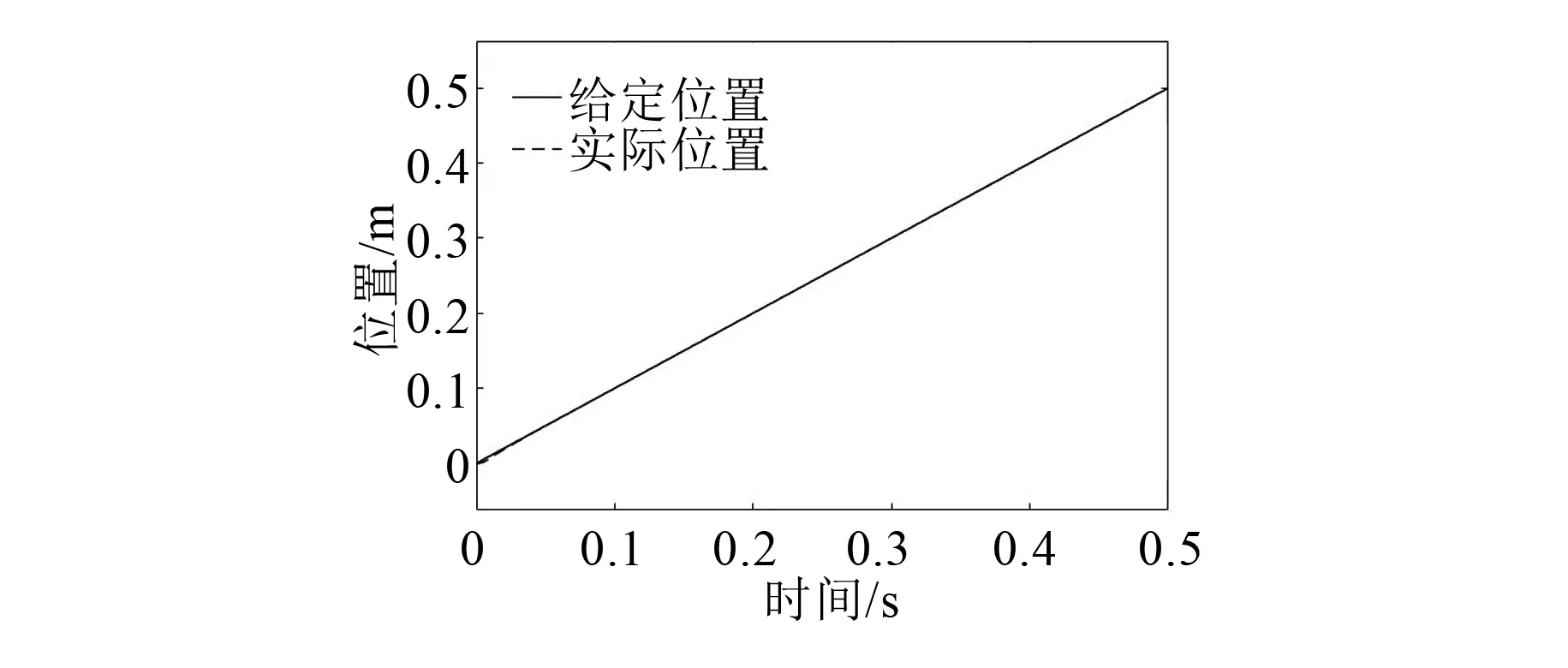
图10 动子实际位置和给定位置波形

5 试验研究

为了验证基于ESO改进SMC的可行性，搭建了电机试验平台,如图11所示。试验平台控制对象是圆筒型PMSLM，主控芯片是DSPTMS320F28335。试验平台以DSP28335为核心控制单元，系统主要硬件包括电源电路、控制电路、功率驱动电路、故障检测、信号检测电路和保护电路以及通信电路。

图11 PMLSM控制系统试验装置

电机设定速度为1 m/s，运动行程为0.3 m。图12、图13分别为改进前后电机的位置误差波形。可知，改进后的SMC响应时间更短，约为0.08 s，且跟踪误差也较小。

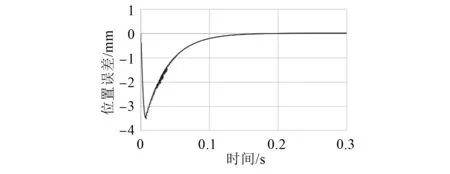
图12 传统指数趋近律SMC位置误差波形

图13 改进SMC位置误差波形

图14、图15分别为改进前后电机的速度波形。可知，改进后的滑模抖振明显减小。图16为基于ESO改进SMC电机动子的实际位置波形，试验结果符合仿真分析结果。

图14 传统指数趋近律SMC速度波形

图15 改进SMC速度波形

图16 动子实际位置波形

6 结 语

为了提升PMLSM控制性能，本文提出了基于ESO改进的变指数趋近律SMC。在指数趋近律的基础上引入状态变量的变指数积分幂次项、幂次趋近律和饱和函数，同时引入ESO来增强系统鲁棒性。通过与传统的指数趋近律SMC进行对比，改进后的SMC可以明显地抑制滑模本身存在的抖振问题，控制精度也明显提高，系统鲁棒性也明显增强，并通过仿真与试验进行了验证。