单相NPC型H桥级联逆变器电容电压不均与环流相互作用机理及建模研究*
2021-10-26吕敬高朱俊杰原景鑫
吕敬高,朱俊杰,原景鑫
(1.海军驻湖南地区军事代表室,湖南 湘潭 411101,2.海军工程大学 舰船综合电力技术国防科技重点实验室,湖北 武汉 430033)
0 引 言
近年来,多电平逆变器在大功率交流传动、新能源供电、轨道交通等领域应用越来越广泛[1-3]。与其他多电平逆变器相比,单相NPC型H桥级联逆变器具有级联灵活、结构便于扩展等优点,在中高压电能变换场合应用广泛[4-6]。
目前较多文献[1,7-11]对NPC型逆变器的均压问题进行了深入研究,均压调制方法主要分为SPWM调制均压和SVPWM调制均压。文献[9]研究了单相NPC型H桥逆变器的调制均压方法,采用电压电流双闭环控制,将直流侧电容电压差引入电流预测控制实现均压。文献[10-11]通过编码轮换技术实现级联单元内部均压和各逆变器之间输出功率均衡控制,实现了较好的均压效果,同时减少了运算量。文献[12]采用两矢量三段式合成参考矢量,利用冗余矢量对中点电位的不同作用进行均压滞环控制,取得了良好的均压效果。文献[13]对基于脉冲跳变SVPWM的电压不均影响因素进行了定量分析,建立了综合多因素的电压不均数学模型。但是没有分析多台逆变器并联环流对电压不均的影响。
很多文献对逆变器的环流抑制进行了深入研究。文献[14-16]根据激励源的不同,对环流进行分类,针对不同类型的环流采用不同的抑制策略,但是采用硬件方法抑制高频环流会导致系统体积增大。文献[17]提出的改进19矢量法,利用19个矢量进行参考矢量合成,但采用的矢量合成方法是5段式,存在输出电压谐波含量高的问题。文献[18]提出基于PIR控制器的环流控制方法,能够有效改善环流低频分量的控制能力,但当参考电流不相等时,环流会产生尖峰脉动。为了消除尖峰脉动,文献[19]采用“PIR+前馈+双采样”的方法控制小矢量作用时间来抑制零序环流,取得了较好的环流抑制效果。
虽然上述文献对NPC型逆变器的均压控制和多电平逆变器的环流抑制进行了研究,但是对电容电压与环流之间的相互作用机理研究则较少。对于单相NPC型H桥级联逆变器并联系统而言,环流会影响逆变器的输出电流,进而对电容电压不均造成影响,而逆变器之间的电容电压不均差异会造成逆变器端口输出电压不一致,进而产生环流,因此需要明确环流与电容电压不均的相互作用机理,定量分析环流与电容电压不均的关系,建立环流对电容电压不均影响的数学模型。为此本文以一个控制周期为时间单位,推导了环流与电容电压不均之间的相互关系。分析了周期稳态运行时环流对电容电压不均的作用,建立了基于阻滞增长的环流作用模型,为环流作用下的电容电压不均值预估提供了理论依据。
1 单相NPC型H桥级联逆变器并联拓扑结构
图1为单相NPC型H桥级联逆变器并联拓扑结构,它由两个完全相同的单相NPC型H桥级联逆变器A和B、电压相等的恒压源UH1和UH2以及RL负载构成。每个单相NPC型H桥逆变器由桥臂a、b、c、d、支撑电容C1、C2、C3、C4构成,其中桥臂a、b与支撑电容C1、C2并联构成的H桥单元为CH1,桥臂c、d与支撑电容C3、C4并联构成的H桥单元为CH2,CH1和CH2通过桥臂b、c的中点级联构成了单相NPC型H桥级联逆变器,桥臂a、d的中点作为输出端口与负载连接。两台逆变器的并联方式为直流侧共用恒压源UH1和UH2,交流侧输出并联在RL负载上。逆变器A和B的两个输出端口线路阻抗分别为ZA1、ZA2、ZB1、ZB2,RL负载的阻抗为Z,逆变器A和B的输出电流分别为iLA和iLB,流经RL负载的电流为iL1。

图1 单相NPC型H桥级联逆变器并联拓扑结构
为了便于对两台逆变器并联环流的定量分析,给出一个开关周期单台逆变器的电容电压不均和输出电压表达式。
定义桥臂的状态下

(1)
式中:Sxi(x=a,b,c,d;i=1,2,3,4)为1表示功率器件导通;Sxi为0表示功率器件关断。
由于调制算法、死区等因素影响,单相NPC型H桥级联逆变器中的支撑电容C1、C2、C3、C4的电压值存在不均。对于单台逆变器,一个开关周期内CH1和CH2的电容电压不均表达式为[14]

(2)
式中:下标k表示第k个矢量作用,Svk=Sak-Sbk+Sck-Sdk;ΔUh1表示上H桥电容电压不均;ΔUh2表示下H桥电容电压不均;iL1k表示第k个矢量作用时的负载电流;Δtk表示第k个矢量的作用时间,sign(x)符号函数定义为

逆变器输出电压uo表示为
uo=SaUC1-SbUC2+ScUC3-SdUC4
(3)
式中:UC1、UC2、UC3、UC4分别为支撑电容C1、C2、C3、C4的电压值;Sa、Sb、Sc、Sd分别为式(1)定义的桥臂状态。
根据叠加原理,逆变器实际输出电压uo可以等效为2个分量叠加:(1)电容电压完全均衡的理想情况下,逆变器的输出电压uo1;(2)电容电压不均等效电容电压源ΔUh1引起的逆变器输出电压uo2。为了实现直流侧按不同电压源进行等效分量分离,定义如下变量:

(4)
令St1=Sa+Sb,Sd1=Sa-Sb,St2=Sc+Sd,Sd2=Sc-Sd,式(3)可进一步表示为
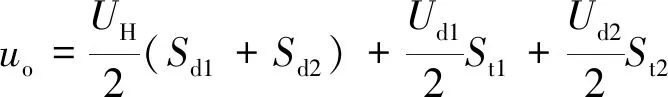
(5)
式中:UH/2为不存在电容电压不均,理想情况下的电压值,等效为恒压源电压值;Ud1/2和Ud2/2分别为CH1和CH2的支撑电容电压不均值。
2 基于开关周期的电容电压不均与环流的关系
定性分析来看,环流会影响单台逆变器的输出电流iL,进而对电容电压不均造成影响,而两台逆变器电容电压不均差异会导致逆变器的输出电流不同,从而产生环流,因此环流和电容电压不均之间存在相互作用关系。
2.1 电容电压不均对环流的影响
图2为两台逆变器并联等效电路,定义两台并联逆变器的环流为
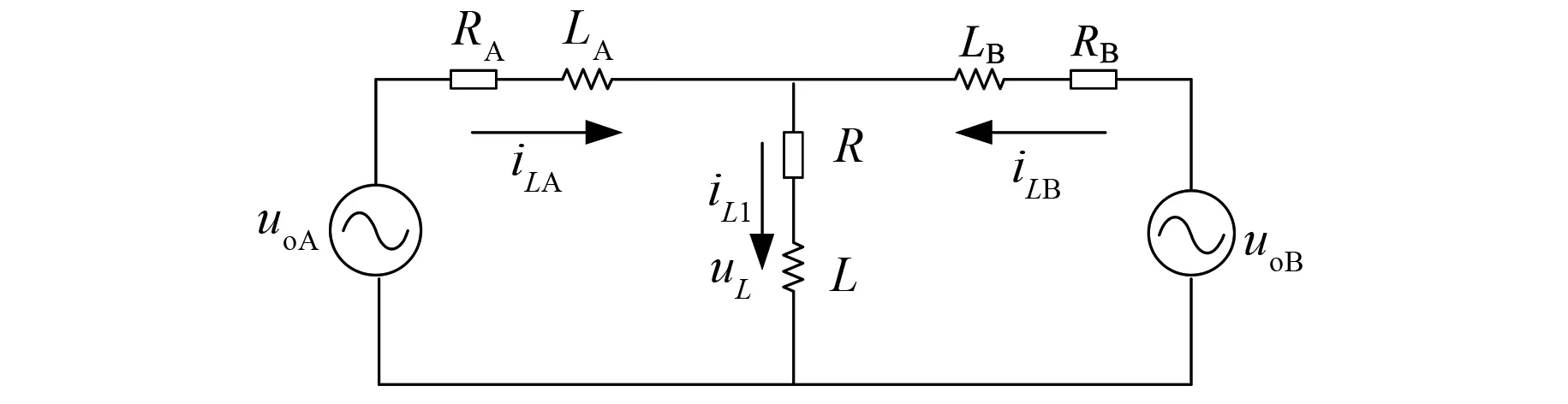
图2 2台单相逆变器并联等效电路图

(6)
根据基尔霍夫电压定律,得环流ih的表达式为

(7)
式中:uoA和uoB分别表示逆变器A和B的输出电压;ZA、ZB、Z分别表示逆变器A和B的线路阻抗和负载阻抗。
将式(5)代入式(7)可得到环流表达式为
ih=

(8)
记SA=(SaA,SbA,ScA,SdA),SB=(SaB,SbB,ScB,SdB),式中下标A表示逆变器A的相关变量,下标B表示逆变器B的相关变量。
可以看出,环流与线路阻抗、开关矢量、电容电压不均、恒压源电压大小有关,当ZA=ZB,SA=SB且UdA≠UdB时,电容电压不均对环流的表达式为
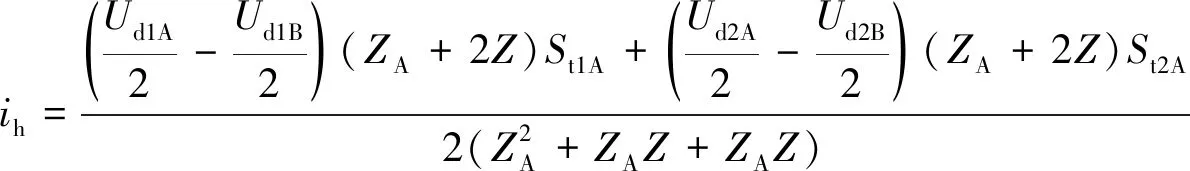
(9)
式(9)表明,环流激励源是 (Ud1A-Ud1B)/2和(Ud2A-Ud2B)/2。这说明即使并联逆变器线路阻抗相同,开关器件动作完全一致,并联逆变器电容电压不均差异也会产生环流。
2.2 环流对电容电压不均的影响
为了方便描述各电流之间的相互关系,根据叠加原理,进行如下变量定义:

(10)
逆变器A和B的输出电流表示为

(11)
式(11)表明,各并联逆变器的输出电流由两个电流分量叠加而成:(1)各逆变器均分负载电流iL1/2;(2)环流id/2,因此环流的作用相当于在均分负载电流上进行了线性叠加,结合式(2),可得引起逆变器电容电压不均的电流ic表达式:
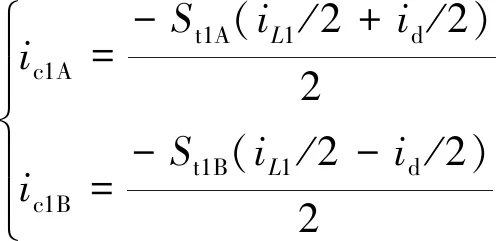
(12)
式中:St1A为A逆变器Sa+Sb的状态;St1B为B逆变器Sa+Sb的状态。
因此,受环流影响时,一个开关周期内逆变器A和B的CH1电容电压不均表达式分别为
ΔUh1(n)=

(13)
ΔUh2(n)=
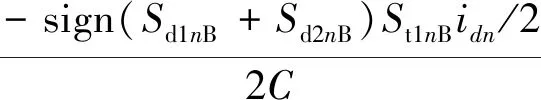
(14)
式中:下标n表示第n个采样周期;A表示逆变器A有关的状态量;B表示逆变器B有关的状态量;id和iL1的定义如式(10)所示。
环流作用下,CH2的电容电压不均表达式与式(13)、式(14)类似,不再赘述。可以看出,与单台逆变器工作的电压不均表达式式(2)相比,环流作用下的电容电压不均表达式增加了环流分量引起的电压不均。对于一个具体的控制周期,由于逆变器A和逆变器B的环流相位相反,环流的作用表现为,减小一台逆变器的电容电压不均,同时增大另外一台逆变器的电容电压不均,且作用程度由环流大小决定。
为了进一步从物理概念的角度对环流的作用进行说明,图3给出了矢量SA=SB=(1,-1,0,-1)作用时的环流路径,假设环流从逆变器A流向逆变器B,虽然存在2条环流路径,但经过Sa1的环流不流过电容,而经过Sb3、Sc2的环流流过电容C4,造成C4B充电,C4A放电。

图3 2台单相逆变器并联环流路径
通过分析逆变器的等效电路,可以得到:当iL1<0时,开关矢量(1,-1,0,-1)对C4充电,叠加了环流的作用后,C4B充电作用更明显,而C4A的充电作用被减弱,意味着(1,-1,0,-1)对逆变器A的均压调节能力加强,逆变器B的调节能力减弱;同理,当iL1>0时,逆变器A的均压调节能力减弱,逆变器B的调节能力加强。
综上所述,环流和电容电压不均的关系为:电容电压不均差异是环流的激励源之一,即使逆变器的线路阻抗和开关动作完全相同,如果两台逆变器的电容电压不均存在差异,也会产生环流;对于一个控制周期,环流会改善一台并联逆变器的电容电压不均,同时恶化另一台逆变器的电容电压不均。
3 稳态阻滞增长的环流作用模型
根据式(8),逆变器并联环流产生的因素有很多,为了简化分析,只研究由输出线路阻抗差异产生的环流对电容均压的影响。假设两台逆变器的输出阻抗不平衡系数为n,且满足ZB=nZA(n≥1),两台并联逆变器采用主从控制,忽略通信延迟造成的开关动作差异。
对于每一个控制周期,环流会造成一台逆变器的矢量均压调节能力增强,另一台调节能力减弱。但对整个运行过程中的均压效果而言,环流对均压的作用效果受以下因素的影响:(1)环流的大小;(2)运行过程中St≠ 0的作用时间;(3)环流与负载电流的相位关系;(4)输出电压作用电平。直接分析一个基波周期中每一个控制周期的作用比较复杂,而且得到的模型适应性差,为此从宏观角度考虑环流对均压的数学模型。采用“假设—建模—求解—检验—校正”的思路进行环流建模,具体步骤如下:
(1)模型建立。根据式(13)和式(14),为了衡量由环流产生的电容电压不均大小,定义环流产生的电压不均Udih:

(15)
式中:下标i表示CHi的相关变量,由于ZB=nZA,(n≥1),运行时iLA≤iLB。
对逆变器A而言,环流产生的电容电压不均分量具有改善均压的作用,电容电压不均减小后环流分量的作用进一步减小,最终达到自平衡状态,因此均压算法对环流产生的电压不均作用较小,电容电压不均变化不明显。对逆变器B,由于环流和电容电压不均具有相互激励的作用,不能实现自平衡,电容电压不均受到均压算法的限制。根据第2节的分析可知,电容电压不均和环流相互影响,环流较小时,产生的电容电压不均分量较小,电容电压不均受环流影响不大,均压算法对其抑制作用较小;随着环流的增大,电容电压不均与环流的相互作用越来越明显,产生的电容电压不均越来越大,此时均压算法对环流分量产生的电压不均作用也在逐渐增强。但是二者的相互激励并不会使环流和电容电压不均无限增长,当环流达到一定程度时,由于产生的电容电压不均非常大,均压算法对其抑制作用达到最大,电容电压不均达到上限。这一变化过程与阻滞增长模型的变化规律十分类似,不妨先假设电容电压不均与环流的关系符合阻滞增长模型。
阻滞增长模型微分表达式为
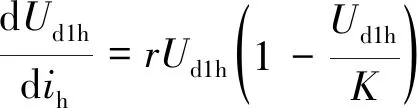
(16)
式中:K为均压算法容纳的电容电压不均最大值,大小与均压算法、电容大小等外部因素有关;r为电容电压不均增长率。
该函数的积分形式为

(17)
式中:a为积分常数,与无环流时的电容电压不均大小有关。
(2)参数求解。阻滞增长模型的参数主要有K、a、r,相关的求解方法有很多,本文采用文献[20]介绍的三点迭代法进行参数计算,计算公式如下:
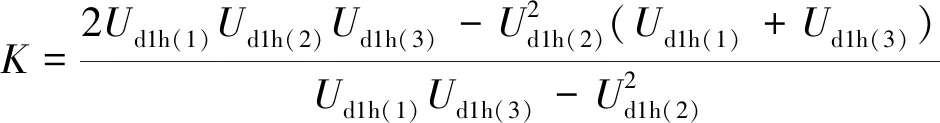
(18)
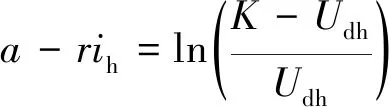
(19)
式中:Ud1h(1)、Ud1h(2)、Ud1h(3)分别表示环流起始点,中间点和终止点对应的电容电压不均值。
通过改变线路阻抗不均系数n,得到以ih/iL为横轴、Ud1h为纵轴的仿真数据点,利用式(18)和式(19)计算的参数值为K=54.48,a=247.7,r=3 389。
(3)模型检验。实际应用时,通过线路阻抗调整,一般将环流限定在负载电流的10%以内。为了研究环流对电容电压不均的变化规律,通过改变逆变器输出线路阻抗大小,仿真得到多组环流与电容电压不均的对应关系。
图4中曲线1、2分别为逆变器A、B的CH1电容电压不均随环流大小的变化曲线,曲线3为环流导致的电压不均Udih。可以看出,逆变器A的电容电压不均基本保持不变,这是由于环流具有自平衡作用;逆变器B的电容电压不均随环流发生变化,而且当环流为7%左右时发生突变,曲线3的变化趋势与曲线2的变化趋势基本一致,说明环流对逆变器A的电容电压不均影响比较小。由于逆变器A、B采用主从控制,即使不存在环流,2台逆变器的电容电压之间也会存在固有的中点电位差。采用式(17)的阻滞模型对曲线3进行数据拟合,得到拟合结果为曲线4。可以看出,曲线4在环流较小的部分拟合较差,数据点与计算值存在零偏;在7%后的部分能基本反映电容电压不均的变化趋势,但数据点存在波动现象,计算值的精度有待提高。

图4 环流对电容电压不均的影响曲线
(4)模型修正。针对图4所示的模型误差,对阻滞模型进行修正,在阻滞模型的基础上加入幅值补偿系数实现对环流较小的部分进行平移,同时为了反映环流对电容电压不均的波动影响,加入正弦波动分量提高拟合精度。
修正后的电容电压不均Ud1h表达式为

(20)
式中:k·ih+b为线性幅值补偿;c为波动分量幅值系数;ωh为波动角频率;d为波动相位系数。
采用非线性最小二乘法对式(20)进行参数估计,得到最优参数取值:(K,a,r,k,b,c,ωh,d)=(22.9,1 735,2 378,245.9,9.709,1.756,286,3.354),模型校正后的电容电压不均与环流关系拟合曲线如图5所示。可以看出,拟合曲线较好地反映了电压不均的变化趋势。

图5 模型校正后的拟合曲线
为了定量分析模型的拟合程度,采用拟合决定系数R2对拟合的效果进行评估,R2的表达式为
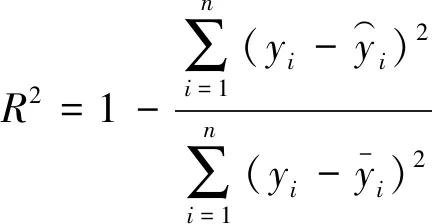
(21)

含有正弦分量和线性分量的阻滞修正模型能比较准确地描述环流对电容电压不均的作用,阻滞模型反映了均压算法对电容电压不均存在容纳上限。在环流作用的初期,由于产生的电容电压不均量较小,均压算法对其抑制作用不明显,电容电压线性增长,同时带有一定的波动性;当环流增大到拐点时,电容电压不均进入加速增长区,均压算法对电容电压不均的调节能力逐渐增强;当均压算法的调节能力等于电容电压不均增长能力时,随着环流的增加,电容电压不均增速受到均压算法限制,电容电压不均达到上限值。
4 仿真及试验验证
4.1 仿真验证
为了验证环流模型的正确性,首先对单台逆变器的调制算法进行验证,基于MATLAB/Simulink建立单相NPC型H桥级联逆变器仿真模型,调制算法采用文献[13]提出的脉冲跳变SVPWM滞环均压算法。主要仿真参数如表1所示。逆变器输出电压和电流波形如图6所示。可以看出,调制算法能输出稳定的单相电流波形和九电平电压波形,图7为直流侧电容电压波形,电容电压不均在200 V的范围内波动,说明均压算法能均衡直流侧的电容电压。单台逆变器能实现均压逆变的功能,为两台逆变器的并联实验奠定了基础。

表1 主要仿真参数
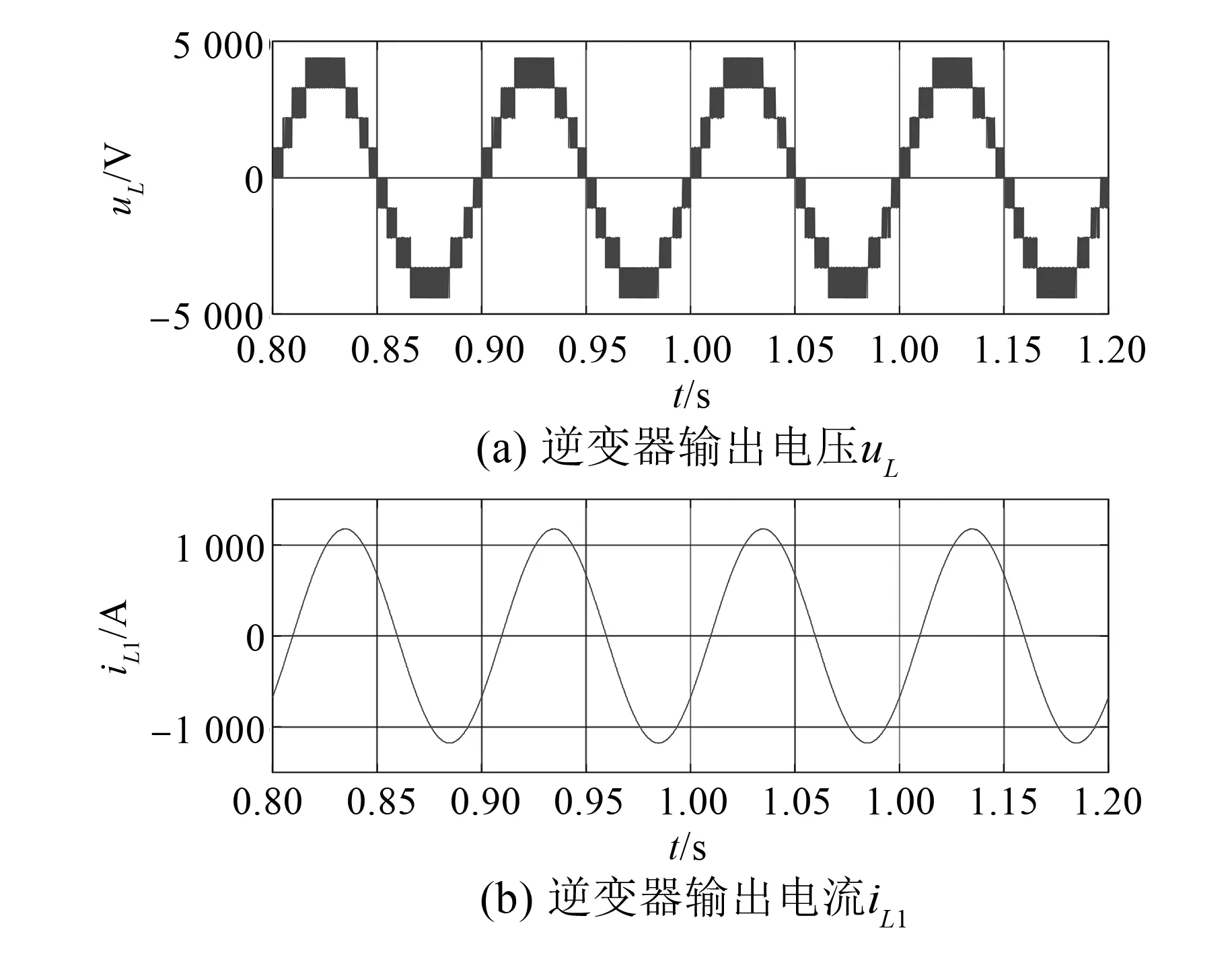
图6 单相NPC型H桥级联逆变器输出电压和电流波形

图7 直流母线电容电压波形
4.2 环流阻滞模型试验验证
为了验证环流阻滞模型的正确性,搭建了单相NPC型H桥级联逆变器试验平台,控制器采用DSP28335+FPGA的控制架构,其中DSP用来计算作用矢量和作用时间,FPGA发出对应的脉冲。
并联主从控制的脉冲延时约为十几微秒,对环流的影响非常小,因此线路阻抗大小不同是产生环流的主要因素。图8为两台逆变器并联时逆变器输出电流及对应的环流波形。
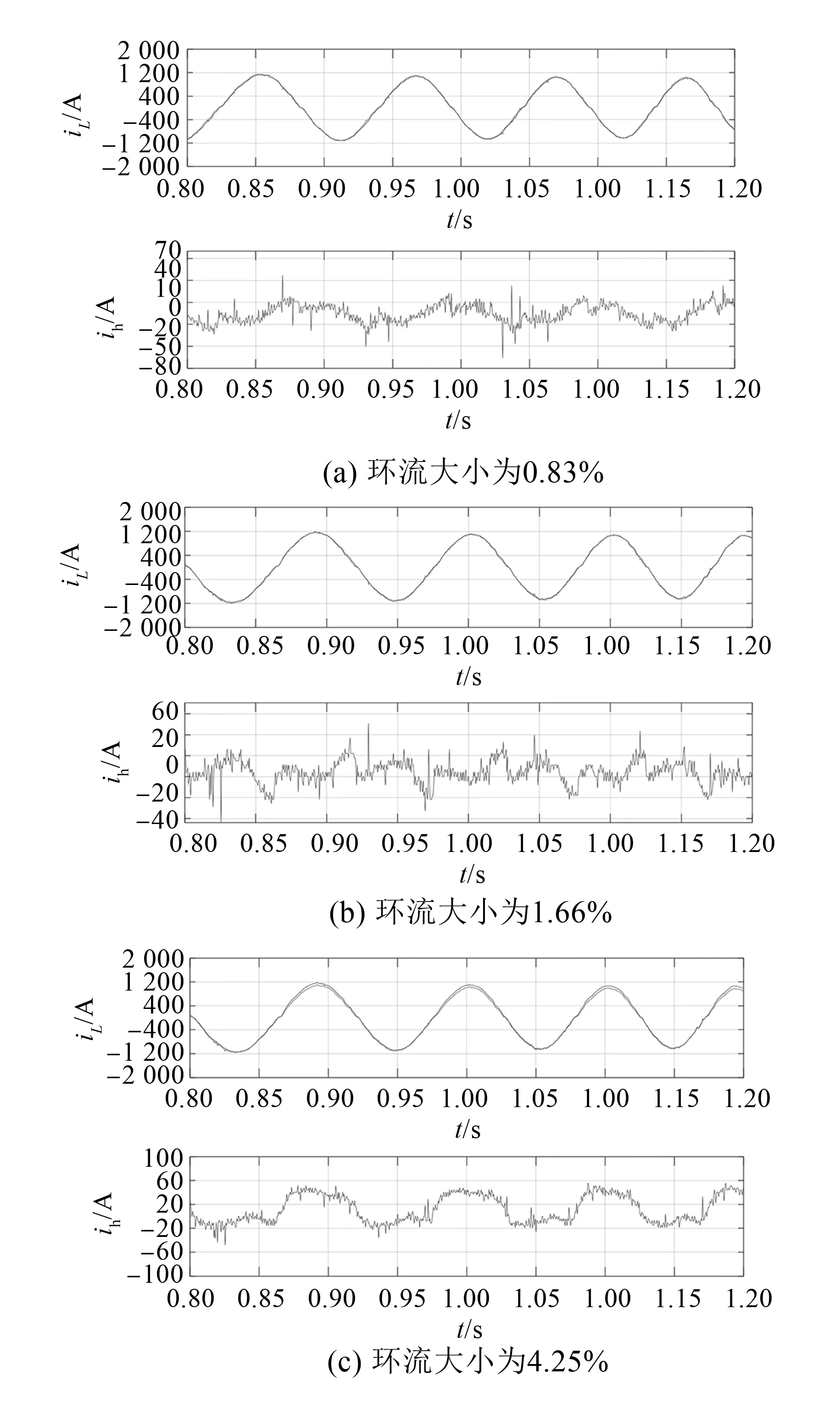
图8 逆变器负载电流与环流
为了产生指定大小的环流,进一步在RT-Lab试验平台上进行环流试验。通过改变逆变器A、B的线路阻抗不均系数k,产生预定的环流,测量得到的环流与电容电压不均如图9所示,环流阻滞模型计算的理论值与试验值的拟合决定系数为0.945,说明环流阻滞模型能较好反映环流对电容电压不均的作用。
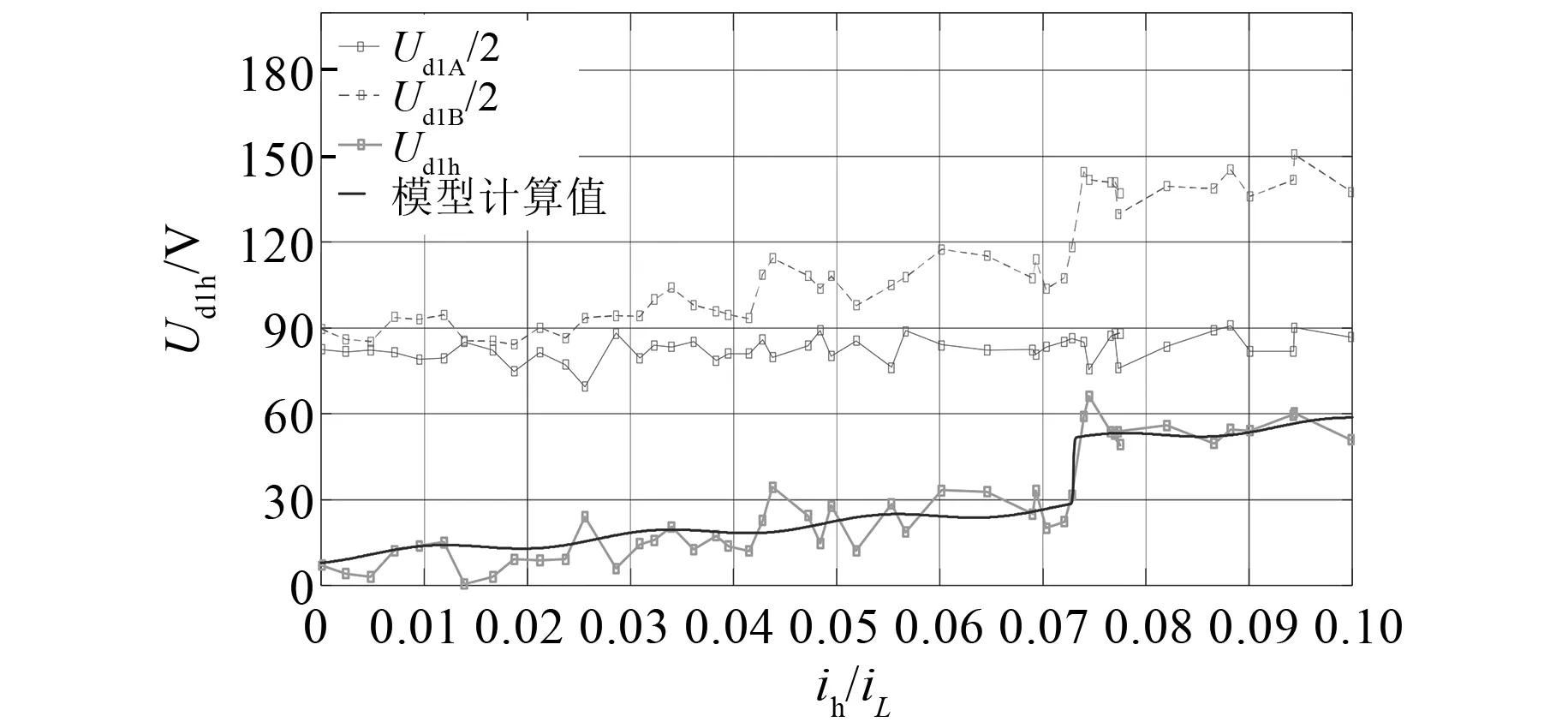
图9 电容电压不均与环流关系
5 结 语
本文对两台单相NPC型H桥级联逆变器的并联环流进行了研究,主要创新点如下:
(1)定量分析了一个开关周期内环流与电容电压不均的相互关系,即:电容电压不均差异是环流的激励源之一,两台逆变器的电容电压不均存在差异会产生均压环流;对于一个控制周期,环流会改善一台并联逆变器的电容电压不均,同时恶化另一台逆变器的电容电压不均。
(2)建立了稳态环流阻滞模型。采用“假设—建模—求解—检验—校正”的思路进行环流建模,避免了多因素建模的复杂过程,并通过仿真和试验验证了模型的准确性,仿真得到的模型拟合决定系数为0.963 8,试验得到的模型拟合决定系数为0.945 0。该模型为环流大小下的电容电压不均预估提供了理论依据。
