基于形态学的贯通式同相AT牵引供电系统牵引网单端电流方向暂态保护*

高敬业,杨鸿雁,蔡 潇,毕贵红,杨 毅,陈仕龙

(1.昆明理工大学 电力工程学院，云南 昆明 650500；2.云南电网有限责任公司电力科学研究院，云南 昆明 650217)

0 引 言

基于全线贯通技术和同相补偿技术的新型贯通式同相牵引供电系统，彻底解决了牵引供电系统中最为严重的过分相问题和负序问题，并大幅度提高了牵引供电系统的效率[1-3]。牵引供电系统的运行状态受内外诸多因素的影响，事故发生率高[4]。故障暂态电流信号中含有的故障信息比故障暂态电压信号更丰富，因此进一步研究由故障电流信号构成的牵引网暂态保护具有重要意义。由于自耦变压器(AT)供电方式具有通信防护效果好、牵引网供电距离长及牵引网损耗低等优点，目前高速重载铁路大部分选择该供电方式为机车供电，故本文选取贯通式同相AT牵引供电系统作为对象展开研究[5]。

数学形态学是一种处理非线性问题的方法，该方法不仅有速度快、时延小等优点，而且通过形态学处理故障暂态信号不会出现幅度衰减及相位移的问题。形态谱运算由开运算和闭运算组成，可提取故障暂态信号的形态谱，进而得到形态谱值。多分辨形态梯度(MMG)能可靠判断故障暂态电流信号波形突变点的极性，由此可以构成方向起动元件的判据[6]。

牵引变电所出口处电容和区外一段接触线共同构成贯通式同相牵引供电系统牵引网的天然边界，且该边界对高频分量具有较强的衰减作用[7]。通过结合牵引网边界对高频分量较强的衰减作用和数学形态学处理故障暂态信号的优点，提出了基于形态学的贯通式同相AT牵引供电系统牵引网单端电流方向暂态保护方法。通过MMG判断故障电流线模分量波形突变点极性的正负，若极性为负，则判别为本侧区外故障。若极性为正，则通过形态谱运算得到故障电流线模分量的形态谱，对该形态谱进行归一化并将其变换到频域，并将频域中形态谱值与阈值的大小进行比较，来判断区内故障、对侧区外故障。通过大量仿真，验证了该保护方法的可靠性和可行性。

1 贯通式同相AT牵引供电系统牵引网单端电流方向保护原理

1.1 贯通式同相AT牵引供电系统

贯通式同相AT牵引供电系统结构如图1所示。公共电网侧输入三相交流电流，通过三相PWM整流与单相PWM逆变将三相交流电变换为单相交流电，再通过单相升压变压器升压后进入牵引网，为电力机车的运行提供电能。

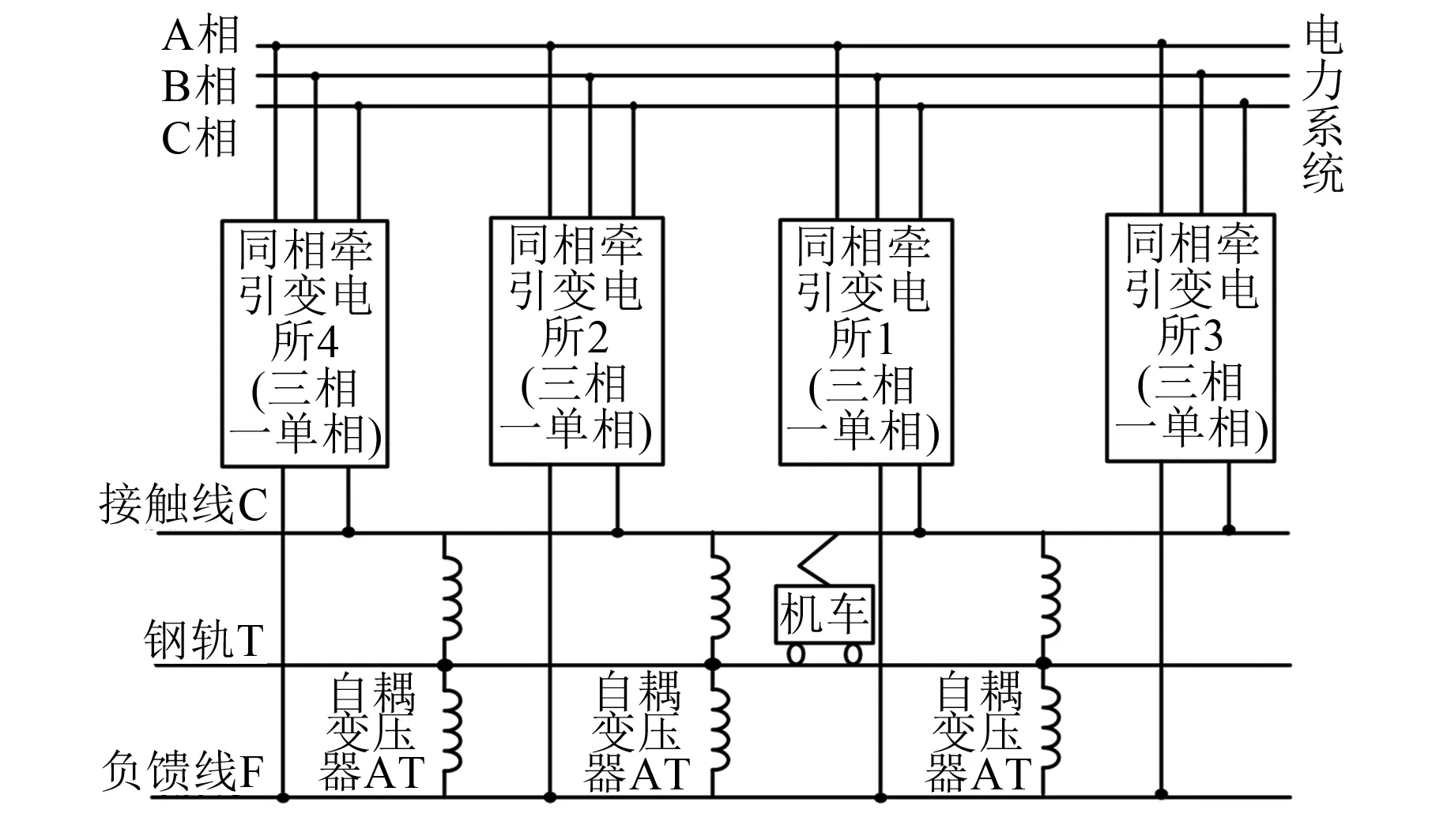
图1 贯通式同相AT牵引供电系统示意图

根据牵引网各导线的参数，由Carson理论可计算出牵引网阻抗Z的相量矩阵Z相、电感L的相量矩阵L相、电容C的相量矩阵C相，如下[8]：

(1)

(2)

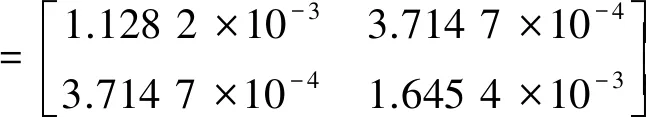
(3)

式中：Z相、L相、C相的单位分别为Z/km、F/km、H/km。

将贯通式同相AT牵引供电系统的牵引网简化为由C相和F相构成的两相不换位线路[9]。由于C相是由接触线与承力索2条相异的导线共同构成的一相二分裂导线，F相为负馈线、钢轨和回流线等效合并而成，C相和F相的线路参数不同，故牵引网是不对称线路。牵引网的不对称性导致线路的传播模量也是不平衡的，因此需要不同的变换矩阵对电压、电流波动方程进行对角化。电流、电压的相模变换矩阵为[8]

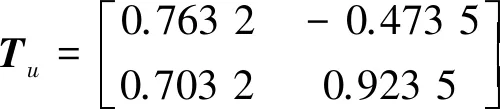
(4)

设有：

(5)

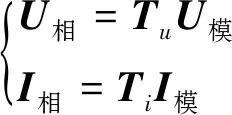
(6)

经计算可得

(7)

则

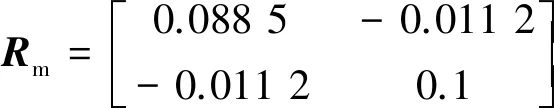
(8)

Lm=

(9)

(10)

式中：Rm、Lm、Cm分别表示牵引网电阻R、电感L、电容C的模量矩阵，单位分别是Ω/km、H/km、F/km。

由于牵引网电能质量易受交-直-交变换器所生成高次谐波的影响，可通过装设电容电感滤波装置来降低高次谐波干扰，该电容并联在牵引网上，其在牵引网中的连接方式如图2所示[10]。

图2 电容与牵引网并联示意图

文献[11]分析表明，3 m长接触线与牵引变电所出口处电容构成的牵引网边界可以用于判别区内和区外故障。牵引变电所出口处电容与区外3 m长接触线共同构成的牵引网边界的等效电路如图3所示。

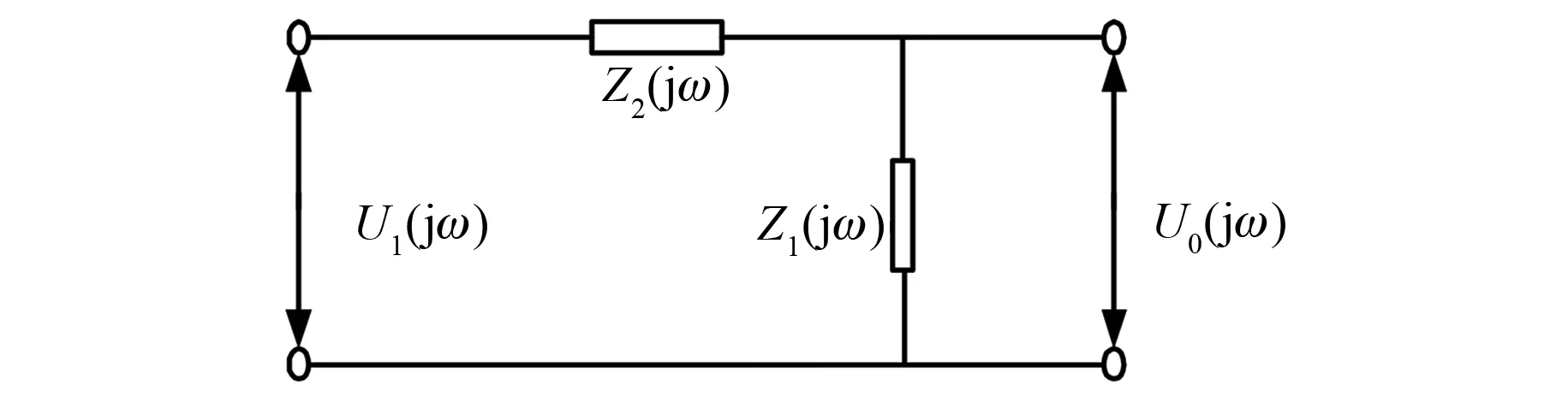
图3 牵引网边界等效电路

图3中，Z1(jω)为牵引变电所出口处电容的等效阻抗，Z2(jω)为3 m长接触线的等效阻抗。由图3推导出牵引网边界的传递函数G(jω)为

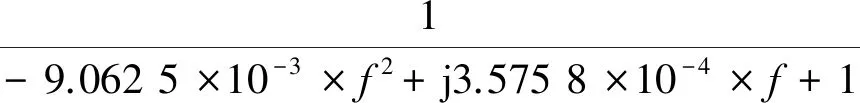
(11)

传递函数的幅频特性如图4所示。

图4 牵引网边界传递函数的幅频特性

由图4可知，低频部分传递函数的幅值接近于1；当频率f>1 kHz时，传递函数的幅值远小于1，即贯通式同相AT牵引供电系统的边界元件对故障信号的高频分量有较强的衰减作用。

1.2 牵引网单端电流方向保护原理

牵引网线路及边界对故障电流高频分量的衰减作用不同。当牵引网的距离较短时，边界对高频分量的衰减作用将大于牵引网对高频分量的衰减作用。当牵引网的长度超过某个临界值时，牵引网对故障电流高频分量的衰减作用可能会大于边界对故障电流高频分量的衰减作用，这样会导致牵引网区内故障时保护安装处检测到的高频分量小于本侧区外故障时保护安装处检测到的高频分量，引发保护拒动[12]。

保护安装处区内故障和本侧区外故障时，可以根据保护安装处检测到的故障电流波形突变点极性判定是否为本侧区外发生故障[6]。利用归一化后形态谱值的大小来表示保护装置检测到的故障电流线模信号中高频分量的大小，通过比较阈值与形态谱值的大小来判定区内故障或对侧区外故障。由上述原理提出基于形态学的贯通式同相AT牵引供电系统牵引网单端电流方向保护方法，结合图5进行说明，步骤如下：

(1)提取保护安装处检测到的故障暂态电流进行相模变换。因线模信号中含有的故障高频分量比零模信号多，故选取线模信号作为研究对象。通过MMG变换分析故障电流线模分量波形突变点的极性来判断是本侧区外故障(极性为负，故障f1)，还是区内故障或对侧区外故障(极性为正，区内故障f2、f3、f4或对侧区外故障f5)。

(2)若方向元件判断出故障不是本侧区外故障(即故障不是发生在f1处)，则需进行形态谱运算得到其形态谱，为消除不同尺度的影响，需要将得到的形态谱归一化后变换到频域。再分别对不同尺度下的形态谱求和，得到不同尺度下的形态谱值，并将得到的形态谱值进行归一化。

(3)最终通过比较归一化后的形态谱值Q1与阈值Q的大小来判定区内故障或对侧区外故障。当故障电流线模分量的形态谱值Q1大于阈值Q(Q=1)时，为区内故障(故障f2、f3、f4)；当故障电流线模分量的形态谱值Q1小于阈值Q且大于零时，为对侧区外故障(故障f5)。

贯通式同相AT牵引供电系统牵引网单端电流方向暂态保护的布置如图5所示，保护检测点在牵引变电所2的区内出口处。规定牵引变电所1、2之间的牵引网为保护区内，本侧区外为牵引变电所2的左侧，对侧区外为牵引变电所1的右侧。

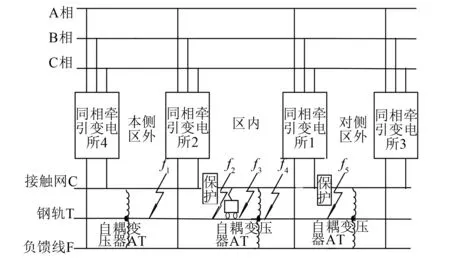
图5 牵引网单端电流方向暂态保护布置图

2 电流方向起动元件

2.1 构造方向起动元件

设定母线流向线路为电流正方向。在图5中，当故障发生在本侧区外f1处，电流方向与正方向相同，电流的突变方向为反方向即在波形突变处极性为负；当区内f2、f3、f4处或者对侧区外f5处发生故障时，电流方向与正方向相反，电流突变方向为正方向即在波形突变处极性为正[13]。由此可知，可以通过判定保护装置处检测到的故障电流波形突变点的极性构造方向起动元件。若故障电流波形突变处极性为负，则本侧区外发生故障，保护应可靠不动作；若故障电流波形突变处极性为正，则是区内故障或对侧区外故障，需进一步判断故障位置。

2.2 基于MMG技术的电流极性判断

本文采用MMG技术对保护安装处检测到的故障电流线模分量进行信号处理，可以通过提取电流信号的上升沿、下降沿来分析电流信号的极性[14-15]。

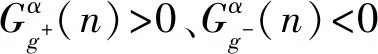
(12)

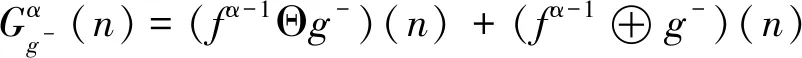
(13)

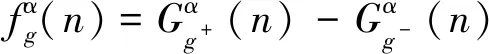
(14)

(15)

设置采样频率为40 kHz，采样点个数为200，选取MMG变换系数α为2的一层进行分析，得到故障电流线模分量的波形如图6所示。

图6 经MMG变换后的故障电流线模分量波形图

从图6中可以明显看出第1层(本侧区外故障)故障电流线模分量波形突变点处极性为负；第2层(区内故障)和第3层(对侧区外故障)故障电流线模分量波形突变点处极性为正。因此通过分析故障电流线模分量波形突变点处的极性可以构造方向起动元件。

3 区内故障与对侧区外故障的判据

当贯通式同相AT牵引供电系统牵引网发生故障后，若方向起动元件判断出不是本侧区外故障，则需进行形态谱运算并比较形态谱值与阈值的大小，进而判定区内故障或对侧区外故障。

3.1 形态谱原理

牵引网区内故障或对侧区外故障时，本文采用形态谱值的大小来表示保护装置检测到的高频分量的大小。当故障发生在对侧区外时，故障电流线模分量要经过牵引网及边界的共同衰减作用才能到达保护安装处，区内故障时电流线模分量仅经过牵引网的衰减作用便到达保护安装处，故区内故障时线模电流高频分量必然大于对侧区外故障时线模电流高频分量。设原始信号为f(x)，则其形态学的开运算、闭运算为[6]

(f°rg)=(fΘrg)⊕rg,r>0

(16)

(f·rg)=(f⊕rg)Θrg,r>0

(17)

式中：°表示开运算;·表示闭运算;r为结构元素的半径;g(x)为一凸结构函数。设定义域Rm内的面积为A，则形态谱表达式如下:

(18)

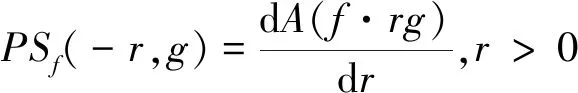
(19)

形态谱结构元素类型丰富，本文选取扁平形结构元素，因为不需考虑结构元素的高度且随着宽度的变化而变化，通过频率的不断改变对信号进行逐频率分解[16]。

结构元素宽度的选取需要注意：结构元素的宽度必须大于故障信号的干扰宽度，否则不能有效过滤噪声，但宽度选择过大会干扰波形的局部及细节特征。当结构元素形状和结构元素宽度选定时，信号采样点数对形态学的频率响应特性并无影响，只会改变频率分辨率[17-18]。对贯通式同相AT牵引供电系统牵引网的区内和对侧区外进行故障仿真，故障电流通过形态谱运算后其线模分量形态谱如图7、图8所示。

图7 区内故障时电流线模分量的形态谱

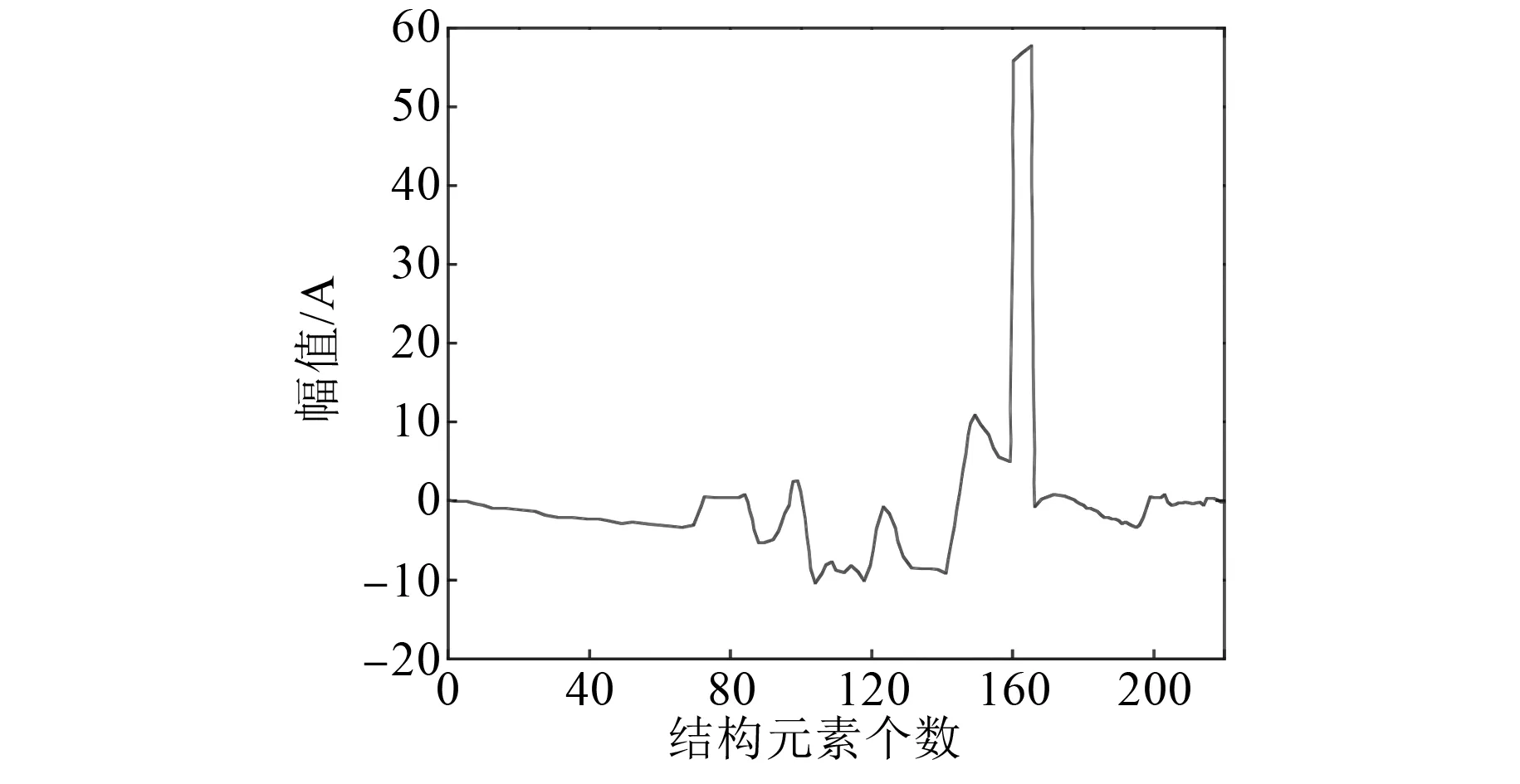
图8 对侧区外故障时电流线模分量的形态谱

由图7和图8可知，当结构元素的宽度接近180时，无论故障发生在区内还是对侧区外，故障电流线模分量波形的形态谱值均接近0。结构元素的个数大于180时，区内故障及对侧区外故障的谱线值均为0，将会对波形的局部特征及细节特征造成影响，故本文选取结构元素的宽度为1～180。不同的谱尺度对应不同的小波分解层数及不同的频段，对应关系如表1所示。

表1 频域内多尺度小波分解层数与形态谱尺度之间的对应关系

3.2 区内故障和对侧区外故障的判别

通过形态谱运算得到形态谱，并对其进行归一化处理，消除尺度变换对形态谱的影响；对不同尺度下的形态谱分别求和，得到不同尺度下的形态谱值并进行归一化，最终得到归一化处理后的形态谱值Qi(i=1、2、3、4、5)。由于形态谱尺度128～256对应的频段很低，不宜用于牵引网单端电流方向暂态保护，故将其舍弃。因此Q1、Q2、Q3、Q4、Q5对应的尺度分别为1～8、8～16、16～32、32～64、64～128。

通过大量仿真结果可知，高频段的形态谱值Q1在区内故障时分布在100～101，故障发生在对侧区外时，经过牵引网及边界共同的衰减作用后形态谱的谱值Q1均分布在10-1数量级，比区内故障时大约降低一个数量级。低频段形态谱值Q2、Q3、Q4、Q5，在区内故障时较均匀地分布在10-1数量级附近，对侧区外故障与区内故障时的形态谱值相比，变化并不大，这是由于牵引网边界自身通低频阻高频的特性造成的，边界对低频分量的衰减作用并不明显，而对高频分量有较强的衰减作用。因此，本文选取了对区内故障、对侧区外故障反应较灵敏的高频段形态谱值Q1作为研究对象，且将Q1放大了102倍以方便后续工作的开展。设定阈值Q为1，将最终得到的归一化后的高频段形态谱值Q1与阈值Q进行比较，从而构成故障判据：当Q1大于Q时，故障发生在区内；当Q1小于Q且大于0时，故障发生在对侧区外。

4 仿真验证

本文参照图1，利用PSCAD平台搭建贯通式同相AT牵引供电系统仿真模型，模型参数如下：电压取220 kV/27.5 kV；频率为50 Hz；通过三相PWM整流与单相PWM逆变的变换方式来构成三相-单相变换，并利用SPWM调制技术输出以基波为主的单相交流电，同时抑制高次谐波的产生[19]；电力机车模型选取总牵引功率为4 800 kW的CHR2型交-直-交电动机车。

本文针对不同的故障初始角、故障位置及不同的过渡电阻等多种情况进行大量故障仿真。采样频率设置为40 kHz，扁平结构元素的宽度为1～180，根据滤波窗宽度(=结构元素宽度/采样频率)的计算公式可得滤波窗为4.5 ms。故障初始角为10°时，不同故障位置及不同过渡电阻条件下的仿真结果如表2所示。

分析表2可知，在故障初始角一定的情况下改变故障位置及过渡电阻：本侧区外故障时，故障电流线模分量波形突变点的极性为负；区内故障时，故障电流线模分量波形突变点的极性为正，且故障电流线模分量的形态谱值Q1均大于阈值Q(Q=1)；当对侧区外发生故障时，故障电流线模分量波形突变点的极性为正，且故障电流线模分量的形态谱值Q1均小于阈值Q并大于0。通过仿真结果还可以看出，故障位置距离保护检测点越远，形态谱值越小；随着过渡电阻的增大，形态谱值减小。

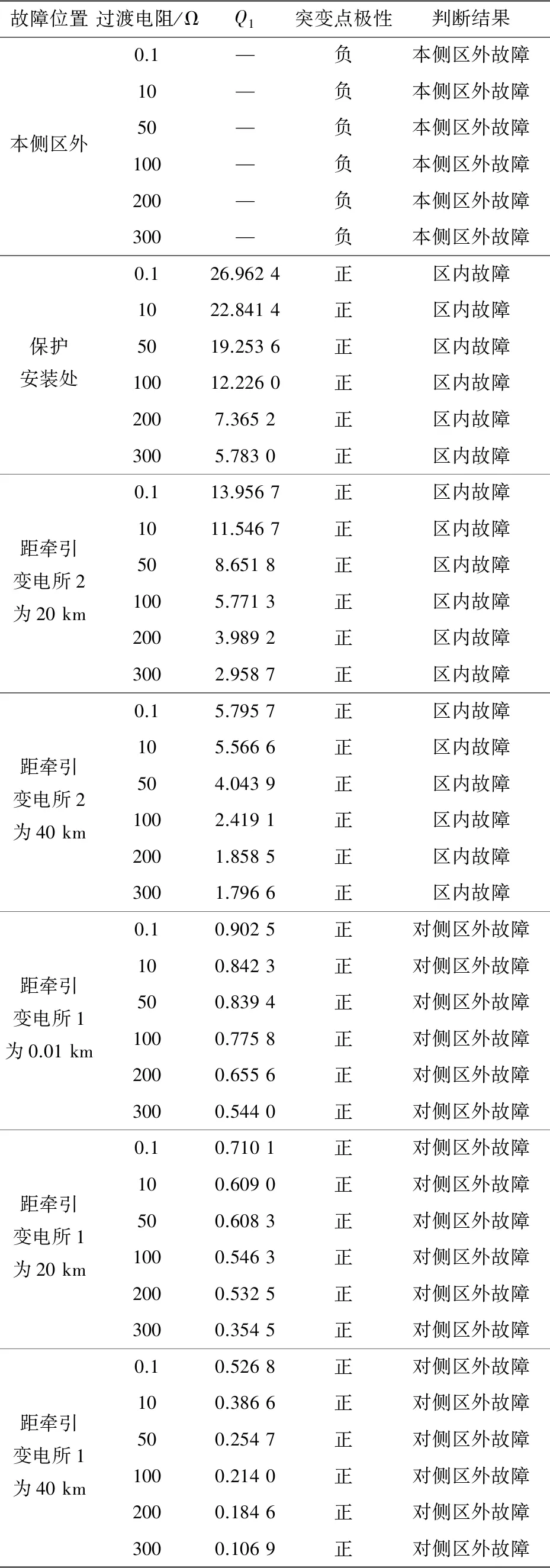
表2 故障初始角为10°时的仿真结果

过渡电阻设置为0.1 Ω时，不同故障初始角及不同故障位置条件下的仿真结果如表3所示。

通过分析表3可知，在过渡电阻一定的情况下改变故障位置及故障初始角：故障发生在本侧区外时，故障电流线模分量的波形突变点极性为负；区内故障及对侧区外故障时故障电流线模分量的波形突变点极性为正；发生区内故障时，故障电流线模分量的形态谱值Q1均大于阈值Q(Q=1)；当发生对侧区外故障时，故障电流线模分量的形态谱值Q1均小于阈值Q且大于0。且故障位置越接近保护安装处、故障初始角越大，则形态谱值越大。

表3 过渡电阻为0.1 Ω时的仿真结果

5 结 语

基于牵引网边界对高频分量有较强的衰减作用，提出一种基于形态学的贯通式同相AT牵引供电系统牵引网单端电流方向暂态保护方法，通过大量故障仿真验证了所提保护方法的可行性，主要结论如下：

(1)通过对故障电流线模分量进行MMG变换，可以得到故障电流线模分量波形突变点的极性：若极性为负，判定为本侧区外故障；若极性为正，判定为区内故障或对侧区外故障。

(2)当判定为区内故障或对侧区外故障时，通过形态谱运算对故障电流线模分量进行处理，并变换归一化后的形态谱到频域。通过比较频域下的形态谱值Q1与阈值Q的大小，判断故障发生位置：当形态谱值Q1大于阈值Q时，为区内故障；当形态谱值Q1小于阈值Q且大于0时，为对侧区外故障。