基于应变模态的风机塔筒法兰螺栓断裂损伤监测研究*
2021-10-27张则荣李鹏飞韩桐桐樊智敏
张则荣,李鹏飞,韩桐桐,樊智敏
(青岛科技大学 机电工程学院,山东 青岛 266061)
0 引 言
风能是重要的可再生能源[1-2]。近年来,风力发电机单机容量逐渐扩大,叶片更长、塔筒更高,使得风机承受的动态负载更大,导致风机在寿命周期内存在较高的故障率[3-5]。风机塔筒的安全性能主要取决于高强度螺栓的连接可靠性,如果螺栓连接在高强度的动态载荷下断裂失效,且断裂数目增多,就会导致风机塔筒的折断使风机发生倒塌事故[6-8]。因此,对风机塔筒法兰处螺栓断裂进行损伤识别监测意义重大。
结构的模态参数对结构的局部损伤非常敏感,局部损伤的出现会使模态参数发生改变。因此,采用振动模态分析技术对结构进行无损检测是一种经济高效的监测方法。陆秋海等人[9]验证了应变类指标比位移类指标对损伤更敏感,应变类指标对结构损伤具有更高的识别能力。WANG T等人[10]采用工作模态分析和应变模态分析法,对四跨桥梁模型进行了识别和损伤定位。张则荣等人[11]基于模态理论对振动筛横梁进行了裂纹损伤识别,表明应变模态对横梁损伤更敏感。CUI Hong-yu等人[12]提出了基于应变模态的自然激励技术,结合特征系统实现算法来识别结构在环境激励下的应变模态参数。
目前,针对基于应变模态进行损伤识别的研究主要集中在土木工程的梁、板等框架结构,用于大尺寸、高耸的风机塔筒的损伤研究还比较少,且根据应变模态来确定螺栓断裂损伤研究亦鲜有报道。
本文通过建立塔筒有限元模型,在塔筒法兰螺栓连接处模拟不同螺栓数目和位置的断裂损伤情况,采用应变模态理论对损伤进行识别诊断,之后优化传感器布置,建立修正的应变绝对偏差损伤识别指标,以提高损伤识别的敏感度。
1 基于连续梁的应变模态理论
本文将风电塔筒假设为梁结构,运用连续体振动微分方程法,建立应变模态。假设梁为伯努利-欧拉梁,在xoy平面内做横向微振,发生弯曲变形。
由达朗贝尔原理构建连续梁的自由振动微分方程为:
(1)
式中:E—梁的弹性模量;I—截面对中性轴的惯性矩;ρ—单位体积梁的密度;S—梁横截面面积;y(x,t)—距原点x处的截面在t时刻的横向位移,即挠度。
运用模态叠加概念,将式(1)中的挠度y(x,t)设为:
(2)
梁在任意截面的弯曲振动曲率变化函数表示为:
(3)
式中:φr(x)—满足梁两端几何边界条件的模态振型;qr(t)—对应的第r阶的模态坐标;ρ(x,t)—振动梁的曲率半径。
由挠曲线近似微分方程得弯矩与挠度的关系为:
(4)
由式(3,4)可得:
(5)
工程实际中,对曲率响应的测量非常困难,因此可以根据实验模态分析方法先识别位移模态振型,再进行二阶中心差分,从而得到结构的离散应变模态振型和离散曲率模态振型的近似解。
笔者将n截面处以差分方程的形式表示式(3),并代入式(5),则对于沿着连续梁的3个等距测点有:
(6)
式中:fn—n截面处梁的弯曲挠度;fn+1,fn-1—相邻的沿梁与n截面相距Δ的两测点处梁的弯曲挠度。
梁的弯曲变形和应变ε相对应,代入式(3)则应变可表示为:
(7)
式中:h—梁中性面到应变点的距离。
由上式可知,连续梁结构的应变模态是位移模态的二阶导数。由于位移到应变是微分过程,位移中存在的微小变化将在求导后的应变中得到放大,从而得到应变参数的显著变化。
因此,应变类参数对结构的微小损失比较敏感,这为结构发生微小损伤后使用应变类参数进行损伤识别提供了理论依据[13]。
2 风电塔筒的位移和应变模态分析
本文以某1.5 MW风机为研究对象,其塔筒总高70.65 m(共分为3段,下塔筒高21 m,中塔筒高23.75 m,上塔筒高25.9 m)。风机塔筒底部直径4 m,顶部直径2.6 m,壁厚由底部30 mm向顶部18 mm过渡,塔筒段间通过法兰螺栓连接。在塔筒顶部建立4 m×4 m×4 m的质量块,设置其密度为1 250 kg/m3,以此来等效代替叶片和机舱;质量块的重心与塔筒的轴线有0.2 m的偏心距,模拟实际叶片和机舱对塔筒的弯矩。
笔者在SolidWorks中进行1∶1建模装配,并导入ANSYS Workbench中,设置弹性模量E=213 GPa,密度ρ=7.8×103 kg/m3,泊松比μ=0.28。
塔筒有限元模型如图1所示。

图1 塔筒有限元模型
图1中,约束固定第1法兰段的底面。塔筒中各体的接触类型设置为:螺栓与螺母绑定接触;螺母与垫片绑定接触;螺栓、螺母与法兰端面之间为绑定接触;塔筒段法兰端面之间为有摩擦接触,摩擦系数为0.2;顶部质量块与上塔筒的上法兰端面为绑定接触。
塔筒模型的单元类型为实体单元,设置网格大小为0.5 m,进行四面体自由网格划分,在塔筒段法兰接触处细化网格。划分总节点数为723 018,总单元数为407 150。法兰螺栓连接处网格划分如图2所示。

图2 法兰螺栓连接处网格划分
笔者对第2法兰段和第3法兰段上的每个螺栓分别施加480 kN和320 kN的预紧力,模拟实际情况下法兰的螺栓连接情况。彭文春等人[14]指出在考虑风载时,在下塔筒和中塔筒的连接处出现最大应力点。因此在第2法兰段螺栓连接处集中设置螺栓断裂损伤,即去除不同数目的螺栓,并根据螺栓断裂的数目设置工况,如表1所示。

表1 螺栓断裂损伤工况设置
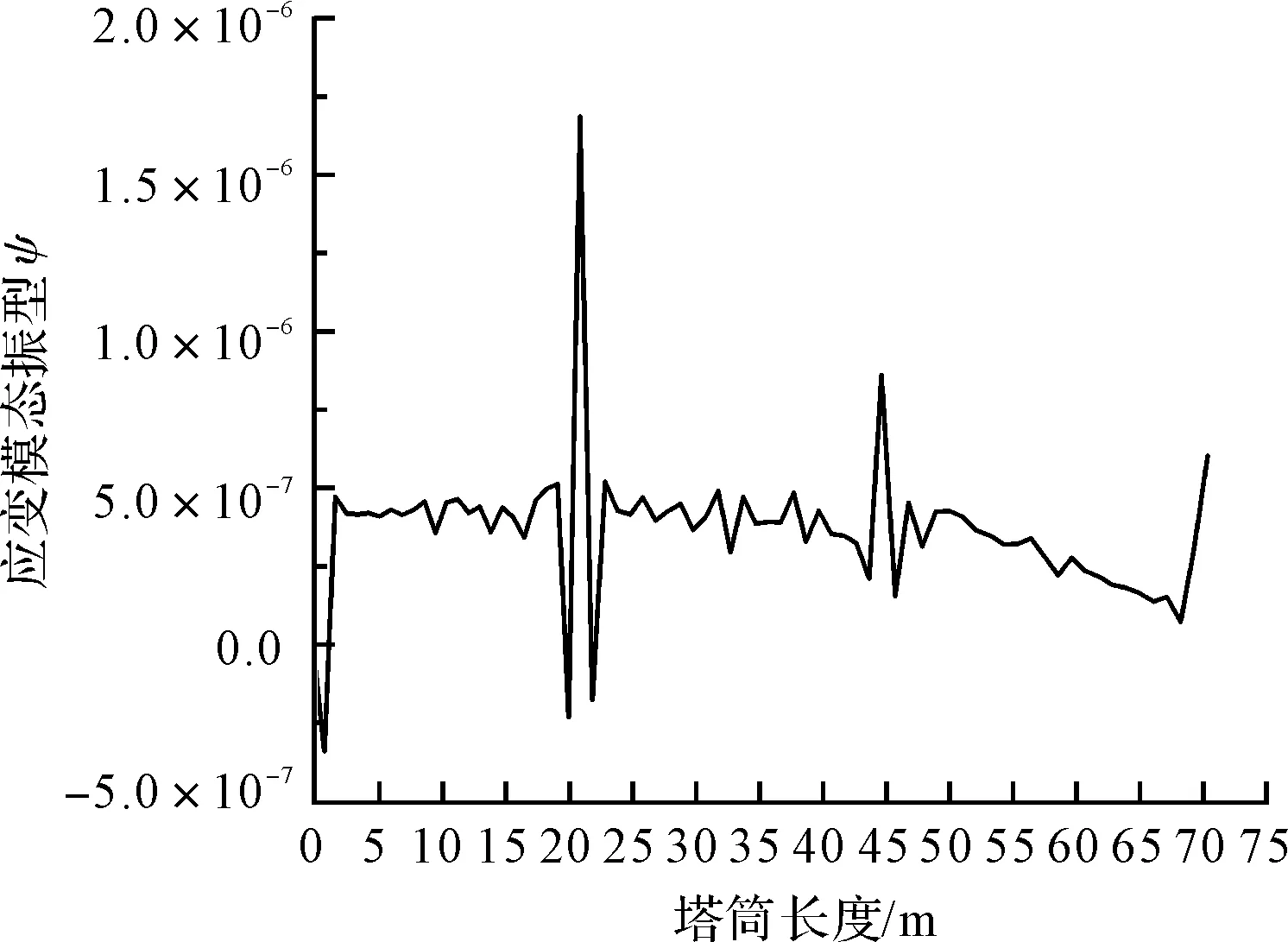
风机塔筒的模态振型为等值线图,不能表达应变模态振型变化的特点,因此沿塔筒的高度方向在筒壁上取一条母线,分析母线上位移和应变模态振型的变化趋势。工况4的一、二、四阶位移模态振型和应变模态振型如图3所示。

(a)一阶位移模态振型
(b)一阶应变模态振型

(c)二阶位移模态振型

(d)二阶应变模态振型

(e)四阶应变模态振型

(f)四阶应变模态振型
由图3可见:位移模态振型在高21 m的第2法兰段处没有因螺栓的断裂而产生突变,而应变模态振型在螺栓断裂的损伤处产生了突变;在44.75 m处,即第3法兰段连接处应变模态振型也发生了微小突变,经分析发现是由于在建模装配时,三维软件圆分辨率的限制导致法兰圈的圆拟合度不够而使接触处有微小凸起,而当母线经过这里时就会有微小突变;同理,该误差在第2法兰段21 m处也会存在一定干扰。
不同工况下的一阶应变模态振型对比,如图4所示。

图4 不同工况下的一阶应变模态振型
由图4可知:应变模态振型在塔筒螺栓断裂位置出现了突变峰值,而且螺栓断裂数目越多突变的峰值就越高;在第3法兰段无损伤处因建模软件的误差而有微小突变,但5种工况在此处的突变几乎重合,所以不会干扰损伤识别;不同工况下应变模态振型有微小偏移,该偏移会对后期损伤程度的判定产生影响。因此直接通过应变模态振型识别螺栓损伤误差较大,损伤指标需修正。
3 风机塔筒损伤监测
以上数值模拟验证了应变模态在风机塔筒法兰螺栓断裂损伤初步诊断的良好效果,但也存在两个问题:(1)在实际工程中,因成本以及风机所处的恶劣环境,不可能在塔筒母线上布置较多的传感器;(2)损伤工况下应变模态振型与无损工况下的应变模态振型存在偏移,该偏移会对后期损伤程度的判断造成干扰。
因此,本节提出新的传感器布置方式,验证应变模态损伤识别的效果,并对损伤识别后应变模态振型的偏移问题进行修正。
3.1 传感器布置优化与工况设置
笔者初步考虑在靠近第2法兰段的下塔筒和靠近第3法兰段的中塔筒的圆周方向模拟布置传感器,每个圆周等分12个点,即每隔30°设置一个应变片,共24个,以验证其单处损伤和多处损伤的识别效果。
在塔筒剖去质量块和部分上塔筒后的俯视图中,传感器拟布置位置如图5所示。

图5 传感器布置位置
接下来,通过数值模拟验证不同工况下的损伤识别效果。设4种工况:单法兰单损伤(工况6)、双法兰单损伤(工况7)、单法兰双损伤(工况8)和双法兰双损伤(工况9)。
优化后传感器的工况设置如表2所示。

表2 优化后传感器的工况设置
3.2 应变绝对偏差损伤识别指标的建立
损伤识别指标定义为应变绝对偏差,即:
(8)

为统一基本量度单位,以及方便对测量数据进行观察,笔者对数据进行归一化处理,得到各工况下不同测点的应变绝对偏差归一化值,如图(6~9)所示。
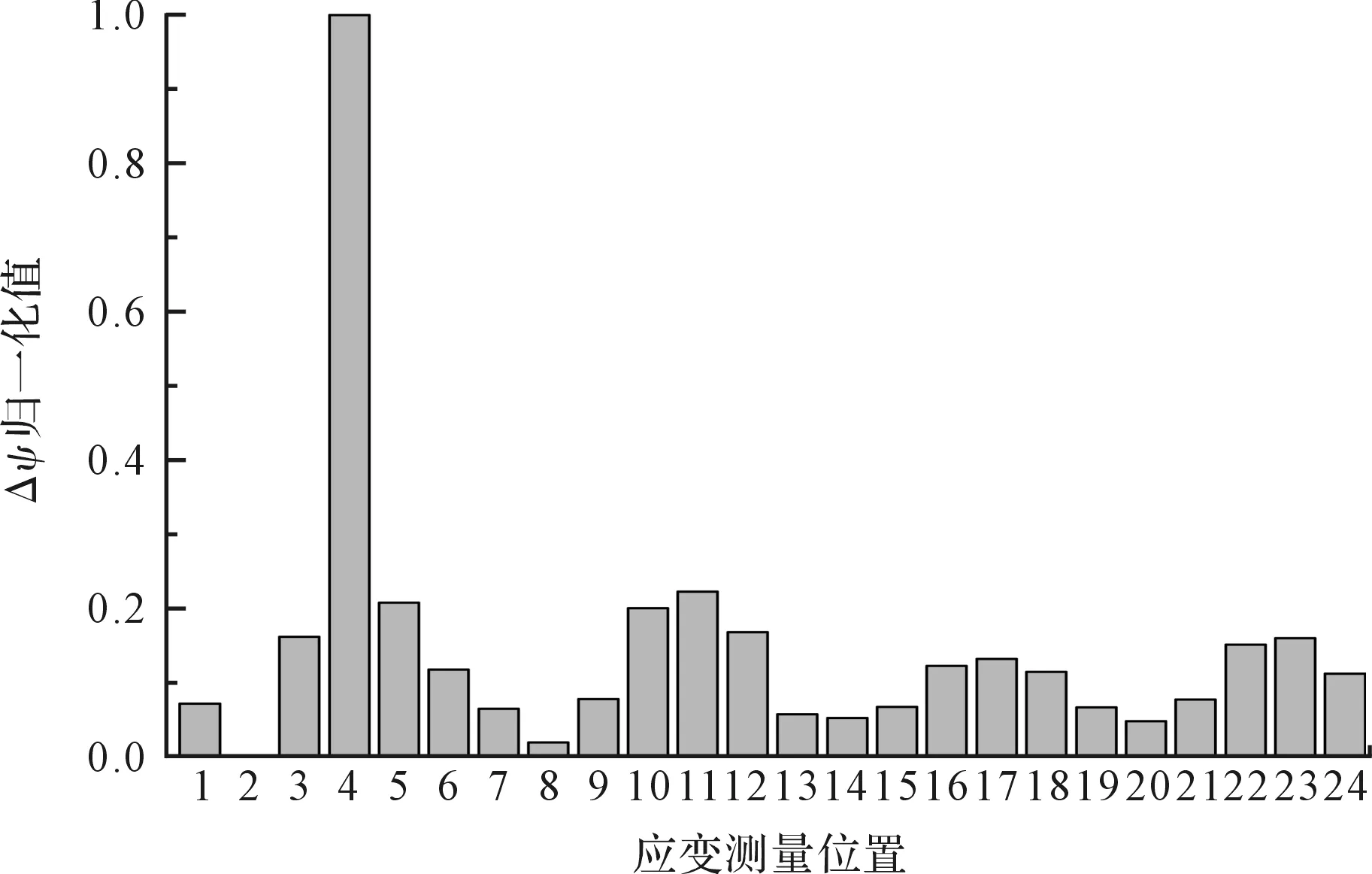
图6 工况6各测点ΔΨ归一化值

图7 工况7各测点ΔΨ归一化值

图8 工况8各测点ΔΨ归一化值

图9 工况9各测点ΔΨ归一化值
经观察发现:由于塔筒为对称结构在一阶弯曲模态下,24个应变测点的应变值具有规律的波动性。在第2法兰段的1~12应变测点中,损伤测点4和10对损伤敏感,损伤处的ΔΨ归一化值突出显著,而且断裂的螺栓数目越多,值越大;
在第3法兰段的13~24应变测点中,对比图(6~9)可发现:在损伤测点17和20处的ΔΨ归一化值略有增大,其螺栓断裂数目越多,应变值越大;但由于应变模态振型偏移的存在,未损伤处的应变值使得第3法兰段损伤处应变值突出不明显,对损伤识别产生了一定的干扰。
3.3 应变绝对偏差损伤识别指标的修正
基于上述存在应变模态振型偏移干扰和第3法兰段损伤识别不敏感的问题,笔者建立新的损伤识别指标进行修正。
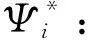
(9)
修正后新的损伤识别指标为:
(10)

最后得到修正后工况(6~9)的损伤识别情况,如图(10~13)所示。

图10 工况6各测点Ψ′归一化值

图11 工况7各测点Ψ′归一化值

图12 工况8各测点Ψ′归一化值

图13 工况9各测点Ψ′归一化值
为了验证修正前、后损伤识别指标的敏感度,笔者进一步分析了传感器优化布置后在各损伤位置的损伤识别率情况,分别定义损伤识别指标修正前、后的损伤识别率为ηa、ηb:
(11)
(12)
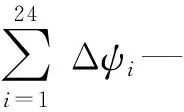
识别指标修正前、后的损伤识别率如表3所示。

表3 损伤识别指标修正前、后各工况下的损伤识别率
由图(10~13)及表3可知:修正后损伤识别指标的损伤识别率更高,对损伤位置更加敏感;同时,无损伤测点的干扰度降低,第3法兰段对损伤不敏感的情况也有了改善。
因此,针对不同法兰段、不同位置、不同螺栓断裂数目的损伤情况,在传感器位置优化的基础上,采用修正损伤识别指标有更好的损伤诊断能力。
4 结束语
本研究采用应变模态理论对风机塔筒法兰处螺栓断裂损伤进行无损检测,通过仿真分析,研究不同损伤工况下的位移和应变模态振型变化,并初步优化传感器布置,建立了高敏感度的修正应变绝对偏差损伤识别指标。研究结果表明:
(1)风机塔筒法兰螺栓不同断裂数目下,位移模态振型无明显变化,而应变模态振型在损伤的局部位置出现了突变峰值,证明应变模态比位移模态对损伤更加敏感;
(2)基于修正的应变绝对偏差损伤识别指标,解决了风机塔筒应变振型发生偏移影响损伤识别的问题,进一步提高了应变模态对风机塔筒法兰螺栓断裂损伤识别的敏感度。
在后续的研究中,笔者将构建叶片、轮毂、机舱、塔筒和基础的完整有限元模型,以提高仿真分析的真实性;同时,进行实验以验证并对比仿真结果,优化仿真分析过程,提高理论仿真分析的准确性。
