1 600 m 双塔自锚式斜拉桥结构整体稳定性分析
2021-10-27姜洋
姜洋
[上海市政工程设计研究总院(集团)有限公司,上海市 200092]
0 引言
斜拉桥是由塔、梁、索和基础共同受力的结构体系,因其跨越能力强、受力明确合理、力学性能好、造型优美等优点,在过去半个多世纪里取得了快速的发展。近年来,斜拉桥的主跨跨径记录不断刷新,我国在建的常泰长江大桥主跨已达1 176 m。随着斜拉桥主跨跨径的增加,主梁的高跨比越来越小,桥塔高度越来越高,桥梁整体稳定性问题已成为其主跨跨径进一步增加的限制因素[1-4]。
对于主跨1 600 m 的自锚式斜拉桥,桥塔处主梁承受巨大的轴向压力,主梁的整体稳定性成为控制结构受力的关键因素。现以某公路通道方案为工程背景,对影响超大跨径自锚式斜拉桥结构整体稳定性的一些主要因素开展参数研究。
1 总体布置方案
某公路通道位于河口变迁河段,河槽冲刷深度达40m 以上,由于河槽不稳定,通航宽度不仅需要考虑深槽宽度,还必须为河槽的变迁预留足够的空间。依据现有水文、通航资料和可选桥址进行研判,桥位处主桥跨径需求为单主跨1 600 m。
主桥设计方案的桥型结构为双塔自锚式斜拉桥,桥跨布置为3×110+390+1 600+390+ 3×110=3040(m),边中跨比0.45。桥塔处主梁为竖向支撑体系,横向设置抗风支座,桥塔处设置塔梁间纵桥向弹性索,采用沉井基础,总体布置如图1 所示。

图1 主跨1 600 m 双塔自锚式斜拉桥总体布置图(单位:m)
桥塔高度为430 m,其中桥面以上桥塔高度为350 m,下塔柱高度为80 m。桥塔纵桥向为独柱型,塔顶纵桥向尺寸为12 m,塔底为25 m;横桥向为钻石型,塔顶横桥向尺寸为12 m,塔底为15 m,见图2 所示。

图2 桥塔布置图(单位:m)
主梁采用分离式(中央开槽)扁平钢箱梁断面形式,全宽52 m,高度5.5 m。顶板板厚16 mm,底板板厚28~60 mm,腹板板厚20~50 mm,见图3 所示。

图3 主梁标准断图(单位:cm)
斜拉索为双索面扇形布置,梁上拉索锚点位于主梁两侧,塔中心处标准索距为2.5 m,梁上标准索距为20 m,边跨梁端索距减小到16 m 和12 m。斜拉索采用平行钢丝拉索,最大拉索规格φ7-547。
2 结构整体稳定性参数分析
经试算,结构可能出现两种失稳模态,分别为主跨和边跨主梁失稳,失稳模态分别见图4 和图5 所示。

图4 主跨主梁失稳图示

图5 边跨主梁失稳图示
接着,对影响斜拉桥结构整体稳定性的五个主要因素,即主梁梁高、辅助墩数量、塔梁约束、桥塔高度和塔上锚固间距进行参数分析,以确定各参数的合理取值。
2.1 主梁梁高
边跨设置三个辅助墩,塔梁间纵桥向弹性索刚度为100 MN/m,主梁梁高分别取5.0 m、5.5 m 和6.0 m时,结构的一阶弹性稳定系数见表1 所列。
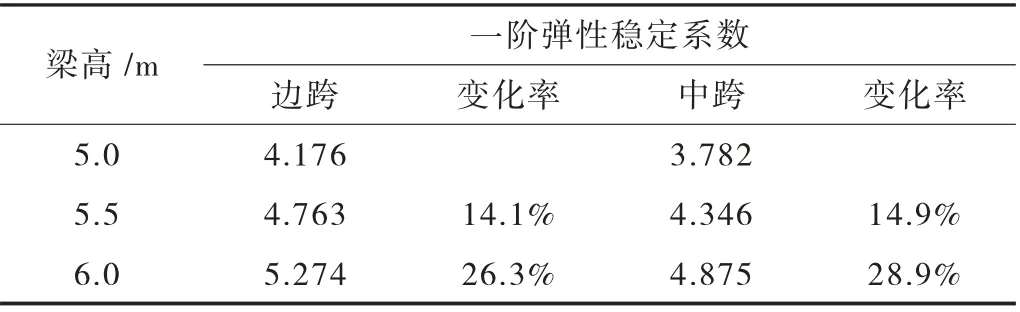
表1 梁高对一阶弹性稳定系数的影响一览表
从表1 可以得出以下主要结论:
(1)在边跨设置三个辅助墩时,失稳模态均为中跨主梁失稳;
(2)随着梁高的增加,中、边跨一阶弹性稳定系数均随之增加。
增加梁高有利于提高结构整体稳定性,但梁高增加将导致主梁迎风面积增加,主梁承受的横风荷载增大,使得结构在极限横风作用下的中跨跨中横桥向位移增大,且桥塔的横桥向弯矩也将增加。
因此,在满足结构稳定性的前提下,应选取尽量小的梁高。当梁高为5.5 m 时,结构的一阶弹性稳定系数为4.346,大于4.0,满足规范要求。
2.2 辅助墩数量
塔梁间纵桥向弹性索刚度为100 MN/m,主梁梁高为5.5 m,辅助墩数量分别为1 个、2 个和3 个时,结构的一阶弹性稳定系数见表2 所列。

表2 辅助墩数量对一阶弹性稳定系数的影响一览表
从表2 可以得出以下主要结论:
(1)随着辅助墩数量的增加,中、边跨主梁的一阶弹性稳定系数均增大;
(2) 辅助墩数量对中跨主梁一阶弹性稳定系数的影响很小,对边跨主梁一阶弹性稳定系数的影响相对更大;
(3)当辅助墩数量为1 个和2 个时,边跨主梁先于中跨主梁失稳;当辅助墩数量为3 个时,中跨主梁先于边跨主梁失稳。
因此,辅助墩数量可选取为3 个,可显著提高边跨主梁的稳定性。
2.3 塔梁约束
主梁梁高为5.5 m,边跨设置3 个辅助墩,塔梁间纵桥向弹性索刚度选取为0~400 MN/m 以及纵向固定约束时,结构的一阶弹性稳定系数见表3 所列。
从表3 可以得出以下主要结论:
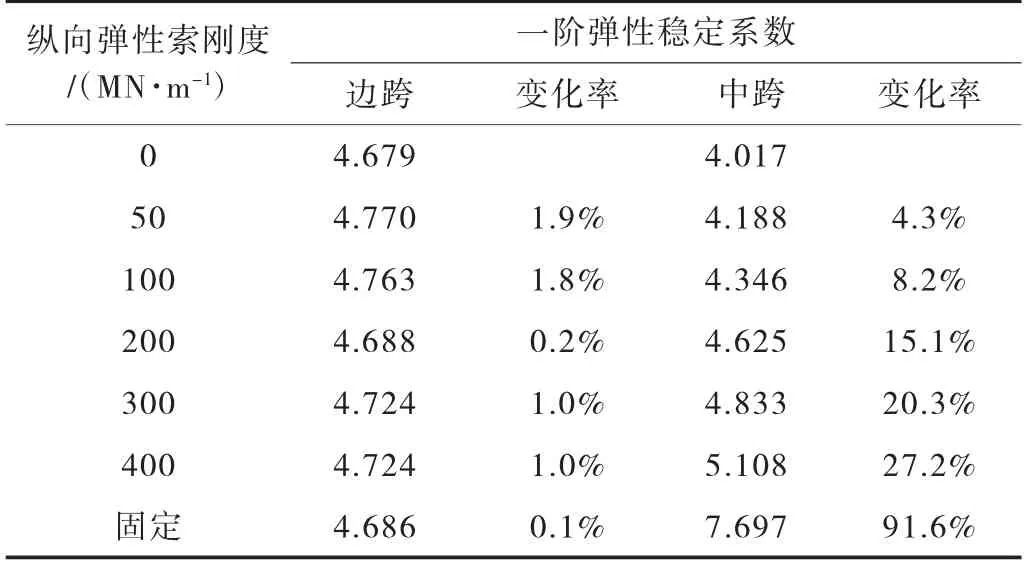
表3 塔梁约束对一阶弹性稳定系数的影响一览表
(1)弹性索纵向刚度对边跨主梁的一阶弹性稳定系数影响很小;
(2)随着弹性索纵向刚度的增加,中跨主梁的一阶弹性稳定系数逐渐增加,但增加的速率越来越小。
随着弹性索纵向刚度的增加,主梁的梁端纵向位移逐渐减小,但塔底的纵向弯矩大幅增加,因此弹性索纵向刚度不宜取值过大。
当弹性索纵向刚度取50 MN/m 时,结构的一阶弹性稳定系数为4.188,大于4.0,满足规范要求。
2.4 桥塔高度
主梁梁高为5.5 m,边跨设置3 个辅助墩,塔梁间纵桥向弹性索刚度为50 MN/m,桥塔高度分别选取为430 m、420 m 和410 m 时,结构的一阶弹性稳定系数见表4 所列。

表4 桥塔高度对一阶弹性稳定系数的影响一览表
从表4 可以得出以下主要结论:
(1)随着桥塔高度的降低,拉索的水平倾角变小,拉索的水平分力增加,使得主梁的一阶弹性稳定系数也随之降低;
(2)桥塔高度对于中跨主梁的一阶弹性稳定系数影响更大。
增加桥塔高度可提高结构的整体稳定性,但也随之增大了桥塔的施工难度,因此在满足结构稳定性的前提下,应选取小的桥塔高度,430 m 的桥塔高度是合适的。
2.5 塔上锚固间距
桥塔高度保持430 m 不变,塔上锚固间距分别为2.2 m、2.5 m 和2.8 m 时,结构的一阶弹性稳定系数见表5 所列。

表5 塔上锚固间距对一阶弹性稳定系数的影响一览表
从表5 可以得出以下主要结论:
(1)桥塔高度不变时,随着塔上锚固间距的增加,拉索的水平倾角变小,拉索的水平分力增加,使得主梁的一阶弹性稳定系数也随之降低;
(2)塔上锚固间距对于中、边跨主梁的一阶弹性稳定系数影响程度接近。
减小塔上锚固间距可提高结构的整体稳定性,因此可根据斜拉索在塔上锚固构造的空间要求确定斜拉索的塔上锚固间距。
3 结语
本文对1 600 m 双塔自锚式斜拉桥结构稳定性进行了参数分析,得到以下主要结论:
(1)在满足结构稳定性的前提下,应选取尽量小的梁高;当梁高为5.5 m 时,结构的一阶弹性稳定系数为4.346,大于4.0,满足规范要求。
(2)当辅助墩数量为1 个和2 个时,边跨主梁先于中跨主梁失稳;当辅助墩数量为3 个时,中跨主梁先于边跨主梁失稳,并可显著提高边跨主梁的稳定性。
(3)为了减小塔底的纵向弯矩,弹性索纵向刚度不宜取值过大;当弹性索纵向刚度取50 MN/m 时,结构的一阶弹性稳定系数为4.188,大于4.0,满足规范要求。
(4)在满足结构稳定性的前提下,应选取小的桥塔高度,430 m 的桥塔高度是合适的。
(5)减小塔上锚固间距可提高结构的整体稳定性,可根据斜拉索在塔上锚固构造的空间要求确定斜拉索的塔上锚固间距。
