一类e-HR神经元模型的网络同步控制

刘 畅， 许云召

(信阳职业技术学院 数学与信息工程学院， 河南 信阳 464000)

神经元是构成神经系统的基本非线性单元，神经系统是由无数个神经元构成，每个神经元之间都是相互独立的，具有丰富的放电行为，神经系统接受、编辑和转递生理信息的功能主要通过神经元的放电活动完成。建立神经元模型是为了运用数学的语言来模拟神经元复杂的放电过程与放电活动，这极大地促进了神经工程、信息科学和非线性动力学行为的发展。神经模型由于受到某些因素的影响，可能会表现出某些复杂的动态行为，例如振荡、发散、混沌、不稳定或其他较差的性能。

神经元信号的传递是由于轴突传导和化学突触过程所致，它们被发现在大脑的神经元网络中。文献[1]探究了具有时变时滞的神经网络同步，通过李雅普诺夫函数导出了自适应同步控制准则，得出了自适应同步条件。GUO Sheng-li等[2]通过考虑星形胶质细胞耦联的生物神经元的自身连接，研究了自身驱动诱导反应在电活动中的作用，以Hodgkin-Huxley在神经元上建立了一个简单的网络，并考虑了Autapse效应，结果表明自适应驱动可以使神经元-星形胶质细胞网络产生不同的电活动模式。Handa等[3]首先将多个神经元模型进行电突触耦合，然后探究这些神经元之间的同步问题。除了研究神经元模型的同步之外，研究神经元模型的分岔行为也是极其重要的，分岔包括Hopf分岔、单参数分岔以及双参数分岔等等。文献[4-5]探究了Hindmarsh-Rose神经元模型的动力学行为。文献[4]推导出了Hopf分岔方向的显示公式以及通过Hopf分岔发生的分岔周期解的稳定性；文献[5]为了讨论平衡点处的稳定性，推导出了计算Hopf分岔稳定性定理的公式。与神经元相关的好多疾病都是由神经元的混沌放电以及神经元的同步问题所引起的，所以研究神经元模型的同步就有极其重要的意义[6-9]。文献[10]基于FHN模型，对FHN神经元模型进行研究，发现该模型在外界刺激的作用下能够实现网络同步。文献[11]利用李雅普诺夫稳定性理论设计了自适应反馈同步控制器，研究了新的复杂网络模型的完全同步问题。

本文基于磁通神经元模型，研究磁通神经元模型的神经网络同步，通过构造合适的李雅普诺夫指数，推导出新的自适应反馈同步准则，以此验证所提出的同步准则的有效性。

1 模型描述

磁通e-HR神经元的集体行为能够连接成网络形式，其神经网络模型的微分方程为

(1)

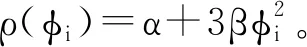
2 网络的自适应反馈同步控制

2.1 同步分析

通常情况一个网络是由N个动力学节点构成的，网络的每个节点是n维非自治动力系统，其网络模型为

(2)

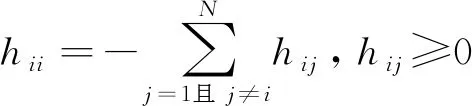
施加控制之后的网络模型为

(3)

式中Ui是使网络达到同步时的控制器。

假设1 对于网络中的微分方程

(4)

其中X∈Rn，f：Rn×Rn→Rn为连续函数，对于任意的初值(t0，X0)都存在唯一解，X0为n维向量。

假设2 对于向量函数f(X(t))，假定Lipschitz条件成立，即对任意的Xi(t)=(xi1(t)，xi2(t)，…，xin(t))T和S(t)=(s1(t)，s2(t)，…，sn(t))T，存在一个正常数L>0，就会有下式成立：

‖f(Xi(t))-f(S(t))‖≤L(‖Xi(t)‖-‖S(t)‖)，

(5)

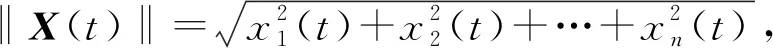
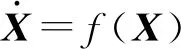
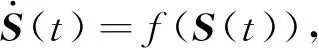
(6)

其中S(t)有可能是相空间的一个平衡点、一个周期轨道或者一个混沌轨道。

注意：对于受控网络模型(3)，外部耦合矩阵H没有必要是对称的，并且hij也没必要必须仅仅是0或1。选取hij=0.1(i≠j)，对于内耦合矩阵A没有什么特别的约束，假设内耦合矩阵A=I5和L=46，则假设1和假设2成立。

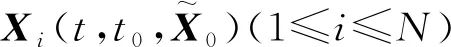
(7)

其中X0∈Ω，1≤i≤N，则称控制网络(3)为渐进网络同步，并且称Γ×Γ×…×Γ为动力学网络(4)的同步区域。

定义误差向量为

Ei(t)=Xi(t)-S(t)=(e1,e2,…,eN)T， 1≤i≤N，

(8)

则误差系统为

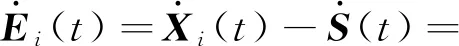
(9)

定义2 若存在M>0，σ>0，使得

‖Ei(t)‖≤Me-σt，

(10)

其中i=1，2，…，N，则称误差系统(8)是渐进稳定的，即受控网络模型(3)是同步的。

下一步需要做的就是要选择一个合适的控制器Ui和一个相应的自适应控制率，使其网络控制系统达到指数渐进同步。

定理1 假定假设1、假设2成立，设控制系统Ui=-diEi(i=1，2，…，N)，并且

(11)

其中μ、δi为正常数(本文取μ=0.2)，那么控制网络(3)达到全局指数渐进同步，且有

(12)

证明首先构造一个Lyapunov函数为

(13)

通过使用不等式XTY≤|XTY|≤‖X‖‖Y‖，并且根据(8)和(10)式，对式(13)进行求导可得：

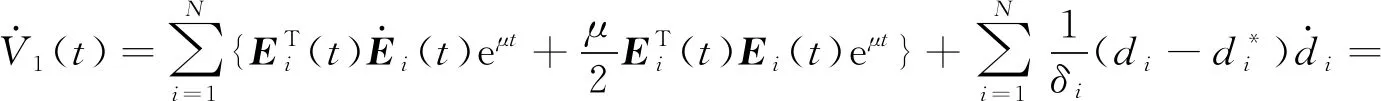
(14)

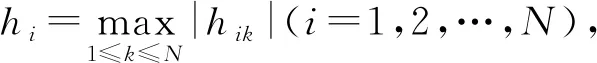
(15)

(16)

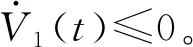
(17)

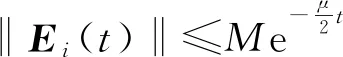
2.2 数值模拟

在数值仿真过程中，取网络的节点数N=50，则可以任意选取神经网络模型(1)中的50个节点的连接方式，其耦合矩阵为

在控制律(12)下相对应的时间响应与同步误差如图1、图2所示。

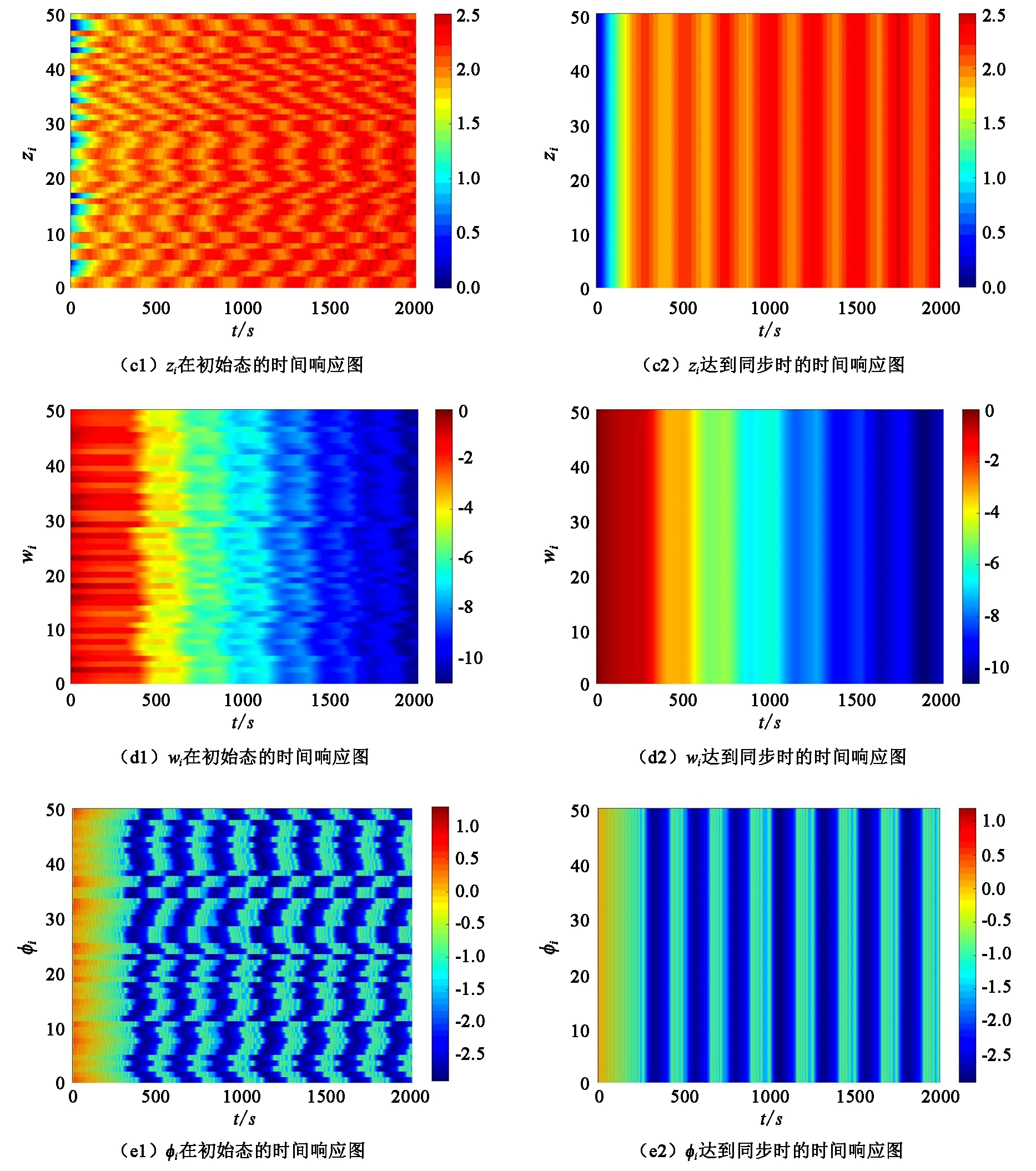
图1 时间响应图

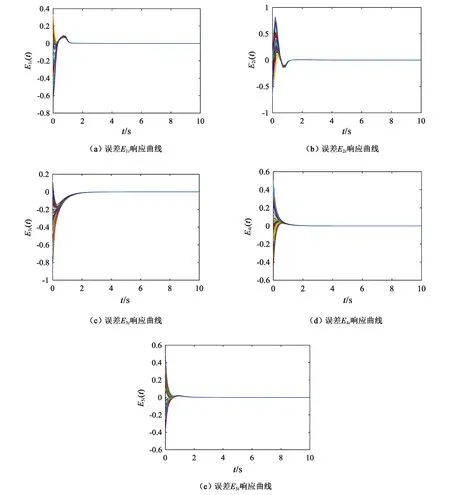
图2 随时间变化的网络同步误差图

从图1中可以很清楚地看出系统在初始状态时保持各自的动力学行为，但在加入控制器之后最终达到了同步；从图2中可以看出在没有加入控制器之前系统的动力学行为是相互的，在加入控制器之后达到了同步。从而说明该控制器的选取是可行性的。另外将文献[13-14]的研究结果与本文的研究结果进行对比，可以发现通过数值模拟能够证明本文所提出的同步是有效的。

3 小结

本文研究的是磁通e-HR神经元模型的网络同步控制，这种网络是一种现实的网络形式，具体来说，通过构造适当的李雅普诺夫函数，推导出了一种新的自适应反馈同步准则。这个准则对于理解复杂网络的同步机制很有用。此外，用于实现网络同步的假设和由此产生的自适应控制器以简单形式表示，可以很容易地应用于实际情况。最后，通过数值模拟验证了所提出的同步准则的有效性。