高考数学关键问题下微专题教学的思考——以“求平面法向量”为例

文/ 广西玉林市教育科学研究所 周志娟

“微专题”是指一个相关联的、可单独研究的知识体系，或者某种数学思想方法、一个研究主题等。数学微专题教学是围绕复习的重难点和考试的热点问题来设计的，立足于具体的学情、教情、考情，选择一些切入点小、角度新、针对性强的“微型”复习专题，利用具有紧密相关性的知识和方法形成的专项研究，力求解决复习中的真问题和实问题。微专题的选取和设计是高三复习教学的关键，源于对考点的细化，对知识的延伸，对易错易混点的辨析，对难点的突破等来进行设计。这就要求教师必须深入了解新课标考情，把握学生学情，有效整合教学资源，才能设计出有效突破高三复习重难点、提高学生解题能力的微专题学案。《立体几何》这一章，学生对内容比较熟悉，方法也比较容易掌握，高考设置的解答题难度中等，学生也比较容易入手，可往往最后的得分不高，通常在应用空间向量法求解问题的关键环节——求平面法向量中出现差错，为此，下面结合“平面法向量的求法及应用”谈谈笔者对微专题教学的一些思考。

一、微专题的内容如何选择和确定

在《立体几何》这一章的复习中，通过对立体几何的核心考点的梳理，可以看到解决问题的关键就是平面法向量的求解。而实际情况中，的确是不少学生对平面向量法向量的求解问题是感到困难的，基于高考的考点要求和学生思维、计算能力的现状，因此在《立体几何》这章设置的微专题就为“求平面法向量”。

二、微专题的目标和重点如何设计

微专题复习课的任务就是抓住重点、突破难点，重点放在帮助学生生成解决问题的基本方法及和数学思想方法，而不只是关注单个题目的具体解法，要防止复习的“碎片化”，避免“就题论题”。在高考复习中，需要有效聚焦在重点和疑点上，在适当的版块增设微专题，以一条明显的逻辑主线串联起相关的知识、题目、方法，帮助学生构建清晰的知识体系，把握一类问题的本质和通法，达到见微知著的效果，提升学生的解题能力。《立体几何》这章设置的微专题《求平面法向量》的目标与重点就是法向量的求法及实际应用训练。

三、微专题如何使学生构建起解决问题的较为清晰的“线路图”

微专题教学的本质就是“为迁移而教”，为培育数学核心素养而教。“为迁移而教”的本质就是塑造学生良好的认知结构。因此，微专题教学就是要重视学生在原有的基础上，从学生思维最近发展区出发设计问题，激活知识梳理，构建起解决某一类问题的较为清晰的“线路图”。传统教学中产生惰性知识的主要原因之一是这些知识没有形成一定的知识网络或图式。遇到实际问题，零散而非结构化保存的知识，不利于提取和使用。因此，微专题复习课要帮助学生梳理本专题所涉及的知识与方法，形成对一类问题更系统、全面的认识。

四、微专题的学习成效如何检验和评估

微专题教学中要引导学生对认知结构中已有的一些解法进行反思与提炼，让学生认识到知识方法之间的联系，帮助学生建立起对一类问题的整体认知，进而生成处理一类问题的基本方法，这样才能让学生举一反三，触类旁通。要重视算理算法，优化解题方法，培养运算能力，教学中需要对学生的解题方法进行梳理、改造，让学生明白每一种方法的优点（适用面）和缺点（不适用面）。在学生已经解答的基础上，可以通过展示学生的解答，点拨方法、纠正错误、规范格式。

下面以“求平面法向量”为例，结合以上四点关于微专题的思考，设计了一节微专题的教学环节。

环节1 知识梳理

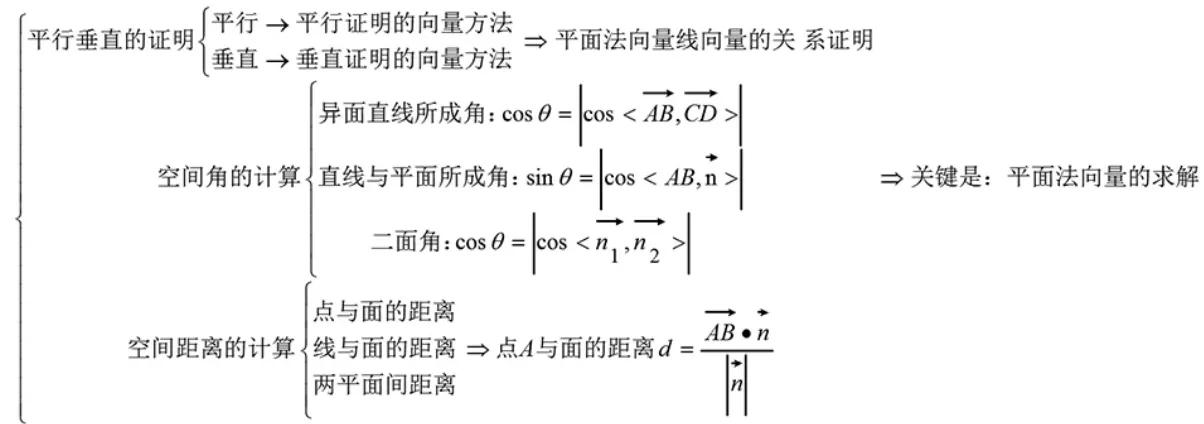
通过对立体几何的核心考点的梳理，可以清晰的看到解决问题的关键就是平面法向量的求解。

环节2 典例讲解

题 1 （2020 年全国高考 III 卷理科第19 题）

如图，在长方体 ABCD -A1B1C1D1中，点E，F 分别在棱DD1，BB1上，且2DE=ED1，BF=2FB1

（1）证明：点 C1 在平面 AEF内；

（2）若 AB=2，AD=1，AA1=3，求二面角A-EF-A1的正弦值。

评析：这是一道经典的高考题，所给几何体是最熟悉的长方体，考察点在平面内的证明，同时也考察了利用空间向量法求解空间向量法，考察推理能力和计算能力，属于中等题。其中在第（2）小问中，关键是分别找出平面AEF 和平面A1EF 的法向量。

微专题教学中，先简单回顾教材中“点乘法”求平面法向量的步骤：设（法向量）→找（平面内两相交向量）→乘（法向量与平面内两相交向量分别做数量积）→赋（对三个未知量中其中一个赋予特殊值）→得（法向量的结果）。方法很清晰，但是计算流程比较繁琐，学生在紧张的考试中容易计算出错，因此再学习另一种求平面法向量的方法——“叉乘法”。

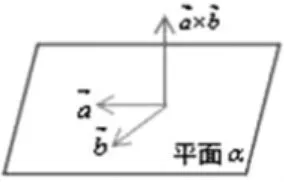
其中“叉乘法”计算法向量的计算口诀可以形象归纳为：求谁盖谁，交叉相乘再相减，注意纵坐标取其相反数。

学习利用“叉乘法”求平面法向量的方法，一方面解决了学生在计算法向量时易错的问题，另一方面对教材知识进行了有效补充，并且不与教材产生知识交叉混淆，完善了学生解决具体问题的方法体系。

环节3 巩固方法形成技能

练习1：图 1 是由矩形 ADEB、RtΔABC 和菱形 BFGC 组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°.将其沿 AB，BC 折起使得BE 与BF 重合，连结DG，如图2.

（1）证明：图 2 中的 A，C，G，D 四点共面，且平面ABC⊥平面BCGE；

（2）求图2 中的二面角B-CGA 的大小.

微专题复习课的任务就是抓住重点、突破难点、澄清疑点、重视“四基”、培养“四能”，在适当的版块增设微专题，以一条明显的逻辑主线串联起相关的知识、题目、方法，帮助学生构建清晰的知识体系，把握一类问题的本质和通法，起到见微知著的效果。通过微专题的学习，不仅能使学生快速掌握解题的宝典，更是促进了教师对某一具体问题的深入研究，有利于专业的发展。